A Note on Generalized Long Modules

(1.School of Mathematics and Statistics,Guizhou University of Finance and Economics, Guiyang,550025)

(2.College of Mathematics and Information Science,Henan Normal University,Xinxiang, Henan,453007)

A Note on Generalized Long Modules

GUO SHUANG-JIAN1AND DONG LI-HONG2

(1.School of Mathematics and Statistics,Guizhou University of Finance and Economics, Guiyang,550025)

(2.College of Mathematics and Information Science,Henan Normal University,Xinxiang, Henan,453007)

Communicated by Du Xian-kun

LetHLBbe the category of generalized Long modules,that is,H-modules and B-comodules over Hopf algebras B and H.We describe a new Turaev braided group category over generalized Long moduleHLB(S(π))where the opposite group S(π)of the semidirect product of the opposite group πopof a group π by π.As an application,we show that this is a Turaev braided group-categoryHLBfor a quasitriangular Turaev group-coalgebra H and a coquasitriangular Turaev group-algebra B.

Turaev braided group category,generalized Long module,Turaev group-(co)algebra,(co)quasitriangular structure

1 Introduction

For a group π,Turaev[1]introduced the notion of a braided π-monoidal category,here called Turaev braided π-category,and showed that such a category gives rise to a 3-dimensional homotopy quantum fi eld theory.Kirillov[2]found that such Turaev braided π-categories also provide a suitable mathematical tool to describe the orbifold models which arise in the study of conformal fi eld theories.Virelizier[3]used Turaev braided π-category to construct Hennings-type invariants of fl at π-bundles over complements of links in the 3-sphere.We note that a Turaev braided π-category is a braided monoidal category when π is trivial.

Starting from the category of Yetter-Drinfeld modules,Panaite and Staic[4]constructeda Turaev braided category over certain group,generalizing the work of Staic[5].Some recent related works can be found in[6–8].

The paper is organized as follows.In Section 2,we show that the braided monoidal structure on the categoryHLBdepends on additional compatibility conditions(see Theorem 2.3).In Section 3,we fi nd thatHLB(S(π))is a Turaev braided S(π)-category if and only if there is a linear map Q:B⊗B−→H⊗H satisfying some conditions(see Theorem 3.8).In Section 4,as an application,for a quasitriangular Turaev S(π)-coalgebra H and a coquasitriangular Turaev S(π)-algebra B,we show thatHLB(S(π))is a Turaev braided S(π)-category(see Theorem 4.4).

2 Preliminaries

Throughout the paper,let k be a fi xed fi eld and⊗be over k.For a Hopf algebra H,we always denote by Aut(H)the group of Hopf automorphism of H.For the comultiplicationΔin a coalgebra C,we use the Sweedler-Heyneman’s notation(see[9]):

We denote by ModBthe category of the right B-comodules and for any M ∈ModB,we write

Similarly,we have theHMod of left H-modules.

De fi nition 2.1[1]Letπbe a group with the unite.Recall from[1]that a Turaevπ-category is a monoidal categoryCwhich consists of the following data:

(1)A family of subcategoriessuch thatCis a disjoint union of this family and such thatU⊗V∈Cαβ,for anyα,β∈π,if theU∈CαandV∈Cβ.Here the subcategoryCαis called theαth component ofC;

(2)A group homomorphismφ:π−→aut(C),βφβ,the conjugation,(whereaut(C)is the group of invertible strict tensor functors fromCto itself)such thatφβ(Cα)=Cβαβ−1for anyα,β∈π.Here the functorsφβare called conjugation isomorphisms.

We use the left index notation(see[8,10]):Givenβ∈Gand an objectV∈Cβ,the functorφβwill be denoted byV(·)orβ(·).We use the notationforβ−1(·).Then we haveVidU=idVUandV(g◦f)=Vg◦Vf.We remark that since the conjugationφ:π−→aut(C)is a group homomorphism,for anyV,W∈C,we have

and that since,for anyV∈C,the functorV(·)is strict,we haveV(f⊗g)=Vf⊗Vg,for any morphismfandginC,andV1=1.And we useC(U,V)to denote a set of morphisms(or arrows)fromUtoVinC.

A Turaev braidedπ-category is a Turaevπ-categoryCendowed with a braiding,i.e.,with a family of isomorphismssatisfying the following conditions:

(1)for any arrowf∈Cα(U,U′)withα∈G,g∈C(V,V′),we have

(2)for allU,V,W ∈C,we have

(3)for anyU,V∈C,α∈π,

De fi nition 2.2[11]LetGandLbe two groups andGact on the left the groupLby automorphisms.ThenL×Gis a group with the multiplication

which is called a semi-direct product ofLbyGand denoted byLG.A groupπis a semidirect product ofLbyGif and only ifLis a normal subgroup ofπ,Gis a subgroup ofπ, L∩G=1,andπ=LG.

Letπbe a group and letL=πop,the opposite group of a groupπ.Consider the adjoint action ofπonLby de fi ning:γ▷α=γαγ−1for allα,γ∈π.Then we have the semi-direct productπopπ.The opposite group(πopπ)opof the groupπopπis denoted byS(π)with the multiplication,for allα,β,λ,γ∈π:

which is called a twisted semi-direct square of groupπ.Moreoverπis a subgroup ofS(π)and(α,β)−1=(β−1α−1β,β−1).

3 Generalized Long Module Categories

In this section we fi rst introduce the notion of a generalized Long module,generalizing the one named dimodule in[5],and show that the categoryHLBof generalized Long modules is symmetric.

De fi nition 3.1LetBandHbe Hopf algebras.Then a left-right generalized Long module is a triple(M,·,ρ)such that(M,·)is an object inHModand(M,ρ)inModBand satis fi es the following compatibility condition:

Let M and N be two left generalized Long modules.A morphism from M to N means both a left H-module map and a right B-comodule map.A left-right generalized Long module categoryHLBconsists of left generalized Long modules and their morphism.

Proposition 3.1LetBandHbe Hopf algebras.Then the categoryHLBof left-right generalized Long modules is a monoidal category with the following structure:

h·(m⊗n)=(h2·m)⊗(h1·n),

ρ(m⊗n)=m(0)⊗n(0)⊗n(1)m(1), h∈H,m∈M∈HLB,n∈N∈HLB.

Generally,the categoryHLBis not a braided monoidal category.However,the proof of the following result is straightforward.

Theorem 3.1Let(H,R)be quasitriangular and(B,σ)be coquasitriangular.The categoryHLBis a braided monoidal category.The braiding onHLB:

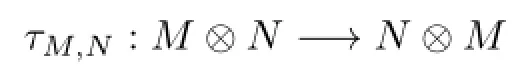
is given by

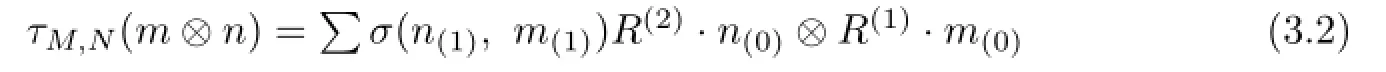
for allM,N∈HLB,m∈Mandn∈N.Moreover,if(H,R)is triangular and(B,σ)is cotriangular,thenHLBis symmetric.

Example 3.1(1)Let J be any commutative and cocommutative Hopf algebra.Then J has the trivial triangular structure R=1⊗1 and the trivial cotriangular structure〈x|y〉=ε(x)ε(y)for all x,y∈J,and the categoryJLJof J-dimodules is a left generalized Long module category and a symmetric category.

(2)Let Z2be the cyclic group of order 2 with the basis{1,g}.Then one has that (H=kZ2,R)is the triangular Hopf algebra with R=1 2(1⊗1+1⊗g+g⊗1+g⊗g). If we take B=H∗,then it is well-known that(B,σ)is the cotriangular Hopf algebra with the basis{1,G}and with the cotriangular structure σ(1,G)=1=σ(1,1)=σ(G,1); σ(G,G)=−1.ThenHLBis a generalized Long module category.

(3)Let(H,R)be a triangular Hopf algebra and B a commutative Hopf algebra.Then the categoryHMod is a symmetric subcategory ofHLBwith the trivial B-comodule structure, i.e.,ρ(m)=m⊗1 for all m∈M ∈HLBand the braiding de fi ned as∑

for all M,N∈HMod,m∈M and n∈N.

(4)Let(B,〈·|·〉)be a cotriangular Hopf algebra and H a cocommutative Hopf algebra.Then the category ModBis a symmetric subcategory ofHLBwith the trivial module structure,i.e.,h·m=ε(h)m for all h∈H,m∈M∈HLBand the braiding given by

for all M,N∈ModB,m∈M and n∈N.

4 A Turaev Braided S(π)-categoryHLB(S(π))

In this section,we mainly consider the Turaev S(π)-categoryHLB(S(π)).Let B and H be Hopf algebras,π be a any group with the unit e,and S(π)be the twisted semi-direct square group of π.Let ξ:π−→Aut(H)and ζ:π−→Aut(B)be group homomorphisms.

Proposition 4.1LetM∈HLB((α,β))andN∈HLB((γ,δ)).Then we haveM⊗N∈HLB(((α,β)#(γ,δ)))with structures:

Proof.It is easy to check that M⊗N is a left H-module and M⊗N is a right B-comodule. The following is a check that the compatibility condition holds:

which shows that M⊗N∈HLB((α,β)#(γ,δ)).

Proposition 4.2LetN ∈HLB((γ,δ))and(α,β)∈S(π).De fi ne(α,β)N=Nas a vector space with the structures

Then we have

Furthermore,letM∈HLB((α,β))and(µ,ν)∈S(π).Then we have

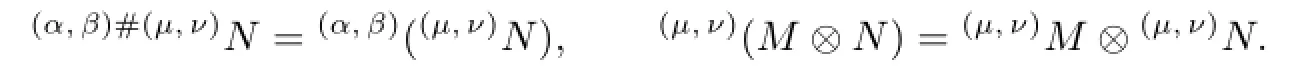
De fi ne a group homomorphism φ:S(π)−→Aut(HLB(S(π))),(α,β)φ(α,β),as

and the functor φ(α,β)acts as identity on morphisms.Now,we consider a map

with a twisted convolution inverse R,which means that

for all c,d∈B.Sometimes,we write Q(c⊗d):=Q1(c⊗d)⊗Q2(c⊗d)for all c,d∈B.

Let M∈HLB((α,β)),N∈HLB((γ,δ)),and P∈HLB((µ,ν)).De fi ne a map as

In what follows,our main aim is to fi nd some necessary and sufficient conditions on Q such that the cM,Nde fi nes a braiding onHLB(S(π)).For this,we fi nd conditions under which cM,Nis both H-linear and B-colinear,and the following conditions hold:

Furthermore,if M∈HLB((α,β))and N∈HLB((γ,δ)),then we want to show that

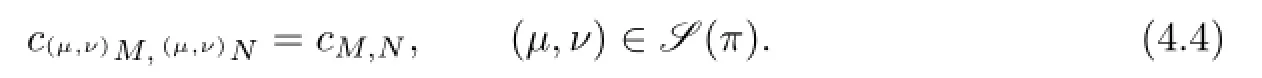
In order to approach to our main result we need some lemmas.

Lemma 4.1LetM∈HLB((α,β))andN∈HLB((γ,δ)).ThencM,NisH-linear if and only if the following condition is satis fi ed:

Proof.If cM,Nis H-linear,then it is easy to get

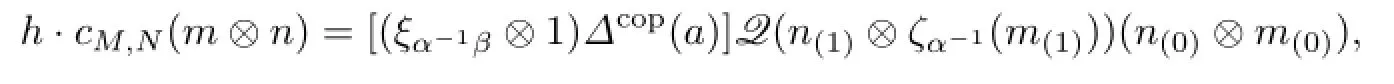
and

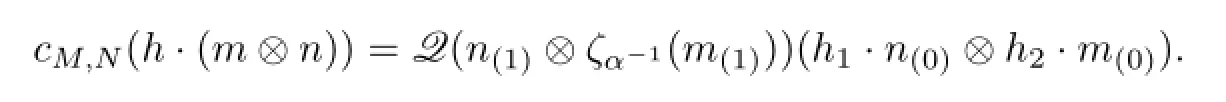
Considering these equations and taking M=N=H⊗B and m=1⊗c and n=1⊗d for all c,d∈B,we can get(4.5).Conversely,by the above formulas it is easy to see that cM,Nis H-linear.

Lemma 4.2LetM ∈HLB((α,β))andN∈HLB((γ,δ)).ThencM,NisB-colinear if and only if the following condition is satis fi ed:

Proof.If cM,Nis B-colinear,then we do the following calculation:

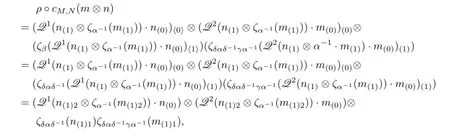
and

Now,we let M=N=H⊗B and take m=1⊗c and n=1⊗d for all c,d∈B.Then we can get(4.6).Conversely,by the above formulas it is easy to see that cM,Nis B-colinear.

Lemma 4.3LetM ∈HLB((α,β)),N∈HLB((γ,δ))andP∈HLB((µ,ν)).Then(4.2)holds if and only if the following condition is satis fi ed withU=Q:

Proof.If(4.2)holds,then we compute as follows:

and

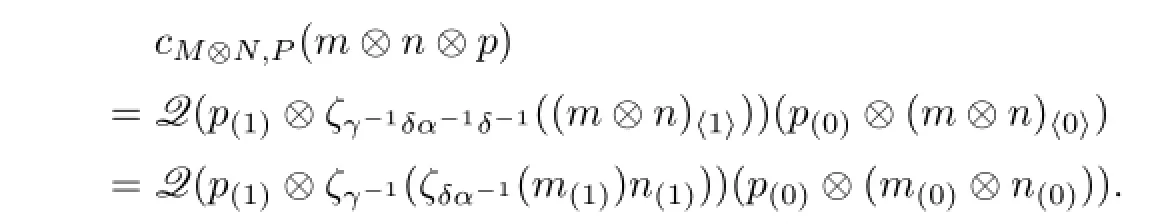
Take M=N=P=H⊗B,m=1⊗c,n=1⊗d,and p=1⊗f for all c,d,f∈B.Then we obtain(4.7).Conversely,the proof is straightforward.We omit the details.

Lemma 4.4LetM ∈HLB((α,β)),N∈HLB((γ,δ))andP∈HLB((µ,ν)).Then(4.3)holds if and only if the following condition is satis fi ed withU=Q:

Proof.If(4.3)holds,then we have

and

Take M=N=P=H⊗B,m=1⊗c,n=1⊗d,and p=1⊗f for all c,d,f∈B.Then we obtain(4.8).Conversely,it is straightforward.

Lemma 4.5LetM∈HLB((α,β))andN∈ALB((γ,δ)),and(µ,ν)∈S(π).Then(4.4)holds if and only if the following condition holds:

Proof.If(4.4)holds,i.e.,we have cµ,νM,µ,νN=cM,N,then

Take M=N=H⊗B,m=1⊗c,and n=1⊗d.Then we obtain(4.9).Conversely,it is obvious.

Therefore,we can summarize our results as follows.

Theorem 4.1LetHandBbe bialgebras andπbe a group with the unit1.Letξ:π−→Aut(H)andζ:π−→Aut(B)be group homomorphisms,andQ:B⊗B−→H⊗Hbe a twisted convolution invertible map.Then the family of maps given by(4.1)de fi nes a braiding inHLB(S(π))and make it a Turaev braidedS(π)-category if and only if(4.5)–(4.9)are satis fi ed.

5 Applications

In this section we give two applications of our theory to the following cases:

(I)B=H and H is a commutative and cocommutative Hopf algebra;

Theorem 5.1(Case I)The categoryHLHHYDHas the Turaev braidedS(π)-category for a commutative and cocommutative Hopf algebraH.The braiding is given by

Proof.De fi ne a map Q:H⊗H→H⊗H given by Q(h⊗g)=g⊗εH(h)1 for all h,g∈H. De fi ne now a map R:H⊗H → H⊗H given by R(h⊗g)=S−1(g)⊗εH(h)1 for all h,g∈H.Then R is the inverse of Q.

Next,we show another application of our theory(Case II).

De fi nition 5.1Letξ:π−→ Aut(H)be a group homomorphism.A quasitriangular Turarvπ-coalgebra is a pair(H,),whereHis a Hopf algebra and

is a convolution invertible element with an invertible elementR−1such that the following conditions hold

De fi nition 5.2Letζ:π−→ Aut(B)be a group homomorphism.A coquasitriangular Turaevπ-algebra is a pair(B,σ),whereBis a Hopf algebra andσ:B⊗B→kis a linear form(braiding)which is convolution invertible inHomk(B⊗B,k)such that the following conditions hold:

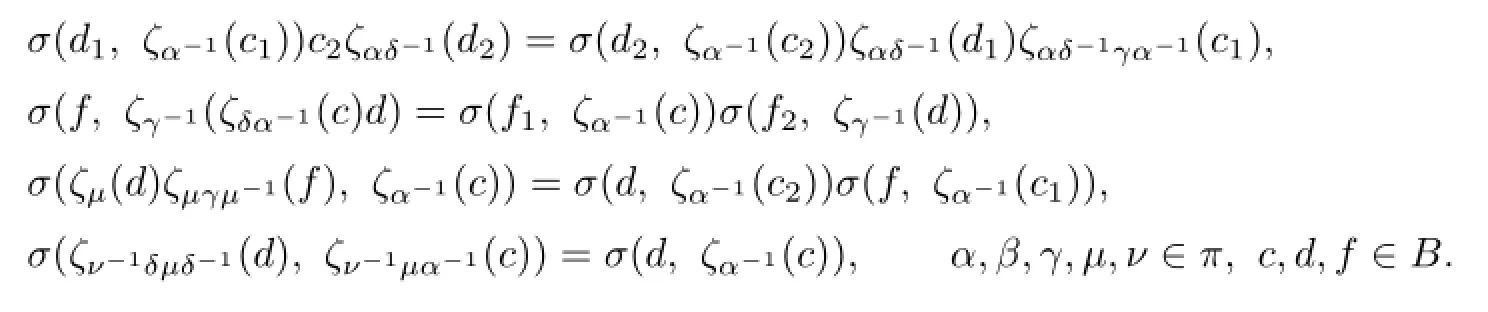
Theorem 5.2(Case II)Let(H,)be a quasitriangular Turaevπ-coalgebra and(B,σ)a coquasitriangular Turaevπ-algebra.Letξ:π−→ Aut(H)andζ:π−→ Aut(B)be two group homomorphisms.Then the categoryHLB(S(π))is a Turaev braidedS(π)-category with the following structures:

(1)LetM∈HLB((α,β)),N∈HLB((γ,δ)).ThenM⊗N∈HLB(((α,β)#(γ,δ)))with the following monoidal structures:

andkis the unit ofHLB;

(2)LetN∈HLB((γ,δ))and(α,β)∈S(π).Then(α,β)Nhas the following structures:

(3)LetM∈HLB((α,β)),N∈HLB((γ,δ)).The braiding is given by

Corollary 5.1Let(H,˜R)be a quasitriangular Hopf algebra andξ:π−→Aut(H)be a group homomorphism.Then the categoryHModis a Turaev braidedS(π)-subcategory ofHLB(S(π)),and the braiding is given by

Corollary 5.2Let(B,σ)be a coquasitriangular Hopf algebra andζ:π−→Aut(B)be a group homomorphism.Then the categoryModBis a Turaev braidedS(π)-subcategory ofHLB(S(π)),and the braiding is given by

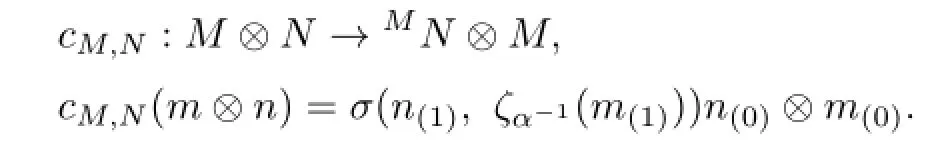
[1]Turaev V.Crossed group-categories.Arabian J.Sci.Engrg.,2008,33C:483–503.

[2]Kirillov A J.On G-equivariant modular categories.arXiv:math/0401119v1[math.QA].submitted on 12 Jan.2004.

[3]Virelizier A.Involutory Hopf group-coalgebras and fl at bundles over 3-manifolds.Fund.Math., 2005,188:241–270.

[4]Panaite F,Staic M D.Generalized(anti)Yetter-Drinfel’d modules as components of a braided T-category.Israel J.Math.,2007,158:349–366.

[5]Staic M D.A note on anti-Yetter-Drinfeld modules.Contemp.Math.,2007,441:149–153.

[6]Caenepeel S,De Lombaerde M.A categorical approach to Turaev’s Hopf group-coalgebras. Comm.Algebra,2006,34(7):2631–2657.

[7]Wang S H.New Turaev braided group categories and group Schur-Weyl duality.Appl.Categ. Structures,2013,21(2):141–166.

[8]Zunino M.Yetter-Drinfeld modules for crossed structures.J.Pure Appl.Algebra,2004,193: 313–343.

[9]Sweedler M.Hopf Algebras.New York:Benjamin,1969.

[10]Virelizier A.Hopf group-coalgebras.J.Pure Appl.Algebra,2002,171:75–122.

[11]Wang S H.Tuaev group coalgebras and twisted Drinfeld double.Indiana Univ.Math.J.,2009,58:1395–1417.

tion:16W30

A

1674-5647(2014)04-0320-09

10.13447/j.1674-5647.2014.04.05

Received date:April 18,2012.

Foundation item:The NSF(11101128)of China,the NSF(102300410049)of Henan Province and the NSF (BK2012736)of Jiangsu Province.

E-mail address:shuangjguo@gmail.com(Guo S J).