A Note on the Connectedness of the Invertible Group of a Nest Algebra

(School of Mathematics,Jilin University,Changchun,130012)

A Note on the Connectedness of the Invertible Group of a Nest Algebra

ZHANG MIN AND YUE HUA

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Ji You-qing

The connectedness of the invertibles question for arbitrary nest has been reduced to the case of the lower triangular operators with respect to a fi xed orthonormal basis enfor n≥ 1.For each f∈H∞,let Tfbe the Toeplitz operator.In this paper we prove that Tfcan be connected to the identity through a path in the invertible group of the lower triangular operators if f satis fi es certain conditions.

connectedness,nest algebra,invertible group

1 Introduction

A well-known problem in operator theory is whether the group of invertible operators in a nest algebra is connected in the norm topology.David Larson remembered people in system theory raising it in late 1970s.William Arveson promoted this problem for many years,in particular,discussed it at a meeting in Berkeley in 1981 in honour of Paul Halmos.Davidson also raised this problem as one of the ten important problems in that area in a talk at the 1987 GPOTS meeting in Kansas(see[1]and Chapter 25 in[2]).In spite of all this,there has been no signi fi cant progress until the emergence of the deep interpolation theorem of Orr[3].In 1993,Davidson and Orr[4]achieved a breakthrough in solving the connectedness problem.By using the interpolation theorem of Orr,they showed that the invertibles are connected in each nest algebra of in fi nite multiplicity.This is the fi rst signi fi cant progress about the connectedness problem.And soon after,in 1994,Davidson,Orr and Pitts[5]successfully extended these results by showing that the invertibles are connected in a nest algebra provided there is a fi nite bound on the number of consecutive fi nite rank atoms inthe nest.Their work reduced the connectedness of the invertibles question for arbitrary nests to the case of the lower triangular operators with respect to a fi xed orthonormal basis enfor n≥1.

Let T be the unit circle in the complex plane with normalized Lesbegue measure.For 1≤p≤∞,let Hpbe the usual Hardy space of all functions in Lp(T)which have analytic extensions to the open unit disk D.Let H=H2(T)and B(H)be the set of all bounded linear operators on H,and W ∈B(H)be the shift operator with(Wf)(eiθ)=eiθf(eiθ).In this paper we consider the nest N={{0},WnH:n∈Z,n≥0}of subspaces of H and its associated nest algebra

Is the group of invertible elements of Banach algebra AlgN connected in the norm topology?It is frequently conjectured that the answer to this question is“no”.The reason for conjecturing a negative answer is due to a strong analogy between nest algebras and analytic function theory.Pitts[6]proposed a function f which cannot be connected to the constant function 1 via a norm continuous path within the group of invertible elements of the Banach algebra H∞,however the Toeplitz operator with symbol f can be connected to the identity via a norm continuous path of invertible elements in AlgN.Inspired by Pitts[6]we show that a certain class of invertible elements in AlgN can be connected to the identity in norm topology in this paper.

The main results are the theorems as follows.

Theorem 1.1IfT∈AlgNis invertible andσ(T)consists of fi nite points,thenTcan be connected to the identity through a path in the invertible group ofAlgN.

Theorem 1.2Lethbe an analytic function in the open unit discDwith the bounded real part and(n)be then-th Fourier coefficient ofh.If there exists a natural numberksuch that(kl)=0for eachl∈Z,then the Toeplitz operatorTfwith symbolfcan be connected to the identity through a path in the invertible group ofAlgN,wheref=eh.

2 Proofs of Theorems

Proof of Theorem 1.1Since σ(T)consists of fi nite points,we assume that

For each i,1≤i≤k,we can fi nd an open neighborhoodΩiof λisuch that

are pairwise disjoint.Set

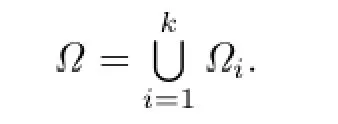
For each i,1≤i≤k,de fi ne

Then each fiis an analytic function on the open neighborhoodΩof σ(T).So fi(T)(1≤i≤k)is well de fi ned.Denote

By the Riesz Dunford functional calculus,each Piis an idempotent,that is,P2i=Pi, and moreover,

So T admits the matrix representation as follows:

where σ(Ti)={λi}for 1≤i≤k.

Claim 2.1Pi∈AlgN for each 1≤i≤k.

Since pn(T)∈AlgN for all n,we conclude that

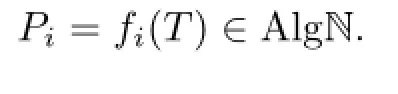
This proves the claim.

For each i,noticing that σ(Ti)={λi},we assume that Ti= λi+qi,where qiis a quasinilpotent operator on Mi.Thus

Since Pi∈AlgN,let

Then Qi∈AlgN for each i.Let

The path

lies in AlgN.Thus T can be connected to the operator A.

Since λi≠0 for all i and each Pilies in AlgN,one can see that A is connected to the identity through a path of invertible operators in AlgN.

Proof of Theorem 1.2For a fi xed natural number k,Sqis the unitary operator mentioned above.Let

After a simple calculation,we have that

Multiply both sides of the equations respectively and let

Then

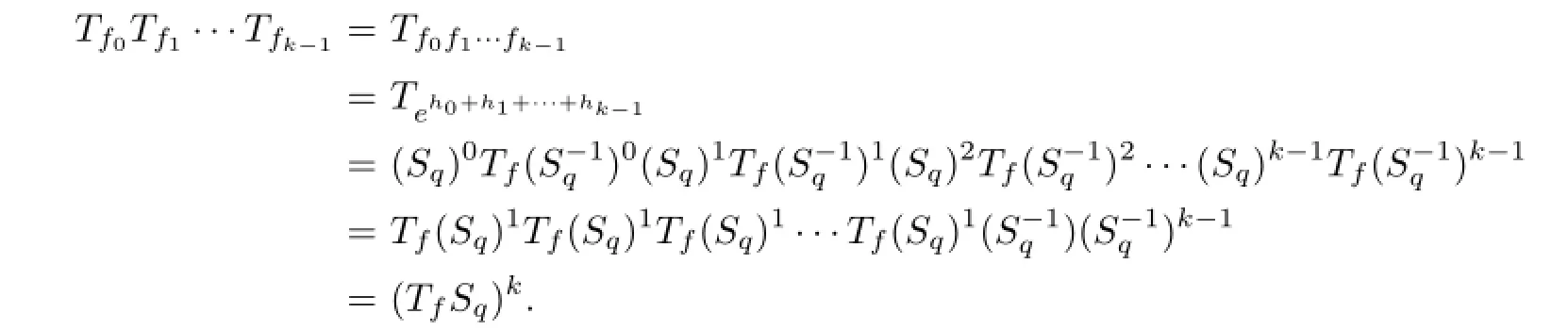
We have

Then we have(TfSq)k=I.By the spectral mapping theorem,both σ(TfSq)and σ(Sq) consist of fi nite points.Then by Theorem 1.1,Sqand TfSqare connected to the identity through a path in the invertible group of AlgN.So is Tf.

[1]Davidson K R.Problems about re fl exive algebras.Proceedings of the Seventh Great Plains Operator Theory Seminar.Lawrence,KS,1987.Rocky Mountain J.Math.,1990,20(2):317–330.

[2]Davidson K R.Nest Algebras.Triangular forms for operator algebras on Hilbert space.Pitman Research Notes in Mathematics Series 191.Harlow:Longman Scienti fi c Technical,1988.

[3]Orr J L.Triangular algebras and ideals of nest algebras.Bull.Amer.Math.Soc.,1990,23(2): 461–467.

[4]Davidson K R,Orr J L.The invertibles are connected in in fi nite multiplicity nest algebras.Bull. London Math.Soc.,1995,27(2):155–161.

[5]Davidson K R,Orr J L,Pitts D R.Connectedness of the invertibles in certain nest algebras. Canad.Math.Bull.,1995,38(4):412–420.

[6]Pitts D R.A note on the connectedness problem for nest algebras.Proc.Amer.Math.Soc., 1992,114(1):181–183.

tion:47D25,46K50

A

1674-5647(2014)04-0329-05

10.13447/j.1674-5647.2014.04.06

Received date:March 13,2012.

Foundation item:The NSF(10971079)of China and the Basic Research Foundation(201001001,201103194) of Jilin University.

E-mail address:zmin@jlu.edu.cn(Zhang M).