The Maximum Trigonometric Degrees of Quadrature Formulae with Prescribed Nodes

LUO ZHONG-XUAN,2,YU RANAND MENG ZHAO-LIANG

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024)

(2.School of Software Technology,Dalian University of Technology,Dalian,Liaoning,116620)

The Maximum Trigonometric Degrees of Quadrature Formulae with Prescribed Nodes

LUO ZHONG-XUAN1,2,YU RAN1AND MENG ZHAO-LIANG1

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024)

(2.School of Software Technology,Dalian University of Technology,Dalian,Liaoning,116620)

Communicated by Ma Fu-ming

The purpose of this paper is to study the maximum trigonometric degree of the quadrature formula associated with m prescribed nodes and n unknown additional nodes in the interval(−π,π].We show that for a fi xed n,the quadrature formulae with m and m+1 prescribed nodes share the same maximum degree if m is odd.We also give necessary and sufficient conditions for all the additional nodes to be real,pairwise distinct and in the interval(−π,π]for even m,which can be obtained constructively.Some numerical examples are given by choosing the prescribed nodes to be the zeros of Chebyshev polynomials of the second kind or randomly for m≥3.

quadrature formula,trigonometric function,bi-orthogonality,truncated complex moment problem

1 Introduction

Let ω(θ)be a non-negative weight function on(−π,π],vanishing there only on a set of a measure zero.For the integration of the form

a quadrature formula

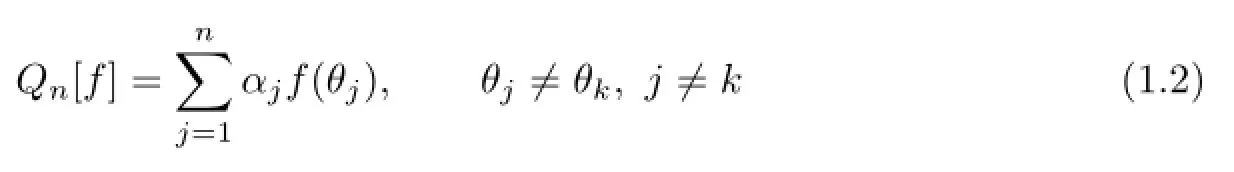
is said to have trigonometric degree d if Qn[f]=I[f]for any f∈and for at least one g∈such that Qn[g]≠I[g],where

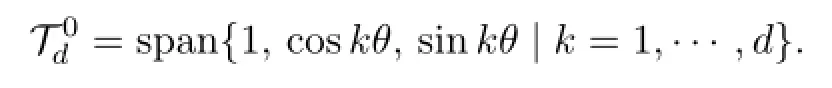
Typically,θjand αjare called nodes and weights of Qn[f],respectively.

Recently,the following problem has been arisen:

Problem 1.1Given m distinct points⊂(−π,π]and n∈N, fi nd n distinct points⊂(−π,π]and positive numberssuch that the quadrature formula

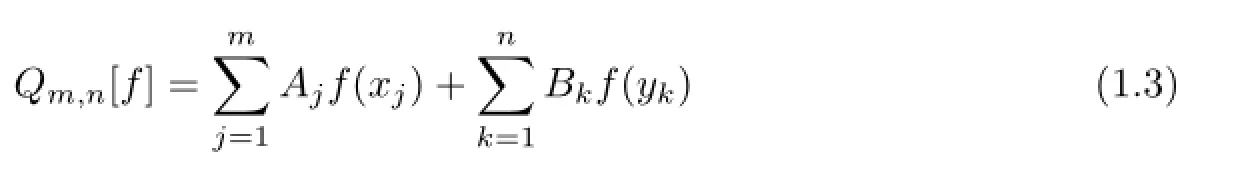
has maximum trigonometric degree.

Problem 1.1 has been dealt with when m=1 and m=2 by Jagels and Reichel[1]and Butheelet al.[2],using the technique of complex analysis.These formulae are called the Szeg¨o-Radau(m=1)and Szeg¨o-Lobatto(m=2)quadrature formulae,respectively.

In this paper,we mainly study the maximum trigonometric degree of(1.3)for any positive integer m.The maximum degree is denoted by dmax(m,n)and given in Theorem 2.1.Some simple computation shows that for a fi xed n,the quadrature formulae with m and m+1 prescribed nodes share the same degree when m is odd.Furthermore,for even m, with the theory of Complex K-Moment Problem(CMP)(see[3–9]and references therein), we obtain necessary and sufficient conditions of the existence of ykhaving the property that they are real,pairwise distinct and in the interval(−π,π].If such conditions are satis fi ed,the nodes ykand all the weights can be computed constructively.To facilitate the description,the nodes satisfying the above property are called simple nodes and the quadrature formulae of the form(1.3)with simple nodes ykand positive weights Aj,Bkare called desired quadrature formulae.

The paper is organized as follows.The maximum trigonometric degree of(1.3)is studied in Section 2 for any positive integer.The necessary and sufficient conditions of the existence of simple additional nodes are discussed in Section 3.Some examples are shown in Section 4.A brief conclusion is given in Section 5.

2 Maximum Trigonometric Degrees

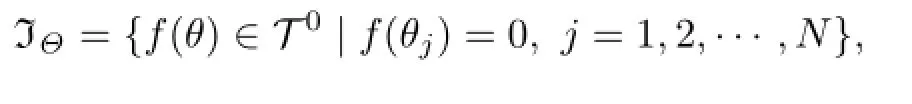
and

Let N0=dimThe construction of(1.3)is related to the spaces

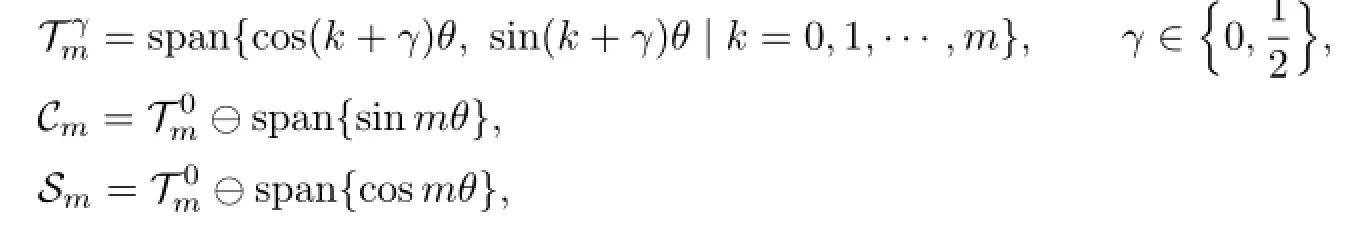
and the following lemma.

Lemma 2.1The following statements are equivalent:

(1)f(θ)∈IΘ∩⇒I[f]=0;

(2)There exists a quadrature formula

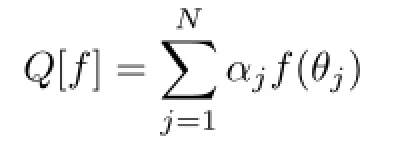
such thatI[f]=Q[f]for anyf∈with at mostN0non-zero weightsαj.

Proof.Since IΘ∩T0d⊂T0d,(2)⇒(1)is obvious.Now we prove(1)⇒(2).Let

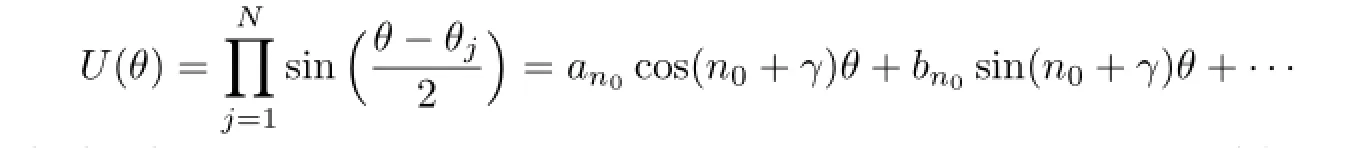
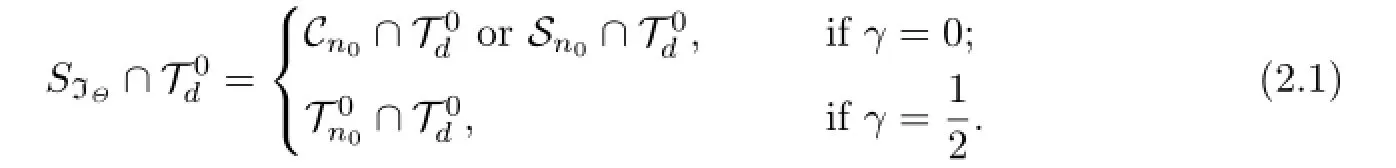
Then N0=dim(SIΘ∩T0d)≤ N.Setting γ=0,we see that there exists a quadrature formula Q[f]such that

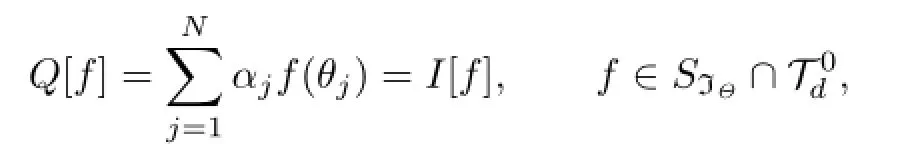
where at most N0weights αjare not zero.Let T(θ)∈Then there exists a YN(θ)∈SIΘ∩such that

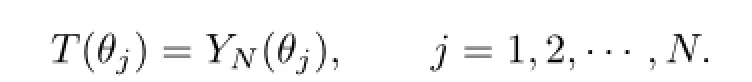
Thus(T−YN)(θj)=0,j=1,2,···,N,which implies that T(θ)−YN(θ)∈IΘ∩that is,there exists a W(θ)∈IΘ∩such that

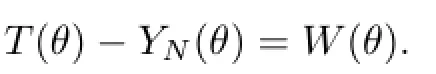
i.e.,T(θ)=YN(θ)+W(θ).Then

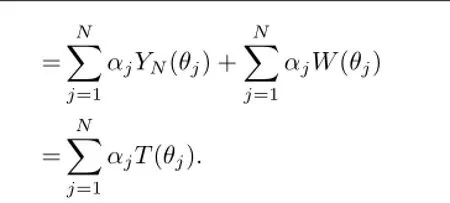
Now,we present the result about the maximum trigonometric degree of(1.3).

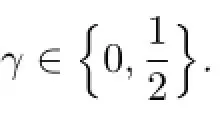
where[x]denotes the integer part ofx.The additional nodesare the zeros of the trigonometric function which is orthogonal to all the functions inFurthermore,ifmis odd,then

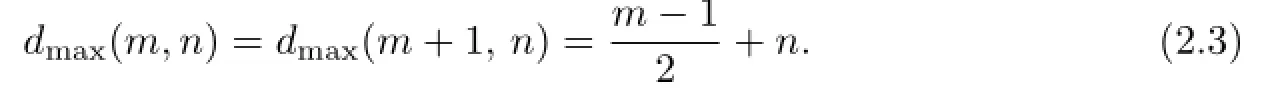
Proof.Let

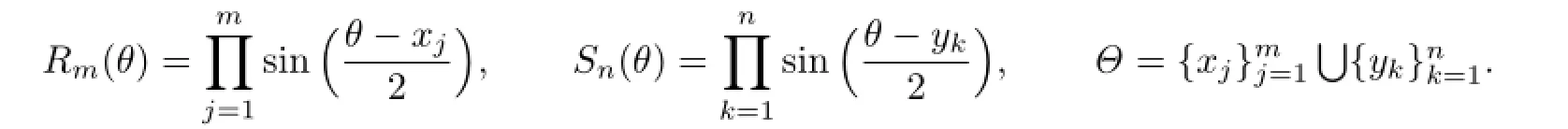
By Lemma 2.1,there exists a quadrature formula of degree d if the following statement holds:

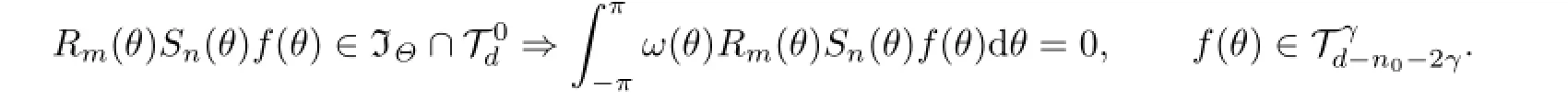
Hence,the construction of(1.3)depends on the construction of Sn(θ)with

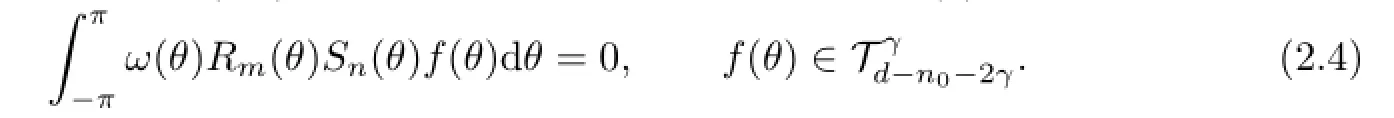
There are n unknowns on the left side of(2.4),i.e.,And the dimension ofis τ=2(d−n0−2γ)+1+2γ.We set τ=n if τ and n are of the same parity,or τ=n−1 if they are of opposite parity.Thus,we obtain

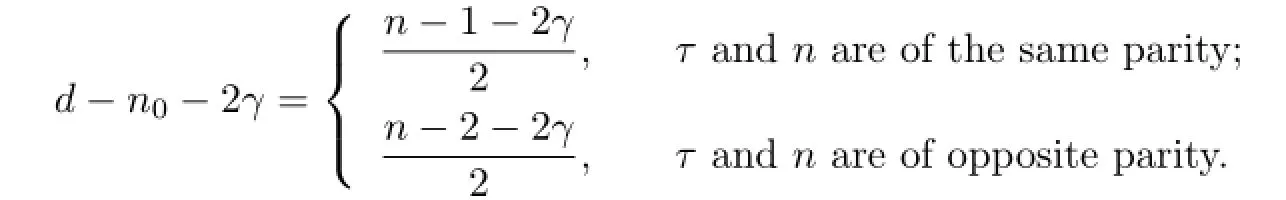
By further computation for dmax(m,n),we obtain

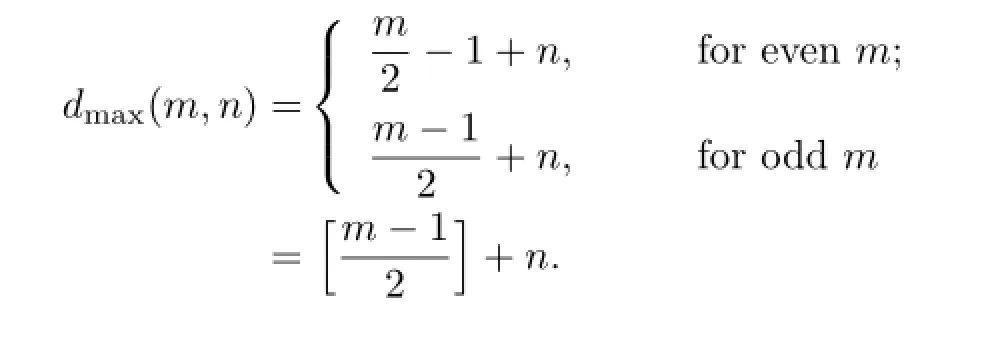
Then for an odd number m,dmax(m,n)and dmax(m+1,n)are the same which can be written as(2.3)uniformly.The proof is completed.

From above we obtain dmax(m,n)=n for m=1,2,which coincides with the results in [1–2].We also note that if m=0,then dmax(0,n)=n−1,which is the classical result about the quadrature formulae of trigonometric degree(see[10–12],for example).For m≥3,we give some numerical examples in Section 4.

Although the maximum trigonometric degree is given in(2.2)or(2.3),Theorem 2.1 does not guarantee that the additional nodes are simple and all the weights,Ajand Bk,are positive.However,if m is even,the nodes{yk}nk=1can be guaranteed to be simple.

3 Construction of Quadrature Formulae

In this section,we fi rst prove the following theorem.

Theorem 3.1Letmprescribed nodes∈(−π,π]be given.Letmbe even andω(θ)be a non-negative weight fun∫ction on(−π,π].Denote

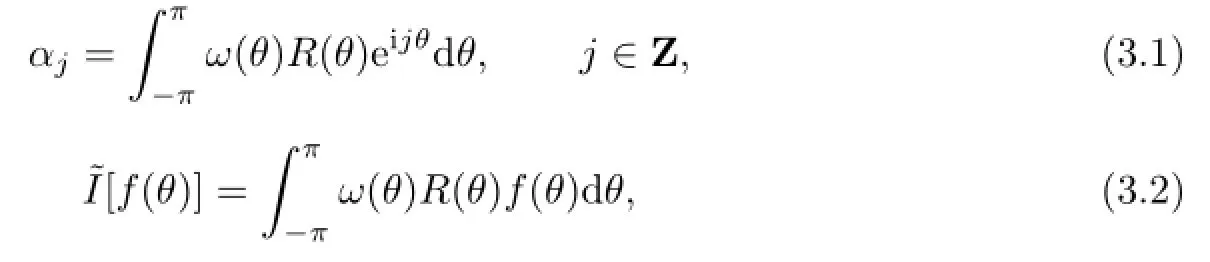
and

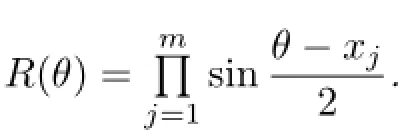
(1)There existnsimple nodesyksuchthatykxj,for eachj,k,and{xj}∪{yk}are the nodes of quadrature formula of degree+n−1in the form(1.3);

(2)There existnsimple nodesyksuch thatR(yk)0and they are the nodes of quadrature formula of degreen−1with respect toI˜[f].

Proof.(1)⇒(2).Assume that the quadrature formula Qm,n[f]in the form(1.3)exists, where the nodes ykare simple.For any function f∈R(θ)f(θ)is a function inThen,we have

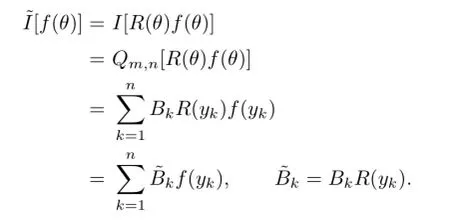
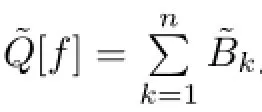
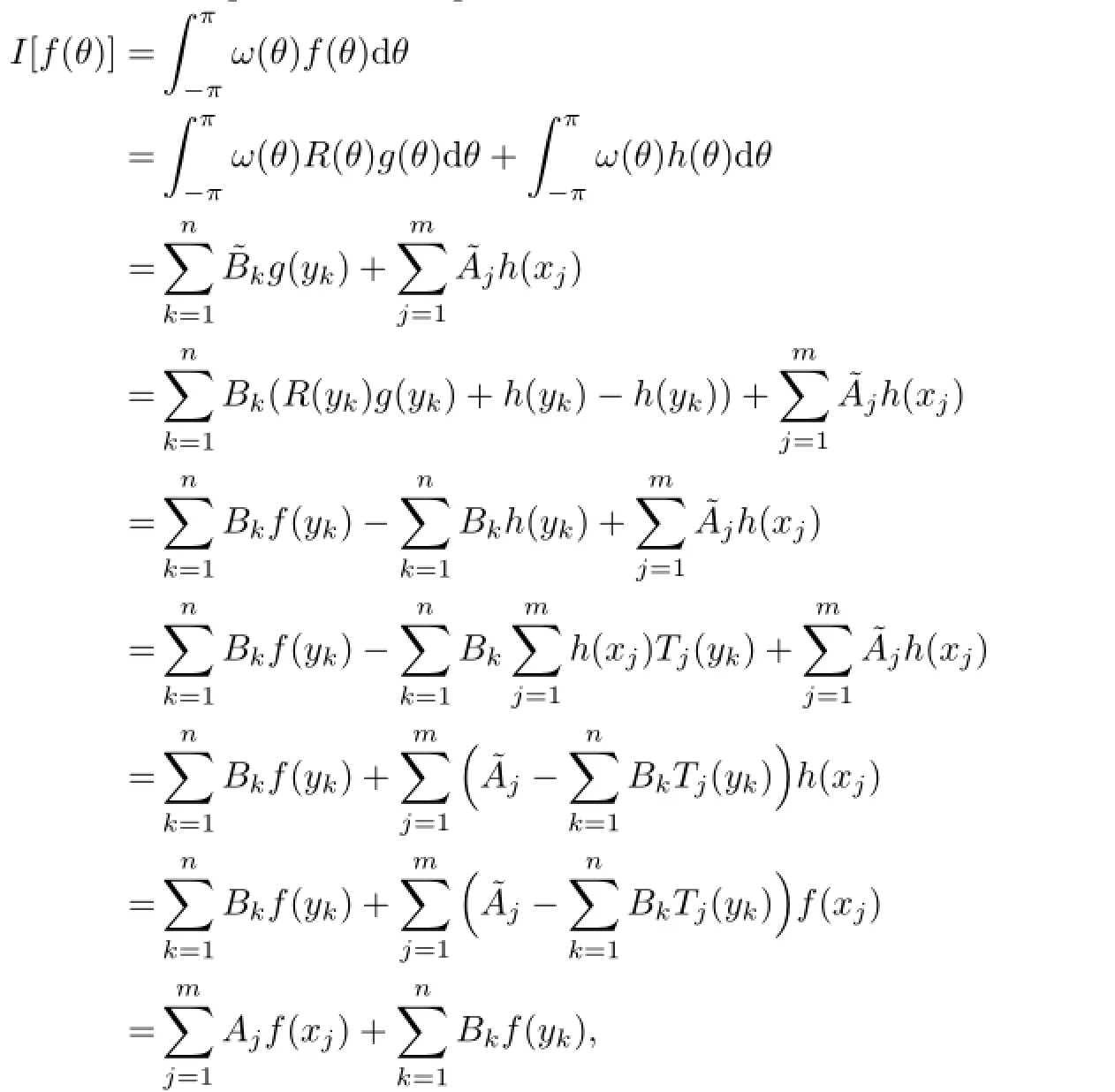
where

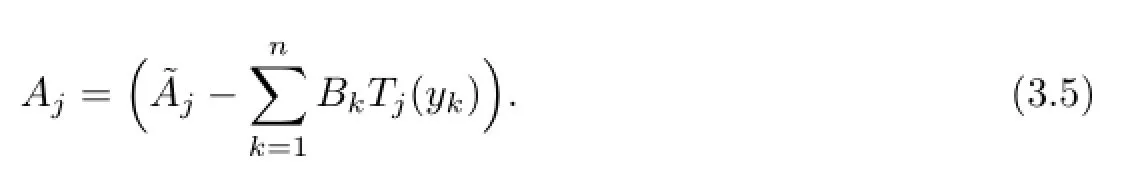
The proof is completed.

Next,we introduce some results about CMP which be used to prove Theorem 3.2.

Given a sequence of complex numbers α={αjk}or α={αj}and a closed subset K∈C, the CMP entails determining if there exists a positive Borel measureµonCsuch that

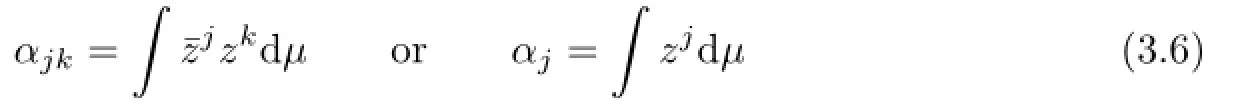
and

If such aµexists,then it is called a representing measure for α.If the sequence α is fi nite, it is also called the Truncated CMP(TCMP).The representing measure is often connected with the Dirac measure.A measureµis said to be r-atomic,if it has fi nite support of the formfor λj̸0,where δvjare Dirac measures and vj∈Care called atoms of µ.More details about the CMP may refer to[3–9]and references therein.

Back to our problem.Let

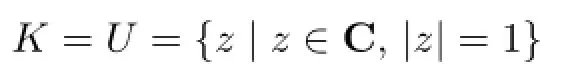
be the unit circle onC.It is well known that the construction of quadrature formula of trigonometric degree d on(−π,π]is equal to the construction of quadrature formula that is exact for the space span{zj|−d≤j≤d}on U(for example,[1–2,10–11]).This relationship is a connection between Problem 1.1 and TCMP.For a given sequence α=let z=eiθ=cosθ+isinθ,i2=−1.The classical truncated trigonometric moment problem is whether there exists a positive Borel measureµsuch that

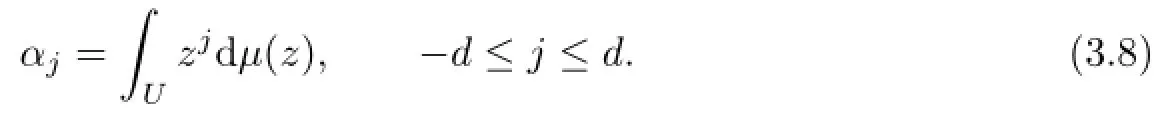
Let Td:=and Di:=|Ti|,the determinate of Ti,i=0,1,···,d.De fi ne the rank of α as

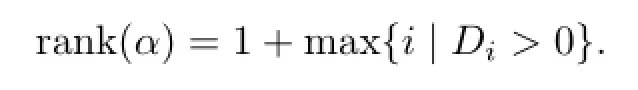
The following lemma gives a necessary and sufficient condition for the sequence α to have a representing measure.

Lemma 3.1[3]Letα=(α−d,···,α0,···,αd)∈C2d+1,α0＞0,α−j=be given.Then there exists a representing measureµforαif and only ifTd≥0.In this case,µcan be chosen to haveratoms,wherer:=rank(α).

In the case that Tdis of full rank,µis(d+1)-atomic.

If we assume that the weights of ykare positive in(2)of Theorem 3.1,then we derive

Theorem 3.2Under the same conditions in Theorem3.1,the following statements are equivalent:

(1)There existnsimple nodesykand positive weightssuch that they are the nodes and weights of quadrature formula of degreen−1with respect to

(2)The Toeplitz matrixTn−1is positive.

Proof.(1)⇒(2).Let

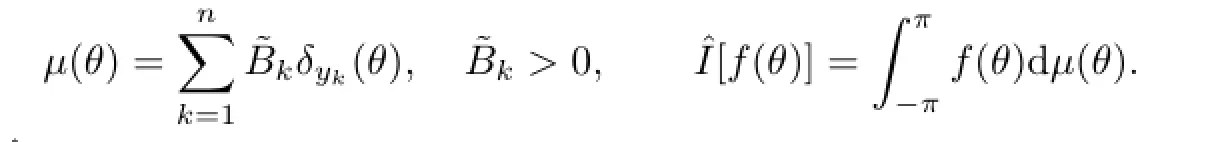
(2)⇒(1).On the contrary,it is obvious by Lemma 3.1.The proof is completed.

If the Toeplitz matrix Tn−1is positive,then the nodes ykcan be characterized by the fl at extension theorem(see[4,6]),bi-orthogonal system(see[10–11])or Szeg¨o polynomials (see[12]).In what follows,we introduce a constructive method in[3]to derive the nodes ykand

Algorithm 3.1Assume that α=(α−(n−1),···,α(n−1))is de fi ned in(3.1)and|Dn−1|0.Then rank(α)=n.

Step 1.Computer Di.If some Di＜0,then α does not admit a representing measure. If Di＞0 for i=0,1,···,n−1,then go to the next step;

Step 2.Let αn=a+bi and α−n=a−bi,a,b∈R.De fi ne

Solve|Tn|=0 in the unknowns a and b;

Step 3.Choose one solution of(a,b)and compute

Step 4.Solve the roots z1,···,znof the following equation

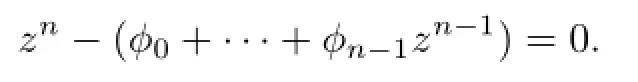
Then ykare the arguments of the complex numbers zk,k=1,···,n;

Step 5.Compute the densities of zkby Vandermonde equation

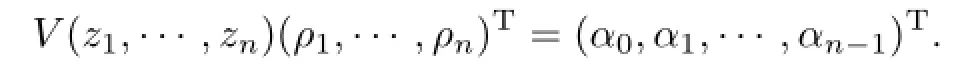
If m is odd,we add one nodes to the setand then use Theorems 3.1 and 3.2 to construct Qm+1,n[f]of degreeFrom(2.3),we see that the degreeis only one less than dmax(m,n+1)=

4 Numerical Examples

In this section,we give some numerical examples by setting ω(θ)=1 for m≥3.First,we construct a quadrature formula by Theorems 3.1 and 3.2.Then,we list several examples, Examples 4.2–4.4,where the additional nodes ykare computed directly by solving the system (2.4).Although Theorem 2.1 does not characterize any other properties about the additional nodes except that they are zeros of Sn(θ)satisfying the system(2.4),a number of examples show that there exist simple nodes and positive weights which solve the Problem 1.1.All the examples are computed in Mathematica 7.0.

Example 4.1m=4,n=7.

The maximum degree dmax(4,7)=8.The prescribed nodes xjare chosen as zeros of Chebyshev polynomials of the second kind of degree 4:

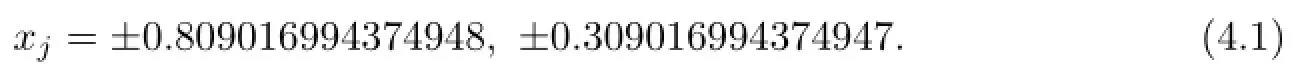
It is easy to compute that T6(α)＞0.Thus by Lemma 3.1 there exists a representing measureµfor α=(αj),where αjis de fi ned by(3.1)for xjin(4.1).Then,by Theorem 3.2, there exist simple nodes yksuch that the quadrature formula Q4,7[f]has degree 8.In the following,we compute ykandby Algorithm 3.1.By Step 2,we derive

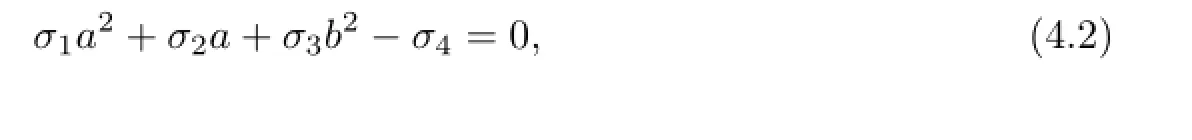
where σ1=0.042305453014301,σ2=9.203923632603722×10−6,σ3=0.042305453014301, σ4=0.002827314617277.Let b=0.Then a=±0.258408116608976.In this example,we choose a=0.258408116608976.Following Steps 3–5,we obtain

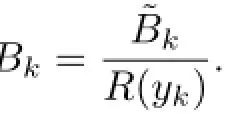
Table 4.1 Nodes and weights of Q4,7[f]with prescribed nodes in(4.1)

Remark 4.1In this example,there are in fi nite quadrature formulae with real and distinct additional nodes yk,as long as the real numbers a and b satisfy(4.2).

Example 4.2m=3,n=4.The maximum degree dmax(3,4)=5.The nodes xjare chosen as zeros of Chebyshev polynomials of the second kind of degree 3:

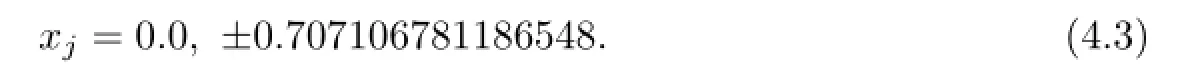
Simple calculation shows that the corresponding function R3(θ)is odd.Thus,set

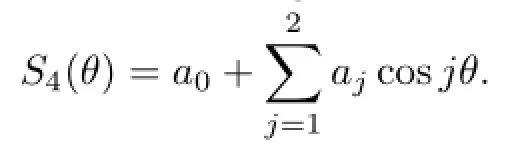
The solution of system(2.4){is

Set a1=1.Then we obtain the desired quadrature formula which is denoted by Q3,4[f]. The detail result is shown in Table 4.2.

Table 4.2 Nodes and weights of Q3,4[f]with prescribed nodes in(4.3)

Example 4.3m=3,n=5.The maximum degree dmax(3,5)=6.The nodes xjare also chosen as

Similarly,set

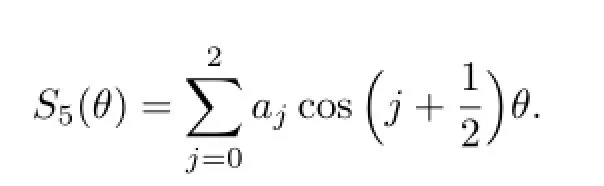
The solution of system(2.4)is

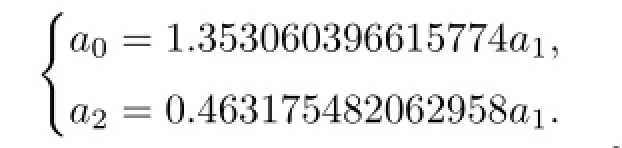
Set a1=1.The desired quadrature formula,denoted by Q3,5[f],is shown in Table 4.3.

Table 4.3 Nodes and weights ofwith prescribed nodes in(4.4)

Table 4.3 Nodes and weights ofwith prescribed nodes in(4.4)

xjweights yjweights 0.0 0.688022010196300 ±1.481760638771029 0.803968322230657 ±0.707106781186548 0.739532141369877 ±2.302882252246239 0.833463011424599 3.141592653589793 0.841236346933021

Example 4.4m=5,n=8.The maximum degree dmax(5,8)=10.The nodesare chosen randomly as

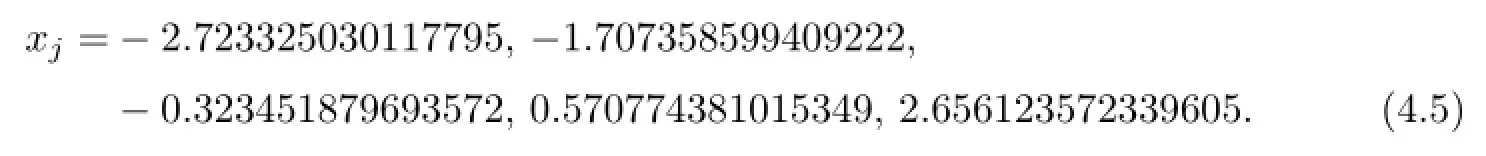
Set

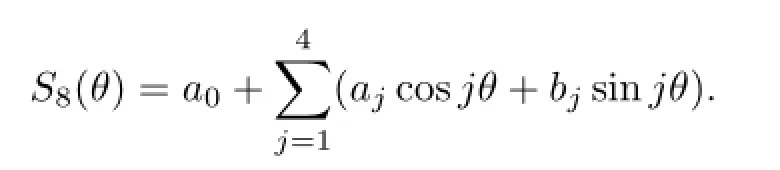
Set b4=1.The desired quadrature formula,denoted by Q5,8[f],is shown in Table 4.4.

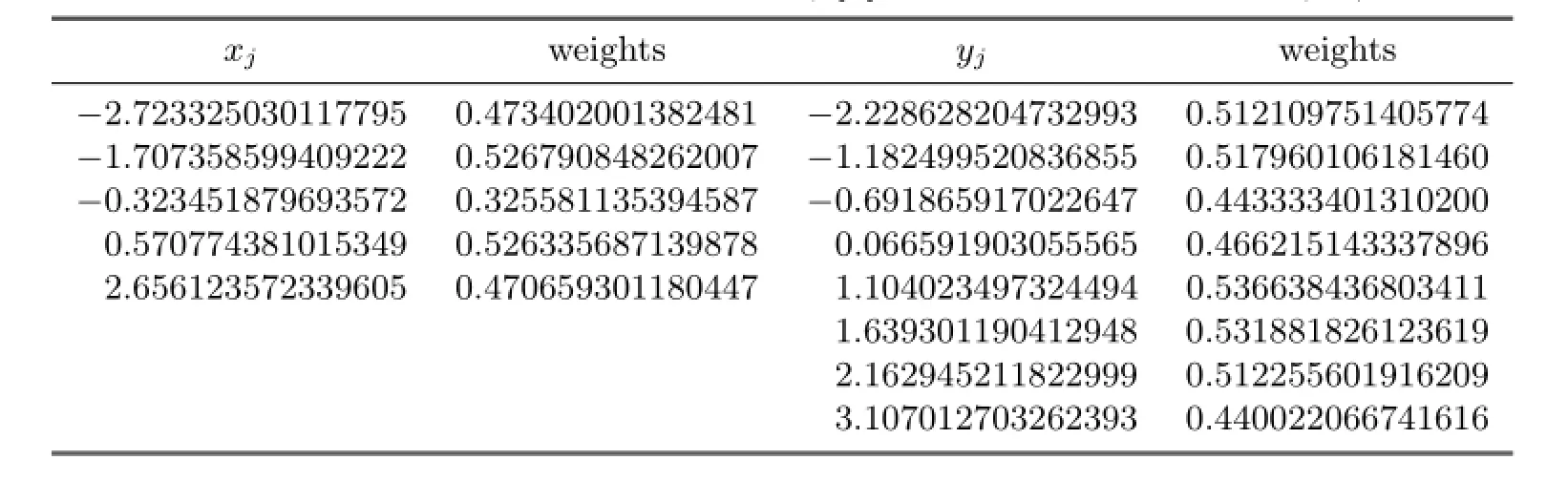
Table 4.4 Nodes and weights of Q5,8[f]with prescribed nodes in(4.5)

5 Conclusion

In this paper,the maximum trigonometric degree of quadrature formula with m prescribed nodes and n unknown additional nodes is studied and given in Theorem 2.1.Especially,when m is odd,(2.3)shows that for m and m+1,the maximum degrees are the same for any positive integer n.Furthermore,for even m,we give necessary and sufficient conditions for the existence of simple additional nodes and a constructive method to compute these nodes and all the weights.Numerical examples show that all the constructed formulae are desired quadrature formulae for both even and odd m.We further study the positivity of weights theoretically.

[1]Jagels C,Reichel L.Szeg¨o-Lobatto quadrature rules.J.Comput.Appl.Math.,2007,200: 116–126.

[2]Bultheel A,Daruis L,Gonz´alez-Vera P.Quadrature formulas on the unit circle with prescribed nodes and maximal domain of validity.J.Comput.Appl.Math.,2009,231:948–963.

[3]Curto R E,Fialkow L A.Recursiveness,positivity,and truncated moment problems.Houston J.Math.,1991,17:317–325.

[4]Curto R E,Fialkow L A.Solution of the Truncated Complex Moment Problem for Flat Data. Providence,RI,USA:American Mathematical Society,1996.

[5]Curto R E,Fialkow L A.Flat extensions of positive moment matrices:Relations in analytic or conjugate terms.Oper.Theory Adv.Appl.,1998,104:59–82.

[6]Curto R E,Fialkow L A.Flat Extensions of Positive Moment Matrices:Recursively Generated Relations.Providence,RI,USA:American Mathematical Society,1998.

[7]Curto R E,Fialkow L A.The quadratic moment problem for the unit circle and unit disk. Integral Equations Operator Theory,2000,38:377–409.

[8]Curto R E,Fialkow L A.The truncated complex K-moment problem.Trans.Amer.Math. Soc.,2000,352:2825–2855.

[9]Curto R E,Fialkow L A.Solution of the singular quartic moment problem,J.Operator Theory, 2002,48:315–354.

[10]Cruz-Barroso R,Daruis L,Gonz´alez-Vera P,Nj˚astad O.Quadrature rules for periodic integrands.Bi-orthogonality and para-orthogonality.Ann.Math.Inform.,2005,32:5–44.

[11]Cruz-Barroso R,Gonz´alez-Vera P,Nj˚astad O.On bi-orthogonal systems of trigonometric functions and quadrature formulas for periodic integrands.Numer.Algorithms,2007,44:309–333.

[12]Jones W B,Nj˚astad O,Thron W J.Moment theory,orthogonal polynomials,quadrature, and continued fractions associated with the unit circle.Bull.London Math.Soc.,1989,21: 113–152.

tion:42A15,65D30,65D32,47A57

A

1674-5647(2014)04-0334-11

10.13447/j.1674-5647.2014.04.07

Received date:May 2,2012.

Foundation item:The NSF(61033012,10801023,10911140268 and 10771028)of China.

E-mail address:zxluo@dlut.edu.cn(Luo Z X).