A Weak Convergence Theorem for A Finite Family of Asymptotically Nonexpansive Mappings

(School of Mathematics and Physics,Suzhou University of Science and Technology, Suzhou,Jiangsu,215009)

A Weak Convergence Theorem for A Finite Family of Asymptotically Nonexpansive Mappings

KAN XU-ZHOU AND GUO WEI-PING

(School of Mathematics and Physics,Suzhou University of Science and Technology, Suzhou,Jiangsu,215009)

Communicated by Ji You-qing

The purpose of this paper is to prove a new weak convergence theorem for a fi nite family of asymptotically nonexpansive mappings in uniformly convex Banach space.

asymptotically nonexpansive mapping,weak convergence,common f i xed point,uniformly convex Banach space

1 Introduction and Preliminaries

Throughout this paper,we assume that E is a real Banach space,E∗is the dual space of E and J:E→2E∗is the normalized duality mapping de fi ned by

where〈·,·〉denotes duality pairing between E and E∗.A single-valued normalized duality mapping is denoted by j.

Let K be a nonempty subset of E and T:K → K be a mapping.T is said to be asymptotically nonexpansive(see[1])if there exists a sequence{hn}⊂[1,∞)withhn= 1 such that

Proposition 1.1[2]LetKbe a nonempty subset ofE,andK→KbeNasymp-totically nonexpansive mappings.Then there exists a sequence{hn}⊂[1,∞)withhn→1

such that

Let K be a nonempty closed convex subset of E,x0∈K be any given point and:K→K be N asymptotically nonexpansive mappings.Let{hn}be the sequence de fi ned by(1.1)and L=Then the sequence{xn}⊂K de fi ned by

is called the implicit iterative sequence for a fi nite family of asymptotically nonexpansive mappingswherefor all n≥1 and some τ＞0.

Note that each n≥1 can be written as n=(k−1)N+i,where i=i(n)∈{1,2,···,N}, and k=k(n)≥1 is a positive integer with k(n)→∞as n→∞.Hence we can write(1.2) in the following compact form:

In 2006,Changet al.[2]studied the iteration process(1.3)and proved the following weak convergence theorem.

(ii)There exist constantsτ1,τ2∈(0,1)such that

Then the implicit iterative sequence{xn}de fi ned by(1.3)converges weakly to a common fi xed point of{T1,T2,···,TN}inK.

Only Theorem 1.1 has been obtained from the weak convergence problem for the sequence de fi ned by(1.3).The purpose of this paper is to prove a new weak convergence theorem of the iteration scheme(1.3)for N asymptotically nonexpansive mappings in a uniformly convex Banach space.

In order to prove our main results,the following concepts and lemmas are needed. A Banach space E is said to have a Fr´echet di ff erentiable norm(see[3]),if for all

the limit

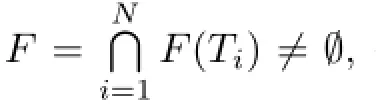
(ii)There exist constantsτ1,τ2∈(0,1)such that

Then

(1)the limitexists for allp∈F;

Lemma 1.2[5]LetEbe a real uniformly convex Banach space,Kbe a nonempty closed convex subset ofE,andT:K → Kbe an asymptotically nonexpansive mapping.ThenI−Tis demiclosed at zero,i.e.,for each sequence{xn}inK,if{xn}converges weakly toq∈Kand{(I−T)xn}converges strongly to0,then(I−T)q=0.

Lemma 1.3[6]LetXbe a uniformly convex Banach space andCbe a convex subset ofX. Then there exists a strictly increasing continuous convex functionγ:[0,∞)→[0,∞)withγ(0)=0such that for eachS:C→Cwith Lipschitz constantL,one has

2 A Weak Convergence Theorem

In this section,we prove a new weak convergence theorem of the iterative scheme(1.3)for N asymptotically nonexpansive mappings in uniformly convex Banach spaces.

exists.

Proof.Set an(t)=‖txn+(1−t)q1−q2‖.Thenfor alln≥1and someτ＞0.Then for allq1,q2∈F,the limit

exist by Lemma 1.1.It,therefore,remains to prove the Lemma 2.1 for all t∈(0,1).

For all n≥1 and any given x∈K,we de fi ne the mapping Ax,n−1:K→K by

Then

De fi ne the mapping Hn:K→K by

where I is the identity mapping.Using(2.3)and(1.3),we obtain

and

It follows from(2.4)–(2.5)and τ≤(1−αn+1)hk(n+1)≤(1−τ)L＜1 that

Lettingµn=hk(n)−1 and by(2.3),we have

and so

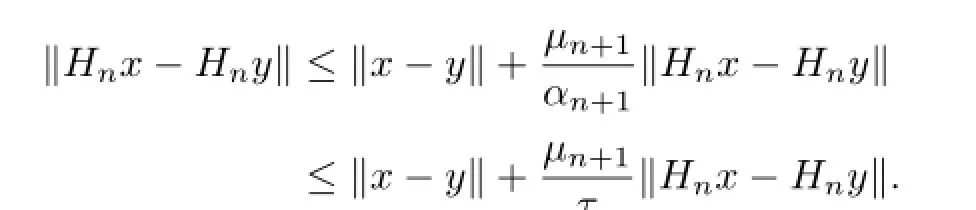
This implies that

By(2.7)and(2.8),we obtain

Let

By using(2.9)and Lemma 1.3,we have

So,

That is,

exists for all t∈(0,1).This completes the proof.

Proof.This follows basically as in the proof of Lemma 3.2 in[7]using Lemma 2.1 instead of Lemma 3.1 in[7].

Theorem 2.1Under the assumptions of Lemma2.2,then{xn}converges weakly to a common fi xed point of{T1,T2,···,TN}.

Proof.Since E is re fl exive and{xn}is bounded by Lemma 1.1,there exists a subsequence {xnk}of{xn}which converges weakly to some q∈K.By Lemma 1.1,we have

It follows from Lemma 1.2 that q∈F.

Now,we prove that{xn}converges weakly to q.Suppose that there exists some subsequence{xmj}of{xn}such that{xmj}converges weakly to some q1∈K.Then by the same method as given above,we can also prove that q1∈F.So q,q1∈F∩Ww(xn).It follows from Lemma 2.2 that

Therefore,q1=q.This shows that{xn}converges weakly to q.This completes the proof.

[1]Goebel K,Kirk W A.A fi xed point theorem for asymptotically nonexpansive mapping.Proc. Amer.Math.Soc.,1972,35:171–174.

[2]Chang S S,Tan K K,Lee H W J,Chan C K.On the convergence of implicit iteration process with error for a fi nite family of asymptotically nonexpansive mappings.J.Math.Anal.Appl., 2006,313:273–283.

[3]Osilike M O,Udomene A.Demiclosedness principle and convergence theorems for strictly pseudocontractive mappings of Browder-Petryshyn type.J.Math.Anal.Appl.,2001,256:431–445.

[4]Guo W P,Cho Y J.On the strong convergence of implicit iteration processes with errors for a fi nite family of asymptotically nonexpansive mappings.Appl.Math.Lett.,2008,21:1046–1052.

[5]Chang S S,Cho Y J,Zhou H Y.Demi-closed principle and weak convergence problems for asymptotically nonexpansive mappings.J.Korean Math.Soc.,2001,38:1245–1260.

[6]Falset J G,Kaczor W,Kuczumow T,Reich S.Weak convergence theorems for asymptotically nonexpansive mappings and semigroups.Nonlinear Anal.,2001,43:377–401.

[7]Guo W P,Guo W.Weak convergence theorems for asymptotically nonexpansive nonselfmappings.Appl.Math.Lett.,2011,24:2181–2185.

tion:47H09,47H10

A

1674-5647(2014)04-0295-06

10.13447/j.1674-5647.2014.04.02

Received date:March 31,2012.

Foundation item:The NSF(11271282)of China.

E-mail address:kanxuzhou925@126.com(Kan X Z).