On the Structure of the Units of Group Algebra of Dihedral Group

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

On the Structure of the Units of Group Algebra of Dihedral Group

NAN JI-ZHU AND ZHANG SHUANG

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

Communicated by Du Xian-kun

In this paper,we completely determine the structure of the unit group of the group algebra of some dihedral groups D2nover the fi nite fi eld Fpk,where p is a prime.

group algebra,unit group,dihedral group

1 Introduction

Let F be a fi nite Galois fi eld of prime characteristic p,G a fi nite group and FG the group algebra of the fi nite group G over the fi eld F.Denote by U(FG)the unit group of FG.The main problems of the group algebra are decomposition of the group algebra.This suggests the related question: fi nd all idempotent elements,nilpotent elements and invertible elements of FG.All these elements play an important role in the representation theory of the fi nite groups.Clearly,there exist techniques to fi nd the decomposition of FG and the structure of FG when the characteristic of the fi eld F does not divide the order of the group G.However, very little is known about U(FG)discussed in[1]when the characteristic of the fi eld F is p and the order of the group is apm,where p is a prime,(a,p)=1 and a,m∈N0.It is well known that if G is a fi nite p-group and F is a fi eld of characteristic p,then V(FG)is a fi nite p-group of order|F||G|−1,where V(FG)is the subgroup of the unit group of FG consisting of the elements with augmentation 1.Let Fpkbe the Galois fi eld of pkelements.A basis for V(FpG)is determined,where Fpis the Galois fi eld of p-elements and G is an Abelian pgroup(see[2]).A basis for V∗(FG)is established when F is any fi eld of characteristic p and G is an Abelian p-group(see[3]),where V∗(FG)are the unitary units of V(FG).Also in[3],there are conditions provided when V∗(FG)is normal in V(FG).Let D2nbe the dihedral group of order 2n.The order of U(FpkD2pm)is determined and the structure of U(F3kD6), U(F5kD10)and U(F5kD20)have been established in terms of split extensions of elementary Abelian groups.But the relationship among U(FpkCn),U(FpkC2)and U(FpkD2n)is unclear. In this paper,we give some messages on the relationship among U(FpkCp),U(FpkC2)and U(FpkD2p)and the relationship among U(F2kC2n),U(F2kC2)and U(F2kD2n+1).Also,the structure of U(F2kD2n+1)and U(FpkD2p)are determined.

2 Preliminaries

In this section,we mainly introduce some elementary knowledge and notations used in this paper.

De fi nition 2.1[4]A circulant matrix over a fi eldFis a squaren×nmatrix which has the form

It is easy to see that all the n×n circulant matrices over a fi eld F form a commutative ring and the inverses of the circulant matrices are also circulant.

If G={g1,g2,···,gn}is a fi xed listing of the elements of a group G,then the matrix

is referred to as the matrix of G(relative to this listing)and denoted by M(G).Let

where F is a fi eld and αgi∈F.Then the matrix

is called the FG-matrix of ω and is denoted by M(FG,ω).In the following,we show that the map σ:ωM(FG,ω)is a ring homomorphism between FG and the n×n FG-matrices over F.

Lemma 2.1[4]Given a listing of the elements of a groupGof ordern,then there is a bijective ring homomorphism betweenFGand then×n FG-matrices overF.This bijective ring homomorphism is given byσ:ω→M(FG,ω).

Lemma 2.2[4]LetFbe a fi eld.Thenω∈FGis a unit if and only ifσ(ω)is a unit inMn(F).

Corollary 2.1[4]ω∈FGis a unit if and only ifσ(ω)is a unit inMn(F)that meansdet(σ(ω))is a unit inF.

Lemma 2.3[4]LetA=circ(α1,α2,···,αpm),whereαi∈Fpk,i=1,2,···,pm,andpa prime,m∈N0,whereN0is the positive natural number set.Then

Lemma 2.4[5]LetC2be a cyclic group of order2andFpka fi eld of characteristicp.Denote the unit group of the group algebraFpkC2byU(FpkC2).Then we have

3 Constructing the Unit Group of the Group Algebra of Dihedral Group

In this section,we establish the relationship among U(FpkD2n),U(FpkCn)and U(FpkC2), where F is a fi eld of characteristic p and p|n.

First we give the circulant matrix of D2n.Let D2n={1,a,a2,···,an−1,b,ab,···,an−1b}. By the results in Section 2,for any element

we have

Then

where A=circ(α0,α1,···,αn−1)and B=circ(β0,β1,···,βn−1),αi,βj∈Fpk,0≤i,j≤n−1.It is well known that D2nCnC2,where C2=〈x|x2=1〉.Thus we de fi ne the group homomorphism π:U(FpkD2n)→U(FpkC2)by

where αi,βj∈Fpk,i,j=0,1,···,n−1.Then it is easy to see that π is an epimorphism. De fi ne the group homomorphism θ:U(FpkC2)→U(FpkD2n)by

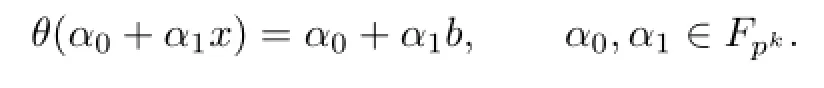
Then

Hence U(FpkD2n)is a split extension of U(FpkC2)by kerπ.Therefore,we have the theorem as follows.

Theorem 3.1LetFpkbe a fi eld of characteristicpandU(FpkD2n)the unit group of the group algebraFpkD2n.Then

(1)the order ofU(FpkD2n)isp2(n−1)k×(pk−1)2;

(2)V(FpkCn)is a subgroup of the kernel ofπ,and its order isp(n−1)k,whereV(FpkCn)is the subgroup of the unit group of the group algebraFpkCnof the cyclic groupCnwith augmentation1.

Proof.De fi ne π:U(FpkD2n)→U(FpkC2)by

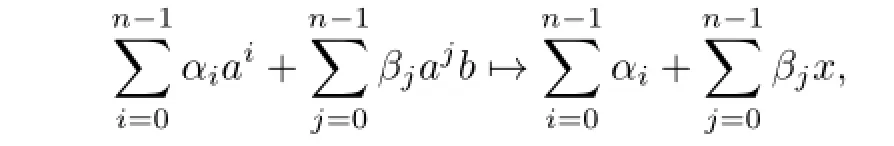
where C2={1,x|x2=1},αi,βj∈Fpk,i,j=0,1,2,···,n−1.Then π is a group epimorphism.Let θ:U(FpkC2)→U(FpkD2n)be a group homomorphism de fi ned by

Then

Hence U(FpkD2n)is a split extension of U(FpkC2)by kerπ.That is to say,U(FpkD2n)U(FpkC2)kerπ.Therefore,the order of U(FpkD2n)is|U(FpkC2)|×|kerπ|.For any element

we have ω∈kerπ if and only if

Theorem 3.2LetD2nbe the dihedral group andD2nCnC2,whereCnis the cyclic group of ordernandC2is the cyclic group of order2.Denote the unit group of group algebraFpkD2n,FpkCnandFpkC2byU(FpkD2n),U(FpkCn)andU(FpkC2),respectively.LetV(FpkCn)be the subgroup of the unit group of the group algebraFpkCnwith augmentation1.ThenV(FpkCn)U(FpkC2)is a subgroup ofU(FpkD2n)with indexp(n−1)k.

Proof.In fact,it is an immediate result of Theorem 3.1.

Theorem 3.3Letπ:U(FpkD2n)→U(FpkC2)be a group epimorphism de fi ned by

LetTbe a subgroup ofkerπconsisting of the elements with the form

ThenTis normal inkerπandU(FpkCn).Furthermore,Thas the indexinU(FpkD2n)and the indexinU(FpkCn).

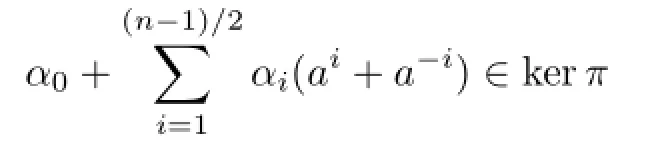
4 The Structure of U(F2kD2n+1)

Let D2n+1be the dihedral group of order 2n+1denoted by

In this section,we consider the structure of U(F2kD2n+1).When n=1,2,the structure of U(F2kD2n+1)has been determined.Therefore,we only consider the case of n≥3.Let m= 2n.It is well known that U(F2kD2m)V(F2kD2m)×F∗,and V(F2kD2m)=1+J(F2kD2m). Let θ:U(F2kD2m)→U(F2kCm),and de fi ned by

where Cmdenotes the cyclic group generated by c,and αi,βj∈F2k,i,j=0,1,···,m−1. It is easy to verify that θ is an epimorphism of group.

Let ϑ:U(F2kCm)→U(F2kD2m)be a group homomorphism de fi ned by

Obviously,

and

Denote the kernel of θ by H.Let

where αi,βj∈F2k,i,j=0,1,···,m−1.Then ω∈H if and only if

That is to say,

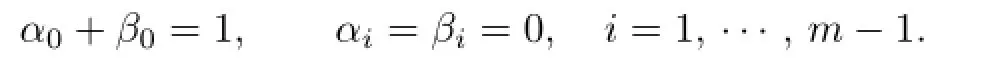
Hence the order of H is 2km.

Theorem 4.1Letπ:U(F2kD2m)→U(F2kC2)be the group homomorphism de fi ned by

whereαi,βj∈F2k,i,j=0,1,···,m−1.LetHbe a subset ofU(F2kD2m)with the elements in the form

ThenkerπH.

Proof.Since

and

where αi,βj∈F2k,i,j=0,1,···,m−1,we have

Hence,H is closed under the multiplication.It is easy to see that H is contained in the kernel of π and its order is 2km.So kerπ～=H.

Theorem 4.2Letπ:U(F2kD2m)→U(F2kC2)be the group homomorphism de fi ned by

whereαi,βj∈F2k,i,j=0,1,···,m−1.LetT1be the set with the elements in the form

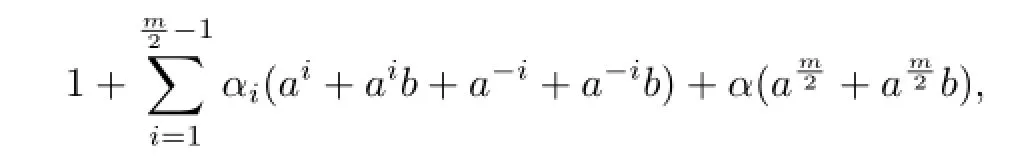
whereαi,α∈F2k,i=1,2,···,ThenT1is an Abelian group,

Proof.For any element

i.e.,

That is to say,T1is Abelian.On the other hand,for any element β(aj+ajb)with β∈F2k,

we have

HenceT1belongs to thecenter ofkerπ.Therefore we have T1◁kerπ.Itis easy to compute that the order ofisandhas exponent 2.Therefore

Theorem 4.3Letπ:U(F2kD2m)→U(F2kC2)be the group homomorphism de fi ned by

whereαi,βj∈F2k,i,j=0,1,···,m−1.LetT1be the set of the elements in the form of

whereα,∈i=1,2,···,−1.LetTbe the subset ofkerπconsisting of the2elements in the following form:

whereωis a fi xed element inF2kdi ff erent from1.ThenT1∩T2={1}andT1T2～=kerπ.

Proof.For any element

and

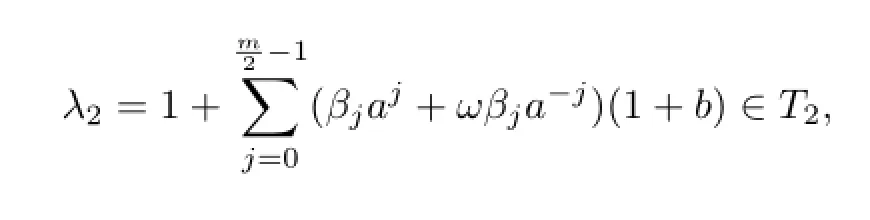
Hence T2is a subgroup of kerπ.Obviously,T1∩T2={1}and T1T2=T2T1=kerπ.By Theorem 4.2,it is easy to see that T1T2kerπ.

Theorem 4.4LetD2n+1be the dihedral group of order2n+1.Denote byU(F2kD2n+1)the unit group of the group algebra ofF2kD2n+1.LetT1be the set consisting of the elements of the form

whereα,αi∈F2k,i=1,2,···,−1,andT2be the subgroup of the form

where∈,j=0,1,···,−1,ω≠1.Thenm

Proof.By Theorems 4.1–4.3,the result is clear.

Up to now,we have shown that V(F2kC2)and U(F2kC2n)are the components of the semi-direct product of U(F2kD2n+1).

5 The Structure of the Unit Group of Group Algebra FpkD2p

De fi ne the group epimorphism θ:U(FpkD2p)→U(FpkC2)by

where C2=〈c|c2=1〉,αi,βj∈Fpk,i,j=0,1,···,p−1.

Let ϑ:U(FpkC2)→U(FpkD2p)be the group homomorphism de fi ned by

It is easy to see that

and U(FpkD2p)is a split extension of U(FpkC2)by kerθ.Thus

Let

in U(FpkD2p),where αi,βj∈Fpk,i,j=0,1,···,p−1.Then ω∈kerθ if and only if

Thus

Lemma 5.1Letθ:U(FpkD2p)→U(FpkC2)be a group homomorphism de fi ned by

whereC2=〈c|c2=1〉,αi,βj∈Fpk,i,j=0,1,···,p−1.Denote byHthe kernel ofθ.ThenHhas exponentp.

Proof.Let

where αi,βj∈Fpk,i,j=0,1,···,p−1.Then we have

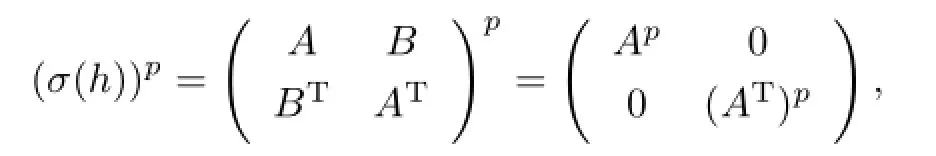
where A=circ(α0,α1,···,αp−1),B=circ(β0,β1,···,βp−1).By Lemma 2.3,we have

Lemma 5.2Letθ:U(FpkD2p)→U(FpkC2)be a group homomorphism de fi ned by

whereC2=〈c|c2=1〉,αi,βj∈Fpk,i,j=0,1,···,p−1,andHbe the kernel ofθ.

Then

Proof.Let

where αi,βj∈Fpk,i,j=0,1,···,p−1.Then

if and only if

Thus any element of CH(a)has the form

Let

Then

where

Therefore,CH(a)◁H.

Lemma 5.3Letθ:U(FpkD2p)→U(FpkC2)be a group homomorphism de fi ned by

whereC2=〈c|c2=1〉,αi,βj∈Fpk,i,j=0,1,···,p−1,andTbe the set consisting of the elements of the form

whereαi∈Fpk,i=0,1,···,p−1.Then

Proof.Let

Therefore,T is closed under the multiplication.

On the other hand,

Thus t1t2=t2t1,and T is Abelian.

Next,

if and only if

That is to say,the order of T is p(p−2)k.Thus T

Lemma 5.4Letθ:U(FpkD2p)→U(FpkC2)be a group homomorphism de fi ned by

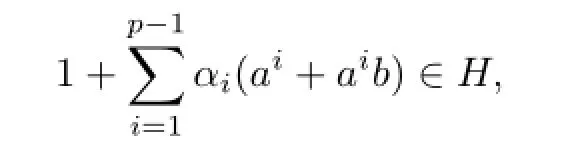
whereαi∈Fpkand=0.ThenHCH(a)T.

Proof.By the de fi nition,it is easy to see that CH(a)∩T={1}.By the Isomorphism Theorem,

Thus we have

and

On the other hand,|H|=p2(p−1)k.Therefore,

Theorem 5.1LetD2pbe the dihedral group of order2p.Denote the unit group of the group algebraFpkD2pbyU(FpkD2p).Then

Proof.Through the extension constructed prior,we have

By Lemma 5.4,

and by Lemma 2.3,it is easy to know

So,

[1]Bovdi V A,Kovacs L G.Unitary units in modular group algebras.Manuscripta Math.,1994,84(1):57–72.

[2]Sandling R.Units in the modular group algebra of a fi nite Abelian p-group.J.Pure Appl. Algebra,1984,33:337–346.

[3]Bovdi A,Szakacs K.A Basis for the Unitary Subgroup of the Group Algebra of Units in a Finite Commutative Group Algebra.Debrecen:Publ.Math.,1995,46(1/2):97–120.

[4]Hurley T.Group rings and rings of matrices.Int.J.Pure Appl.Math.,2006,31:319–335.

[5]Gildea J.The structure of U(F5kD20).Int.J.Pure Appl.Math.,2010,8:153–160.

tion:22D20,20F05

A

1674-5647(2014)04-0307-13

10.13447/j.1674-5647.2014.04.04

Received date:Nov.2,2011.

Foundation item:The NSF(10671028)of China.

E-mail address:jznan@163.com(Nan J Z).