The Almost Split Sequences for Trivial Extensions of Hereditary Algebras

(1.College of Applied Sciences,Beijing University of Technology,Beijing,100124)

(2.Department of Mathematics,Chengdu Normal University,Chengdu,611130)

The Almost Split Sequences for Trivial Extensions of Hereditary Algebras

ZHANG YU-LIN1,2AND YAO HAI-LOU1,*

(1.College of Applied Sciences,Beijing University of Technology,Beijing,100124)

(2.Department of Mathematics,Chengdu Normal University,Chengdu,611130)

Communicated by Du Xian-kun

Let A be a basic hereditary artin algebra and R=AQ be the trivial extension of A by its minimal injective cogenerator Q.We construct some right(left) almost split morphisms and irreducible morphisms in modR through the corresponding morphisms in modA.Furthermore,we can determine its almost split sequences in modR.

hereditary algebra,trivial extension,AR sequence,irreducible morphism

1 Introduction

Let A be a basic hereditary artin algebra over its center C,I the injective envelope of C/RadC and Q the A-module HomC(A,I).Then the trivial extension R of A by Q is R=AQ.It is an additive group with the multiplication de fi ned by

From[1],we know the following conclusion about the module category of R=

Theorem 1.1[1]LetAbe a ring andManA-module.Then the categoriesmodAM, modAandHomAmodAare isomorphic.

By the above theorem we know that the modules of R=AQ are in the forms of(XQX)or(XHomA(Q,X))for X ∈modA.For the convenience,we just write HomAasSince A is a hereditary algebra,X=XQ⊕X/XQ.Let U=X/XQ and V =XQ.Then the above forms have the canonical expressions X=(U⊗AQV)and X=(U[Q,V]).Since A is hereditary,V is an injective A-module from its construction(see[2]).In this paper we mainly consider the modules in the fi rst form,i.e.,X=(U⊗AQV).In order to study the irreducible morphisms,it is essential to determine the indecomposable modules of R=AQ which has been researched in[2].

Proposition 1.1[2]LetAbe a hereditary artin algebra,Q=HomC(A,I)andR=AQ. Let(U⊗AQV)∈modbe a canonical expression of anR-moduleXwithψ≠0.ThenXis an indecomposableR-module if and only if either of the following conditions(1)and(2)is satis fi ed:

(1)ψis an isomorphism andUAis indecomposable and projective;

(2)ψis an epimorphism(but not monomorphism),UAis projective,kerψis a large submodule ofU⊗AQand is indecomposable.

In case(1)Xis a projective and injectiveR-module.

An indecomposable R-module X=(U⊗AQV)((U[Q,V]))is call it to be of 2nd kind(1st kind)if ψ≠0(ψ=0),and is same as ψ≠0(ϕ=0).There are also some consequences about R which can be seen in[3–4].

By the above theorem,proposition and the consequences about right(left)almost split morphisms and irreducible morphisms in[5–6],we construct the corresponding morphisms in modR.

To begin with the discussion we recall the description of morphisms between R-modules. Let X=and X′=(U(′⊗AQ)be R-modules.Any R-morphism from X to X′has the matrix expressionwhere α:U→U′,β:V→V′,γ:V→U′and δ:U→ V′are A-morphisms.At the same time,α and β are compatible with the following diagram:

From the construction of U′and V,we get that γ=0.

All algebras in this paper are hereditary algebras and the tensor products are in the algebra A.

2 The Almost Split Morphisms over R=AQ

In this section,we construct some right(left)almost split morphisms over R=AQ from the ones in modA.

Proposition 2.1ForR=AQ,we have

(1)LetX,YbeA-modules andYnonprojective.If the monomorphismf:X → Yis right almost split inmodA,then(0,f):(0→ X)→ (0→ Y)is a right almost split morphism inmodR;

(2)LetX,YbeA-modules andYnonprojective.Iff:X→Yis right almost split inmodA,then(f,0):(X⊗Q→0)→(Y⊗Q→0)is a right almost split morphism inmodR;

(3)LetX,YbeA-modules andXnoninjective.Iff:X→Yis left almost split inmodA,then(0,f):(0→X)→(0→Y)is a left almost split morphism inmodR;

(4)LetX,YbeA-modules andXnoninjective.If the monomorphismf:X→Yis left almost split inmodA,then(f,0):(X⊗Q→0)→(Y⊗Q→0)is a left almost split morphism inmodR.

Proof.(1)Since f is right almost split,we know that f is not a split epimorphism.Thus, (0,f)is also not a split epimorphism.We show that,for any indecomposable R-module (U⊗QV)and nonisomorphism(δ,h):(U⊗QV)→(0→Y),where δ:U→Y, h:V→Y and h is compatible with the following commutative diagram:

(δ,h)factors through(0,f).We prove it in two cases:

A-module and δ=0.Since(0,f)is nonisomorphic,f is also a nonisomorphism.So,there exists an A-morphism k:U→ X such that h=fk.It is easy to know that(0,h)is an R-morphism and(0,h)=(0,f)(0,k).Thus,(δ,h)factors through(0,f)in the fi rst case.

In conclusion,(0,f)is a right almost split morphism.

(2)The proof is similar to that of(1).

(3)Similarly,as the proof of(1),we show that for any indecomposable R-module(U⊗ QV)and nonisomorphism(0,h):(0→X)→(U⊗QV),where h:X→V and h is compatible with the following commutative diagram:(0,h)factors through(0,f).We prove it in two cases.

(a)If ϕ=0,then the proof is similar to that of(1).

(4)The proof is similar to(1)and(3).

is a right almost split morphism in modR,and

is a left almost split morphism inmodR,wherei:rU→Uis the embedding morphism, j:U→U/socUis the natural epimorphism.

Proof.From Proposition 1.1,(U⊗QU⊗Q)is an indecomposable projective and injective R-module.RadR=RadA⊕Q,so

Thus,

is right almost split.At the same time,for the indecomposable injective R-module(U⊗Qψ−→U⊗Q),

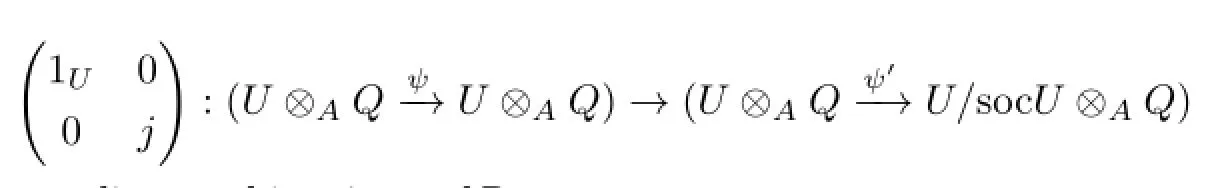
is a left almost split morphism in modR.

Proposition 2.2ForR=AQ,we have the following:

(1)LetXandYbeA-modules andYnonprojective.If the monomorphismf:X→Yis right almost split inmodA,then(0,f):(C⊗QX)→(Y⊗Q→0)is a right almost split morphism inmodR;

(2)LetXandYbeA-modules.Suppose that the epimorphismf:X → Yis a left almost split morphism inmodA.For the indecomposableR-module(Y⊗QX),if

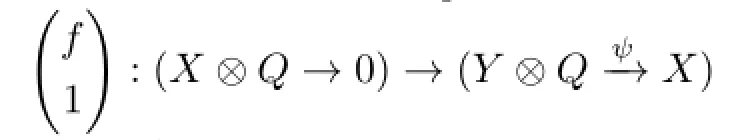
is anR-morphism,then it is a left almost split morphism inmodR;

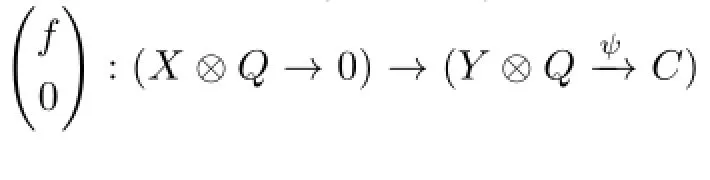
Proof.(1)Similarly,as the proof of Proposition 2.1,let(U⊗QV)be any indecomposable R-module and(δ,h):(U⊗QV)→(0→Y)be any nonisomorphism,where δ:U→Y,h:V→Y and h is compatible with the following commutative diagram:

We know that neither h nor δ is a split epimorphism.Then there exist A-morphisms k:V→X and δ′:U→X such that h=fk and δ=fδ′.Since f is a monomorphism and from(2.3),it is clear that kϕ=0,we have the following diagram:

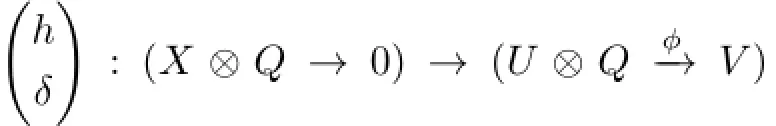
(a)If ϕ=0,it is obvious;

(b)If ψ≠0,then h is not a split monomorphism.if h is a split monomorphism from (2.5)we get that ϕ(h⊗1Q)=0.Hence,(X⊗Q→0)is a direct summand of(U⊗QV). It contradicts that(U⊗QV)is an indecomposable R-module.So,there exists an A-morphism k:Y→ U such that h=kf.Since f is an epimorphism,f⊗1Qis also an epimorphism.Then we have that ϕ(k⊗1Q)=0 because ϕ(h⊗1Q)=ϕ(k⊗1Q)(f⊗1Q)=0. This means that we have the following diagram:

(3)The proof is similar to that of(1).

Theorem 2.2ForR=AQ,we have the following:

(1)If the epimorphismf:V→V′is right almost split inmodAand for the indecomposableR-module(U⊗QV′)withV′nonprojecitve,there existsg:V′→Vsuch thatfg|Imψ=1Imψ,then

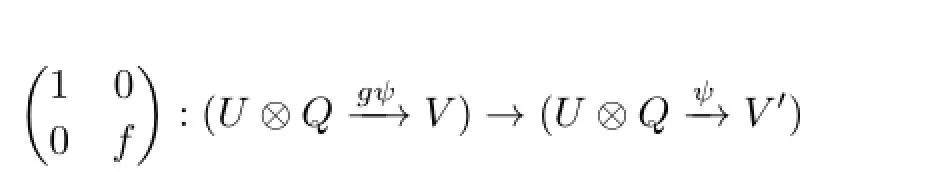
is right almost split inmodR;

(2)Ifg:V→V′is left almost split inmodA,then for the indecomposableR-module(U⊗QV)withψ≠0,

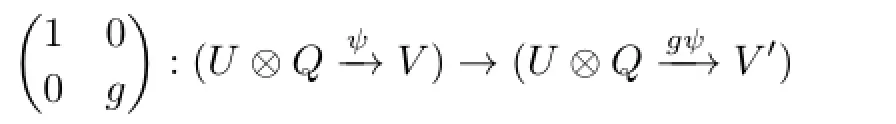
is left almost split inmodR.

Proof.(1)Similarly,as the proof of Proposition 2.1,let(X⊗QY)be any indecomposable R-module andbe any nonisomorphism, where α:X→U,δ:X→V′and β:Y→V′.At the same time,α and β are compatible with the following commutative diagram:

(1)If ϕ=0,it is obvious.

(2)If β is a split epimorphism,then there exists an A-module V1such that Y～=V′⊕V1. Since A is a hereditary algebra,Imα⊆U is projective.Thus,Imα is a direct summand of projective A-module X.So there exists an A-module C such that X⊗Q～=(Imα⊗Q)⊕(C⊗Q).From(2.7)we can see that ϕ(C⊗Q)=V1.Hence(Imα⊗QV′)is isomorphic to a direct summand of(X⊗QY).It is a contradiction.So,we know that β is not a split epimorphism.Since V′is nonprojecitve,δ is also not a split epimorphism.Then for the almost split morphism f,there exist A-morphisms β′:Y→V and δ′:X→V such that β=fβ′and δ=fδ′.From(2.7)we get that βϕ=ψ(α⊗1).Hence gβϕ=gψ(α⊗1)=β′ϕ because g|Imψis a monomorphism.It means thatis an R-morphism.Meanwhile

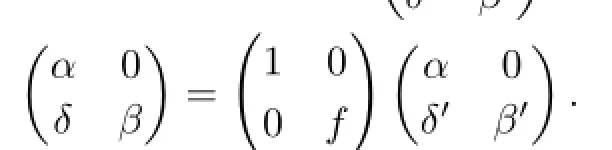
(2)Similarly,as the proof of(1),let(X⊗QY)be any indecomposable R-module and:(U⊗QV)→(X⊗QY)be any nonisomorphism.For

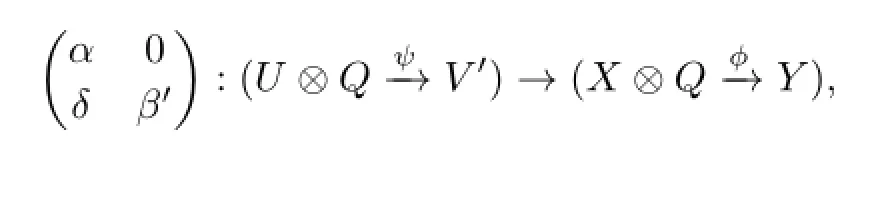
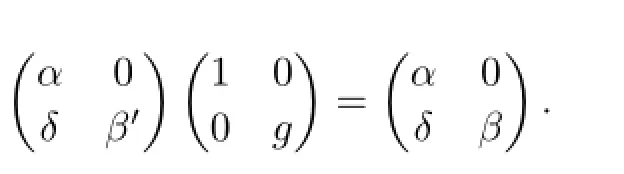
where β=β′g,we have that is left almost split in modR.

Up to now we can construct some almost split morphisms in modR from the corresponding morphisms in modA.In the next section the irreducible morphisms in modR will be constructed in the similar way.

3 The Irreducible Morphisms over R=AQ

From[2],we have the following lemma to judge the irreducible morphisms between the indecomposable R-modules of 2nd kind.

Lemma 3.1[2]LetX=(U⊗QV)andX′=(U′⊗QV′)be indecomposableR-modules of2nd kind andθ:X → X′anR-morphism.Letθ′:kerψ→ kerψ′be theA-morphism induced byθ.Thenθis irreducible if and only ifθ′is irreducible.

So,in this section we construct irreducible morphism between the indecomposable R-modules of 1st kind and 2nd kind.

Proposition 3.1LetXandYbe indecomposableA-modules.Then we have the following:

(1)If the epimorphismf:X→Yis irreducible inmodA,then

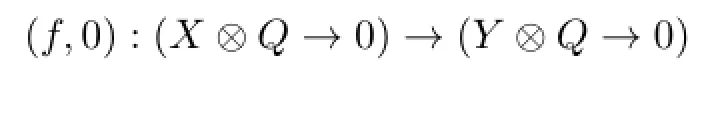
is irreducible inmodR;

(2)If the monomorphismf:X→Yis irreducible inmodA,then

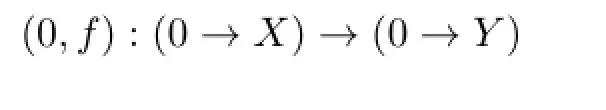
is irreducible inmodR.

Proof.(1)We prove it in two steps by the de fi nition of an irreducible morphism.

(I)As f is neither a split monomorphism nor a split epimorphism,it is easy to see that the same conclusion is true for(f,0);

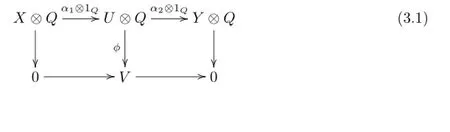
(a) If α1is a split monomorphism,then there existssuch that=1X.By (3.1)we know that Imα⊆kerϕ.So(X⊗Q→0)is isomorphic to a direct summand of (U⊗QV).Furthermore,we have that

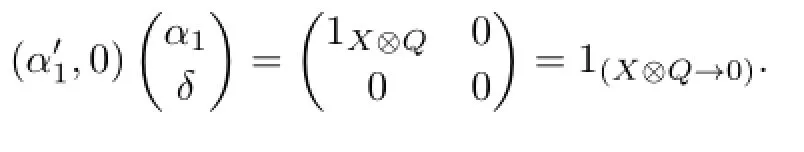
(b)If α2is a split epimorphism,then there exist an A-module C such that

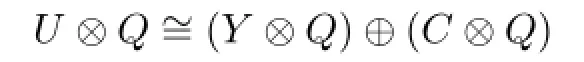
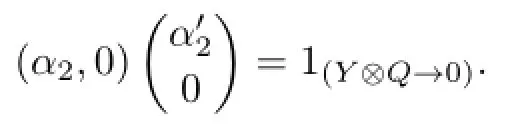
It means that(α2,0)is a split epimorphism.

In conclusion,(f,0)is irreducible in modR.

(2)Similarly,as the proof of(1),we have the following diagram:

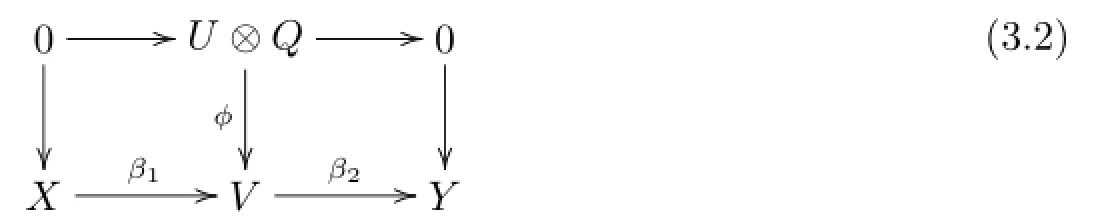
(a)If β1is a split monomorphism,then there exists an A-module X′such that V～= X⊕X′.From(3.2)we know that β2ϕ=0.So,X∩Imϕ={0}because f is a monomorphism. Hence(0→X)is isomorphic to a direct summand of(U⊗QV).It is easy to know that (0,β1)is a split monomorphism.

(b)If β2is a split epimorphism,it is not hard to see that(δ,β2)is a split epimorphism. In conclusion,(0,f)is irreducible in modR.

Theorem 3.1(1)LetXbe an indecomposableA-module andYan indecomposable projectiveA-module.If the monomorphismf:X→Yis an irreducible morphism inmodA,then

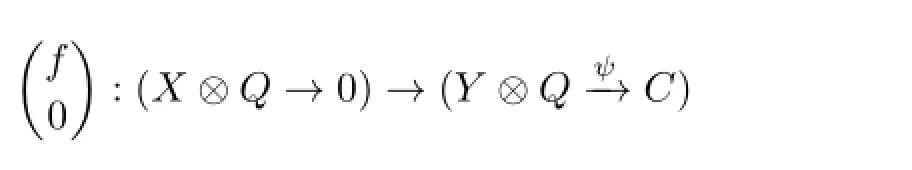
is irreducible inmodR;

(2)LetYbe an indecomposableA-module,andXan indecomposable projectiveA-module.If the epimorphismf:X→Yis an irreducible morphism inmodA,then

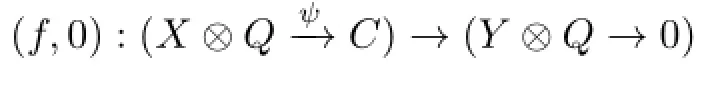
is irreducible inmodR.

Proof. (1)Similarly,as the proof of Proposition 3.1,let(U⊗?V)be an R-module,

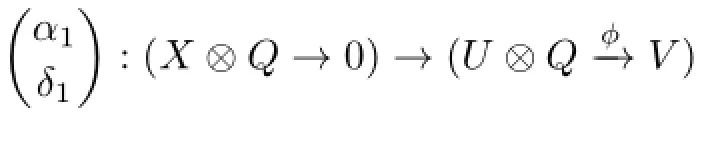
and

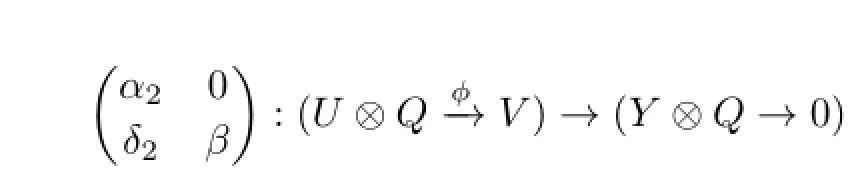
(a)If α1is a split monomorphism,then from(3.3)we know that ϕ(α1⊗1Q)=0.It means that X⊗QIm(α1⊗1Q)⊆kerϕ.Thus,(X⊗Q→0)is isomorphic to a direct summand of(U⊗QV).Furthermore,we have that

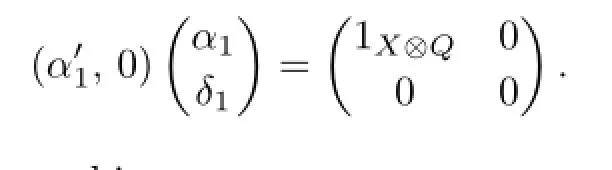
(b)If α2is a split epimorphism,then there exist an A-module D such that U⊗Q(Y⊗Q)⊕(D⊗Q)and an A-morphismsuch that α=1Y.At the same time,we have the following diagram:

Since f is a monomorphism,α1is also a monomorphism.From(3.3)we see that Imα1⊆kerϕ∩kerψ0.So,θ is a split epimorphism because kerψ is essential in an injective A-module Y⊗Q and A is hereditary.Hence,α2and β are split epimorphisms.Then there exists an A-morphism β′:C→V such that ββ′=1C.It is easy to see that α′and β′are compatible with

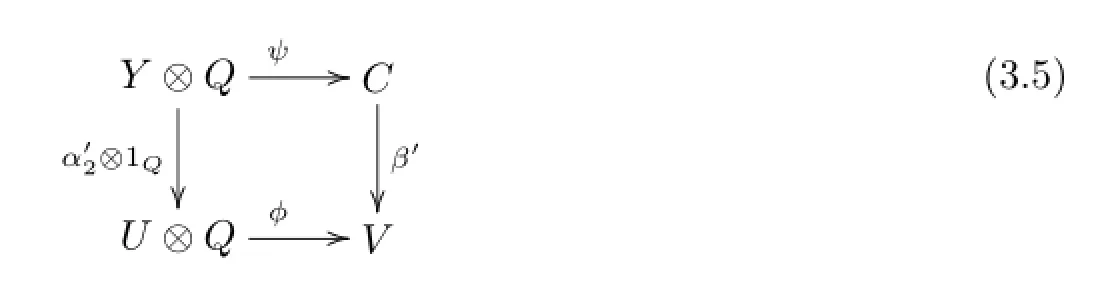
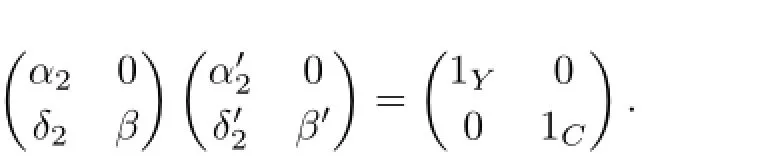
(2)This follows from duality.

Tachikawa[2]computed the forms of DTrRX and TrDRX of the indecomposable R-module X.So combining the right(left)almost split morphisms and irreducible morphisms with it,we can construct the AR-sequence.For example,we have the following corollary.

Corollary 3.1(1)IfYis a nonprojective indecomposableA-module andg:X→Y→0is irreducible inmodA,then

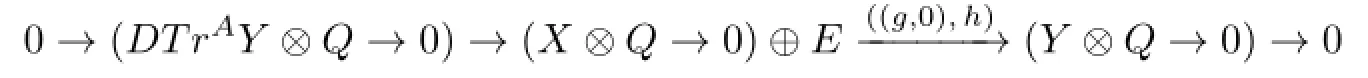
is an almost split sequence inmodR,whereEis anR-module.

(2)IfXis a noninjective indecomposableA-module andg:0→X→Yis irreducible inmodA,then

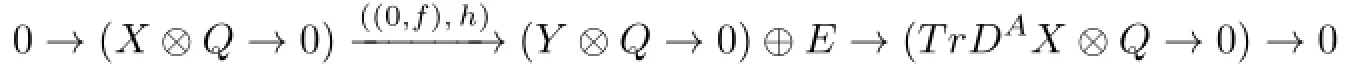
is an almost split sequence inmodR,whereEis anR-module. Proof.We only prove(1);the proof of(2)is similar.

From Proposition 3.1,(f,0)is irreducible in modR.So

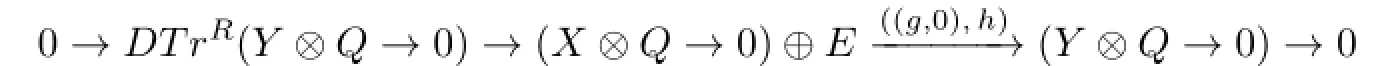
is an almost split sequence in modR,where E is an R-module.We have DTrAYDTrRY, by Proposition 2.2 in[2].Then,it is easy to get the corollary.

[1]Fossum R M,Griffith P A,Reiten I.Trivial Extensions of Abelian Categories.New York: Springer-Verlag,1975.

[2]Tachikawa H.Representations of trivial extensions of hereditary algebras.Lecture Notes in Math.,1980,832:579–599.

[3]Yamagata K.Extension over hereditaty artinain rings with self-dualities I.J.Algebra,1981,73(2):386–433.

[4]Yamagata K.Extension over hereditaty artinain rings with self-dualities II.J.London Math. Soc.(2),1982,26(2):25–36.

[5]Auslander M,Reiten I,Smalø S O.Representation Theory of Artin Algebras.New York:Cambridge Univ.Press,1995.

[6]Assem I,Simson D,Skowronski A.Elements of the Representation Theory of Associative Algebras.New York:Cambridge Univ.Press,2006.

[7]Zhang Y,Yao H.The almost split sequences and D-split sequences of T2(T).J.Math.Res. Appl.,2003,33(1):11–22.

tion:16G20,16G60

A

1674-5647(2014)04-0369-10

10.13447/j.1674-5647.2014.04.10

Received date:May 30,2012.

Foundation item:The NSF(11271119)of China and the NSF(1122002)of Beijing.

*Corresponding author.

E-mail address:zhanglinxxby@163.com(Zhang Y L),yaohl@bjut.edu.cn(Yao H L).