Painlev´e Property and Integrability of Polynomial Dynamical Systems

,*

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun,130012)

Painlev´e Property and Integrability of Polynomial Dynamical Systems

LI WEN-LEI1,2AND SHI SHAO-YUN1,2,*

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun,130012)

The main purpose of this paper is to investigate the connection between the Painlev´e property and the integrability of polynomial dynamical systems.We show that if a polynomial dynamical system has Painlev´e property,then it admits certain class of fi rst integrals.We also present some relationships between the Painlev´e property and the structure of the di ff erential Galois group of the corresponding variational equations along some complex integral curve.

Painlev´e property,integrability,di ff erential Galois group

1 Introduction

The connection between the integrability of dynamical systems and the singularity structure of their solutions was fi rst discovered since the pioneer work of Kowalevskaya[1]in studying the problem for the motion under gravity of a rigid body about a fi xed point.The remarkable insight of Kowalevskaya is that the concerned problem can be solved explicitly whenever the parameters are taken such that the dependent variables are meromorphic with respect to the time t in the complex plane.It is well known that the solvable cases are the four integrable cases of the Heavy top problem(see[2]):isotropic,Euler,Lagrange and Kowalevskaya. The idea of Kowalevskaya was trying to detect the regular property of dynamical systems by studying the singular structure of their solutions.So far,one of the famous singular analysis results is the Painlev´e analysis,which detects the Painlev´e property of a given system established by Painlev´e and some other mathematicians following his work.Generallyspeaking,a dynamical system is integrable if it has sufficient number of fi rst integrals such that its general solution can be solved by quadratures,while a given system has Painlev´e property if its general solution has no movable critical singular points on the complex plane. Since 80th decade of the last century,there have been numerous references and reports for the successful developments and applications of Painlev´e analysis,such as[3–10]and so on.Among of these results,an interesting phenomenon is that many concerned systems passing the Painlev´e test always turn to be integrable,which implies the deep relationships between integrability and Painlev´e property,and a natural question should be asked that, what is the exact connection between the integrability and the Painlev´e property for general dynamical systems?One of the famous results is due to Yoshida[11–12]who studied the connection between the integrability of dynamical systems and corresponding Kowalevskaya exponents with respect to a balance.Following Yoshida’s work,many results have been obtained on the connection between the integrability,partial integrability,non-integrability of dynamical systems and corresponding Kowalevskaya exponents,see[13–16]for example. However,nearly all these results are the necessary conditions for the integrability,partial integrability and non-integrability of dynamical systems,i.e.,the idea of these results are from integrability to the singularity property.

About several years after the Kowalevskaya’s work,Liapounov[2]proved that the only cases of the family of Heavy top problem with a general solution uniform over the whole complex time plane are the four integrable cases(see[2]).In this way Liapounov improved the Kowalevskaya’s result,he considered for the fi rst time the Poincar´e’s variational equation of the concerned system,with respect to the initial conditions,in the complex time along a suitable particular solution.In 1982,Ziglin[17]got a non-integrability result for complex analytical Hamiltonian systems by using the constrains imposed by the existence of some fi rst integrals on the monodromy group of the normal variational equation along some complex integral curve.This idea was later developed by Morales-Ruizet al.[18–19]and Baideret al.[20]in the end of the last century.By using the di ff erential Galois theory and investigating the relation of the integrability and the structure of the identity component of the di ff erential Galois group of the variational equation along some complex integral curve,they obtained a stronger integrability condition for Hamiltonian systems,the corresponding method and results are usually called Morales-Ramis theory.So far,many developments and applications of di ff erential Galois theory to the integrability have been obtain in numerous references and reports,such as[18–19,21–25]and so on.

In the present paper,we fi rstly investigate the connection between the Painlev´e property and the integrability of polynomial dynamical systems,and beyond the known results,we get the existence of certain class of integrals in the assumption of Painlev´e property,we also investigate the connection between the Painlev´e property of polynomial dynamical systems and the structure of the di ff erential Galois group of the corresponding variational equations along some complex integral curve.

The structure of this paper is as follows.In Section 2,we fi rstly recall the preliminary procedure and some results of Painlev´e analysis,and the relationships between the Painlev´eproperty and the integrability of polynomial dynamical systems be considered.In Section 3,several results are given after a short review of di ff erential Galois theory.We give some discussion of our results in the last section.

2 Painlev´e Property and Integrability

Consider a system of di ff erential equation

where x∈Cn,t∈Cand each component of f is polynomial in x.We say that(2.1)has Painlev´e property if the general solution of(2.1)has no movable critical singularity,i.e.,the general solution is single-valued in the complex plain.

Let

where p1,p2,q1,q2∈Z,α is a parameter,a and all components of b are constants.By a convenient choice of p1,p2,q1,q2,(2.1)is changed into

Expand the general solution X of(2.2)as follows:

The following result is crucial for Painlev´e analysis(see[26]).

Theorem 2.1(Painlev´e’s α-lemma)LetF(X;T;α)be analytic in a path-connected domain(X,T,α)∈DX×DT×Dα⊂Cn×C×C.For a given initial condition(X(T0),T0)∈DX×DTandϵ∈R+sufficiently small,the general solution of(2.1)is single-valued for allαsuch that|α|＜ϵif and only ifXi(T)is single-valued for alliandXiis de fi ned in(2.3).

Assume that there exists a decomposition with m+1 weight-homogeneous components such that the dominant part of vector fi eld f(0)is a scale system,i.e.,the system

has the exact scale-invariant solution

where τ=t−t∗,p∈Qn,ξ∈Cn,|ξ|≠0,t∗is an arbitrary movable singularity.Then, there exist q(1),···,q(m)∈Qwith 0＜q(i)＜q(j)(i＜j)such that

Here,we call the pair(ξ,p)a dominator balance(or balance)for the vector fi eld(2.1),and denote all balances satisfying above conditions by F.

For a given balance(ξ,p)∈F,rewrite the general solution of the system(2.5)around ξτpas

then we have

where

is called Kowalevskaya matrix,whose eigenvalues are called Kowalevskaya exponents,

Theorem 2.2(Painlev´e’s test#1)Suppose that(2.1)has Painlev´e property.Then,for any balance(ξ,p)∈F,all the dominant exponentsp1,···,pnare integers,the Kowalevskaya matrixKis semi-simple and Kowalevskaya exponentsλ1,···,λnareintegers.

Now,we make the change of variables

then(2.1)becomes

where

where

“′”is the di ff erentiation with respect to s,

and

在作业划分的过程中也需要讲究正确的方法，如果作业划分的过于粗糙会导致作业成本管理工作的开展受到阻碍。但是如果划分的过于精细则会无形中扩大成本的核算量，不仅大大增加了工作量，同时也会影响成本核算的进度。所以在实际的应用过程中，必须要站在机场企业的价值链角度思考，对作业进行科学的划分。

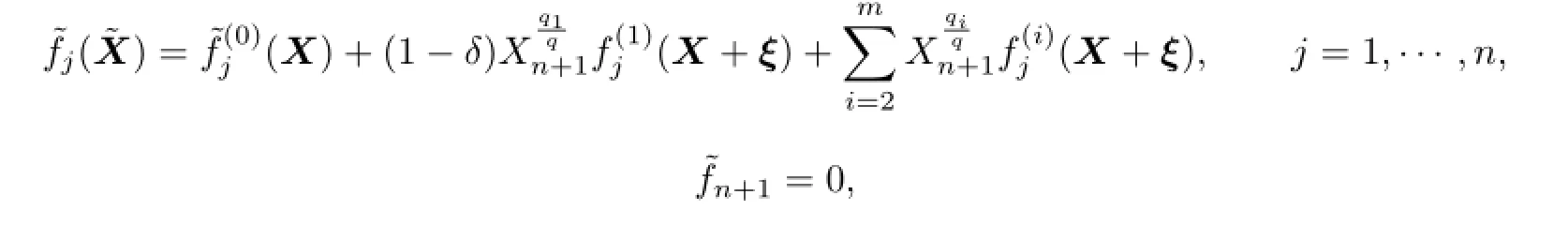
where

It is not difficult to know that the eigenvalues of˜K are Λ={λ1,···,λn,λn+1}with λn+1=q,and

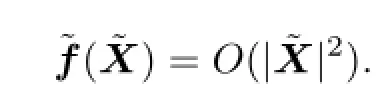
Note that if K is semi-simple,so isWithout loss of generality,we assume that=diag(Λ).Then,it is easy to obtain that,around the original point,the local formal solution of(2.8)can be represented as

where Ci(s)are polynomial valued vector with respect to s,a=(a1,···,an,an+1)are free parameters,··and〈Λ,i〉=Then,one can conclude easily that the local solution of(2.1)around the singularity t∗can be represented as

where an+1=1,is the n-dimensional vector obtained by the fi rst n components of Ci(s).

Theorem 2.3(Painlev´e’s test#2,3)Suppose that(2.1)has Painlev´e property.Then,for any balance(ξ,p)∈F,all the dominant exponentsp1,···,pnare integers,the Kowalevskaya matrixKis semi-simple and Kowalevskaya exponentsλ1,···,λnare integers,and the local solution can be represented as formal Laurent series

withn−1arbitrary constants,whereBiare constant valued vectors.Furthermore,(2.1)has local Laurent solution

with as many arbitrary constants as the number of positive Kowalevskaya exponents.

From above observations,one can fi nd that for a system with Painlev´e property,there exist several constants corresponding to its local formal solution.These constants always imply certain integrability of the considered system.In fact,we have the following result.

Theorem 2.4Suppose that(2.1)has Painlev´e property,and the balance setF∅. Then(2.1)is local formal integrable,i.e.,there existnfunctionally independent fi rst integralsI1(x,t),···,In(x,t)which are analytic with respect toxandt1lfor somel∈Z+. Furthermore,if there exists a balance(ξ,p)∈Fsuch that Kowalevskaya exponentsλ1,···,λn−1are positive integers,then(2.1)hasnfunctionally independent local convergence fi rst integralsI1(x,t),···,In(x,t)which are analytic with respect toxandt1lfor somel∈Z+.

Proof.If(2.1)has Painlev´e property,then,by Theorem 2.3,the coefficients of the general solution of the autonomous(2.8)are constants,that is to say,there exists a formal nonsingular transformation of variables

such that(2.8)becomes

It is easy to see that they are formal Laurent series with respect to x and tq,and they are independent and invariant along any solution of(2.1),i.e.,they are fi rst integrals of the system(2.1).The proof is completed.

Furthermore,if there exists a balance(ξ,p)∈F such that Kowalevskaya exponents λ1, ···,λn−1are positive integers.Then we can conclude from[13]and above arguments,the corresponding local solution(2.10)and(2.9)are local convergent,therefore,the transformation(2.11)is local analytic,and hence I1(x,t),···,In(x,t)are local convergent fi rst integrals of(2.1).

One can also fi nd that having Painlev´e property always implies well structure(regular property)of general solution as well as the linear equation obtained from the variation of considered system along the corresponding invariant solution.In what follows,we are going to make these investigations.Before this,let us recall some basic notions and results about di ff erential Galois theory.

3 Painlev´e Property and Di ff erential Galoisian Theory

The di ff erential Galois theory,or Picard-Vessiot theory is an e ff ective tool to study the solvability of homogeneous linear di ff erential equations.The main idea of it is to link the Liouwille integrability of equations with the structure of corresponding di ff erential Galois group.Here we only review some basic notions and results as in[24],for more details,see [27].

A di ff erential fi eld is a pair(K,∂)consisting a fi eld K and a derivative∂,which is an additive mapping∂:K→K satisfying

The constants are the elements of the sub fi eld Const(K):=ker∂of K.Usually,we write a′(resp.a(n))instead of∂(a)(resp.∂(n)(a)).We also use this notation for elements of Knand Mat(K,n),extending the derivation entry wise,here Mat(K,n)is the set of n×n matrices with entries in K.An extension of di ff erential fi elds,usually denoted by L|K,is an inclusion L⊃vK,such that∂L|K=∂K,here∂L,∂Kare the derivation of L,K,respectively.Given a linear homogeneous di ff erential system on di ff erential fi eld(K,∂)

First,we refer the two of the basic notions,i.e.,Picard-Vessiot extension and di ff erential Galois group corresponding to it.

De fi nition 3.1L|Kis a Picard-Vessiot(P-V)extension for(3.1)if

(1)Const(L)=Const(K);

(2)there exists a fundamental matrixΦ∈GL(L,n)for(3.1);

(3)Lis generated overKas a di ff erential fi eld by the entries ofΦ.

We assume that the constant sub fi eld of di ff erential fi eld(K,∂)is characteristic zero, and just for simplicity,Const(K)=C.Then the P-V extension of(3.1)exists and is unique in sense of isomorphism of di ff erential fi elds.

De fi nition 3.2IfL|Kis a P-V extension for(3.1),then all di ff erentialK-automorphisms(σ:L→ L,σ(a′)=(σ(a))′,a∈Landσ(a)=a,a∈K)ofLis called the di ff erential Galois group ofLoverK(or of(3.1))and denoted byGal(L/K)or also by

The di ff erential Galois group of(3.1)is a linear algebraic subgroup of GL(C,n),i.e.,its elements are matrices whose coefficients are zeros of some polynomials inC.Indeed,given a fundamental matrix Φ∈GL(L,n),and σ∈Gal(L/K),σ(Φ)is also a fundamental matrix of(3.1),hence σ(Φ)=ΦM(σ)with M(σ)∈GL(C,n),which yields an n-dimensional faithful representation

which renders that Gal(L/K)is a linear group,for further proof it being algebraic group, see[27].Based on the above fact,whenever G is the di ff erential Galois group of some P-V extension,we are identifying elements σ of G with the corresponding matrices M(σ)de fi ning representation in(3.2).In other words,we are dealing either with the linear algebraic group G or the matrix group ρ(G).

We remark that,in fact,the above two notions can be introduced without concerning the concrete di ff erential equations,for more details,see[28].However,here we shall consider the solvability of linear homogeneous equations as the form of(3.1),therefore we should not only introduce above notions,but also the following Liouvillian integrability due to Liouville.

De fi nition 3.3LetKbe a di ff erential fi eld.L|Kis a Liouvillian extension if no new constants are added and there exists a tower of extensions

such that fori=1,···,m,Li=Li−1(ai),and one of the following holds:

(2)ai̸=0and∈Li−1,in such case,aiis called an exponential integral(of an element ofLi−1);

(3)aiis algebraic overLi−1.

IfLis a Liouvillian extension ofKand allaiare integrals(resp.exponential integrals),we sayLis an extension by integrals(resp.exponentials)ofK.

De fi nition 3.4(3.1)is integrable(in Liouvillian sense)if one of its P-V extension is also a Liouvillian extension.

Just as the classical Galois theory on polynomial equations concerning the relation between the solvability of the polynomial equation and the solvability of the corresponding Galois group,one of the fundamental results of di ff erential Galois theory for linear system as follows.

Theorem 3.1LetL|Kbe a P-V extension for(3.1).Then the following statements are equivalent:

(1)(3.1)is integrable;

(2)the identity componentGal(L/K)0of di ff erential Galois groupGal(L/K)is solvable.

It is easy to see that if a P-V extension is de fi ned only by quadrature adjunction

where f1,f2,···,fk∈K,then its Galois group Gal(L/K)is equal to(C+)s,s≤k,whereC+denotes the additive group ofC.Furthermore,the identity component of Gal(L/K)is equal to itself,i.e.,the Galois group is connected.

Based on above preparations,we now give our second result.

Theorem 3.2Suppose that(2.1)has Painlev´e property.Then for any balance(ξ,p)∈F,the identity component of Galois group of thekth order variational equations of the weight homogeneous equation(2.5)along its scale-invariant solutionτpξis trivial fork=1,abelian fork=2,and solvable fork∈Z+/{1,2}.Furthermore,if there exists a balance(˜ξ,˜p)∈Fsuch that(2.1)has a local solution expressed as a local convergent Laurent form

then the identity component of Galois group of thekth order variational equations of(2.1)along(3.3)is abelian fork=1,and solvable fork∈Z+/{1}.

Proof.It is well known that if(2.1)has Painlevproperty,so does(2.5),then the general solution of(2.5)must be single-valued.Consider the variational equations of(2.5)along the solution τpξ,

where F1≡0.Note that the identity components of the Galois groups of(3.4)and(3.5) are the same.By Theorem 2.3,we have that K is semi-simple,and all its eigenvalues are integers.So the general solution of the fi rst variational equation is rational function.Therefore the di ff erential Galois group of the fi rst variational equation is trivial.Further,it is easy to see that the general solutions of other higher order variational equations can be obtained by a fi nite Liouville extension(by integrals)of the rational di ff erential functional f i eld,which implies that the identity component of Galois group of the kth order variational equation is abelian for k=2,and solvable for k∈Z+/{1,2}.

Furthermore,if there exists a balance∈F such that(2.1)has a local solution (3.3),then with the change of variables x(k)→k=1,2,···,the kth order variational equations of(2.1)along(3.3)are transformed into

where Ai,i=1,2,···,are constant matrices,and≡0.With the same arguments as above,K is semi-simple,and all its eigenvalues are integers,therefore the fundamental solution matrix of(3.6)for k=1 can be locally expressed as X(1)=P(τ)τˇK,where P(τ)is local analytic andˇK is a constant matrix whose eigenvalues are all the same and integers.Then the identity component of local di ff erential Galois group of the fi rst order variational equation of(2.1)along(3.3)is abelian.Since the general solutions of other higher order variational equations can be obtained by a fi nite Liouville extension of the rational di ff erential functional fi eld,we get that the identity component of Galois group of the kth order variational equation is also solvable for k∈Z+.

4 Discussions

In the above sections,we consider some connections between the Painlev´e property and integrability of polynomial dynamical systems.We mainly consider the existence of certain class of integrals in the assumption of Painlev´e property.The kinds of the fi rst integrals that we have obtained are,however,not so nice in general,which may be due to the fact that the convergence property of the integrals is related to the sign of the Kowalevskaya exponents.Further,we think that,in order to make a system integrable with nice(analytic for example)integrals,more conditions should be added beside the Painlev´e property.

Example 4.1Consider the PainlevII equation:

It can be viewed as the following autonomous system:

which has a decomposition

with a balance

where

By a direct calculation,we obtain that the correspondence Kowalevskaya exponents are {−1,−1,4}.By Theorem 2.3,(4.2)has a convergent solution with at most one free parameter.Then by Theorem 2.4,we conclude that only one of the fi rst integrals is convergent, which implies that(4.1),and therefore the Painlev´e II equation,is non-integrable.In fact, it has been proved that(4.1)is non-integrable forµ∈Z+in[29].

We also consider the connection between the Painlev´e property of general dynamical systems and the structure of the di ff erential Galois group of the corresponding variational equation along some complex integral curve.The results we have gotten are,in fact,the necessary conditions of the Painlev´e property,and it is not difficult to see that,these necessary conditions are almost the same as the ones in[21]and the Morales-Ramis theory.

[1]Kowalevskaya S.Sur le probleme de la rotation d’un corps solide autour d’un point fi xe(in French).Acta Math.,1889,12:177–232.

[2]Lyapounov A M.On a certain property of the di ff erential equations of the problem of motion of a heavy rigid body having a fi xed point.Soobshch.Kharkov Math.Obshch,Ser.2,1894,4: 120–140.

[3]Adler M,Van Moerbeke P.The complex geometry of the Kowalevski-Painlev´e analysis.Invent. Math.,1989,97:3–51.

[4]Goriely A.Investigation of Painlev´e property under time singularities transformations.J.Math. Phys.,1992,3(8):2728–2742.

[5]Goriely A.Integrability,patial integrability and nonintegrability for systems of orsdinary differential equaitons.J.Math.Phys.,1996,37:1871–1893.

[6]Goriely A.Painlev´e analysis and normal form.Phys.D,2001,152,124–144.

[7]Kruskal M D,Ramani A,Grammaticos B.Singularity and Its Relation to Complete,Partial and Non-integrability.Partially Integrable Evlotion Equations in Physics.Dordrechr:Kluwer Academic Publishers,1990:321–372.

[8]Ramani A,Grammaticos B.The Painlev´e property and singularity analysis of integrable and non-integrable systems.Physics Reports,1989,180:159–245.

[9]Ramani A,Dorizzi B,Grammaticos B,Bountis T.Integrability and the Painlev´e property for low-dimensional systems.J.Math.Phys.,1984,25:878–883.

[10]Ra˜nada A F,Ramani A,Dorizzi B,Grammaticos B.The weak-Painlev´e property as a criterion for the integrability of dynamical systems.J.Math.Phys.,1985,26:708–710.

[11]Yoshida H.Necessary condition for the non-existence of algebraic fi rst integral I,II.Celestial Mech.,1983,31:363–379,381–399.

[12]Yoshida H.A Criterion for non-existence of an additional integral in Hamiltonian systems with a homogeneous potential.Phys.D,1987,29:128–142.

[13]Goriely A.Integrability and Non-integrability of Dynamical Systems.Singapore:World Scienti fi c Publishing Co.,2001.

[14]Liu F,Shi S Y,Xu Z G.Nonexistence of formal fi rst integrals for general nonlinear systems under resonance.J.Math.Anal.Appl.,2010,363:214–219.

[15]Shi S,Li Y.Non-integrability for general nonlinear systems.Z.Angew.Math.Phys.,2001,52: 191–200.

[16]Shi S.On the nonexistence of rational fi rst integrals for nonlinear systems and semiquasihomogeneous systems.J.Math.Anal.Appl.,2007,335:125–134.

[17]Ziglin S L.Branching of solutions and non-existence of fi rst integrals in Hamiltonian mechanics I.Funct.Anal.Appl.,1983,16:6–17.

[18]Morales-Ruiz J J.Di ff erencial Galois Theory and Non-integrability of Hamiltonian Systems. Berlin:Birkh¨auser,1999.

[19]Morales-Ruiz J J,Sim´o C.Picard-Vessiot theory and Ziglin’s theory.J.Di ff erential Equations, 1994,107:140–162.

[20]Baider A,Churchill R C,Rod D L,Singer M F.On the in fi nitesimal geometry of integrable systems.Fields Inst.Commun.,1996,7:5–56.

[21]Li W L,Shi S Y.Galoisian obstruction to the integrability of general dynamical systems.J. Di ff erential Equations,2012,252:5518–5534.

[22]Maciejewski A J,Przybylska M.All meromorphically integrable 2D Hamiltonian systems with homogeneous potential of degree 3.Phys.Lett.A,2004,327:461–473.

[23]Morales-Ruiz J J,Sim´o C.Non-integrability criteria for Hamiltonians in the case of Lam´e normal variational equations.J.Di ff erential Equations,1996,129:111–135.

[24]Morales Ruiz J J.A remark about the Painlev´e transcendents.S´eminaires.Congr´es.,2006,14:229–235.

[25]Tsygvintsev A.The meromorphic nonintegrability of the three-body problem.C.R.Acad.Sci. Paris S´er.I Math.,2000,331:241–244.

[26]Kruskal M D,Clarkson P A.The Painlev´e-Kowalevski and poly-Painlev´e test for integrability. Stud.Appl.Math.,1992,62:87–165.

[27]Van der Put M,Singer M F.Galois Theory of Linear Di ff erential Equations.Vol.328. Grundlehren der Mathematischen Wissenshaften.Heidelberg:Springer,2003.

[28]Magid A R.Lecture on di ff erential Galois theory.Providence,Rhode Island:American Mathematical Society,1994.

[29]Morales-Ruiz J J,Ramis J P,Sim´o C.Integrability of Hamiltonian systems and di ff erential Galois groups of higher variational equations.Ann.Sci.´Ecole Norm.Sup.(4),2007,40:845–884.

tion:34C14,37F75,34M15,32M25

A

1674-5647(2014)04-0358-11

10.13447/j.1674-5647.2014.04.09

Received date:April 15,2014.

Foundation item:The NSF(11371166,11301210)of China,National 973 Project(2012CB821200)of China, and Jilin Province Youth Science Foundation.

*Corresponding author.

E-mail address:lwlei@jlu.edu.cn(Li W L),shisy@jlu.edu.cn(Shi S Y).