Statistical Inference for the Parameter of Pareto Distribution Based on Progressively Type-I Interval Censored Sample

ABDALROOF M.S.,ZHAO ZHI-WEN2,*AND WANG DE-HUI

(1.College of Mathematics,Jilin University,Changchun,130012)

(2.College of Mathematics,Jilin Normal University,Siping,Jilin,136000)

Statistical Inference for the Parameter of Pareto Distribution Based on Progressively Type-I Interval Censored Sample

ABDALROOF M.S.1,ZHAO ZHI-WEN2,*AND WANG DE-HUI1

(1.College of Mathematics,Jilin University,Changchun,130012)

(2.College of Mathematics,Jilin Normal University,Siping,Jilin,136000)

In this paper,the estimation of parameters based on a progressively type-I interval censored sample from a Pareto distribution is studied.Di ff erent methods of estimation are discussed,which include mid-point approximation estimator,the maximum likelihood estimator and moment estimator.The estimation procedures are discussed in details and compared via Monte Carlo simulations in terms of their biases.

EM-algorithm,maximum likelihood estimation,method of moment, Bayes estimation

1 Introduction

A useful and tractable parametric model with relatively high probability in the upper tail is the Pareto distribution f(y;α,θ)having probability density function

and cumulative distribution function

where α＞0 and θ＞0 are unknown parameters.Here we treat estimation of the shape parameter α that characterizes the tail,with the scale parameter θ assumed known.That is,we consider(1.1)as a single-parameter Pareto model,following[1–2].In actuarial applications,(1.1)with θ known is appropriate when losses or claims below a certain levelare not relevant(for example,when a deductible applies).In such a case,θ can represent the deductible,or sometimes a lesser value in order to incorporate in fl ation into the model, while ignoring data irrelevant to the issues under study.The parameter α,on which we focus,plays a key role in connection with determination of extreme quantiles,upper tail probabilities,mean excess functions,and excess-of-loss and stop-loss reinsurance premiums. For general overviews of the role of Pareto distribution and variants in actuarial science, econometrics,and other fi elds,see[3–4].New application contexts continue to arise.For example,the cost distributions of combinatorial search algorithms have recently been shown to exhibit Pareto-type tail behavior(see[5]).

Inferences for the Pareto distribution were discussed by several authors.In case the data are complete,the maximum likelihood estimators(MLE)of α and θ are easy to calculate,and Quandt[6]proved that the MLEˆα andˆθ are consistent with the parameters α and θ,respectively.But it is complicated to compute MLE for censored data.Cohen and Whitten[7]proposed a moment estimator(ME)to estimate the parameters of Pareto distribution.Moreover,Geisser[8]has provided extensive analysis of the application of Bayesian methods in predicting the future values of this distribution of random variables from observed values in a complete random sample.Nigm and Hamdy[9]have also considered a similar problem under censored data.Pandeyet al.[10]obtained the Bayesian estimator of the shape parameter using LINEX loss function.Wu[11]considered the maximum likelihood estimation problem based on progressive type-II censoring with random removals, and constructed the con fi dence intervals for the parameters and percentile of the lifetime distribution.Recently,Huang[12]has proposed an optimal estimation method for the shape parameter,probability density function and upper tail probability of the Pareto distribution based on a weighted empirical distribution function.In this article,we discuss the estimation of parameters based on a progressively type-I interval censored sample from the Pareto distribution.

In many life-testing and reliability studies,experimental units can be removed progressively from the experiment in di ff erent stages of the testing.The major reasons for removal of the experimental units are saving the working experimental units for future use,reducing the total time on test and lowering the cost.Data obtained from such experiments are called progressive censored data.Aggarwala[13]explored a union of type-I interval and progressive censoring and developed the statistical inference for exponential distribution for progressive type-I interval censored sample.Since then,statistical analysis for progressive type-I interval censored data has been studied by many authors(see[14–16]).

Progressive type-I interval censoring scheme can be described as follows.Consider n units which put on a test at time t0=0.The units are inspected at m preci fi ed times t1,t2,···,tm,where tmis the scheduled time to terminate the experiment.At the ith inspection time ti,the number Xiof failures within(ti−1,ti]is recorded and Risurviving items are randomly removed from the life testing,for i=1,2,···,m.As the numbers of surviving units at times t1,t2,···,tm,are random variables,the numbers of removal R1,···, Rmcan be determinated as pre-speci fi ed percentages of the remaining surviving units.Forexample,given pre-speci fi ed percentage values,p1,···,pm−1and pm=1,for withdrawing at t1＜t2＜···＜tm,respectively,Ri=[piyi]at each inspection time ti,where[piyi] denotes the largest integer which is smaller than or equal to piyi.In this paper,we give the mid-point approximation estimate,maximum likelihood estimate and moment estimate of the shape parameter α in Pareto distribution based on progressive type-I interval censoring sample.

The rest of this article is organized as follows.In Section 2,we describe the speci fi c estimate procedure of the above estimate methods.Simulation results are provided in Section 3.

2 Parameter Estimation

2.1 Mid-point Approximation Method

In this section,we provide the mid-point approximation estimator of the unknown parameter α.

First,suppose that the exact failure times of the n units on test are known and denoted as y1,y2,···,yn.Then the likelihood function is given by

The corresponding log-likelihood functions are

Taking derivatives with respect to α in(2.1)and equating them to zero,we obtain the likelihood equation

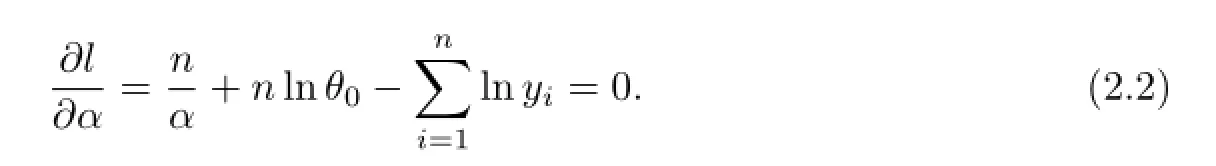
From(2.2),we obtain

with l=1,2,···,n;i=1,2,···,m.

Then we have a progressive type-I censored sample.Similarly,the likelihood function is given by

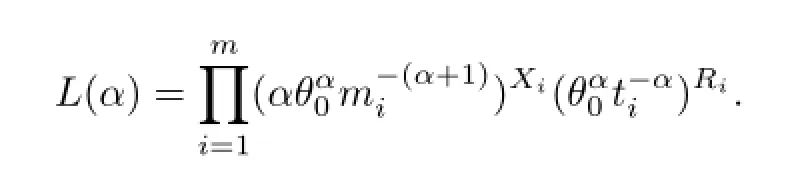
The corresponding log-likelihood function is obtained as

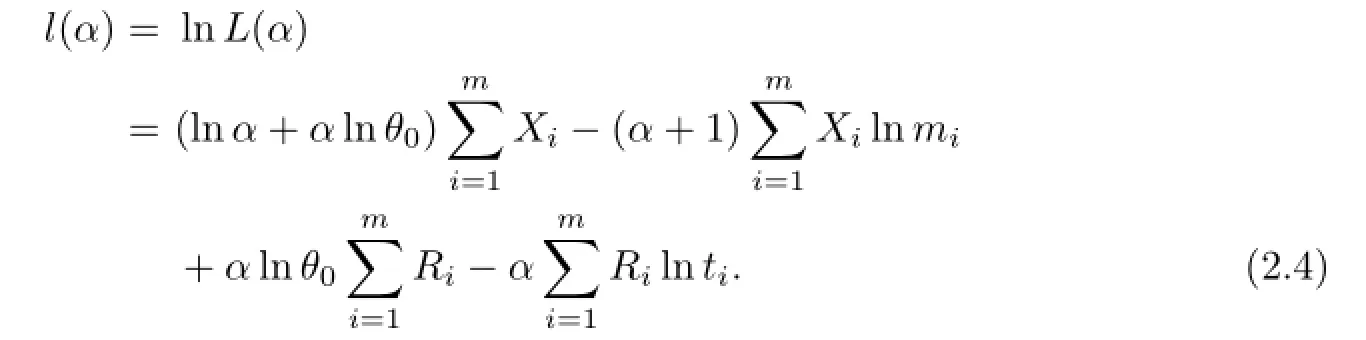
Taking derivatives with respect to α in(2.4)and equating them to zero,we obtain the likelihood equation as

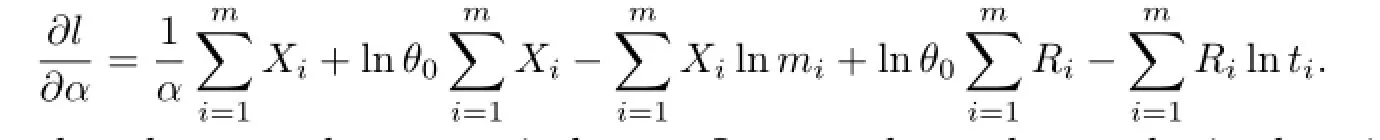
Therefore,based on pseudo progressively type-I censored sample,we obtain the mid-point estimator(denoted by MPP)

2.2 Maximum Likelihood Estimation

In this section,we consider the maximum likelihood estimator(MLE)of the parameter α based on progressive type-I interval censored sample.The likelihood function is

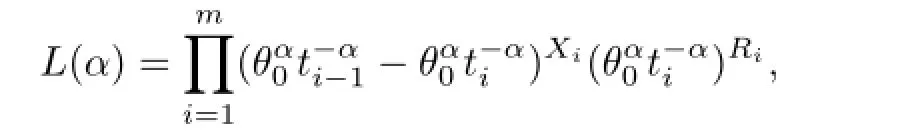
and the log-likelihood function is

Taking derivatives with respect to α in(2.5)and equating them to zero,we obtain the likelihood equation

Here,we use the EM-algorithm(see[17])to obtain the MLE.The lifetimes of the Xifailures in the ith interval(ti−1,ti]are independent and follow a doubly truncated Rayleigh distribution from the left at ti−1and from the right at ti,and the lifetimes of the Ricensored items in the ith interval(ti−1,ti]are independent and follow a truncated Rayleigh distribution from the left at ti,i=1,2,···,m.The required expected value of a doublytruncated Rayleigh distribution from the left at a and from the right at b with 0＜a＜b＜∞for EM-algorithm is given by

and

The concise procedure of the EM-algorithm is as follows:

1.Given an initial estimate of α(for example,the aforementioned mid-point approximation estimator),say α(0).

2.In the hth iteration,the E-step requires to compute

and

3.The M-step maximizes the likelihood function.Based on the likelihood equation for complete data,we can obtain the estimate

4.Setting h=h+1,the MLE of α can be obtained by repeating the E-step and M-step until convergence occurs.

2.3 Method of Moments

After simple algebraic manipulation,we obtain that,for α＞δ,

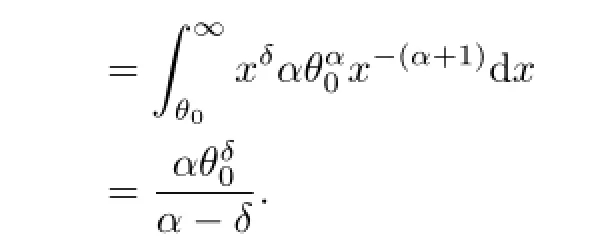
By equating the sample moment to the corresponding population moment,we have the following equation:

Iterative procedure can be employed to solve the above equations for α as follows.

1.Given an initial estimate of α(the mid-point approximation estimator described can be used as an initial value here),say α(0).

2.Starting from h=0,in the(h+1)th iteration,we fi rst compute Eα(Yδ|Y∈[ti−1,ti)) and Eα(Yδ|Y∈[ti,∞)).

3.Based on(2.6),we have

4.Setting h=h+1,repeating steps 2 and 4 until convergence occurs and denoting the method of moment estimator(MME)asˆαM.

3 Simulation Study

Monte Carlo simulation is used to study the performance of all the estimators proposed in Section 2.We take θ0=0.8,1.0,1.2,α=0.4,0.5,0.8,1.0,1.3,1.5,2.0.We consider the situations with small sample size(n=100),moderate sample size(n=300)and large size(n=1000).Following the simulation algorithm presented by Aggarwala[13],we simulate progressive type-I interval censored data with fi ve inspection/censoring points,i.e.,

The following censoring schemes(c.s.),which specify the proportions of surviving units to be removed at the fi ve inspection points,are considered:

For each estimator,this procedure is repeated on 1000 samples,from which the mean values of the absolute value of biases are presented in Tables 3.1–3.12.

Now,we look at the performance of the estimators.In general,MPP gives the smallest biases in all cases and MPC has the highest biases.Moreover,as samples increase,the biases of MPP decrease.It is worth mentioning that the censoring schemes p3and p4have a larger proportion of surviving units to be removed at the fi rst two inspection points.Therefore,in order to decrease cost,we can use the censoring schemes p3and p4.

Table 3.1 The mean values of the absolute value of biases

Table 3.2 The mean values of the absolute value of biases

Table 3.3 The mean values of the absolute value of biases

Table 3.4 The mean values of the absolute value of biases

Table 3.5 The mean values of the absolute value of biases

Table 3.6 The mean values of the absolute value of biases

Table 3.7 The mean values of the absolute value of biases

Table 3.8 The mean values of the absolute value of biases

Table 3.9 The mean values of the absolute value of biases

Table 3.10 The mean values of the absolute value of biases

Table 3.11 The mean values of the absolute value of biases

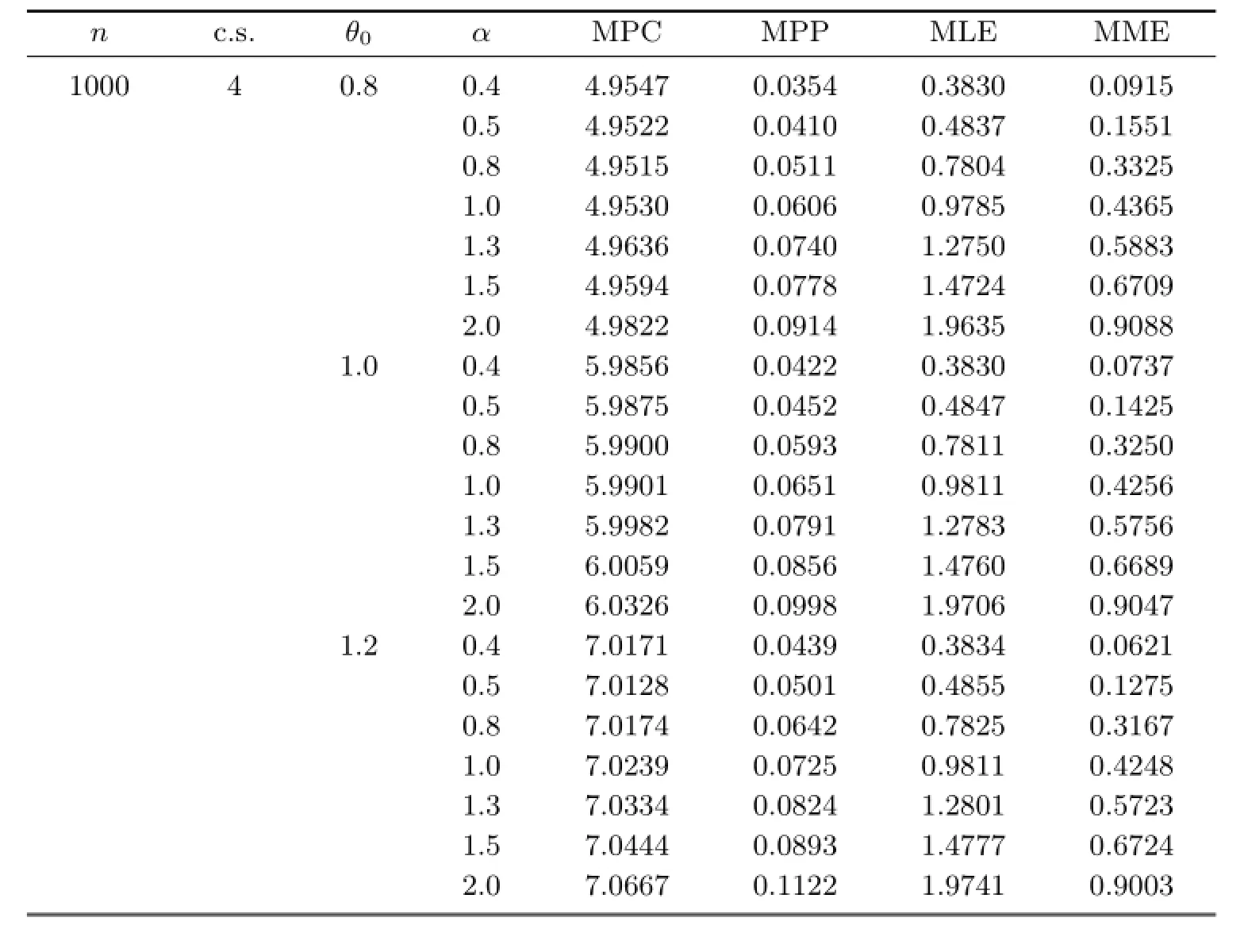
Table 3.12 The mean values of the absolute value of biases

[1]Beirlant J,Teugels J F,Vynckier P.Practical Analysis of Extreme Values.Leuven:Leuven Univ.Press,1996.

[2]Klugman S A,Panjer H H,Willmot G E.Loss Models:From Data to Decisions.New York: Wiley,1998.

[3]Arnold B C.Pareto Distributions.Fairland:International Cooperative Publishing House,1983.

[4]Johnson N L,Kotz S,Balakrishnan N.Continuous Univariate Distributions.New York:Wiley, 1994.

[5]Gomes C P,Selman B,Crato N.Heavy-Tailed Distributions in Combinatorial Search.in: Smolka G.Principles and Practice of Constraint Programming CP-97.Berlin:Springer,1997: 121–135.

[6]Quandt R E.Old and new methods of estimation and the Pareto distribution.Metrika,1966,10:55–82.

[7]Cohen A C,Whitten B J.Parameter Estimation in Reliability and Life Span Models.New York:Marcel Dekker,1988.

[8]Geisser S.Interval prediction for Pareto and exponential observables.J.Econometrics,1985,29:173–185.

[9]Nigm A M,Hamdy H I.Bayesian prediction bounds for the Pareto lifetime model.Comm. Statist.Theory Methods,1987,16:1761–1772.

[10]Pandey B N,Singh B P,Mishra C S.Bayes estimation of shape parameter of classical Pareto distribution under livex loss function.Comm.Statist.Theory Methods,1996,25:3125–3145.

[11]Wu S J.Estimation for the two-parameter Pareto distribution under progressive censoring with uniform removals.J.Statist.Comput.Simulation,2003,73:125–134.

[12]Huang M L.Optimal estimation for the Pareto distribution.J.Statist.Comput.Simulation, 2011,81:2059–2076.

[13]Aggarwala R.Progressively interval censoring:some mathematical results with application to inference.Comm.Statist.Theory Methods,2001,30:1921–1935.

[14]Chen D G,Lio Y L.Parameter estimations for generalized exponential distribution under progressive type-I interval censoring.Comput.Statist.Data.Anal.,2010,54:1581–1591.

[15]Lin C T,Wu Sam J S,Balakrishnan N.Planning life tests with progressively type-I interval censored data from the lognormal distribution.J.Statist.Plann.Inference,2009,139:54–61.

[16]Yan W,Shi Y,Song B,Mao Z.Statistical analysis of generalized exponential distribution under progressive censoring with binomial removals.J.Systems Engrg.Electron.,2011,22: 707–714.

[17]Dempster A P,Laird N M,Rubin D B.Maximum Likelihood from incomplete data via the em algorithm.J.Roy.Statist.Soc.Ser.B,1977,39:1–38.

tion:62F15,62F10

A

1674-5647(2014)04-0345-13

10.13447/j.1674-5647.2014.04.08

Received date:May 4,2012.

Foundation item:The NSF(11271155,11001105,11071126,10926156 and 11071269)of China,the Specialized Research Fund(20110061110003 and 20090061120037)for the Doctoral Program of Higher Education,the General Humanities and Social Science Research Projects(11YJAZH125)Sponsored by Ministry of Education,the Science and Technology Development Program(201201082)of Jilin Province.

*Corresponding author.

E-mail address:abdalroof1@gmail.com(Abdalroof M S),zhaozhiwen@126.com(Zhao Z W).