A Class of Metric Spaces Which Do Not Coarsely Contain Expanders

(Department of Mathematics,University of Puerto Rico,Rio Piedras Campus, San Juan,Puerto Rico,00923,USA)

A Class of Metric Spaces Which Do Not Coarsely Contain Expanders

SHAN LIN

(Department of Mathematics,University of Puerto Rico,Rio Piedras Campus, San Juan,Puerto Rico,00923,USA)

Communicated by Gong Gui-hua

In this paper,a class of metric spaces which include Hilbert spaces and Hadamard manifolds are de fi ned.And the expanders cannot be coarsely embedded into this class of metric spaces are proved.

coarse embedding,expander,special metric space

Let X,Y be two metric spaces.A map f∶X→Y is called a coarse embedding if there exist two non-decreasing functions ρ1,ρ2∶[0,∞)→[0,∞)such that

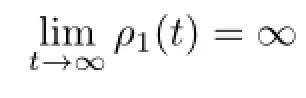
and

If X admits a coarse embedding into Y,then X is called coarsely embeddable into Y or Y coarsely contains X.

In[1],it was proven that the coarse Baum-Connes conjecture holds for spaces which admit a coarse embedding into Hilbert spaces.Similarly in[2–3],it was proven that the coarse geometric Novikov conjecture holds for spaces which admit a coarse embedding into Hadamard manifolds.On the other hand,it is also known that there exist spaces which cannot be coarsely embedded into either Hilbert spaces or Hadamard manifolds.The known construction of such coarsely non-embeddable spaces depends on expanders.

Let(V,E)be a fi nite graph with the vertex set V and the edge set E.We denote the cardinality of V and E by|V|and|E|,respectively.We also de fi ne an orientation on E.

The di ff erential d∶ℓ2(V)→ℓ2(E)is de fi ned by

with the starting vertex e+and the ending vertex e−.

The Laplace operator Δ=d⋆d,where d⋆is the adjoint operator of d.This de fi nition does not depend on the choice of the orientation of E.Apparently,Δ is self-adjoint.Also it is positive since〈Δf,f〉=〈df,df〉≥0.Hence Δ has real nonnegative eigenvalues.We denote λ1(V)the minimal positive eigenvalue of the Laplace operator Δ on the graph(V,E).

De fi nition 1A sequence of graphsof the fi xed degreeland with|Vn|approaching to∞is called anexpanderif there is a positive constantcsuch that≥cfor alln∈N+.The largest possiblecis called the Laplace constant of{(Vn,En)}

and

As we mentioned at the beginning,

Theorem 1An expander is not coarsely embeddable into Hilbert spaces and Hadamard manifolds.

The proofs of the coarse non-embeddability of expanders into Hilbert spaces and Hadamard manifolds are di ff erent from literature(cf.[4–6]).Here we de fi ne a property and unify the proof for both cases.Let={y∈X|d(x,y)＜R}.

De fi nition 2A metric spaceXis called special if there exists a family ofs-Lipschitz maps{fx∶X→H|x∈X},whereHis a Hilbert space andR,l＞0such that

Example 1Hilbert spaces and Hadamard manifolds are special.

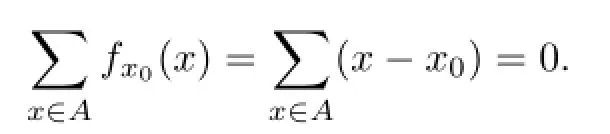
Clearly,it satis fi es all conditions with a choice L=K.

(2)For a Hadamard manifold M,we present Higson’s argument.This is the origin of the de fi nition of the special property.Assume that dimM=m.Let A be a fi nite subset ofM.By Hadamard theorem the exponential map expx∶TxM→M is a di ff eomorphism for every x∈M.And

Otherwise,let

Then the vector

Claim 1f is continuous.

Without loss of generality,we assume that A contains only one point a∈M.LetM→TxM be the parallel translation along the unique geodesic connecting x andon M.Then

Therefore,

Hence f is continuous.

Claim 2f is a retraction.

Let y∈S(∞).There exists a unique geodesic ray γ(t)with γ(0)=a and=y. Then

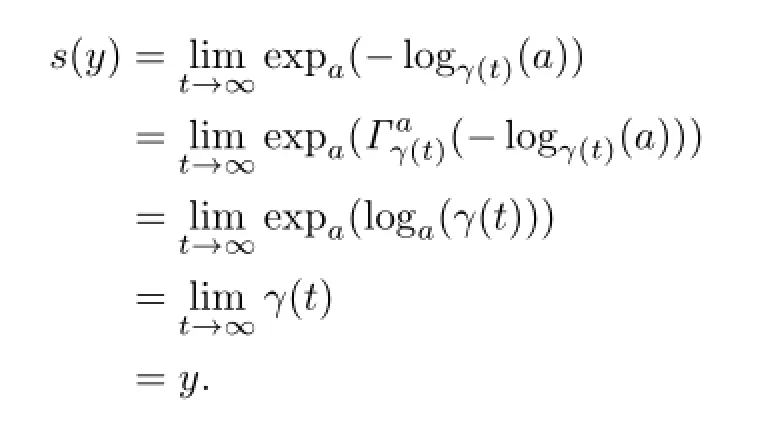
Therefore,f is a retraction as required.

Second,let K＞0.Then

where the last set is the K-ball in M.Then we choose L=K for the second condition.

To prove our main theorem,we recall a well-known concentration property of expanders.

Proposition 1Let{(Vn,En)}be an expander with the fi xed degreedand the Laplaceconstantc,andfn∶Vn→ Hbe a sequence ofs-Lipschitz maps to a Hilbert space.Iffor alln≥1,then

There are|Vn|summands on the left hand side of the above inequality.Therefore at leastsummands cannot exceed

Theorem 2An expander is not coarsely embeddable into a special metric space.

Proof.Let X be a special metric space in the above sense with constants R,l,s and a family of s-Lipschitz maps{fx∶X→H|x∈X},where H is a Hilbert space,with required properties.Assume thatis an expander with fi xed degree d and the Laplace constant c that is coarsely embedded into X.

This is fi nite because of the fi xed degree l of Vnfor all x∈N+.We have an estimate

This gives a contradiction with|Vn|approaching to∞.

It is natural to ask if ℓp(p＞2)is special.Mazur map might be helpful.But we do not know.Now let us make a detour.We modify the name of speciality above and call it“special with respect to Hilbert space”.Then we have the following generalized speciality.

De fi nition 3LetYbe a normed vector space andXbe a metric space.Xis called special with respect toYif there exists a family ofs-Lipschitz maps{fx∶X→Y|x∈X}andR,l＞0such that

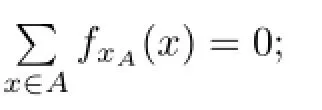
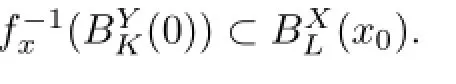
The following concentration theorem is crucial here.

Theorem 3[7]LetXbe a Banach space whose unit ball is uniformly embeddable into a Hilbert space.Then,for anyk∈N+andh＞0,there exists a positive numberR= R(k,h,X)which satis fi es the following statement∶

For any mapffrom a fi nite graphGwith fi xed degreekandλ1(G)＞hintoX,we havewheref(s)is the mean off.ℓp(p＞2)is a Banach space whose unit ball is uniformly embeddable into a Hilbert space.Therefore,combining Theorem 3,the fact that ℓpis special with respect to itself, and by the proof of Theorem 2,we have

Theorem 4An expander is not coarsely embeddable into a special metric space with respect to a Banach space whose unit ball is uniformly embeddable into a Hilbert space.and

Corollary 1An expander is not coarsely embeddable intoℓpwithp＞2.

[1]Yu G.The coarse Baum-Connes conjecture for spaces which admit a uniform embedding into Hilbert space.Invent.Math.,2000,139(1):201–240.

[2]Shan L.An equivariant higher index theory and non-positively curved manifolds.J.Funct. Anal.,2008,255:1480–1496.

[3]Shan L,Wang Q.The coarse geometric Novikov conjecture for subspaces of non-positively curved manifolds.J.Funct.Anal.,2007,248:448–471.

[4]Dranishnikov A N.Dimension theory local and global.Proceedings Nineteenth Annual Workshop in Geometric Topology,Hosted by Calvin College,June 13-15,2002,http://www.calvin.edu/～venema/workshop/proceedingspapers/dranishnikov.pdf.

[5]Nowak P,Yu G.Large Scale Geometry.EMS Textbook Math.Ser.,book draft.

[6]Shan L.A concentration theorem of expanders on Hadamard manifolds.J.Funct.Anal.,2012,263:109–114.

[7]Ozawa N.A note on non-amenability of B(ℓp)for p=1,2.Internat.J.Math.,2004,15: 557–565.

tion:46B99,58C99

A

1674-5647(2014)03-0284-05

10.13447/j.1674-5647.2014.03.10

Received date:Nov.1,2013.

E-mail address:lin.shan@upr.edu(Shan L).