One Nonparabolic End Theorem on K¨ahler Manifolds

(School of Mathematics and Physics,Jiangsu University of Technology, Changzhou,Jiangsu,213001)

One Nonparabolic End Theorem on K¨ahler Manifolds

ZHU PENG

(School of Mathematics and Physics,Jiangsu University of Technology, Changzhou,Jiangsu,213001)

Communicated by Yin Jing-xue

In this paper,the complete noncompact K¨ahler manifolds satisfying the weighted Poincar´e inequality are considered and one nonparabolic end theorem which generalizes Munteanu’s result is obtained.

nonparabolic end,weighted Poincar´e inequality,K¨ahler manifold

1 Introduction

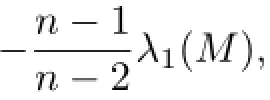
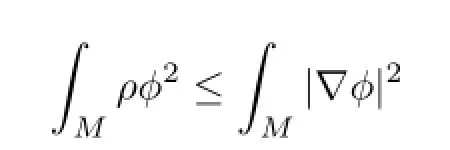
holds for all compactly supported piecewise smooth functionswhereare all compactly supported piecewise smooth functions on M.(M,ds2)is said to satisfy property(Pρ)if M satis fi es a weighted Poincar´e inequality with ρ and ρds2being complete. Obviously,the notion of the property(Pρ)is a generalization of λ1(M)＞0.Li and Wang considered a class of Riemannian manifolds of dimension n≥4 satisfying the property(Pρ) and having the Ricci curvature bounded below in terms of the weight function and gave arigidity theorem if ρ grows no more than exponential increase(see Theorem 5.2 in[3]).Later, Cheng and Zhou[4]obtained a result which generalized Theorem 5.2 in[3].Considering the manifolds satisfying property(Pρ)for a weight function ρ that has limit zero at in fi nity,i.e.,=0,Li and Wang[3]proved that for n≥4 and the Ricci curvature RicM(x)of M being bounded from below byfor each x∈M,the Riemannian manifold has only one nonparabolic end.In the setting of K¨ahler manifolds case,Munteanu[5]obtained analogous result to that for Riemannian manifolds,i.e.,a K¨ahler manifold M2n(n≥2)has only one nonparabolic end if the Ricci curvature RicM(x)of M is bounded from below by−4ρ(x)for each x∈M.

In this paper,the case of K¨ahler manifold is considered.Following the idea of Cheng and Zhou[4],a generalized theorem which contains the result of Munteanu[5]is obtained.More precisely,we have

Theorem 1.1LetMbe a complete noncompact real2n-dimensional K¨ahler manifold with property(Pρ)(n≥2).Suppose that the Ricci curvature ofMsatis fi es

where the non-negative bounded functionτ(x)satis fi es Poincar´e’s inequality

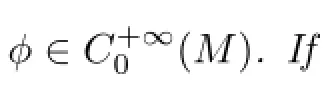
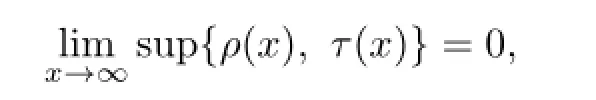
thenMhas only one nonparabolic end.

Remark 1.1If we choose τ=ρ in Theorem 1.1,then it is just Munteanu’s result,that is,Theorem 1 in[5].

2 Proof of the Main Result

Assume by absurd that M had at least two non parabolic ends,and thus there would exist a bounded harmonic function f with fi nite Dirichlet integral on M(see[6]).Moreover,we can assume that inf f=0 and supf=1 with in fi mum and supremum achieved at in fi nity of nonparabolic end E and F=ME,respectively.One has the improved Bochner formula for the function f∶

Lemma 2.1Letg=hφ(f)withφ∶(0,1)→(0,+∞)being aC∞function which is to be determined later.Then

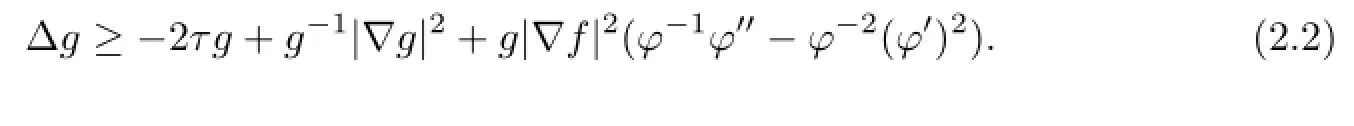
Proof.A direct computation shows that

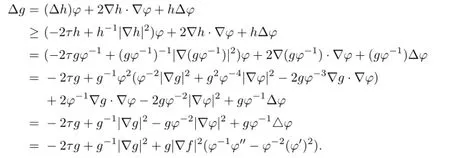
Lemma 2.2There exists the following inequality∶

Proof.Since

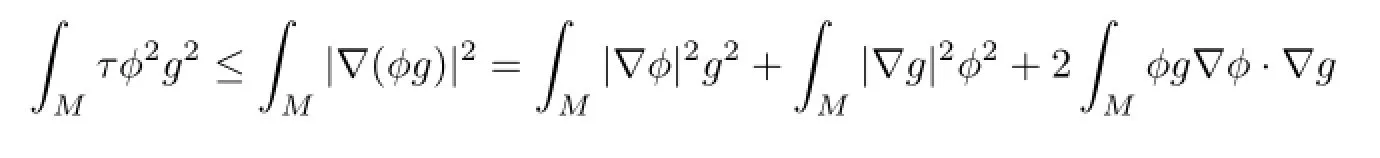
and

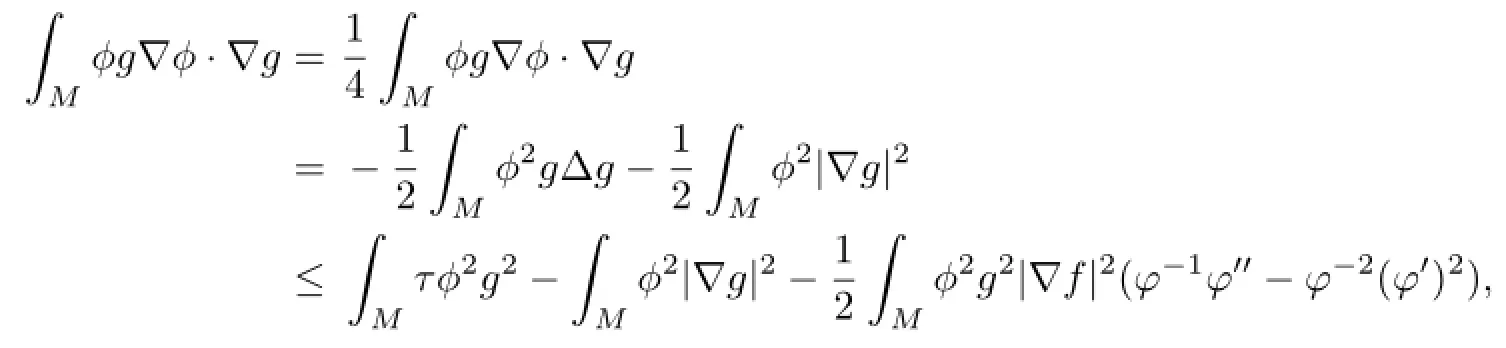
it follows that

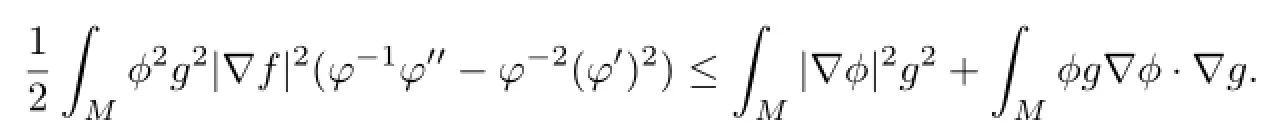
Let

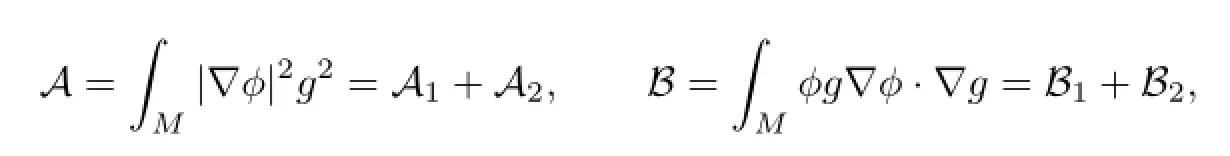
where

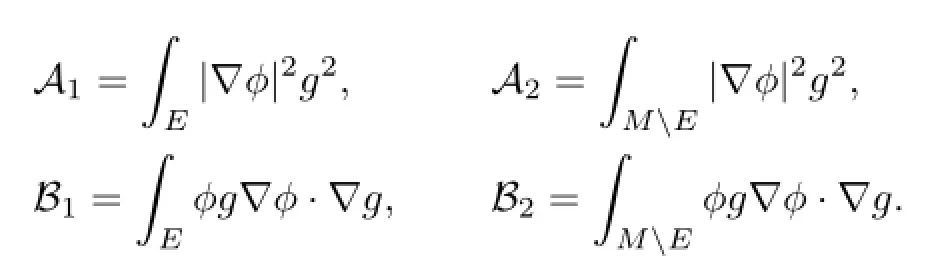
Suppose that the right hand side of(2.3)vanishes as ϕ→1.It implies that

that is,f is a constant function.It contradicts the assumption.Therefore,M has only one nonparabolic end.Now,choose

Thus,

It suffices to prove the following lemma∶

Lemma 2.3AandBvanish if→1.

Proof.We only prove the conclusions for A1and B1.The proofs for A2and B2are similar. Chooseas follows∶

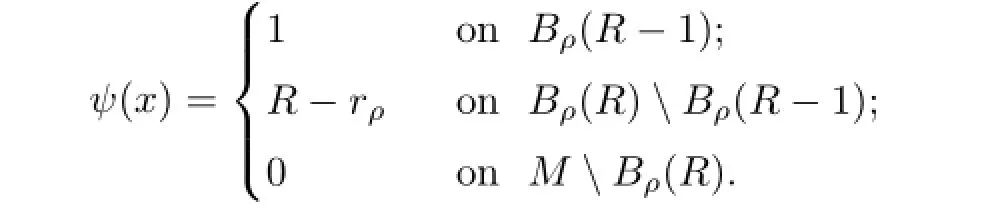
where

Now we prove the following fact∶

for all R＞0(see[8]).Let

Then

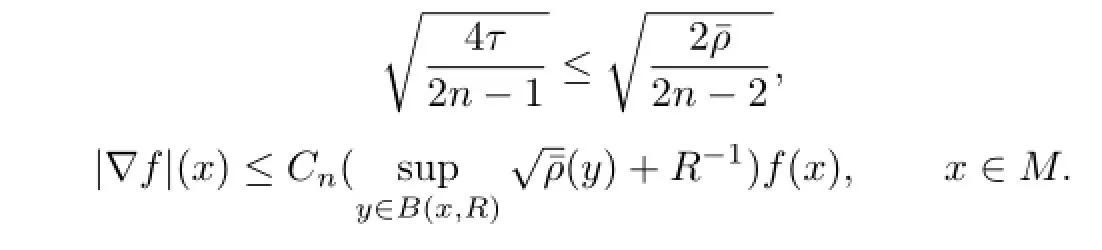
Fix x∈M and consider the function

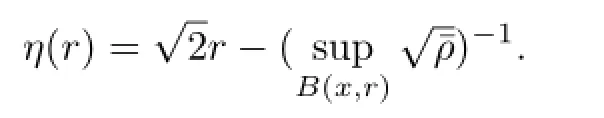
Obviously,η(r)tends to a negative number as r→0 and tends to+∞as r→+∞.Thus, there exists an r0depending on x such that

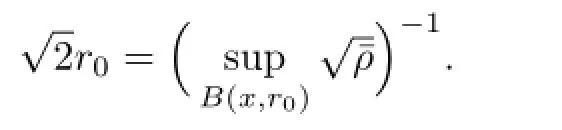
Hence,

For any y∈B(x,r0),let γ be a minimizing geodesic with respect to the background metric ds2jointing x and y.Then

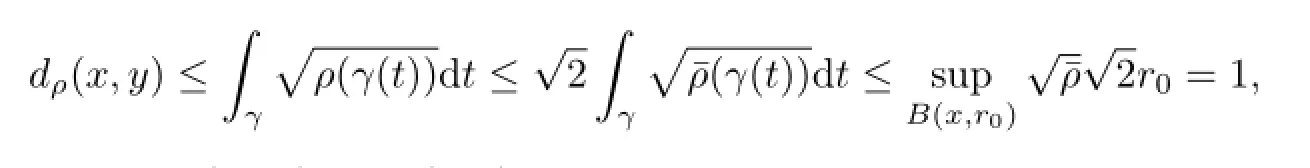
which implies that B(x,r0)⊆Bρ(x,1).Hence,

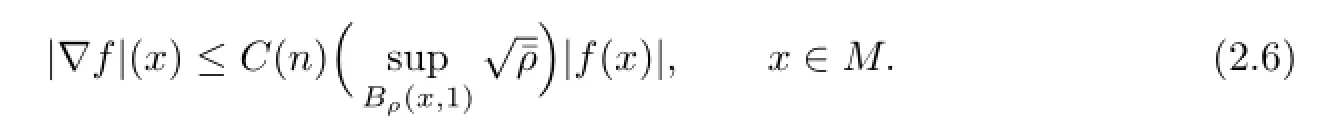
Thus,for any x∈Bρ(R)∩L(σϵ,ϵ),

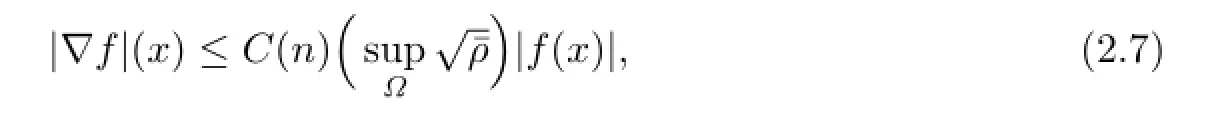
where

Note that the assumption on ρ and τ implies that

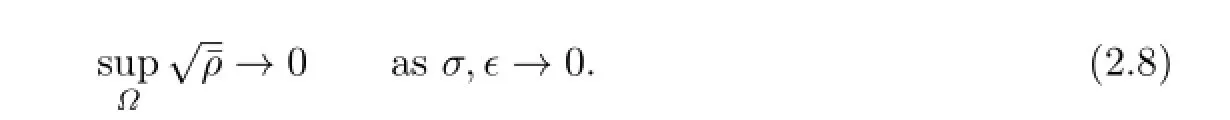
Recall that,under the assumption that the complete manifold M has the property(Pρ), one has the decay estimation for f(see(2.10)in[2])∶

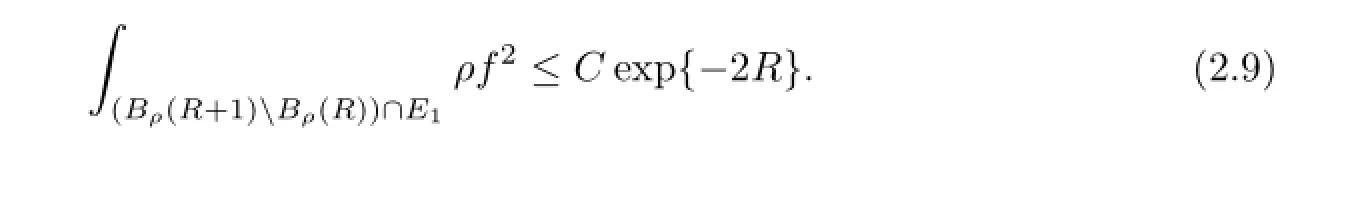
Thus,

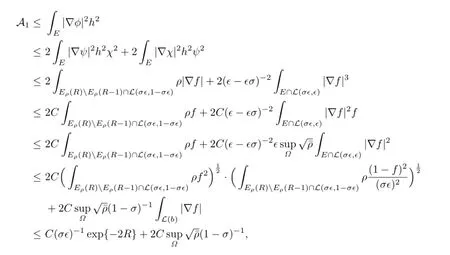
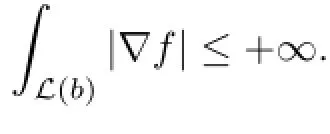
In addition,we have

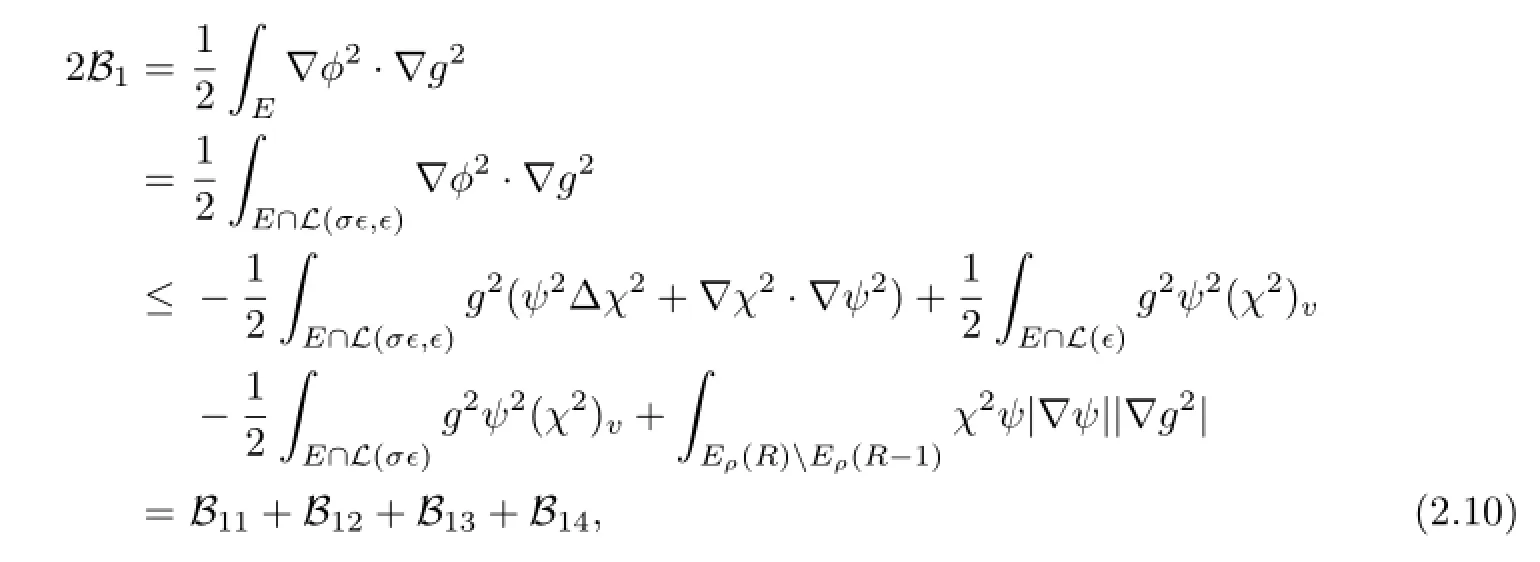
Similarly,there is

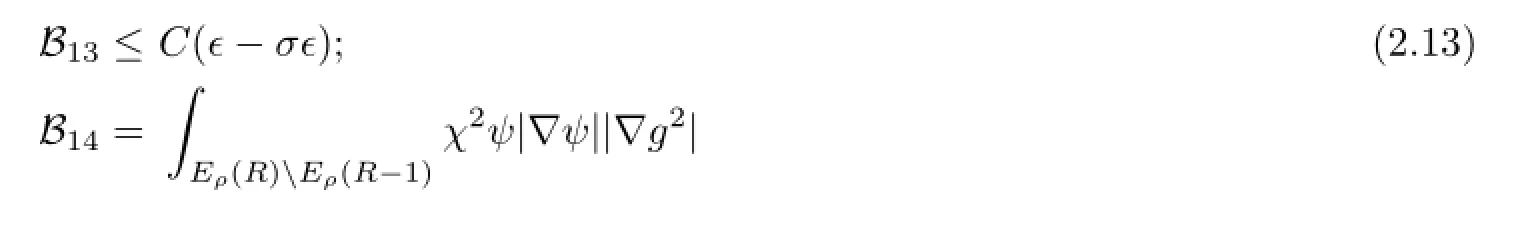
where the last inequality holds because of Corollary 2.3 of[2],

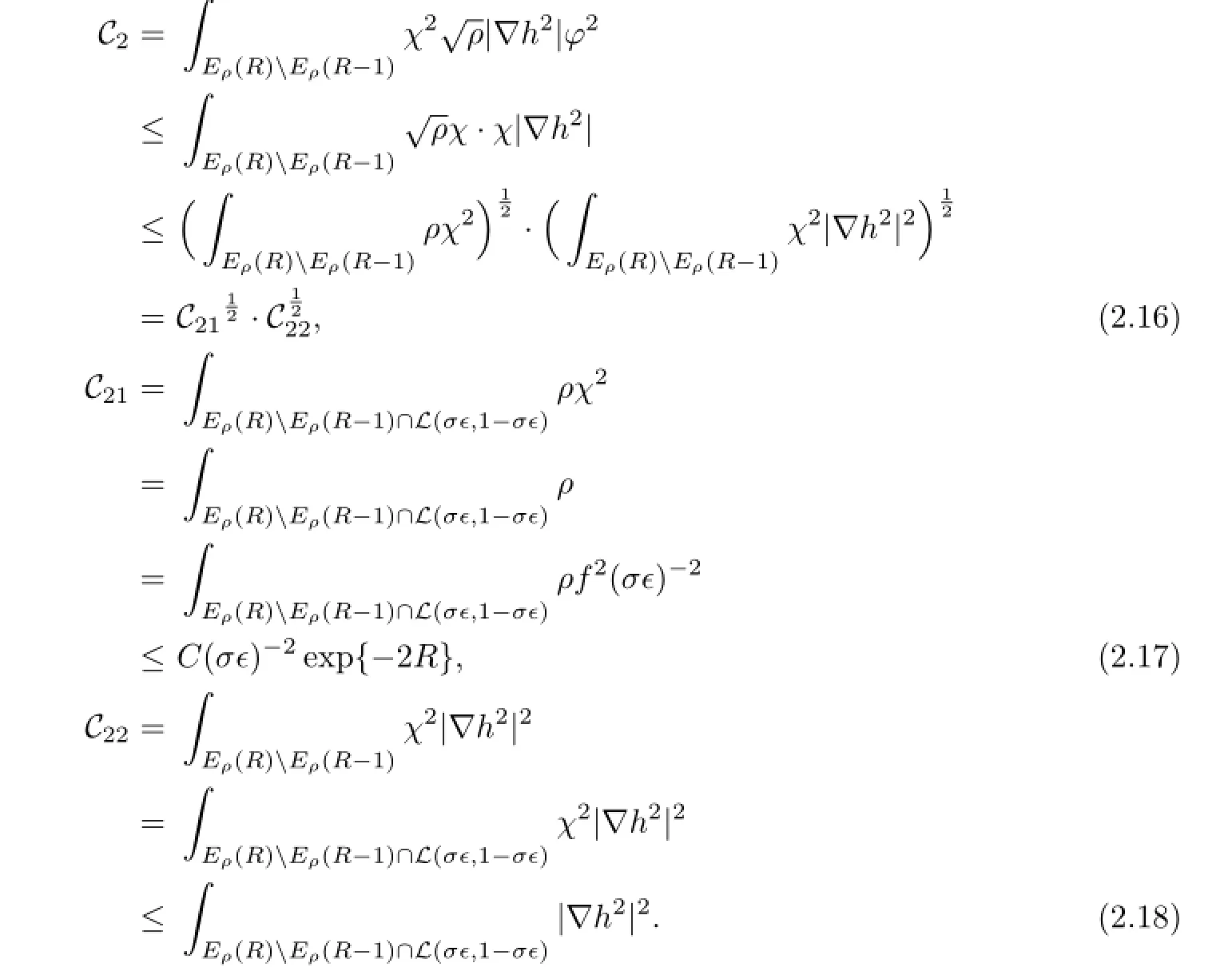
Note that there is the following inequality from Bochner’s formula∶

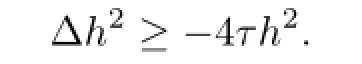
Suppose that

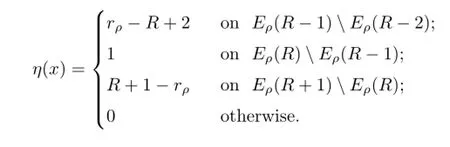
Thus,

So,

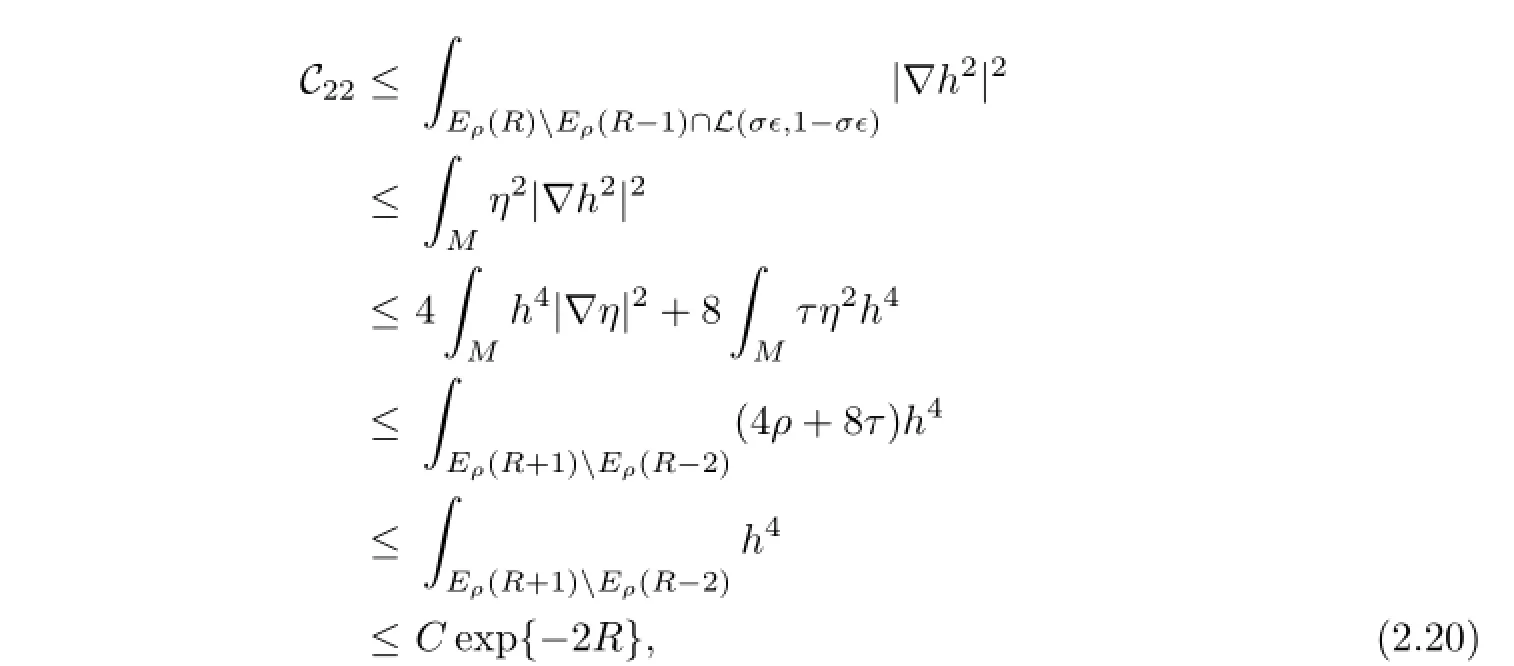
where the last inequality holds because of Corollary 2.3 of[2].Combining(2.10)–(2.20), letting R→∞and δ,ϵ→0,we obtain that A and B vanish.

[1]Li P,Wang J P.Complete manifolds with positive spectrum I.J.Di ff erential Geom.,2001,58: 501–534.

[2]Li P,Wang J P.Complete manifolds with positive spectrum II.J.Di ff erential Geom.,2002,62: 143–162.

[3]Li P,Wang J P.Weighted Poincar´e inequality and rigidity of complete manifolds.Ann.Sci. ´Ecole Norm.Sup.,2006,39:921–982.

[4]Cheng X,Zhou D T.Manifolds with weighted Poincar´e inequality and uniqueness of minimal hypersurfaces.Comm.Anal.Geom.,2009,17(1):135–154.

[5]Munteanu O.Two results on the weighted Poincar´e inequality on complete K¨ahler manifolds. Math.Res.Lett.,2007,14:995–1008.

[6]Li P,Tam L F.Harmonic functions and the structure of complete manifolds.J.Di ff erential Geom.,1992,35:359–383.

[7]Lam K H.Results on a weighted Poincar´e inequality of complete manifolds.Trans.Amer.Math. Soc.,2010,362:5043–5062.

[8]Cheng S Y,Yau S T.Di ff erential equations on Riemannian manifolds and their geometric applications.Comm.Pure Appl.Math.,1975,28:333–354.

tion:53C21,54C42

A

1674-5647(2014)03-0237-08

10.13447/j.1674-5647.2014.03.05

Received date:May 16,2011.

Foundation item:The NSF(11101352)of China,New Century Talent Project of Yangzhou University,Fund of Jiangsu University of Technology(KYY 13005)and Qing Lan Project.

E-mail address:zhupeng2004@126.com(Zhu P).