λ-central BMO Estimates for Higher Order Commutators of Hardy Operators

(1.Department of Mathematics,Mudanjiang Normal University, Mudanjiang,Heilongjiang,157011)

(2.Laboratory for Multiphase Processes,University of Nova Gorica, Nova Gorica,5000,Slovenia)

λ-central BMO Estimates for Higher Order Commutators of Hardy Operators

WU JIANG-LONG1AND LIU QING-GUO2

(1.Department of Mathematics,Mudanjiang Normal University, Mudanjiang,Heilongjiang,157011)

(2.Laboratory for Multiphase Processes,University of Nova Gorica, Nova Gorica,5000,Slovenia)

Communicated by Ji You-qing

In this paper,theλ-central BMO estimates for higher order commutators of Hardy operators on central Morrey spaceLq,λ(Rn)are established.In the meanwhile,the corresponding corollary for central BMO estimates is also obtained.

λ-central BMO space,commutator,Hardy operator,central Morrey space

1 Introduction and Main Result

Let f be a locally integrable function onRn.The n-dimensional Hardy operators are de fi ned by

In 1995,Christ and Grafakos[1]obtained results for the boundedness ofon Lp(Rn)(1＜p＜∞)spaces.They also found the exact operator norms ofon Lp(Rn)(1＜p＜∞) spaces.

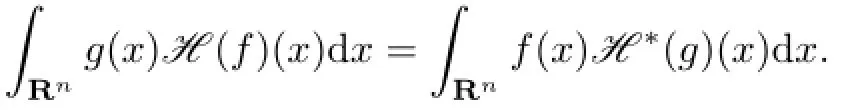
And we have|H(f)(x)|≤CnMf(x),where M is the Hardy-Littlewood maximal operator which is de fi ned by

where the supremum is taken over all balls containing x.

In 2007,Fuet al.[2]gave the central BMO estimates for commutators,Hb(f)and(f), of n-dimensional Hardy operators,where b is a locally integrable function onRn,Hb(f) and(f)are de fi ned as follows∶

In 2000,Alvarezet al.[3]studied the relationship between central BMO spaces and Morrey spaces.Furthermore,they introduced λ-central bounded mean oscillation spaces and central Morrey spaces,respectively.

where

and|B(0,r)|is the measure ofB(0,r).

Remark 1.1If two functions which di ff er by a constant are regarded as a function in the space CBMOq,λ(Rn),then CBMOq,λ(Rn)becomes a Banach space.Apparently,(1.1) is equivalent to the condition(see[3–4])

where

and|B(0,r)|is the measure ofB(0,r).

Remark 1.2It follows from(1.1)and(1.2)that Lq,λ(Rn)is a Banach space continuously included in CBMOq,λ(Rn).

Fu[4]considered λ-central BMO estimates for commutators of n-dimensional Hardy operators,and Fuet al.[5]established λ-central BMO estimates for commutators of singular integral operators with rough kernels.

Inspired by[2,4–8],we establish the λ-central BMO estimates for higher order commutators of n-dimensional Hardy operators on central Morrey spaces.

De fi nition 1.3Letbbe a locally integrable function onRn,andm∈Z+.We de fi ne the higher order commutators ofn-dimensional Hardy operators as follows∶

wherex∈Rn{0}.

Ifb∈CBMOmp2,λ2(Rn),then

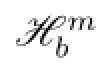
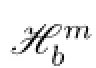
Ifb∈CBMOmp2(Rn),then

Throughout this paper,C denotes a constant that is independent of the main parameters involved but whose value may di ff er from line to line.For any index p∈[1,∞],we denote by p′its conjugate index,namely,

2 Proof of Theorem 1.1

Proof.(i) Let f be a function in Lp1,λ(Rn).For fi xed r＞0,denote B(0,r)by B.Write

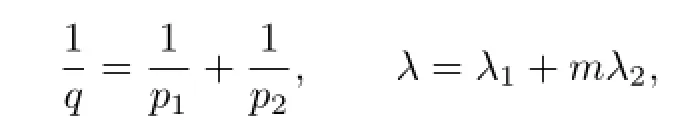
For

We now estimate I2,and divide I2into two parts∶

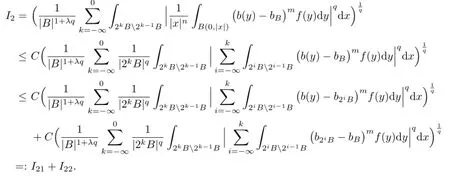
For I21,by Hlder’s inequality,we obtain

where the convergence of these two series are due to the facts that

and

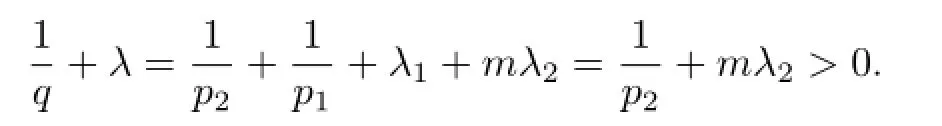
To estimate I22,we should fi rst give the estimate of|b2iB−bB|m(i≤k≤0).For λ2≥0, we have

By H¨older’s inequality and the above estimate,we have

where the convergence of these two series are due to the facts that

and

By combining the estimates of I1,I21and I22,the proof is fi nished.

(ii)We omit the details here.

[1]Chirst M,Grafakos L.Best constants for two non-convolution inequalities.Proc.Amer.Math. Soc.,1995,123:1687–1693.

[2]Fu Z,Liu Z,Lu S,et al.Characterization for commutators of n-dimensional fractional Hardy operators.Sci.China Ser.A,2007,50(10):1418–1426.

[3]Alvarez J,Guzm´an-Partida M,Lakey J.Spaces of bounded λ-central mean oscillation,Morrey spaces,and λ-central Carleson measures.Collect.Math.,2000,51(1):1–47.

[4]Fu Z.λ-central BMO estimates for commutators of n-dimensional Hardy operators.J.Inequal. Pure Appl.Math.,2008,9(4),Article ID 111,5 pp.

[5]Fu Z,Lin Y,Lu S.λ-Central BMO estimates for commutators of singular integral operators with rough kernels.Acta Math.Sinica(Engl.Ser.),2008,3:373–386.

[6]Long S,Wang J.Commutators of Hardy operators.J.Math.Anal.Appl.,2002,274:626–644.

[7]Wu J,Tao S.CBMO estimates for the commutator and multilinear operators of fractional integrals with rough kernel on homogeneous Morrey-Herz spaces(in Chinese).J.Jilin Univ. Sci.,2009,47(3):431–440.

[8]Lu S,Yang D.The central BMO spaces and Littlewood-Paley operators.Approx.Theory Appl. (N.S.),1995,11(3):72–94.

tion:26D15,42B25,42B99

A

1674-5647(2014)03-0201-06

10.13447/j.1674-5647.2014.03.02

Received date:May 29,2012.

Foundation item:The Pre-research Project(SY201224)of Provincial Key Innovation,the Scienti fi c and Technical Research Project(12531720)of the Education Department of Heilongjiang Province,the NSF(A200913) of Heilongjiang Province,and the NSF(11041004,11161042,11071250)of China.

E-mail address:jl-wu@163.com(Wu J L).