Vertex-distinguishing IE-total Colorings of Cycles and Wheels

(College of Mathematics and Information Science,Northwest Normal University, Lanzhou,730070)

Vertex-distinguishing IE-total Colorings of Cycles and Wheels

CHEN XIANG-EN,HE WEN-YU,LI ZE-PENG AND YAO BING

(College of Mathematics and Information Science,Northwest Normal University, Lanzhou,730070)

Communicated by Du Xian-kun

Let G be a simple graph.An IE-total coloring f of G refers to a coloring of the vertices and edges of G so that no two adjacent vertices receive the same color. Let C(u)be the set of colors of vertex u and edges incident to u under f.For an IE-total coloring f of G using k colors,if C(u)C(v)for any two di ff erent vertices u and v of V(G),thenfis called a k-vertex-distinguishing IE-total-coloring of G, or a k-VDIET coloring of G for short.The minimum number of colors required for a VDIET coloring of G is denoted by(G),and is called the VDIET chromatic number of G.We get the VDIET chromatic numbers of cycles and wheels,and propose related conjectures in this paper.

graph,IE-total coloring,vertex-distinguishing IE-total coloring,vertexdistinguishing IE-total chromatic number

1 Introduction and Preliminaries

For an edge coloring(proper or not)of a graph G and a vertex v of G,denote by S(v)the set of colors used to color the edges incident to v.

A proper edge coloring of a graph G is said to be vertex-distinguishing if each pair of vertices is incident to a di ff erent set of colors.In other words,S(u)S(v)whenever uv. A graph G has a vertex-distinguishing proper edge coloring if and only if it has no more than one isolated vertex and no isolated edges.Such a graph is referred to as a vdec-graph. The minimum number of colors required for a vertex-distinguishing proper edge coloringof a vdec-graph G is denoted by(G).The concept of vertex-distinguishing proper edge coloring has been considered in several papers(see[1–7]).

A general edge coloring(not necessarily proper)of a graph G is called vertex-distinguishing if S(u)≠S(v)is required for any two distinct vertices u and v.The point-distinguishing chromatic index of a vdec-graph G,denoted by χ0(G),refers to the minimum number of colors required for a vertex-distinguishing general edge coloring of G.This parameter was introduced by Harary and Plantholt in[8].In spite of the fact that the structure of complete bipartite graph is simple,it seems that the problem of determining χ0(Km,n)is not easy, especially in the case m=n,as documented by papers of Horˇn´ak and Sot´ak[9–10],Zagaglia Salvi[11–12]and Horˇn´ak and Zagaglia Salvi[13].

For a total coloring(proper or not)f of G and a vertex v of G,denote by Cf(v),or simply C(v)if no confusion arises,the set of colors used to color the vertex v as well as the edges incident to v.Let(v)be the complementary set of C(v)in the set of all colors we used.Obviously|C(v)|≤dG(v)+1 and the equality holds if the total coloring is proper.

For a proper total coloring,if C(u)C(v),i.e.,(u)(v)for any two distinct vertices u and v,then the coloring is called vertex-distinguishing(proper)total coloring and the minimum number of colors required for a vertex-distinguishing(proper)total coloring is denoted by χvt(G).This concept has considered in[14–15].In[15],the authors give the following conjecture.

From[15]we know that the above conjecture is valid for complete graphs,complete bipartite graphs,path and cycle,etc.

In this paper we propose a kind of vertex-distinguishing general total coloring.The relationship of this coloring and vertex-distinguishing proper total coloring is similar to the relationship of vertex-distinguishing general edge coloring and vertex-distinguishing proper edge coloring.

When we de fi ne a proper total coloring of a graph G,we need three conditions for a total coloring which are listed as follows∶

Condition(v)∶No two adjacent vertices receive the same color;

Condition(e)∶No two adjacent edges receive the same color;

Condition(i)∶No edge receives the same color as one of its endpoints.

If we only consider the total coloring of the graph G such that the Condition(v)is satis fi ed,then such a coloring is called an IE-total coloring of the graph G.

If f is an IE-total coloring of the graph G using k colors and for all u,v∈V(G),uv, we have C(u)C(v),then f is called a k-vertex-distinguishing IE-total coloring,or a k-VDIET coloring.The minimum number k for which G has a k-VDIET coloring is called the vertex-distinguishing IE-total chromatic number(or VDIET chromatic number)of the graph G and is denoted by

The following proposition is obviously true.

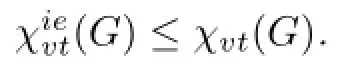
Proof.For a graph G,let nibe the number of the vertices of degree i,δ≤i≤Δ.Suppose that

In Section 2 we consider the VDIET colorings for cycles and paths.The discussions of the VDIET colorings for wheels and fans are long,so we put them into the Section 3.In Section 4 we give two conjectures.

2 Vertex Distinguishing IE-total Chromatic Numbers of Cycle and Path

Theorem 2.1LetCnbe a cycle of ordern(n≥3).Then

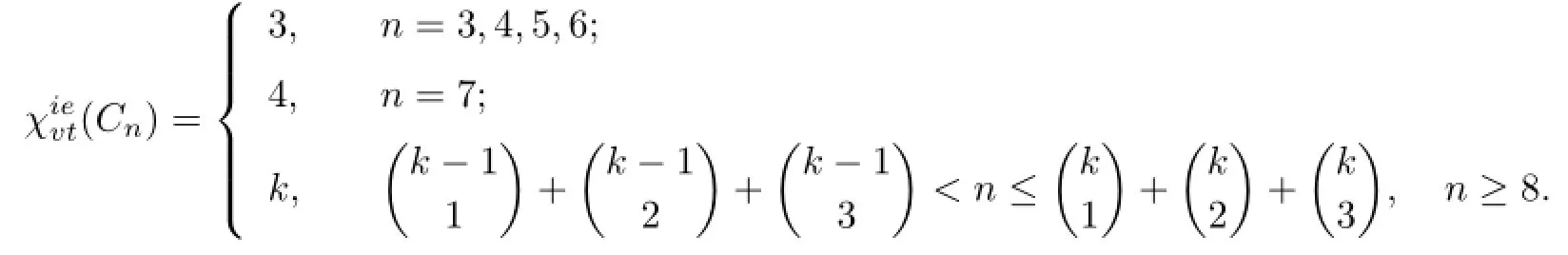
Proof.When n=3,4,5,6,the results are obviously true.Let Cn=u1u2u3···unu1.In this proof when we want to give a k-VDIET coloring fnof Cnwith all colors 1,2,···,k,we need only to give(fn(ui−1ui),fn(ui),fn(uiui+1))or fn(ui−1ui)fn(ui)fn(uiui+1)for each i=1,2,···,n,i.e.,

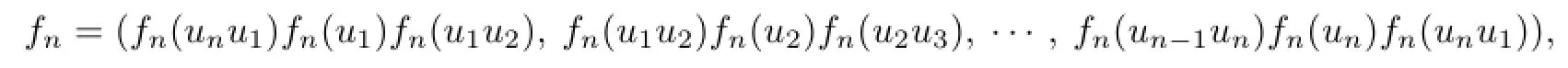
such that

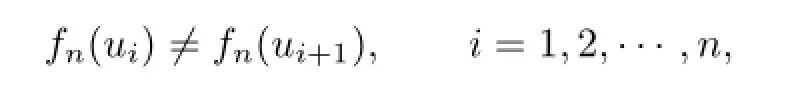
and

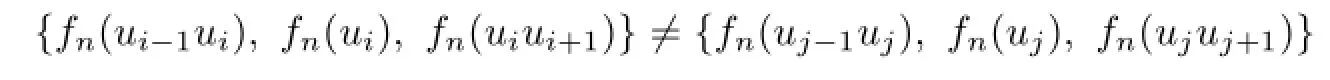
If n=7,then

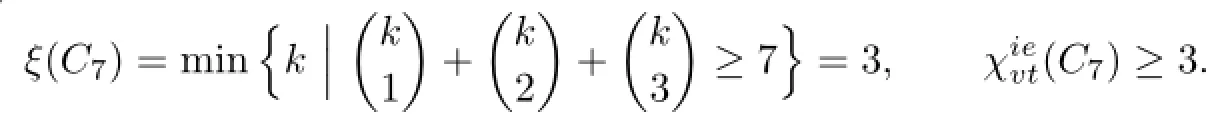
Assume that C7has a 3-VDIET coloring g.Then there are three vertices such that their color sets are{1},{2}and{3},respectively.But no two such vertices are adjacent.So without loss of generality we assume that C(u1)={1},C(u3)={2},C(u5)={3}.As no two adjacent vertices receive the same color,the colors that u2and u4are assigned under g are 3 and 1,respectively.Thereby u2and u4have the same color set,which is a contradiction.So there does not exist a VDIET coloring of C7using 3 colors.

Obviously,

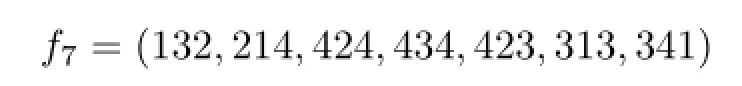
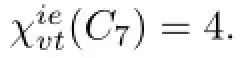
If

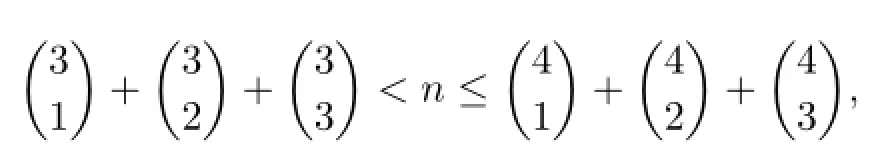
i.e.,8≤n≤14,then

Let

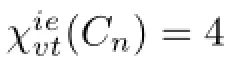
If

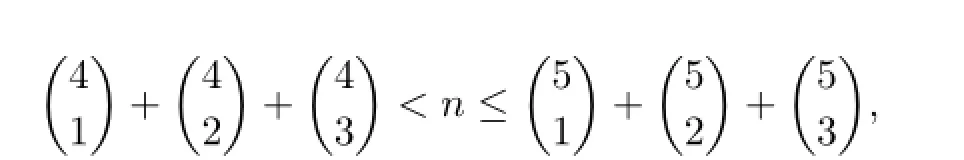
i.e.,15≤n≤25,then

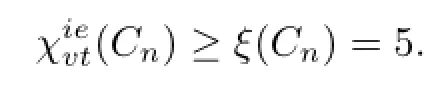
Let

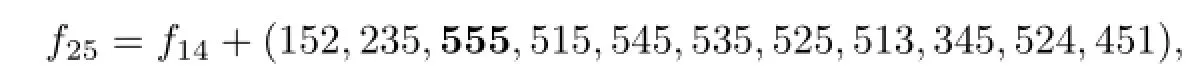
where“+”denotes the concatenation of sequence.Obviously,when 15≤n≤25,fnis a 5-VDIET coloring of Cn,so the result holds.

We now want to apply the same technique to give fnfor

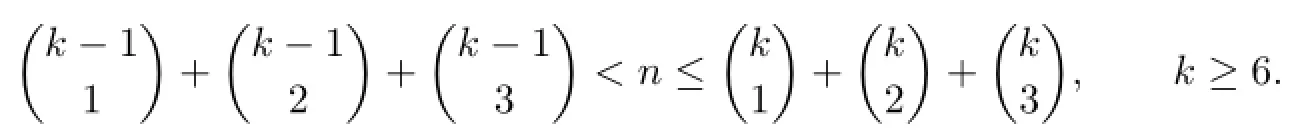
To do so,we de fi ne Ckat fi rst.Let

If l≡0(mod 4),let

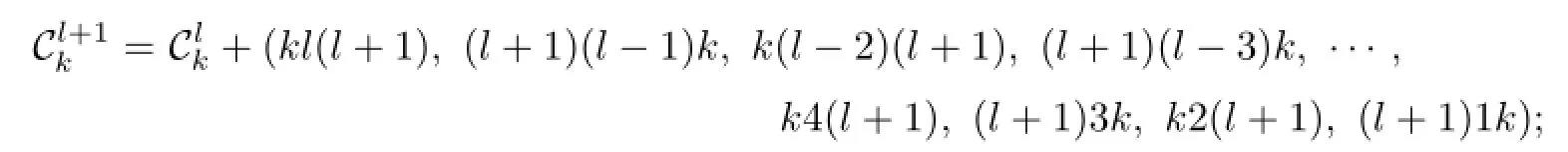
If l≡1(mod 4),let

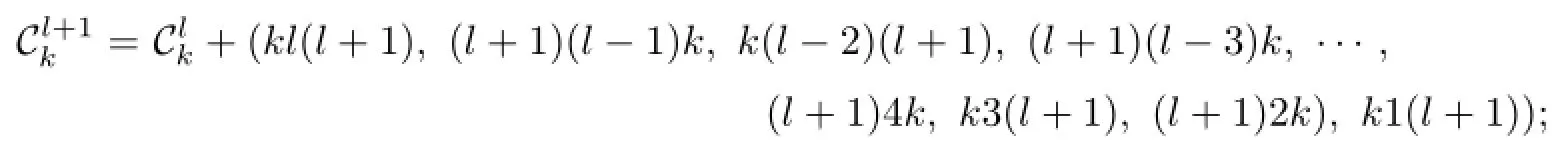
If l≡2(mod 4),let

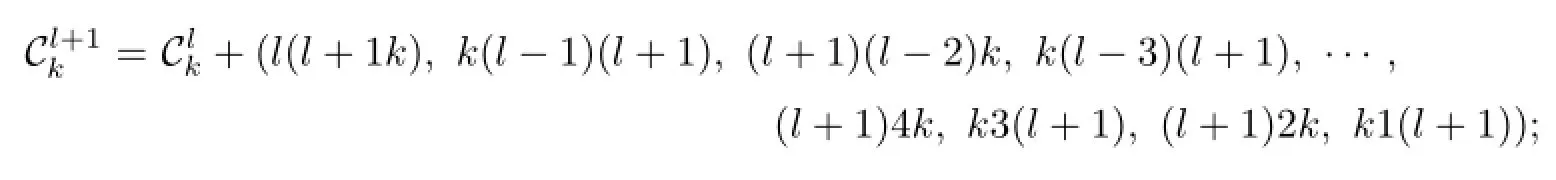
If l≡3(mod 4),let

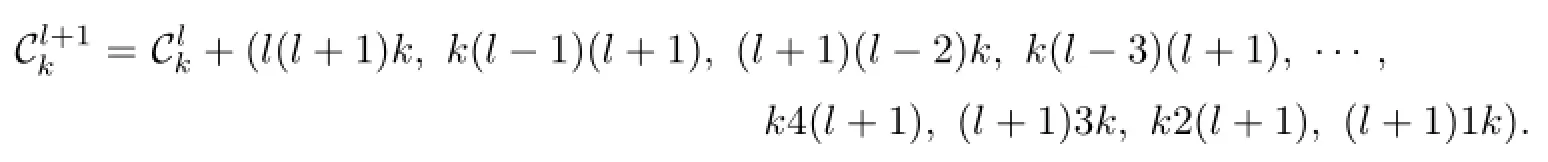
For l=6,7,···,k−2,we do the above work step by step.Finally we obtain.The last term ofis(k−1)1k or k1(k−1).We change the last term(k−1)1k to(k−1)k1 and k1(k−1)to k(k−1)1.And the resulting sequence is denoted by Ck.

Now we determine fnwhen

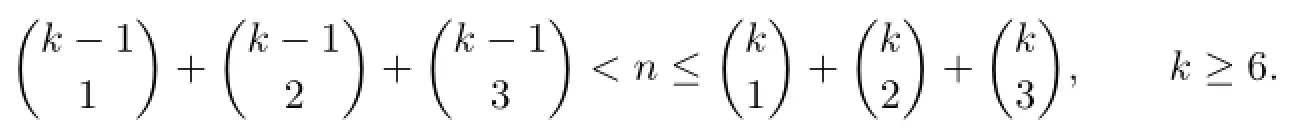
Suppose

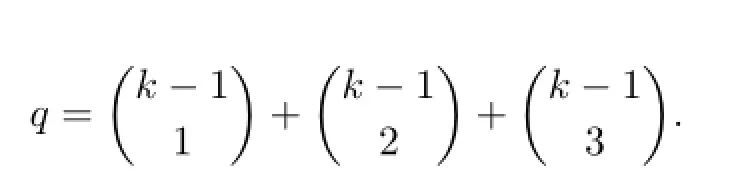
Let

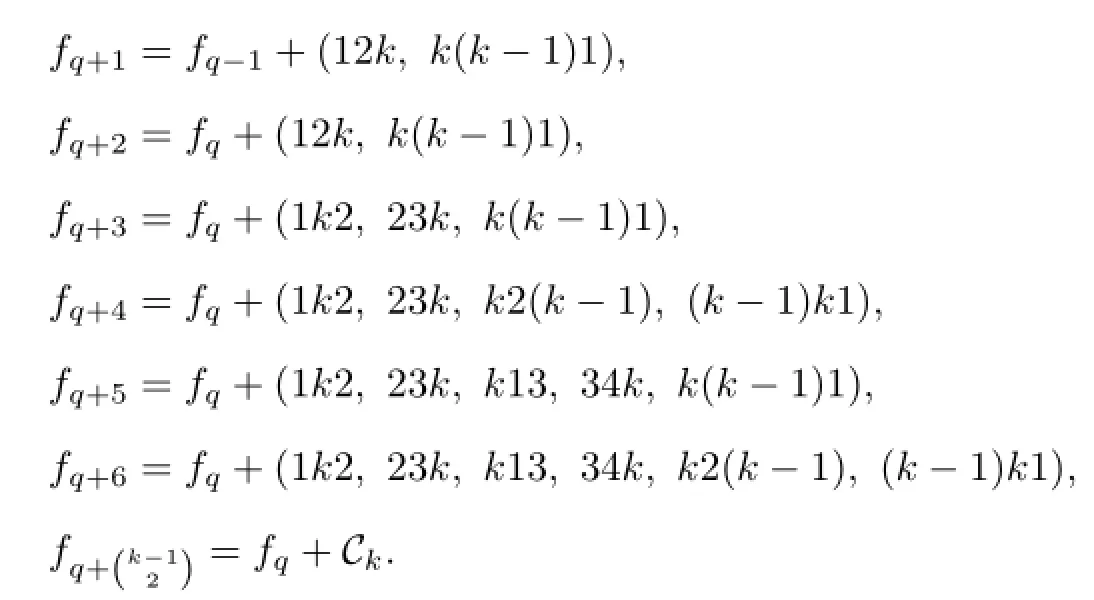
Theorem 2.2For a pathPnof ordern(≥8),if

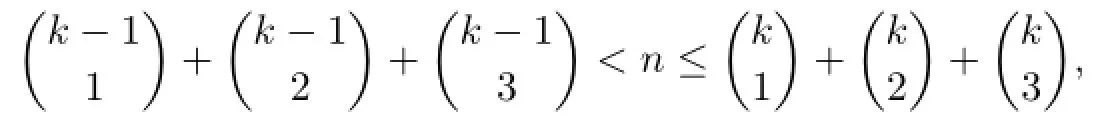
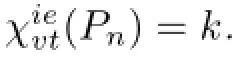
Proof.If

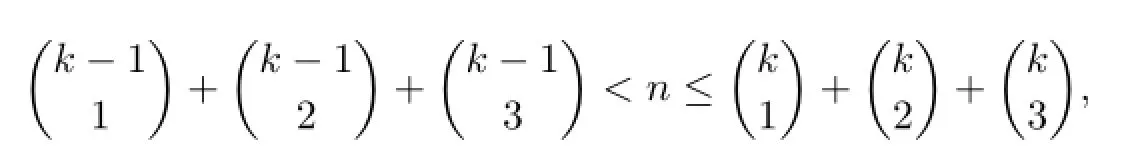
Actually,based on the k-VDIET coloring fnof Cn=u1u2u3···unu1de fi ned in the above theorem,if we delete the edge which connects two vertices with color sets{4,2}and{4,3}, i.e.,the corresponding terms are 424 and 434,then we can obtain Pnand its k-VDIET coloring when

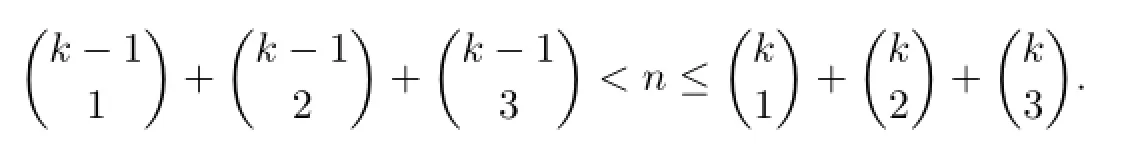
3 Vertex Distinguishing IE-total Chromatic Numbers of Wheel and Fan

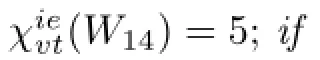
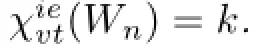
Proof.Let

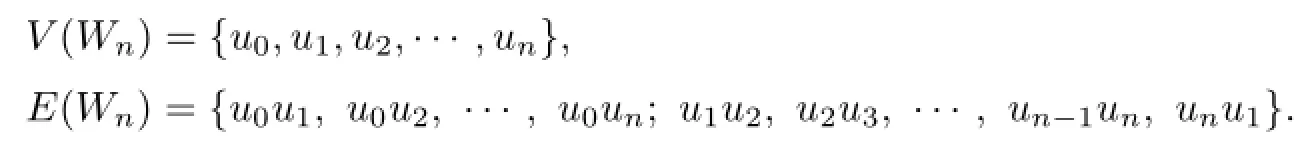
In this proof,when we want to give a k-VDIET coloring fnof Wn,we always appoint that the colors which we use are 1,2,···,k,the color of u0is k,and then it suffices to give (fn(ui−1ui),fn(u0ui),fn(ui),fn(uiui+1))or fn(ui−1ui)fn(u0ui)fn(ui)fn(uiui+1)for each i=1,2,···,n,equivalently to give

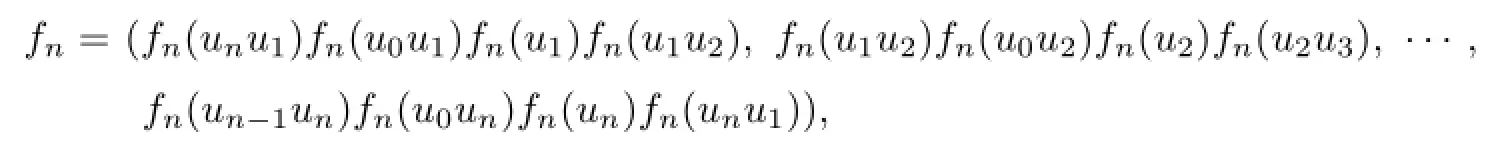
such that fn(ui)fn(ui+1),i=1,2,···,n,and

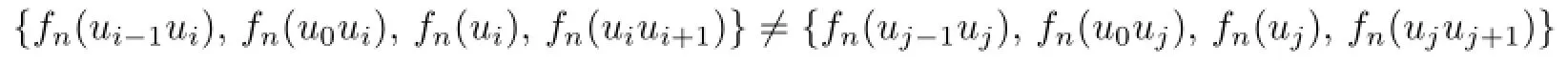
If n=4,then

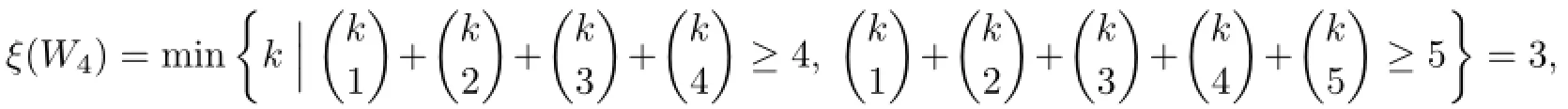
Case 1.|C(u0)|=1.Then C(u0)={3},and each C(ui),i=1,2,3,4,is one of{1,2,3}, {2,3},{1,3}.Three subsets can not distinguish 4 vertices.It is a contradiction.

Case 2.|C(u0)|=2.We may suppose C(u0)={3,2}.Then each C(ui),i=1,2,3,4,is one of{1,2,3},{1,2},{1,3},{2}.Let C(u1)={2}.Then the colors of u2and u4are only 1.Thus{C(u2),C(u4)}={{1,2,3},{1,2}}.So C(u3)={1,3}and the color of u3is 2 for ensuring the vertex coloring proper.This is a contradiction.

Case 3.|C(u0)|=3.Of course C(u0)={1,2,3}.Then each C(ui),i=1,2,3,4,is one of{1,2},{2,3},{1,3},{1},{2}.

(a)If{C(u1),C(u2),C(u3),C(u4)}={{1,2},{1,3},{1},{2}},then two vertices which has color sets{1}and{2}are not adjacent.But these two vertices must have the same color.This is a contradiction.

(b)If{C(u1),C(u2),C(u3),C(u4)}={{1,2},{1,3},{2,3},{1}},without loss of generality,we assume C(u1)={1}.Then 1∈C(u2)∩C(u4).Thus C(u3)={2,3},whichyields g(u3)=2.But g(u1)=1,so the color that u2is assigned under g is one of g(u1), g(u3)and g(u0).This is a contradiction.

(c)If{C(u1),C(u2),C(u3),C(u4)}={{1,2},{2,3},{1},{2}},then similar to(a)we can get a contradiction.

(d)If{C(u1),C(u2),C(u3),C(u4)}={{1,2},{1,3},{2,3},{2}},then similar to(b) we can get a contradiction.

(e)If{C(u1),C(u2),C(u3),C(u4)}={{1,3},{2,3},{1},{2}},then similar to(a)we can get a contradiction.

Thus there does not exist a VDIET coloring of W4using 3 colors,so≥4.We can prove=4 by giving a 4-VDIET coloring f4of W4(note that f4(u0)=4)as follows∶f4=(1132,2214,4323,3411).

As the(proper)vertex chromatic number of W5is χ(W5)=4,χievt(W5)≥4.We can show that=4 by giving a 4-VDIET coloring f5of W5as follows∶

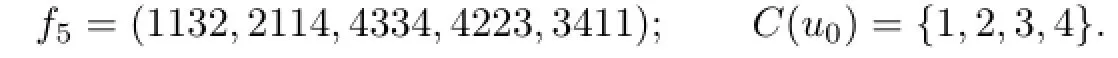
Note that

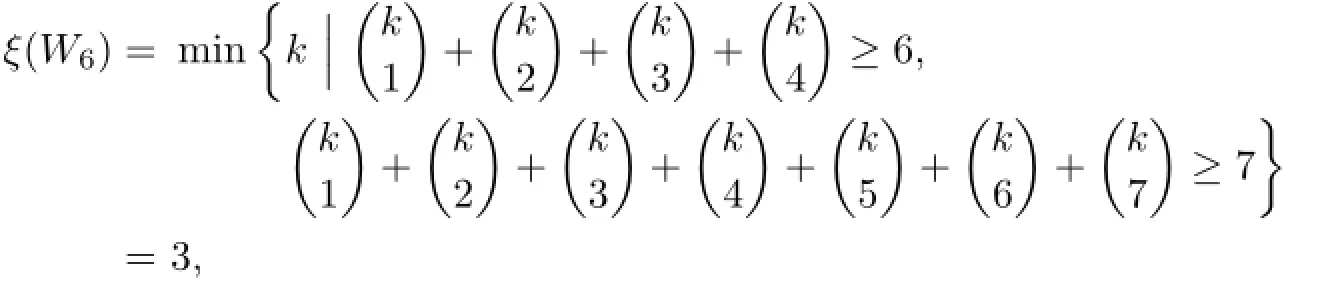
Case 1.|C(u0)|=1.Then C(u0)={3},and each C(ui),i=1,2,···,6,is one of {1,2,3},{2,3},{1,3}.This is a contradiction.

Case 2.|C(u0)|=2.We may suppose C(u0)={3,1}.Then each C(ui),i=1,2,···,6, is one of{1,2,3},{1,2},{2,3},{1}.This is a contradiction.

Case 3.|C(u0)|=3.Then C(u0)={1,2,3},and each C(ui),i=1,2,···,6,is one of{1,2},{2,3},{1,3},{1},{2}.Five subsets do not distinguish six vertices.This is a contradiction.

f13=(1132,2112,2222,2114,4224,4114,4334,4223,3333,3113,3223,3431,1111). It is easy to see that fnis a 4-VDIET coloring of Wnand(Wn)=4 when 7≤n≤13.

Case 1.|C(u0)|=1.Then C(u0)={4},and each C(ui),i=1,2,···,14,is one of {1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}.This is a contradiction.

Case 2.|C(u0)|=2.We may suppose C(u0)={1,4}.Then each C(ui),i=1,2,···,14, is one of{1},{1,2},{1,3},{2,4},{3,4},{1,3,4},{1,2,4},{1,2,3},{2,3,4},{1,2,3,4}. This is a contradiction.

Case 3.|C(u0)|=3.We may suppose C(u0)={1,2,4}.Then each C(ui),i= 1,2,···,14,is one of{1},{2},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,3,4}, {2,3,4},{1,2,3,4}.This is a contradiction.

Case 4.|C(u0)|=4,that is,C(u0)={1,2,3,4}.Then each C(ui),i=1,2,···,14,is one of{1},{2},{3},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4},{1,3,4}, {2,3,4}.This is a contradiction.

f14=(1132,2112,2222,2114,4444,4224,4114,4334,4223,3333,3113,3223,3431,1111).

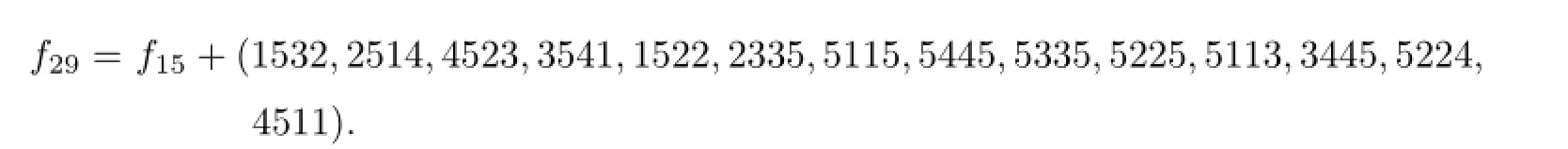
(I)We prove that what wheel has(k−1)-VDIET coloring with colors 1,2,···,k−1 for k≥6.

Suppose that Wnhas a(k−1)-VDIET coloring g.Let|C(u0)|=i.Denote by mithe number of subsets of{1,2,···,k−1}which can be acted as the color set of some uj(1≤j≤n).Then

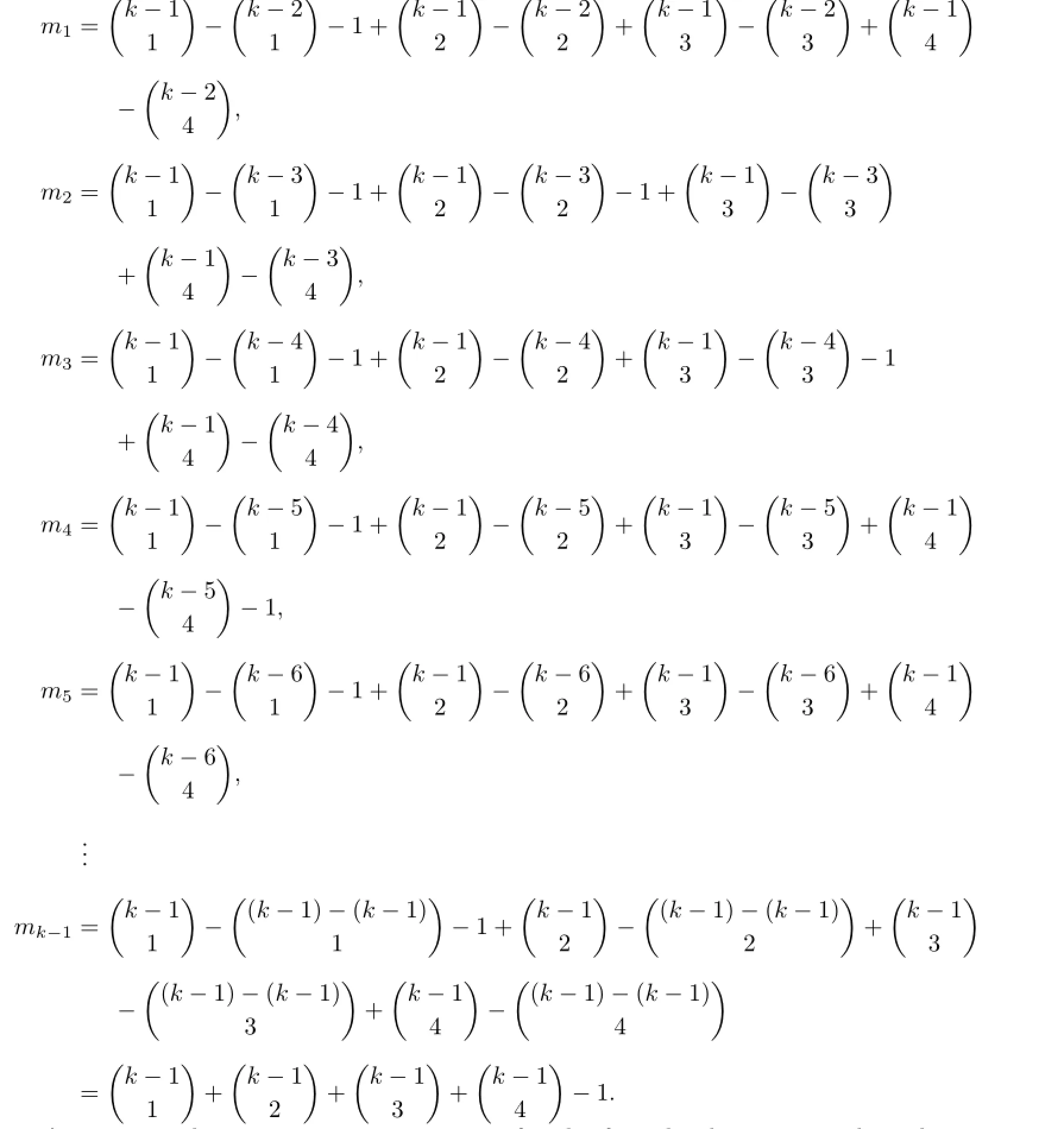
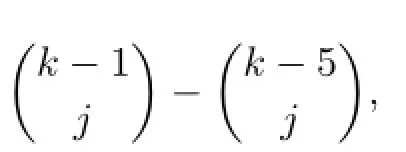
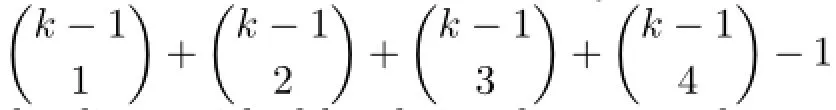
This yields that if

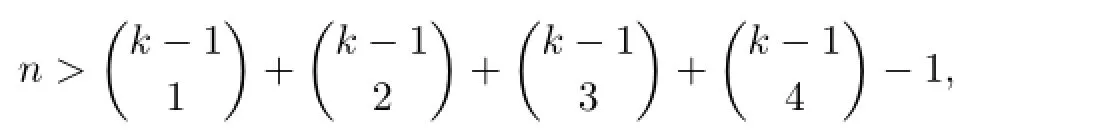
(II)Next we prove that k colors can color Wn,so that the coloring is IE-total coloring and is vertex distinguishing when

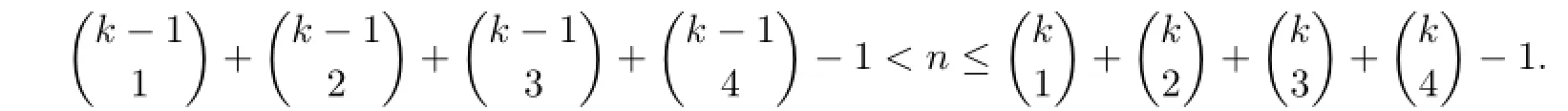
Assume that we have constructed all fiwith

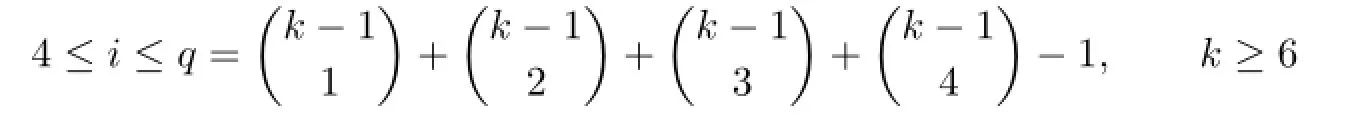
such that

(1)The fi rst term of fiis 1132;

(2)When

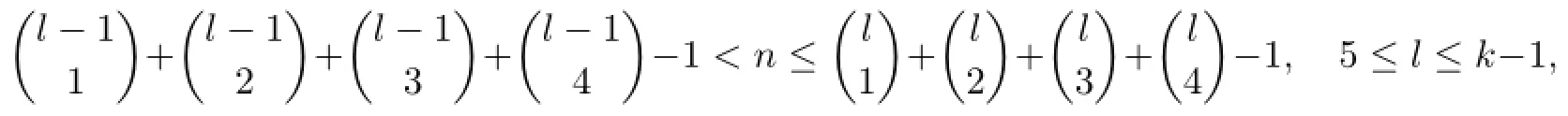
and fn(u0)=l,the fi rst term abcd and the last term a1b1c1d1of fnsatisfy that d1=a=1, c1̸=c and if there are at most 3 di ff erent numbers in{a1,b1,c1,d1}then c1=d1=1;

(3)fqhas used up all 4-combinations,3-combinations,2-combinations and 1-combination of{1,2,···,k−1}except for 1-combination{k−1}.Under fq,C(u0)={1,2,···,k−1}.

Let

and let Cibe the sequence de fi ned in the proof of Theorem 2.1 for i≥7.We change each term abc of Cs,4≤s≤k−1,into akbc,and the resulted sequence is denoted byLetObviously,Dkhasterms.

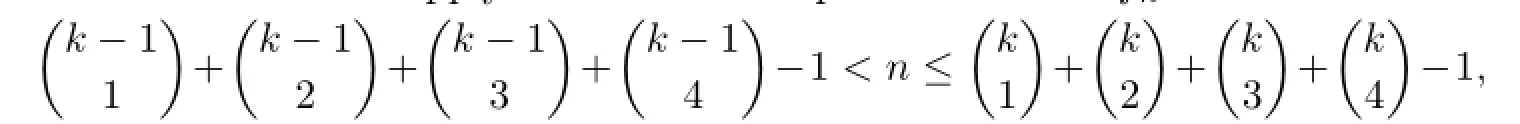
(A)Let fq+1be the sequence formed by inserting the term(k−1)(k−1)(k−1)(k−1) into the place between(k−1)33(k−1)and(k−1)22(k−1)from fq.

(B)Let

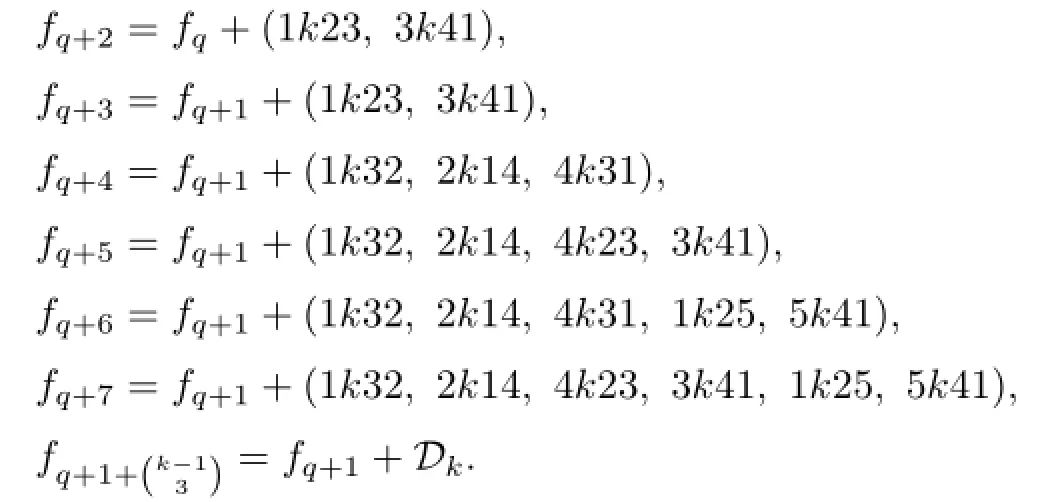
Let

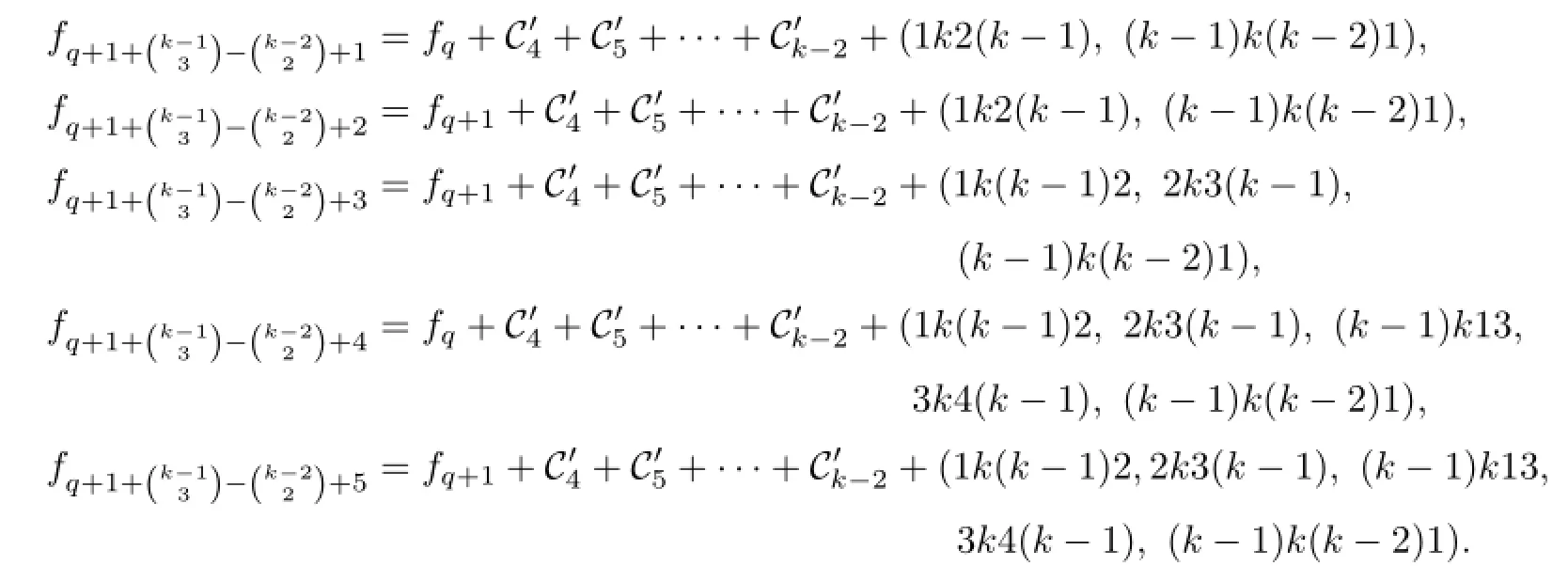
If the(r−1)-th term of Dkis akb(k−1),then we can obtain fq+r+1by adding the fi rst r−1 terms of Dkto fq+1and then adding(k−1)k(k−2)1.

If the(r−1)-th term of Dkis(k−1)kab(but not(k−1)k1s,s≤k−2),then we can obtain fq+r+1by adding the fi rst r−1 terms of Dkto fq+1and then adding bk(k−1)1.

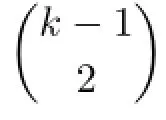
Let

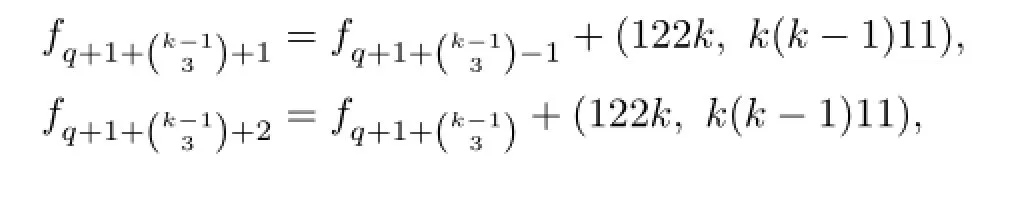
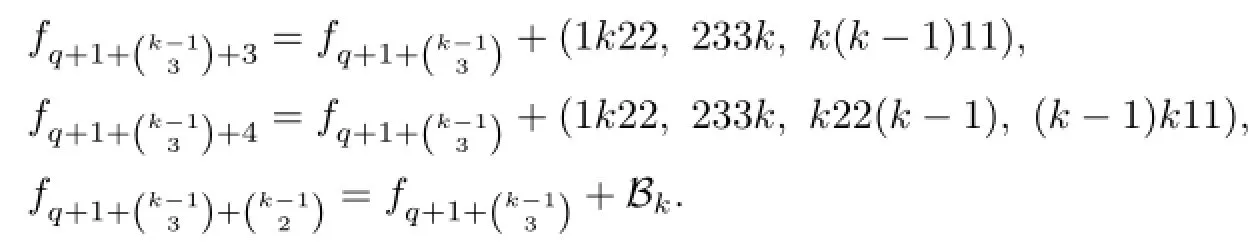
If the(r−1)-th term of Bkis abbk,then we can obtainby adding the fi rst r−1 terms of Bktoand then adding the term k(k−1)11.

If the(r−1)-th term of Bkis of the form kaab(≠k11s,i.e.,a≠1),then we can obtainby adding the fi rst r−1 terms of Bktoand then adding the term bk11.

Theorem 3.2LetFnbe a fan of ordern+1.If3≤ n≤ 4,then(Fn)=3;if5≤n≤13,then

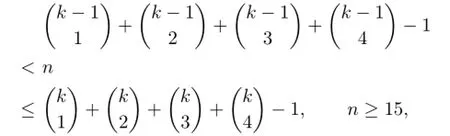
thenχievt(Fn)=k.

Proof.Let

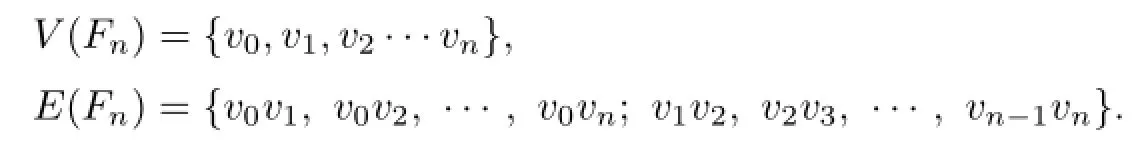
In this proof when we want to give a k-VDIET coloring gnof Fnwith the set of all colors {1,2,···,k},we always appoint that the color of v0is k and then it suffices to give the desired sequence

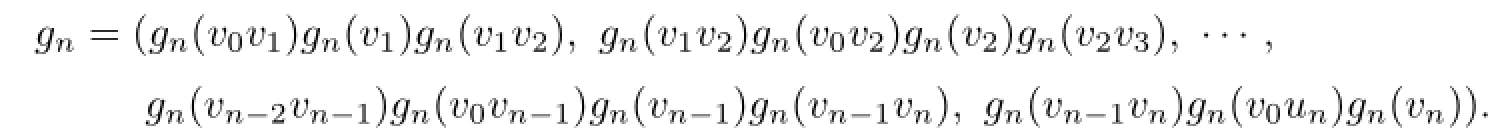
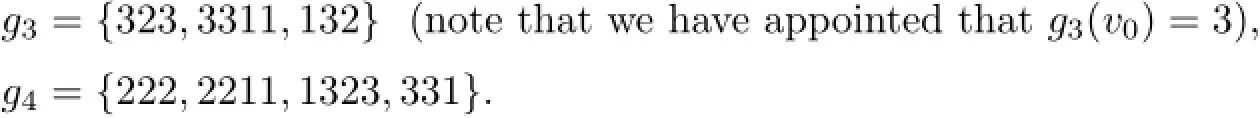
Assume that F5has a 3-VDIET coloring h and h(v0)=3.

If|C(v0)|=1,then 3∈C(vi),i=0,1,···,5.But the number of the subsets of{1,2,3} which contain 3 is 4.This is a contradiction.

If|C(v0)|≥2,then{3}is not the color set of any vertex.Since the vertex coloring is proper,we may suppose h(v1)=h(v3)=h(v5)=1 and h(v2)=h(v4)=2.As{C(v0), C(v1),···,C(v5)}={{1},{2},{1,2},{1,3},{2,3},{1,2,3}},and C(v3)≠{1},without loss of generality we assume that C(v1)={1}and C(v4)={2}.This yields that 2∈C(vi), i=0,2,3,4,5.This is a contradiction for we just have 4 subsets of{1,2,3}which contain 2.

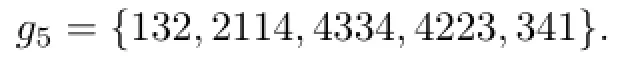
Similarly to proving that W6has no 3-VDIET coloring in the proof of Theorem 3.1 we can show that F6has no 3-VDIET coloring.And

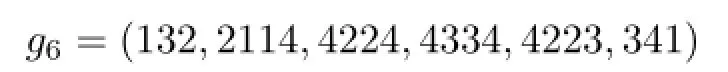
is a 4-VDIET coloring of F6.So=4.

Similarly to the proof that W14has no 4-VDIET coloring in the proof of Theorem 3.1, we can show that F14have no 4-VDIET coloring.And

g14=(132,2112,2222,2114,4444,4224,4114,4334,4223,3333,3113,3223,3431,111). So

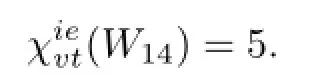
If we delete the fi rst number of the fi rst term of fnand also delete the last number of the last term of fn,then the resulting sequence gnis a 4 or 5-VDIET coloring of Fnwhen 7≤n≤13 or 15≤n≤29.Thus=4 if 7≤n≤13,and=5 if 15≤n≤29. Su

ppose that

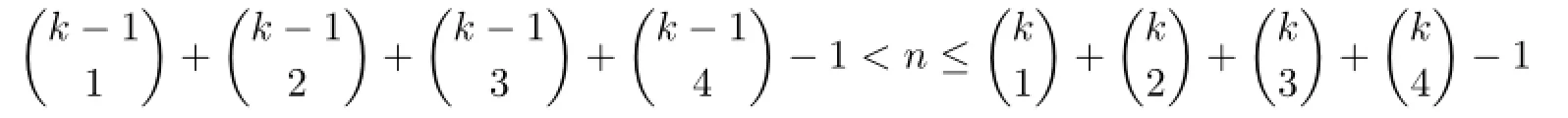
and n≥30.

(I)We can show that Fnhas no(k−1)-VDIET coloring.The process is the same as(I) in the proof of Theorem 3.1.So≥k.

(II)If we delete the fi rst number of the fi rst term of fnand also delete the last number of the last term of fn,then the resulting sequence gnis a k-VDIET coloring of Fn.

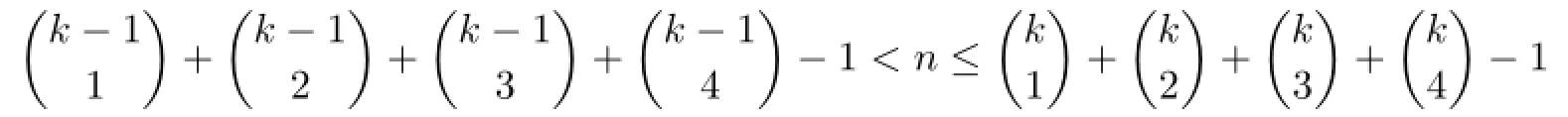
and n≥30.

The proof is completed.

Theorem 3.3LetKnbe the complete graph of ordern(n≥3),then(Kn)=n.

Proof.Any two vertices in Knmust receive di ff erent colors under arbitrary VDIET coloring.Therefore(Kn)≥n.Of course,we are able to show that(Kn)=n by giving a VDIET coloring of Knusing n colors 1,2,···,n as follows.Assign colors 1,2,···,n to vertices v1,v2,···,vnof Knrespectively,and then let all edges receive the same color 1. The proof is completed.

4 Conjectures

From the results obtained in this paper,we know that for any graph G discussed in this paper but Kn(n≥5),we have χievt(G)=ξ(G)or ξ(G)+1.So we propose the following conjectures.

Conjecture 4.1For a simple graphG,if(proper vertex coloring)chromatic numberχ(G)≤4,we have=ξ(G)orξ(G)+1.

Conjecture 4.2For a simple graphG,we have≤max{ξ(G)+1,χ(G)}.

[1]Balister P N,Bollob´as B,Schelp R H.Vertex distinguishing colorings of graphs with Δ(G)=2. Discrete Math.,2002,252:17–29.

[2]Balister P N,Riordan O M,Schelp R H.Vertex distinguishing edge colorings of graphs.J. Graph Theory,2003,42:95–109.

[3]Bazgan C,Harkat-Benhamdine A,Li H,Wo´zniak M.On the vertex-distinguishing proper edge-colorings of graphs.J.Combin.Theory Ser.B,1999,75:288–301.

[4]Burris A C,Schelp R H.Vertex-distinguishing proper edge-colorings.J.Graph Theory,1997,26(2):73–82.

[5]ˇCer´ny J,Horˇn´ak M.Observability of a graph.Math.Slovaca,1996,46:21–31.

[6]Horˇn´ak M,Sot´ak R.Observability of complete multipartite graphs with equipotent parts.Ars Combin.,1995,41:289–301.

[7]Horˇn´ak M,Sot´ak R.Asymptotic behaviour of the observability of Qn.Discrete Math.,1997,176:139–148.

[8]Harary F,Plantholt M.The Point-distinguishing Chromatic Index.In:Harary F,Maybee J S.Graphs and Application.New York:Wiley Interscience,1985:147–162.

[9]Horˇn´ak M,Sot´ak R.The fi fth jump of the point-distinguishing chromatic index of Kn,n.Ars Combin.,1996,42:233–242.

[10]Horˇn´ak M,Sot´ak R.Localization jumps of the point-distinguishing chromatic index of Kn,n. Discuss.Math.Graph Theory,1997,17:243–251.

[11]Zagaglia Salvi N.On the point-distinguishing chromatic index of Kn,n.Ars Combin.,1988,25B:93–104.

[12]Zagaglia Salvi N.On the value of the point-distinguishing chromatic index of Kn,n.Ars Combin.,1990,29B:235–244.

[13]Horˇn´ak M,Zagaglia Salvi N.On the point-distinguishing chromatic index of complete bipartite graphs.Ars Combin.,2006,80:75–85.

[14]Chen X E.Asymptotic behaviour of the vertex-distinguishing total chromatic numbers of n-cube(in Chinese).J.Northwest Norm.Univ.(Natur.Sci.),2005,41(5):1–3.

[15]Zhang Z F,Qiu P X,Xu B G,et al.Vertex-distinguishing total colorings of graphs.Ars Combin.,2008,87:33–45.

tion:05C15

A

1674-5647(2014)03-0222-15

10.13447/j.1674-5647.2014.03.04

Received date:Oct.18,2011.

Foundation item:The NSF(61163037,61163054)of China and the Scienti fi c Research Project(nwnu-kjcxgc-03-61)of Northwest Normal University.

E-mail address:chenxe@nwnu.edu.cn(Chen X E).