Bounded 3-manifolds with Distance n Heegaard Splittings

ZOU YAN-QING AND LIU XI-MIN

(School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024)

Bounded 3-manifolds with Distance n Heegaard Splittings

ZOU YAN-QING AND LIU XI-MIN*

(School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024)

Communicated by Lei Feng-chun

We prove that for any integern≥2andg≥ 2,there are bounded 3-manifolds admitting distancen,genusgHeegaard splittings with any given boundaries.

attaching compression body,Heegaard distance,subsurface projection

1 Introduction

Let S be a compact surface with χ(S)≤−2 but not a 4-punctured sphere.Harvey[1]de fi ned the curve complex C(S)as follows∶The vertices of C(S)are the isotopy classes of essential simple closed curves on S,and k+1 distinct vertices x0,x1,···,xkdetermine a k-simplex of C(S)if and only if they are represented by pairwise disjoint simple closed curves.For two vertices x and y of C(S),the distance of x and y,denoted by dC(S)(x,y),is de fi ned to be the minimal number of 1-simplexes in a simplicial path joining x to y.In other words, dC(S)(x,y)is the smallest integer n≥0 such that there is a sequence of vertices x0=x, ···,xn=y such that xi−1and xiare represented by two disjoint essential simple closed curves on S for each 1≤i≤n.For two sets of vertices in C(S),say X and Y,dC(S)(X,Y) is de fi ned to be min{dC(S)(x,y)|x∈X,y∈Y}.Now let S be a torus or a once-punctured torus.In this case,Masur and Minsky[2]de fi ned C(S)as follows∶The vertices of C(S)are the isotopy classes of essential simple closed curves on S,and k+1 distinct vertices x0, x1,···,xkdetermine a k-simplex of C(S)if and only if xiand xjare represented by two simple closed curves ciand cjon S such that ciintersects cjin just one point for each0≤i≠j≤k.

Let M be a compact orientable 3-manifold.If there is a closed surface S which cuts M into two compression bodies V and W such that S=∂+V=∂+W,then we say that M has a Heegaard splitting,denoted by M=V∪SW,where∂+V(resp.∂+W)means the positive boundary of V(resp.W).We denote by D(V)(resp.D(W))the set of vertices in C(S)such that each element of D(V)(resp.D(W))is represented by the boundary of an essential disk in V(resp.W).The distance of the Heegaard splitting V∪SW,denoted by d(S),is de fi ned to be dC(S)(D(V),D(W))(see[3]).

Hempel[3]showed that for any integers g≥2 and n≥2,there is a 3-manifold admitting a distance at least n Heegaard splitting of genus g.Similar results are obtained in di ff erent ways by[4–5].Minsky,Moriah and Schleimer[6]proved the same result for knot complements,and Li[7]constructed the non-Haken manifolds admitting high distance Heegaard splittings.In general,generic Heegaard splittings have Heegaard distances at least n for any n≥2(see[8–10]).By studying Dehn fi lling,Ma et al.[11]proved that distances of genus 2 Heegaard splittings cover all non-negative integers except 1.Recently,Ido et al.[12]proved that,for any n＞1 and g＞1,there is a compact 3-manifold with two boundary components which admits a distance n Heegaard splitting of genus g.Johnson[13]proved that there always exist closed 3-manifolds admitting a distance n≥5,genus g Heegaard splitting.Qiu et al.[14]proved that there is closed 3-manifold admitting any given distance, genus Heegaard splitting.

The main result of this paper is the following theorem∶

Theorem 1.1 Let n be a positive integer,{F1,···,Fn}be a collection of closed orientable surfaces,I⊂{1,2,···,n}and J={1,···,n}I be two subsets of{1,···,n}.Then,for any integers

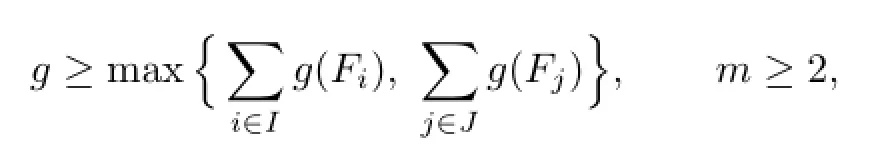
there is a compact 3-manifold M admitting a distance m Heegaard splitting of genus g,say M=V∪SW,such that

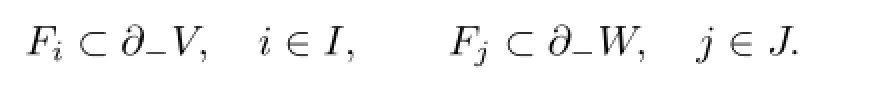
We introduce some results of curve complex in Section 2 and prove the main theorem in Section 3.

2 Some Results of Curve Complex

Let S be a compact surface of genus at least 1,and C(S)be the curve complex of S.We say that a simple closed curve c in S is essential if c bounds no disk in S and is not parallel to∂S.Hence each vertex of C(S)is represented by the isotopy class of an essential simple closed curve in S.For simplicity,we do not distinguish the essential simple closed curve c and its isotopy class c without any further notation.The following lemma is well known (see[2],[15–16]).

Lemma 2.1C(S)is connected,and the diameter ofC(S)is in fi nite.

We say that a collection G={a0,a1,···,an}is a geodesic in C(S)if each aiis contained in C0(S)and dC(S)(ai,aj)=|i−j|for any 0≤i,j≤n.The length of G is denoted by L(G) and de fi ned to be n.By the connection of C1(S),there is always a shortest path in C1(S) connecting any two vertices of C(S).Thus for any two vertices α and β of distance n,we call G={a0=α,···,an=β}a geodesic connecting α and β.Now for any two sub-simplicial complexes X,Y⊂C(S),we say that a geodesic G realizes the distance of X and Y if G connects an element α∈X and an element β∈Y such that L(G)=dC(S)(X,Y).

Let F be a compact surface of genus at least 1 with non-empty boundary.Similarly to the de fi nition of the curve complex C(F),we can de fi ne the arc and curve complex AC(F) as follows.

Each vertex of AC(F)is the isotopy class of an essential simple closed curve or an essential properly embedded arc in F,and a set of vertices forms a simplex of AC(F)if these vertices are represented by pairwise disjoint arcs or curves in F.For any two disjoint vertices,we place an edge between them.All the vertices and edges form a 1-skeleton of AC(F),denoted by AC1(F).And for each edge,we assign it length 1.Thus for any two vertices α and β in AC1(F),the distance dAC(F)(α,β)is de fi ned to be the minimal length of paths in AC1(F) connecting α and β.Similarly,we can de fi ne the geodesic in AC(F).

When F is a subsurface of S,we call that F is essential in S if the induced map of the inclusion from π1(F)to π1(S)is injective.Furthermore,we call that F is a proper essential subsurface of S if F is essential in S and at least one boundary component of F is essential in S.For more details the reader can see[16].

So if F is an essential subsurface of S,then there is some connection between AC(F)and C(S).For any α∈C0(S),there is a representative essential simple closed curve αgeosuch that the intersection number i(αgeo,∂F)is minimal.Hence each component of αgeo∩F is essential in F or S−F.Now for α∈C(S),let κF(α)be isotopy classes of the essential components of αgeo∩F.It is well de fi ned.

For any γ∈C(F),γ′∈σF(β)if and only if γ′is the essential boundary component of a closed regular neighborhood of γ∪∂F.Specially,let σF(∅)=∅.Now let πF=σF◦κF. Then the map πFlinks AC(F)and C(S),which is the de fi ned subsurface projection map in [16].

We say that α∈C0(S)cuts F if πF(α)≠∅.If α,β∈C0(S)both cut F,we write

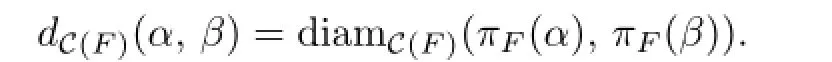
If dC(S)(α,β)=1,then dAC(F)(α,β)≤ 1 and dC(F)(α,β)≤ 2,observed by Masur and Minsky[16]at fi rst.What happens if the two vertices α and β have distance k in C(S)?

The following follows immediately from the above observation.

Lemma 2.2LetFandSbe as above,andG={α0,···,αk}be a geodesic ofC(S)such thatαjcutsFfor each0≤i≤k.Then

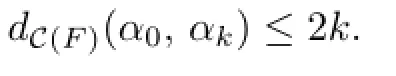
In general,Masur and Minsky[16]proved the following result called bounded geodesic image theorem.

Lemma 2.3LetFbe an essential sub-surface ofS,andγbe a geodesic segment inC(S),such thatπF(v)∅for every vertexvofγ.Then there is a constantMdepending only on

Ssuch that

When S is closed with g(S)≥2,there is always a compact 3-manifold M with S as its compressible boundary.Let D(M,S),called a disk set for S,be the subset of vertices of C(S), where each element bounds a disk in M.Now an essential simple closed curve on S,say c,is said to be disk-busting if S−c is incompressible in M.Since any two essential disks intersect in a typical way,it provides more information to study the subsurface projection of a disk complex.The following disk image theorem is proved by Li[17],Masur and Schleimer[18]independently.

Lemma 2.4LetMbe a compact orientable and irreducible3-manifold,and S be a boundary component ofM.Suppose that∂M−Sis incompressible.LetDbe the disk complex ofS,andF⊂Sbe an essential subsurface.Assume each component of∂Fis disk-busting.Then either

(1) Mis an I-bundle over some compact surface,Fis a horizontal boundary of the I-bundle and the vertical boundary of this I-bundle is a single annulus,or

(2)The image of this complex,κF(D),lies in a ball of radius3inAC(F).In particular,κF(D)has diameter6inAC(F).Moreover,πF(D)has diameter at most12inC(F).

Remark 2.1For any I-bundle J over a bounded compact surface P,∂J=∂vJ∪∂hJ, where the vertical boundary∂vJ is the I-bundle related to∂P,and the horizontal boundary∂hJ is the portion of∂J transverse to the I- fi bers.

Hempel[3]de fi ned a full simplex X on S to be a dimension 3g(S)−4 simplex in C(S). Hence,after attaching 2-handles and 3-handles along the vertices of X in the same side of S,we can get a handlebody,denoted by HX.

Lemma 2.5[3]LetSbe a closed,orientable surface of genus at least2.For any positive numberd,and for any full simplexXofC(S),there is another full simplexYofC(S)such that

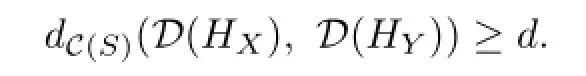
The central lemma in our proof is∶

Lemma 2.6([14],Lemma 2.6)Letg,n,m,s,tbe fi ve integers such thatg,m,n≥2,and1≤t,s≤g−1.LetSgbe a closed surface of genusg.Then there are two essential separating curvesαandβinSgsuch thatdC(Sg)(α,β)=n,one component ofSg−αhas genustwhile one component ofSg−βhas genuss.Furthermore,there is a geodesicG={a0=α,a1,···,an−1,an=β}inC(Sg)such that

(1)aiis non-separating inSgfor1≤i≤n−1,and

(2)mM+2≤dC(Sai)(ai−1,ai+1)=mM+6,whereSaiis the surfaceS−N(ai)for1≤i≤n−1.

3 The Proof of Theorem 1.1

Proof.Let S be a closed,orientable genus g surface.We assume that I∅.We choose F1(resp.F3)where 1∈I(resp.3∈J,when J∅)and g(F1)=t,g(F3)=s.If J=∅we choose s to be any positive number less than g(S).By Lemma 2.6,we can fi nd two essential separating slopes α and β on S such that one component of S1⊂S−N(α)(resp. S3⊂S−N(α))has genus t(resp.s)and dC(S)(α,β)=n,for any n≥3.Attaching 2-handles along α and β on S×I from di ff erent sides,we can get a Heegaard splitting V∪SW.And Heegaard distance of the Heegaard splitting is n,since in both V and W there is only one essential disk up to isotopy.It is not hard to see that one component of∂−V(resp.∂−W)has genus t(resp.S),denoted by F1(resp.F3).

Let Q1=F1and Q2be the components of∂−V,and S1and S2be the two components of S−α.Similarly,let Q3=F3and Q4be the components of∂−W,and S3and S4be the two components of S−β.Now B cuts V into two manifolds Q1×I and Q2×I,and D cuts W into two manifolds Q3×I and Q4×I.

We fi rst consider the compression body V.We may assume that

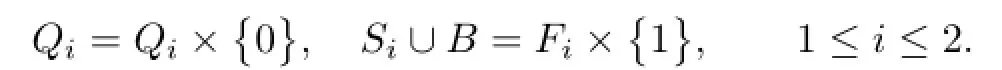
Let fQi∶Si∪B→Qibe the natural homeomorphism such that fQi(x×1)=x×0 for i=1,2 and fQi(∅)=∅.No doubt that fQiis well de fi ned.Then,for any two essential simple closed curves ζ,θ⊂Si∪B,i=1,2,

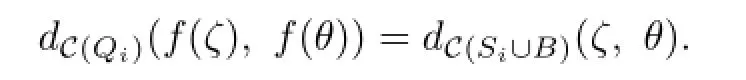
Hence fQiinduces an isomorphism from C(Si∪B)to C(Qi),for any i=1,2.Denote the isomorphism by fQitoo.

Let ι∶Si→Si∪B be the inclusion map for i=1,2.Note that∂Sicontains only one component.If c is an essential simple closed curve in Si,ι(c)is also essential in Si∪B. Now,for any two essential simple closed curves ζ,θ⊂Si,i=1,2,

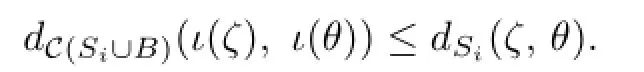
Hence ι induces a distance non-increasing map from C(Si)to C(Si∪B),for any i=1,2. Denote the inclusion map by ι too.Then we can de fi ne a projection map∶

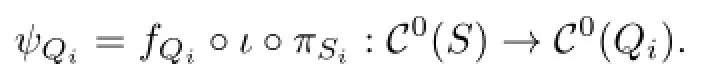
Since dC(S)(α,β)=n≥2,α∩β∅.By the argument in Section 2,

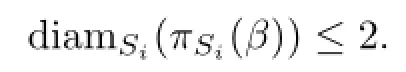
Hence

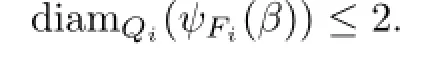
Let us consider the compression body V.Remember∂−V=Q1∪Q2.By Lemma 2.5, we can fi nd a full simplex X in Q2such that

It is not hard to see that we can choose some verticesΔof X such that after attaching 2-handles and possible 3-handles along these vertices,Q2×I is changed into a compression body C(Δ)and∂−(C(Δ))consists of{Fi,i∈I−{1}}.And V is changed into VC(Δ).Since D(C(Δ))⊂D(H(X)),

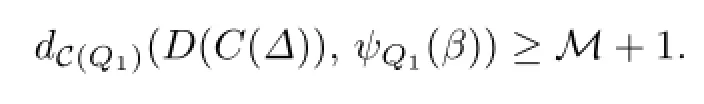
Claim 3.1The Heegaard distance of VC(Δ)∪SW is n.

Proof.Suppose,otherwise,that

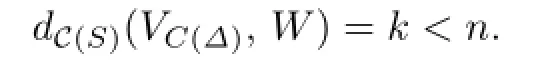
Since W contains only one essential disk D up to isotopy such that

there is an essential disk B1in VC(Δ)such that

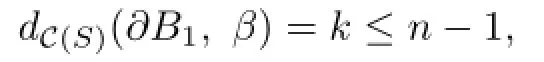
i.e.,there is a geodesic G={a0=β,···,ak=∂B1},where k≤n−1.

Fact 3.1aj∩S2∅for any 0≤j≤k.

Proof.Suppose that aj∩S2=∅for some 0≤j≤k.Since ak=∂B1and∂S2=α, ak∂S2.We say ak∩S2=∅for if not,then B1⊂Q1×I is an inessential disk of VC(Δ), which contradicts the choice of ak.Hence jk.j0 since a0=β.Hence there is a geodesic G∗={β=a0,···,aj,α}.It means that

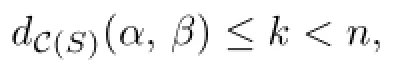
a contradiction.This completes the proof of Fact 3.1.

Let us continue to prove Claim 3.1.By Lemma 2.3 and Fact 3.1,

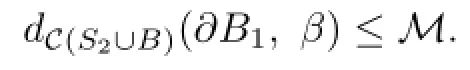
Furthermore,

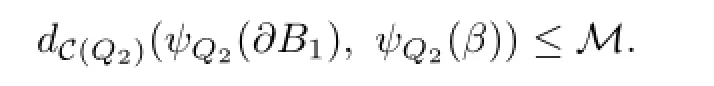
Depending on the way of intersection between B1and B,we have

(1)B1∩B=∅.Since B1is not isotopic to B,ψQ2(∂B1)bounds an essential disk in C(Δ).It contradicts the choice of X;

(2)B1∩B∅.Let a be an outermost arc of B1∩B on B1.It means that a,together with a sub-arc γ⊂∂B1,bounds a disk Bγsuch that Bγ∩B=a.Since B cuts VC(Δ)into a compression body C(Δ),which contains Q1and an I-bundle Q1×I,Bγ⊂C(Δ). Hence ψQ2(∂B1)bounds an essential disk in C(Δ).This contradicts the choice of X.So the distance of VC(Δ)∪SW is n.The proof of Claim 3.1 is completed.

∂−VC(Δ)consists of{Fi,i∈I}.Denote VC(Δ)by V.So∂−V consists of{Fi,i∈I}.

Now let us consider the compression body W.If J=∅,by Lemma 2.5,we can fi nd two full simplexes Z1⊂Q3and Z2⊂Q4such that

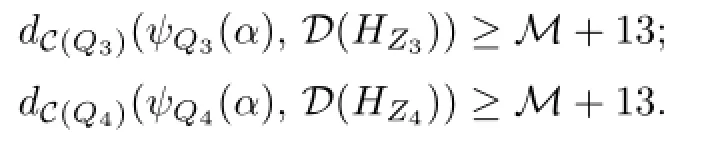
Then W is changed into WZ1,Z2.Denote WZ1,Z2by W.

Claim 3.2The Heegaard distance of V∪SW is n.

Proof.Suppose not.Then

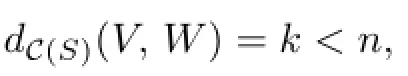
and there is an essential disk B1in V and an essential disk B2⊂W such that

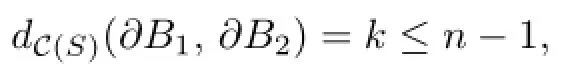
i.e.,there is a geodesic G={a0=∂B2,···,ak=∂B1},where k≤n−1.

Not hard to see that akβ.By the standard outermost disk argument,at least one of ψQ3(a0)and ψQ4(a0)is nonempty and bounds an essential disk in HZ3or HZ4.We assume that ψQ3(a0)∅and bounds an essential disk in HZ3.Hence ψQ3(a0)∈D(HZ3).On the other hand,by the proof of Fact 3.1,πS3(ai)∅,for any i⊂{0,1,···,k}.By Lemma 2.3,

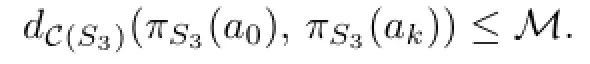
Hence

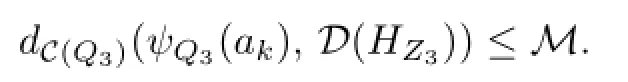
Let us consider the S3projection of the essential disk of V.Since Q1=F1⊂∂−V∅, V cannot be the I-bundle of any compact surface.By construction,∂S3=β intersects all the boundaries of essential disks in V.Then,by Lemma 2.4,

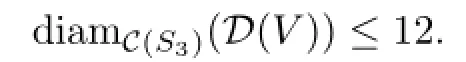
Hence

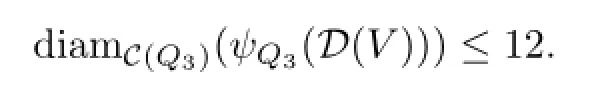
Since akbounds an essential disk in V,by the above argument,

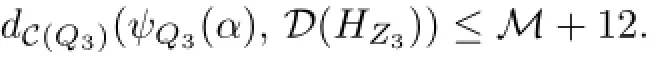
It contradicts the assumption

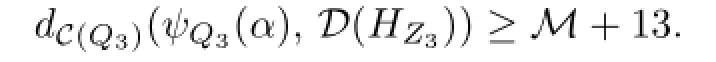
The argument for another case is similar.This completes the proof.

(1)∂+C(ζ)=Q4;

(2)∂−C(ζ)={Fj,j∈J−{3}};

(3)dQ4(D(C(ζ)),ψQ4(D(V)))≥M+1.

After attaching 2-handles along ζ to W,by the proof of Claim 3.2,the compression body W is changed into WC(ζ)and the Heegaard distance is n.Denote WC(ζ)by W.Then the Heegaard splitting V∪SW satis fi es the conclusions of our main theorem.

AcknowledgementWe thank Guo Qi-long for helpful discussions.

[1]Harvey W.Boundary Structure of the Modular Group.in:Riemann Surfaces and Related Topics:Ann.of Math.Stud.vol.97.Princeton,NJ:Princeton Univ.Press,1981:245–251.

[2]Masur H,Minsky Y.Geometry of the complex of curves I:Hyperbolicity.Invent.Math.,1999,138:103–149.

[3]Hempel J.3-manifolds as viewed from the curve complex.Topology,2001,40:631–657.

[4]Campisi M,Rathbun M.High distance knots in closed 3-manifolds.J.Knot Theory Rami fi cations,2012,21(2):Aticle ID 1250017,20pp.

[5]Evens T.High distance Heegaard splittings of 3-manifolds.Topology Appl.,2006,153:2631–2647.

[6]Minsky Y,Moriah Y,Schleimer S.High distance knots.Algebraic&Geom.Topology,2007,7: 1471–1483.

[7]Li T.Small 3-manifolds with large Heegaard distance.arXiv:1211.3064[math.GT].Submitted on 13 Nov.2012.

[8]Lustig M,Moriah Y.Horizontal Dehn surgery and genericity in the curve complex.arXiv: 0711.4492[math.GT].Submitted on 28 Nov.2007.

[9]Lustig M,Moriah Y.High distance Heegaard splittings via train tracks.Topology Appl.,2009,156(6):1118–1129.

[10]Lustig M,Moriah Y.Are large distance Heegaard splittings generic?J.Reine Angew.Math., 2012,670:93–119.

[11]Ma J,Qiu R.Degenerating slopes with respect to Heegaard distance.arXiv:0907.4419 [math.GT].Submitted on 25 July 2009.

[12]Ido A,Jang Y,Kobayashi T.Heegaard splittings of distance of exactly n.arXiv:1210.7627 [math.GT].Submitted on 29 Oct.2012.

[13]Johnson J.Non-uniquess of high distance Heegaard splittings.arXiv:1308.4599[math.GT]. Submitted on 21 Aug.2013.

[14]Qiu R,Zou Y,Guo Q.The Heegaard distances cover all non-negative integers.arXiv:1302. 5188[math.GT].Submitted on 21 Feb.2013.

[15]Minsky Y.A Geometric Approach to the Complex of Curves on A Surface.Finland:Proceedings of the Taniguchi Symposium,1995.

[16]Masur H,Minsky Y.Geometry of the complex of curves II:Hierarchical structure.Geom. Funct.Anal.,2000,10:902–974.

[17]Li T.Images of the disk complex.Geom.Dedicata,2012,158:121–136.

[18]Masur H,Schleimer S.The geometry of the disk complex.J.Amer.Math.Soc.,2013,26(1): 1–62.

tion:57M27

A

1674-5647(2014)03-0193-08

10.13447/j.1674-5647.2014.03.01

Received date:May 9,2013.

Foundation item:The NSF(11271058 and 11371076)of China.

*Corresponding author.

E-mail address:yanqing@mail.dlut.edu.cn(Zou Y Q),ximinliu@dlut.edu.cn(Liu X M).