Bifurcation in a Class of Planar Piecewise Smooth Systems with 3-parameters

(School of Mathematics,Jilin University,Changchun,130012)

Bifurcation in a Class of Planar Piecewise Smooth Systems with 3-parameters

LIU YUAN-YUAN AND CHAI ZHEN-HUA

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Ma Fu-ming

This paper is concerned with the bifurcation properties on the line of discontinuity of planar piecewise smooth systems.The existence of equilibria and periodic solutions with sliding motion in a class of planar piecewise smooth systems with 3-parameters is investigated in this paper using the theory of di ff erential inclusion and tools of Poincar´e maps.

piecewise smooth system,line of discontinuity,equilibria,periodic solution with sliding motion,bifurcation

1 Introduction

Many dynamical systems that occur naturally in the description of physical processes are presented as piecewise smooth equations.For example,they arise in the case of impacts, they occur in mechanical systems if the e ff ects of dry friction are considered,they frequently appear in control theory when discontinuous or impulse controls are involved(see[1–3]).

Piecewise smooth dynamical systems have been shown to exhibit many bifurcation phenomena that cannot be explained in terms of classical bifurcation theory for smooth systems. Examples include the bifurcation of equilibria of a planar piecewise smooth system when the discontinuity and the equilibria interact on each other(i.e.,equilibria lying on the discontinuity boundary of phase space),grazing bifurcation and sliding phenomenon etc.Bifurcation theories of smooth systems are well understood and described in many textbooks(see[4–6]), whereas bifurcations of systems with discontinuous vector fi elds(or Filippov systems)are still the object of active research.In[7],a procedure to fi nd all limit sets near bifurcatingequilibria was presented in a class of hybrid systems.Leine[8]showed a variety of bifurcation phenomena of equilibria which can be observed in non-smooth continuous systems. Giannakopoulos and Pliete[9]investigated the bifurcation of equilibrium points and periodic trajectories of Z2-symmetry planar piecewise linear di ff erential equations.Zanget al.[10]investigated the bifurcation properties of stationary points of a class of planar piecewise smooth systems with 3-parameters.

The focus of this paper is to investigate the bifurcation properties of stationary points on discontinuity and periodic solutions with sliding motion of a class of planar piecewise linear Filippov system with 3-parameters of the following form

In[10],the bifurcation properties of stationary points of the system(1.1)were well investigated under the restriction α+β−−α−β+=0.In this paper,we remove this restriction and investigate the existence theorems of stationary points on the line of discontinuity and periodic solutions with sliding motion.

This paper is organized as follows∶In Section 2,we introduce and discuss some basic assumptions and de fi nitions.In Section 3,we study the existence of equilibria on the line of discontinuity.In Section 4,we investigate the existence of periodic solutions with sliding motion by means of Poincar´e maps.

2 Basic Assumptions

In this section we introduce some basic assumptions for this work and discuss some consequences of our assumptions.We assume that

(H1)4det(A±)＞(tr(A±))20;

(H2)β±＞0;

(H3)α+β−−α−β+＞0.

Assumption(H1)implies that the matrices A+and A−possess a pair of complex eigenvalues a+±ib+and a−±ib−with a±0,respectively,that is to say the matrices A±are invertible.Assumption(H2)assures that the fl ow of the system(1.1)develops surrounding the origin clockwise.From assumption(H3)it follows that the vector fi eld on the line of discontinuityΣis quadratic rather than linear.

De fi ne

It is obvious that the vector fi elds f+and f−are tangent to the line of discontinuityΣat the points q+(λ)=(0,yq+(λ))and q−(λ)=(0,yq−(λ)),respectively,which means(q±(λ),λ)=0.Direct computation gives

De fi ne the function

which characterizes the directed distance between the tangent points q±(λ)and controls the existence and stability of the sliding motion solution of the equation(1.1).

De fi ne a set-valued function by

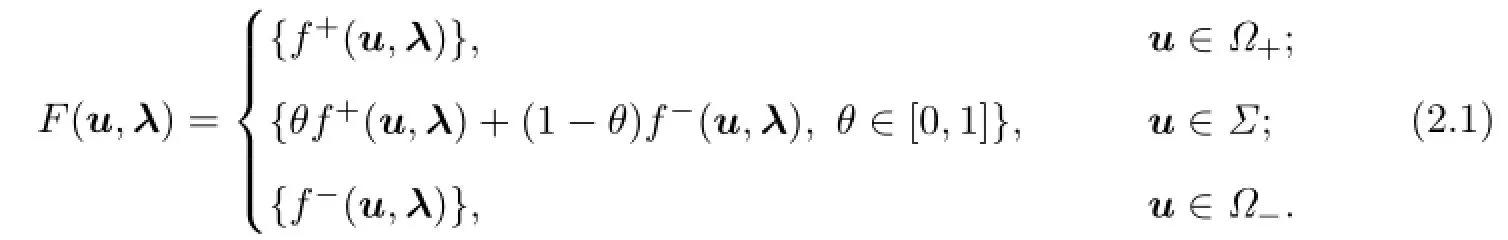
Apart fromΣ,the existence and uniqueness theorem ensures that the solutions of(1.1)are well de fi ned.We de fi ne the solutions of(1.1)nearΣby considering the following di ff erential inclusion

De fi nition 2.1[11]An absolutely continuous functionu(t)is called a solution of the equation(1.1),if it satis fi es the di ff erential inclusion(2.2)almost everywhere.

De fi nition 2.2A pointpis called a stationary point of(1.1),if0∈F(p,λ).

De fi nition 2.3A solution of the system(1.1)is called a sliding motion solution,if it or a part of it remains on the line of discontinuity Σ for at least a fi nite time.

De fi ne three sets on the y-axis

For any point u=(0,y)T∈M+,direct computation gives

Similarly,for any point u∈M−,we have

Therefore the sliding motion solution does not occur on M+∪M−.If φ(λ)=0,the set M contains a single point and the equation(1.1)does not have sliding motion solution.If φ(λ)0,together with assumption(H2),for any u=(0,y)T∈M,then we have

Therefore the sliding motion solution only occurs on M.If φ(λ)0 and u∈M.De fi ne

Direct computation gives

where

According to[11],on the line of discontinuity,a sliding solution u satis fi es the equation

Obviously,the dynamical behavior of the system(1.1)onΩ+∪Ω−is very clear.In this article we concentrate on discussing the existence of stationary points and periodic solutions with sliding motion on the line of discontinuity.

3 Equilibrium Points on the Line of Discontinuity

In this section we investigate the properties of the equilibrium points on the line of discontinuity.

Theorem 3.1Assume that(H1)–(H3)hold.There is no stationary point onM+∪M−of the equation(1.1).

Proof.According to the equations(2.1)and(2.3)–(2.5),it is obvious that F(u,λ)⊂(0,+∞)(resp.F(u,λ)⊂(−∞,0))for any u∈M+(resp.u∈M−).

Theorem 3.2Assume that(H1)–(H3)hold.Ifφ(λ)=0,then there is a unique stationary pointq+(λ)on the line of discontinuity Σ if and only ifλ2λ3≥0.

Proof.In the case of φ(λ)=0,we get q+(λ)=q−(λ).The vector fi eld F(q+(λ),λ) satis fi es

and

According to(H2),we have β±＞0 and+＞0.Therefore,u0is a stationary point if and only if,which is equivalent to λ2λ3≥0.This completes the proof.

Let

Direct computation gives

We have the following result.

Theorem 3.3Assume that(H1)–(H3)hold andφ(λ)0.

(1)IfΔ(λ)＜0,then there is no equilibrium point onM;

(2)IfΔ(λ)=0andH+(λ)H−(λ)＞0,then there is no equilibrium point onM;

(3)IfΔ(λ)=0andH+(λ)H−(λ)≤0,then there is only one stationary point onM;

(4)IfΔ(λ)＞0andλ2λ3＞0,then there is only one equilibrium point onM;

(5)IfΔ(λ)＞0,λ2λ3＜0,H+(λ)H−(λ)＜0andλ2φ(λ)＞0,then there are two stationary points onM;

(6)IfΔ(λ)＞ 0,λ2λ3＜ 0,H+(λ)H−(λ)＜ 0andλ2φ(λ)＜ 0,then there is no stationary point onM;

(7)IfΔ(λ)＞0,λ2λ3＜0andH+(λ)H−(λ)≥0,then there is no stationary point onM;

(8)IfΔ(λ)＞0,λ3=0andH−(λ)H0(λ)≤0,then there are two stationary points onM;

(9)IfΔ(λ)＞0,λ3=0andH−(λ)H0(λ)＞0,then there is only one stationary point onM;

(10)IfΔ(λ)＞0,λ2=0andH+(λ)H0(λ)≤0,then there are two stationary points onM;

(11)IfΔ(λ)＞0,λ2=0andH+(λ)H0(λ)＞0,then there is only one stationary point onM.

Proof.It is obvious that u=(0,y)T∈M is a stationary point of(1.1)if and only if f0(u,λ)=0,which is equivalent to g(y,λ)=0.Therefore,the proof follows from the properties of the solutions of the quadratic equation g(y,λ)=0 on M.

Firstly,we assume that yq−(λ)＜yq+(λ)and Fig.3.1 shows the di ff erent cases of the real solutions of the equation g(y,λ)=0 on[yq−,yq+].

Fig.3.1 The real solutions of the equation ay2+by+c=0 on interval[yq−,yq+]

If Δ(λ)＜0,the values of g(y,λ)are all positive for y∈[yq−,yq+],see Fig.3.1(a),then (1)is obviously true.

Because H±(λ)characterize the directed distance between h(λ)and q±(λ),it is obvious that H+(λ)H−(λ)＞0 if and only if h/∈[yq−,yq+]and H+(λ)H−(λ)≤0 if and only if h∈[yq−,yq+],see Fig.3.1(b)and(c),then(2)and(3)are obviously true.

At the points yq+(λ)and yq−(λ),direct computation gives

Together with(H2),it implies that g(h)g(yq+(λ))and λ2φ(λ)are opposite signs.According to Fig.3.1(d)–(g),(4)–(7)are obviously true.

In case of λ3=0,from(3.1),it follows that g(yq−(λ),λ)=0,then q−(λ)is a stationary point of the system(1.1)on M.Direct computation gives

This completes the proof of(8)–(9)by Fig.3.1(h)and(i).

By the similar way,λ2=0 implies g(yq+(λ),λ)=0 and q+(λ)is a stationary point of the system(1.1)on M.Direct computation gives

Likewise,we can get all assertions in the case of yq−(λ)＞yq+(λ).This completes the proof.

4 Periodic Solutions with Sliding Motion

In this section,we de fi ne two Poincar´e maps P+(·,λ1,λ2)and P−(·,λ1,λ3)on each half planeΩ+andΩ−,and discuss the existence of the periodic solution with sliding motion with the aid of Poincar´e maps.We assume that

(H4)α±＜0.

Assumption(H4)assures that if the system has an equilibrium point inΩ+orΩ−,then the equilibrium point is a stable focus.

If λ2≤0,for any initial point u0=(0,s)Twith s＞yq+(λ),then the solution fl ow of the equation˙u=f+(u,λ)transversal cross the line of discontinuityΣinto the right semi-plane x＞0 and intersect the line of discontinuity again at point(0,P+(s))within a fi nite time,see Fig.4.1(a).

Fig.4.1 The solution fl ow of the equation˙u=f+(u,λ)near the tangent point q+(λ)

De fi ne a Poincar´e map

such that(0,P+(s,λ1,λ2))T∈Σrepresents the fi rst crossing point of the solution fl ow of equation˙u=f+(u,λ)with initial value u0.Furthermore,the time map

represents the fl ight time of solution fl ow before intersect the line of discontinuityΣ.

If λ2＞0,then there is only one stationary point p+(λ)=(λ2,λ1)in the right semi-plane x＞0.For the initial value u0=q+(λ),the solution fl ow of the equation˙u=f+(u,λ) intersects the line of discontinuityΣat the point(0,(λ))Twith fi nite backward development of time and p+(λ)is the unique limit point of this fl ow with forward development of time,see Fig.4.1(b).Therefore,for any initial value(0,s)T∈Σwith s∈(yq+(λ),(λ)), the solution fl ow of the equation˙u=f+(u,λ)does not intersect the line of discontinuity in forward time development.Similarly,we can de fi ne the Poincar´e map

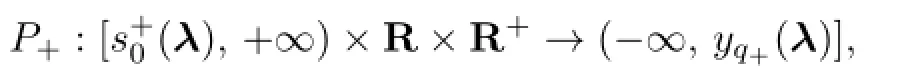
and the time fl ight map

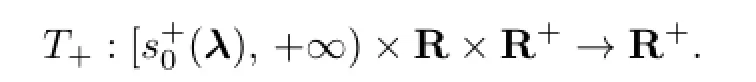
Similarly,we de fi ne the Poincar´e map P−(s,λ1,λ3)and the time fl ight map T−(s,λ1,λ3) by solving(1.1)onΩ−.If λ3≤0,see Fig.4.2(a),then we can de fi ne the Poincar´e maps.

If λ3＞0,see Fig.4.2(b),then we can de fi ne the Poincar´e maps

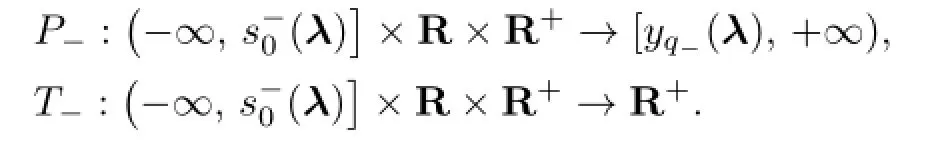
Fig.4.2 The solution fl ow of the equation=f-(u,λ)near the tangent point q-(λ)

The following two lemmas construct the Poincar´e maps and investigate its monotonicity.

Lemma 4.1[12]Assume that(H1)–(H2)hold.Ifλ2̸=0andλ1∈R,then one has the following formulas∶

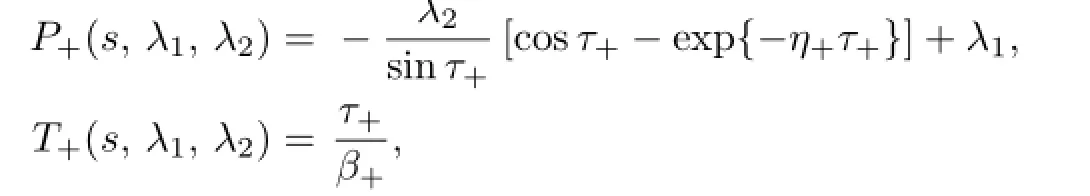
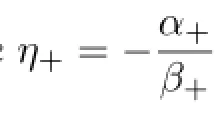
Ifλ2=0,for anyλ1∈Rands＞yq+(λ),then one has the following formulas∶

Furthermore,the Poincar´e mapsP+(s,λ1,λ2)(λ20)andP+(s,λ1,0)are both monotone decreasing functions in variables.

Lemma 4.2[12]Assume that(H1)–(H2)hold.Ifλ30andλ1∈R,then one has the following formulas∶

Ifλ3=0,for anyλ1∈Rands＜yq−(λ),then one has the following formulas∶

Furthermore,the Poincar´e mapsP−(s,λ1,λ3)(λ3̸0)andP−(s,λ1,0)are both monotone decreasing functions in variables.

De fi ne the sets

According to Theorem 3.3,if λ∈Ω1∪Ω2∪Ω6∪Ω7,then the system(2.2)has no stationary point on the line of discontinuityΣ.Let

The following two theorems introduce the existence of the periodic solution with sliding motion of(1.1)for λ∈Ω1∪Ω2∪Ω6∪Ω7.

Theorem 4.1Assume that(H1)–(H4)hold andλ∈Ω1∪Ω2∪Ω7.

(1)Ifφ(λ)≥0,then there is no periodic solution with sliding motion of the system(1.1);

(2)Ifφ(λ)＜0andλ3≤0,then there is no periodic solution with sliding motion of the system(1.1);

(3)Ifφ(λ)＜0,λ3＞0andQ−(λ)＜0,then there is only one periodic solution with sliding motion of the system(1.1);

(4)Ifφ(λ)＜0,λ3＞0,Q−(λ)=0andQ+(λ)＞0,then there are two periodic solutions with sliding motion of the system(1.1);

(5)Ifφ(λ)＜0,λ3＞0,Q−(λ)=0andQ+(λ)≤0,then there is only one periodic solution with sliding motion of the system(1.1);

(6)Ifφ(λ)＜0,λ3＞0,Q−(λ)＞0andQp(λ)＜0,then there is only one periodic solution with sliding motion of the system(1.1);

(7)Ifφ(λ)＜0,λ3＞0,Q−(λ)＞0andQp(λ)≥0,then there is no periodic solution with sliding motion of the system(1.1).

Proof.According to(2.3)–(2.5),the sliding motion solutions do not occur on M+∪M−. Therefore we only need to consider the case with the sliding motion solution on M.

If φ(λ)=0,then the set M degenerates into a point and(1.1)does not have sliding motion solution.If φ(λ)≠0,then according to Theorem 3.3 and Fig.3.1(a),(b)and(g) we obtain g(y,λ)＞0 for any u=(0,y)T∈M and λ∈Ω1∪Ω2∪Ω7.Therefore

Fig.4.3 The solution fl ow of(2.2)near the tangent points

If φ(λ)＜0,then the solution fl ow of(2.2)with the initial value u=(0,y)T∈M is an unstable movement along the line of discontinuity M,see Fig.4.4.

Fig.4.4 The solution fl ow of(2.2)near the tangent points q+(λ)and q-(λ)for φ(λ)＜0

Therefore,the solution fl ows of(2.2)in two semi-planes enter into the line of discontinuity M only at the tangent points q+(λ)and q−(λ).According to(4.1),we have(u,λ)＜0 for any u=(0,y)T∈M and λ∈Ω1∪Ω2∪Ω7which means that the solution fl ow of (2.2)with the initial value u=(0,y)T∈M is an unstable downward movement along the line of discontinuity M.Then the periodic solution of(2.2)with sliding motion enter into the line of discontinuity M only at the tangent point q−(λ).If λ3≤0,then we get P−(u,λ)＞yq−(λ)for all u＜yq−(λ)(see Fig.4.5(a)).Therefore the solution fl ow cannot go back to the tangent point q−(λ)and(2)is obviously true.

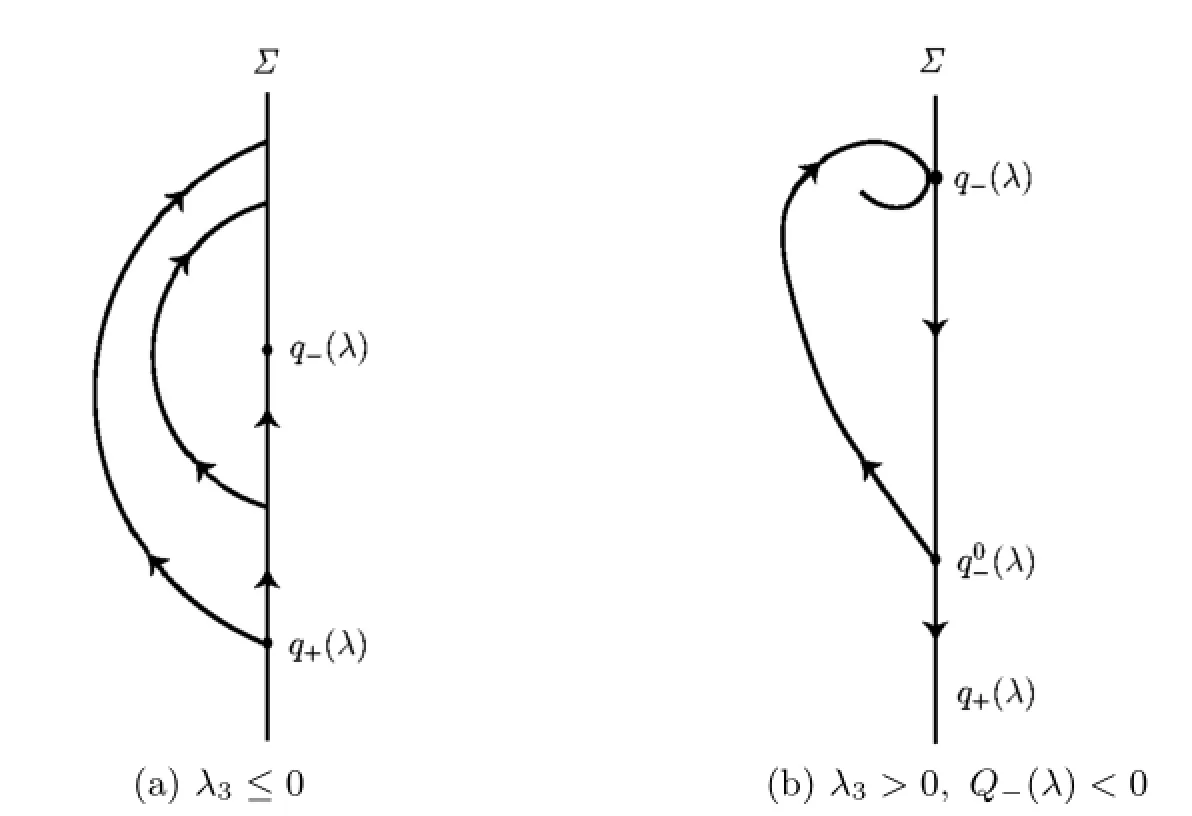
Fig.4.5 The solution fl ow of(2.2)near the tangent points q+(λ)and q-(λ) for φ(λ)＜0 and λ∈Ω1∪Ω2∪Ω7

see Fig.4.5(a)and we get(4).

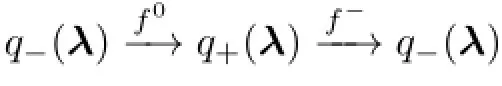
If φ(λ)＜0,λ3＞0,Q−(λ)＞0 and Qp(λ)≥0,then there is no periodic solution with sliding motion,see Fig.4.6(b)–(c)and(7)is true.

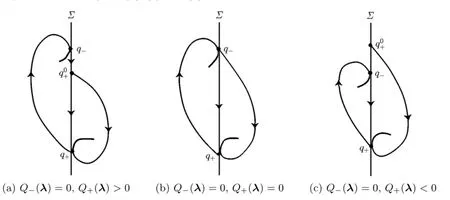
Fig.4.6 The solution fl ow of(2.2)near the tangent points q+(λ)and q-(λ) for φ(λ)＜0,λ3＞0 and λ∈Ω1∪Ω2∪Ω7

Theorem 4.2Assume that(H1)–(H4)hold andλ∈Ω6.

(1)Ifλ2＜0,then there is no periodic solution with sliding motion of the system(1.1);

(2)Ifλ2＞0andQ+(λ)≥0,then there is only one periodic solution with sliding motion of the system(1.1);

(3)Ifλ2＞0,Q+(λ)＜0andQq(λ)＜0,then there is only one periodic solution with sliding motion of the system(1.1);

(4)Ifλ2＞0,Q+(λ)＜0andQq(λ)≥0,then there is no periodic solution with sliding motion of the system(1.1).

Proof.According to Theorem 3.3 and Fig.3.1(f)we obtain g(y,λ)＜0 for any u= (0,y)T∈M and λ∈Ω6.Therefore

According to the de fi nition ofΩ6,if λ2＜0 and λ∈Ω6,then λ3＞0,φ(λ)＞0 and(u,λ)＜0.Therefore,the solution fl ow of(2.2)with the initial value u=(0,y)T∈M is a stable downward movement along the line of discontinuity M,see Fig.4.7(b).Therefore, the solution fl ow of(2.2)with the initial value u=(0,y)T∈M leaves away from the line of discontinuity M only at the tangent point q−(λ)and goes into the left semi-plane x＜0.According to the assumption(H4),it is obvious that the solution fl ow and the line of discontinuityΣare no longer intersecting as the time forward develop.Therefore,there is no periodic solution with sliding motion of the system(2.2)and the assertion(1)is true.

If λ2＞0 and λ∈Ω6,then λ3＜0,φ(λ)＜0 andTherefore,the solution fl ow of(2.2)with the initial value u=(0,y)T∈M is a unstable upward movement along the line of discontinuity M,see Fig.4.7(b).Therefore,the solution fl ow of(2.2)with the initial value u=(0,y)T∈M enters into the line of discontinuity M only at the tangentpoint q+(λ).If Q+(λ)＞0,then(λ)＜yq−(λ)and the solution fl ows construct a periodic solution with sliding motion along the following path(see Fig.4.8(a))

For the case of Q+(λ)=0,the proof is similar and(2)is obviously true.

Fig.4.7 The solution fl ow of(2.2)near the tangent points q+(λ)and q-(λ) for φ(λ)＜0,λ3＞0 and λ∈Ω1∪Ω2∪Ω7

Fig.4.8 The solution fl ow of(2.2)near the tangent points q+(λ)and q-(λ) for φ(λ)＜0,λ2＞0,λ3＜0 and λ∈Ω6

(3)is obviously true.Similarly,(4)is obviously true by Fig.4.8(c)–(d).

[1]Bernardo M Di,Feigin M I,Hogan S J,Homer M E.Local analysis of C-bifurcations in n-dimensional piecewise-smooth dynamical systems.Chaos Solitons Fractals,1999,10:1881–1908.

[2]Kunze M.Non-smooth Dynamical Systems.vol.1744.Berlin:Springer-Verlag,2000.

[3]Zou Y K,K¨upper T.Generalized Hopf bifurcation emanated from a corner for piecewise smooth planar systems.Nonlinear Anal.,2005,62:1–17.

[4]Guckenheimer J,Holmes P H.Nonlinear Oscillations,Dynamical Systems,and Bifurcations of Vector Fields.in:Appl.Math.Sci.vol.42.New York:Springer-Verlag,1983.

[5]Kuznetsov Y A.Elements of Applied Bifurcation Theory.in:Appl.Math.Sci.3rd ed.vol.112. New York:Springer-Verlag,2004.

[6]Seydel R.Practical Bifurcation and Stability Analysis.in:Interdisciplinary Applied Mathematics.2nd ed.vol.5.New York:Springer-Verlag,1994.

[7]Benjamin Biemond J J,Nathan van de W,Henk N,Nonsmooth bifurcations of equilibria in planar continuous systems.Nonlinear Anal.,2010,4:451–474.

[8]Leine R I.Bifurcations of equilibria in non-smooth continuous systems.Phys.D,2006,223: 121–137.

[9]Giannakopoulos F,Pliete K.Planar systems of piecewise linear di ff erential equations with a line of discontinuity.Nonlinearity,2001,14:1611–1632.

[10]Zang L,Chen X M,Gong C C,Zou Y K.Bifurcation of equilibria in a class of planar piecewise smooth system with 3-parameters.Comm.Math.Res.,2009,25:204–212.

[11]Filippov A F.Di ff erential Equations with Discontinuous Righthand Sides.in:Math.Appl. (Soviet Ser.).vol.18.Translated from the Russian.Dordrecht:Kluwer Academic Publishers Group,1988.

[12]Zang L.Analysis of Local Bifurcation and Generalized Hopf Bifurcation for a Class of Filippovtype Systems(in Chinese).Ph.D Thesis.Changchun:Jilin Univ.,2008.

tion:34A36,34A60,34C23,37G10

A

1674-5647(2014)03-0207-15

10.13447/j.1674-5647.2014.03.03

Received date:Sept.15,2011.

Foundation item:The NSF(11071102)of China.

E-mail address:yyliu09@mails.jlu.edu.cn(Liu Y Y).