Boundedness for Commutators of Approximate Identities on Weighted Morrey Spaces

ZHANG LEI,ZHENG QING-YU AND SHI SHAO-GUANG

(School of Sciences,Linyi University,Linyi,Shandong,276005)

Boundedness for Commutators of Approximate Identities on Weighted Morrey Spaces

ZHANG LEI,ZHENG QING-YU AND SHI SHAO-GUANG*

(School of Sciences,Linyi University,Linyi,Shandong,276005)

Communicated by Ji You-qing

The aim of this paper is to set up the weighted norm inequalities for commutators generated by approximate identities from weighted Lebesgue spaces into weighted Morrey spaces.

approximate identity,weighted Morrey space,weighted BMO space, commutator

1 Introduction

Suppose that φ∈L1(Rn),f∈Lp(Rn)(1≤p＜∞)and φε(x)=ε−nφ(ε−1x)for all ε＞0. If the operator

then as ε→0,φεis called the kernel of approximate identities on Lp(Rn),and Tφis called the operator of approximate identities.If φεfurther satis fi es

Franciaet al.[1]have proved that Tφis bounded from Lp(Rn)into Lp(Rn)with 1＜p＜∞.

Recall the de fi nitions of Muckenhoupt classes(see[2])∶

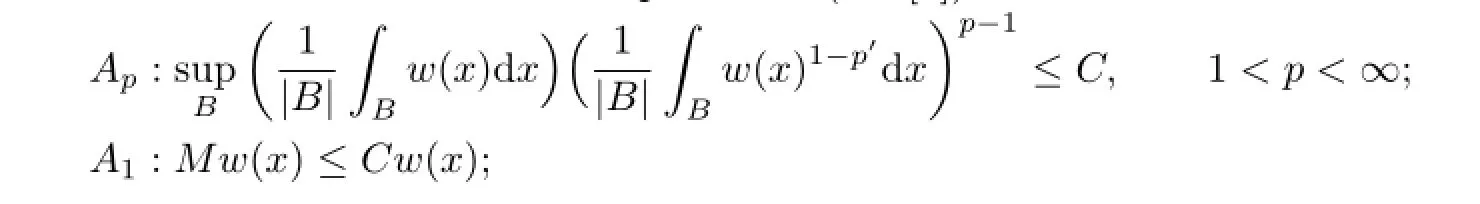
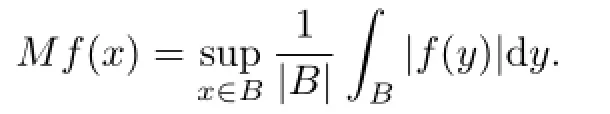
For a measure ν,we say w(x)∈Ap(ν)if

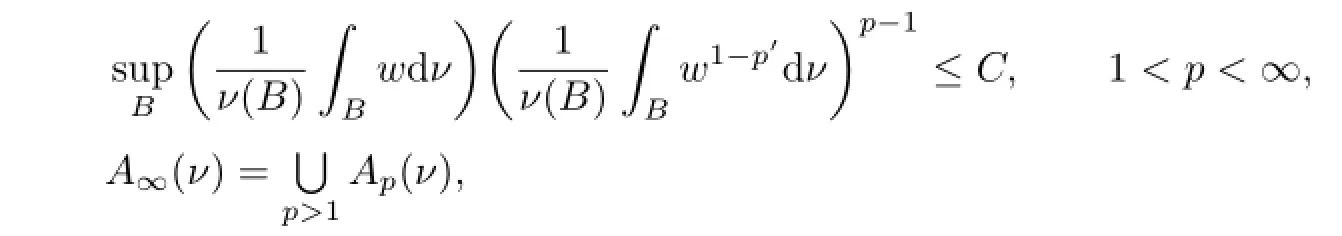
For w∈Ap,the weighted BMO space is de fi ned by

To investigate the local behavior of solutions to the second order elliptic partial di ff erential equations,Morrey[4]fi rst introduced the classical Morrey space Mp,q(Rn)with the norm

For some earlier work on Mp,q(Rn),see,e.g.,[5–6].For a recent account of the theory on the general case of Mp,q(Rn),we refer the reader to[7–9].Mp,q(Rn)is a natural expansion of Lp(Rn)in the sense that Mp,p(Rn)=Lp(Rn).

Komori and Shirai[10]introduced the weighted Morrey space,which is a natural generalization of the weighted Lebesgue space.Let 1≤p＜q＜∞and w1,w2be two functions. Then the norm of the weighted Morrey space Mp,q(w1,w2)is de fi ned by

If w1=w2=w,we denote Mp,q(w1,w2)=Mp,q(w).It is obvious that Mp,0(w)=Lp(w) and Mp,1(w)=L∞(w).

Inspired by[3,10],we establish the weighted estimates for Tφ,bon Mp,k(w).

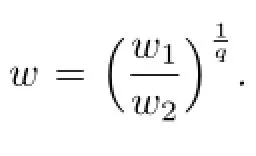
2 Preliminaries

For any B⊂Rn,the sharp Hardy-littlewood maximal function is given by

It was proved in[2]that Mwis bounded on Lp(w)if 1＜p＜∞and w∈Ap.Now,we state the well known sharp function theorem which fi rst introduced by Bloom[11].

Lemma 2.1[11]Letf∈L1(dν),1＜p＜∞andM♯f∈Lp(w)for somew∈A∞(dν).Thenf∈Lp(w)with

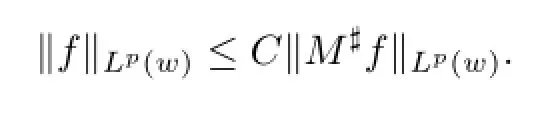
Using Lemma 2.1,we can easily obtain the following weighted BMO theorem.

Lemma 2.2[11]LetB=B(x0,r)be a ball andBk=2kB=B(x0,2kr).Then ifb∈BMO(w)withw∈Ap,we have

where

Proof.w∈Apand the reverse H¨older’s inequality yield that there exists an ε＞0,for any fi xed ball B⊂Rn,we have

that is,

which implies that

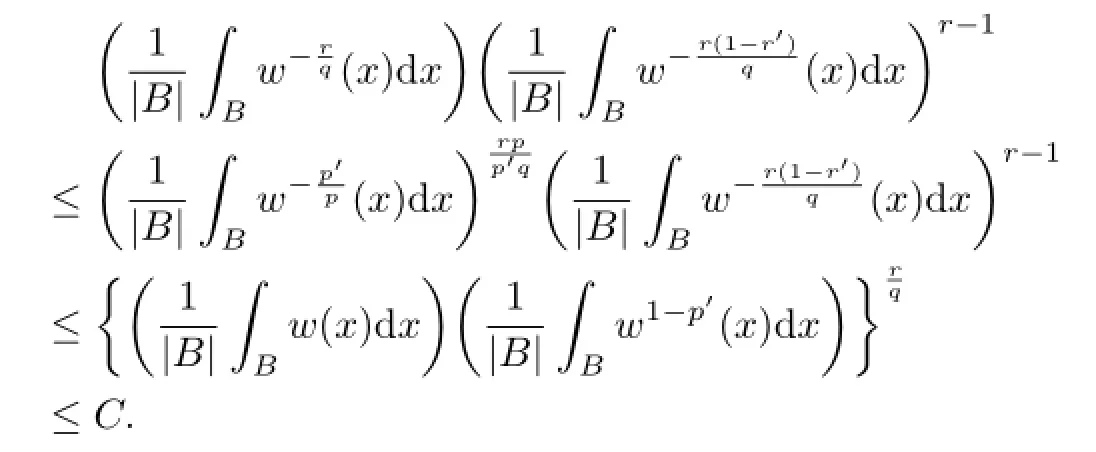
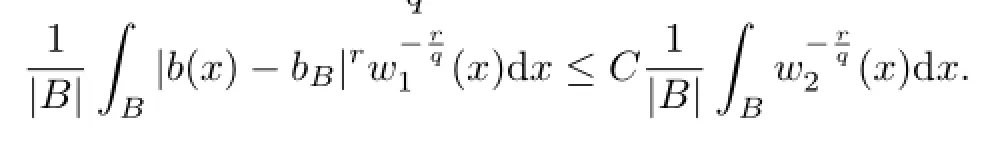
Proof.Since b∈BMO(w),we can obtain that

which yields that

By Lemma 2.3,(2.1)and the Lp(w)boundedness of M,we get

which is the desired result.Similar analysis see,e.g.,Corollary 2.2 of[11].

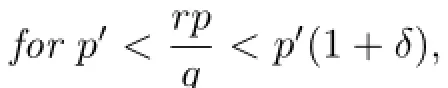
Proof.We fi rst claim that

Indeed,by H¨older’s inequality,we have

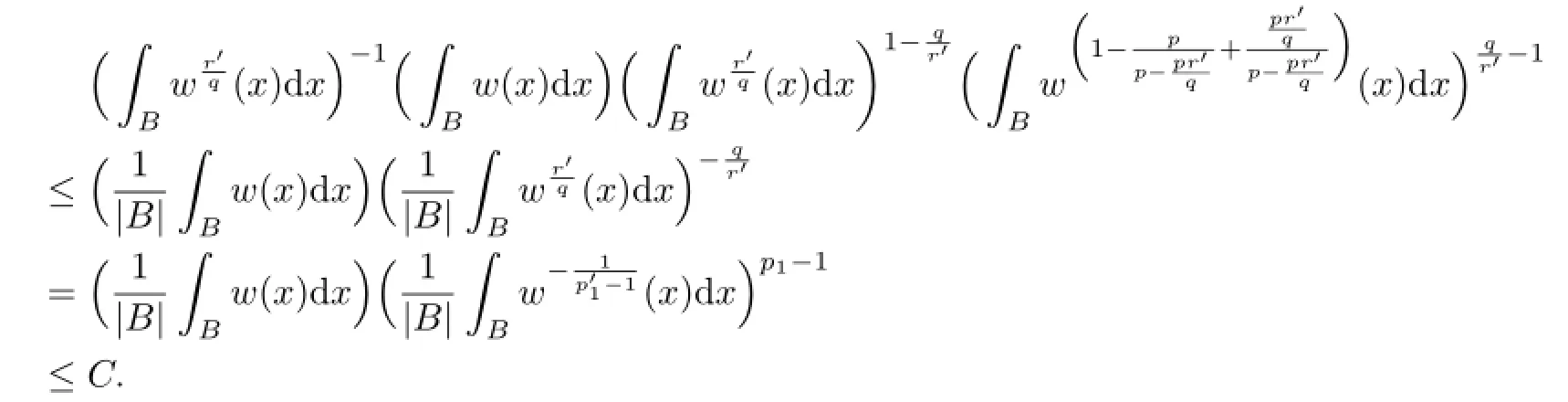
By the reverse H¨older’s inequality,we get Lemma 2.5.

Lemma 2.6[3]Under the same condition as in Theorem1.1,Tφ,bis bounded fromLp(w1)intoLp(w2).

3 Proofs of the Main Results

Proof of Theorem 1.1The proof of Theorem 1.1 depends heavily on the following proposition.

Proof.Let B=B(x0,r)denote the ball with center at x0and radius r,J=8B= B(x0,8r).Given a function f with compact support,we set

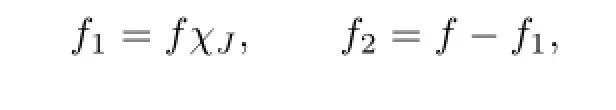
and

For x∈B,noting

we have

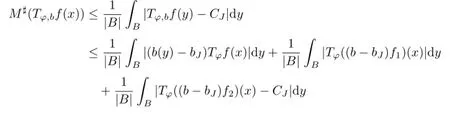
By H¨older’s inequality and Lemmas 2.3–2.4,

By the similar analysis,we can obtain

Now,we come to deal with the term III.Applying(1.1)to III,we obtain

Similar arguments as those of II give

On the other hand,applying Lemma 2.2 to the term III2yields

The proof of Proposition 3.1 is completed.

We are now in a position to show the proof of Theorem 1.1.By Proposition 3.1,we have

Lemma 2.5 and H¨older’s inequality imply

In the same manner,we can obtain that

and

Theorem 1.1 is a by-product of the above estimates for J,JJ and JJJ.

Proof of Theorem 1.2.Theorem 1.2 is a straightforward result of Lemma 2.6.In fact,

This completes the proof.

[1]Rubio de Francia J,Ruiz J,Torrea F.Calder`on-Zygmund theory for operator-valued kernels. Adv.Math.,1986,62:7–48.

[2]Garcia-Cuerva J,Rubio de Francia J.Weighted Norm Inequalities and Related Topics.North-Holland:Amsterdam,1985.

[3]Segovia C,Torrea J.Vector valued commutators and applications.Indiana Univ.Math.J., 1989,38:959–971.

[4]Morrey C.On the solutions of quasi-linear elliptic partial di ff erential equations.Trans.Amer. Math.Soc.,1938,43:126–166.

[5]Adams D.A note on Riesz potentials.Duke Math.J.,1975,42:765–778.

[6]Chiarenza F,Frasca M.Morrey spaces and Hardy-Littlewood maximal function.Rend.Math. Appl.,1987,7(7):273–279.

[7]Duong X,Xiao J,Yan L.Old and new Morrey spaces with heat kernel bounds.J.Fourier Anal.Appl.,2007,13:87–111.

[8]Lin H,Nakai H,Yang D.Boundedness of Lusin-area and g∗λfunctions on localized Morrey-Campanato spaces over doubling metric measure spaces.J.Funct.Spaces Appl.,2011,9(3): 245–282.

[9]Nakai E.The Cmapanato,Morrey and H¨older spaces on spaces of homogeneous type.Studia Math.,2006,176:1–19.

[10]Komori Y,Shirai S.Weighted Morrey spaces and a singular integral operator.Math.Nachr., 2009,282:219–231.

[11]Bloom S.A commutator theorem and weighted BMO.Trans.Amer.Math.Soc.,1985,292: 103–122.

tion:42B20,42B25

A

1674-5647(2014)03-0257-08

10.13447/j.1674-5647.2014.03.07

Received date:Jan.26,2012.

Foundation item:This work was partially supported by the NSF(11271175)of China and the NSF (ZR2012AQ026)of Shandong Province.

*Corresponding author.

E-mail address:zhanglei-0335@163.com(Zhang L),shishaoguang@lyu.edu.cn(Shi S G).