Stationary Solutions for a Generalized Kadomtsev-Petviashvili Equation in Bounded Domain

(1.Department of Mathematics,Qilu Normal University,Jinan,250013)

(2.School of Mathematics,Shandong University,Jinan,250100)

Stationary Solutions for a Generalized Kadomtsev-Petviashvili Equation in Bounded Domain

ZHANG KE-YU1,2AND XU JIA-FA2

(1.Department of Mathematics,Qilu Normal University,Jinan,250013)

(2.School of Mathematics,Shandong University,Jinan,250100)

Communicated by Li Yong

In this work,we are mainly concerned with the existence of stationary solutions for a generalized Kadomtsev-Petviashvili equation in bounded domain ofRn.We utilize variational method and critical point theory to establish our main results.

generalized Kadomtsev-Petviashvili equation,stationary solution,critical point theory,variational method

1 Introduction

We investigate the stationary solutions for the generalized Kadomtsev-Petviashvili equation in bounded domain ofRnas follows∶

where λ is a parameter,Ω⊂Rnis a bounded domain with smooth boundary,

denotes the inverse operator,

and

In this paper,we utilize variational methods and some critical point theorems to study the stationary solutions for the generalized Kadomtsev-Petviashvili equation(1.1).

In mathematics and physics,the Kadomtsev-Petviashvili equation(KP equation),named after Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili,is a partial di ff erential equation to describe nonlinear wave motion.To the best of our knowledge,by virtue of variational method and critical point theory,the recent papers on the subject can be found in[1–7]and the references therein.Generally,it reads

where

where c＞0 is fi xed.Liang and Su[1]considered the case that the non-constant weight function for generalized Kadomtsev-Petviashvili equation,and Xuan[2]dealt with the case, where N ≥2 and f(u)satis fi es some superlinear conditions.Their main tool in[1–2] is the famous Ambrosetti-Rabinowitz mountain pass theorem.Wang and Willem[3]built multiplicity results of solitary waves of(1.2)by Lyusternik-Schnirelman theory.He and Zou[4]established the existence of nontrivial solitary waves for(1.1)(the case λ=0)by Szulkin and Zou’s linking theorem.More precisely,in[4],f(u)is required to satisfy the following conditions∶

moreover,

(ii)There exists a v0∈Y={ux∶u∈C∞0(RN)}such that

(iv)uf(u)≥0 for all u∈R.

Under the above conditions,(1.1)possesses a nontrivial solution(see Theorem 1.1 in [4]).Note that the Ambrosetti-Rabinowitz type superlinear condition is crucial in proving the boundedness of the Palais-Smale sequence(see(f3)of page 16 in[2]).However,in[4],there is no need for(iii)to satisfy the Ambrosetti-Rabinowitz type superlinear condition. Clearly,it becomes more complicated for obtaining a bounded Palais-Smale sequence,and hence this paper has generalized and improved the results due to Xuan[2].

In this paper,we fi rst establish the eigenvalue theory for generalized KP equation.Then we get our main results as follows∶for the case λ=0,by virtue of the conditions involving the fi rst eigenvalue,the existence theorem is obtained by the least action principle.For the case λ=λk(where λkdenotes the relevant eigenvalues for the generalized KP equation, k=1,2,···),we use the saddle point theorem to obtain a result with the existence of weak solution for(1.1)under the famous Ahmad-Lazer-Paul condition(see[8]).Our methods adopted here are di ff erent from those of[1–7]due to the intervention of the eigenvalues and eigenfunctions.

2 Preliminaries

ForΩ⊂Rnis a bounded domain with smooth boundary∂Ωon Y∶={gx∶g∈we de fi ne the inner product

where

and the corresponding norm

A function u∶Ω→Rbelongs to X,if there exists⊂Y such that

(1)um→u a.e.onΩ;

(2)‖uj−uk‖→0 as j,k→∞.

Note that the space X with the inner product(2.1)and the norm(2.2)is a Hilbert space (see[1–2]).We know that the exponent

is as critical as the critical Sobolev exponent

i.e.,there exists a constant C＞0 such that the estimate

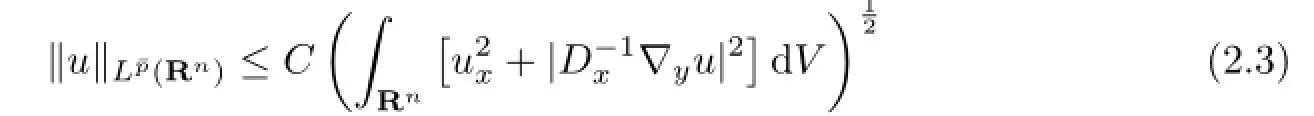
From the interpolation theorem,the boundedness ofΩand estimate(2.3),there is an embedding theorem about X as follows.

Lemma 2.1[6]The embedding from the space(X,‖·‖)into the space(Lp(Ω),‖·‖p)is compact for1≤p＜

By Lemma 2.1,there exists a τp＞0 such that

where

In what follows,we establish the energy functional for(1.1).Note that we can rewrite(1.1) in the following form(see[6])∶

For each v∈X,multiplying the both sides of the above equation in(2.5)by v(x,y)and integrating overΩ,we obtain

By using Green formula and integrating(2.6)by parts,we have

Therefore,on X,we de fi ne a functional J as

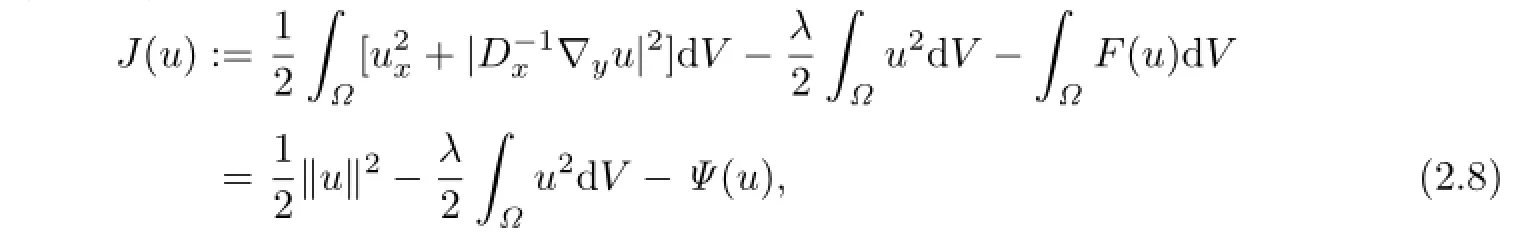
where

For the nonlinearity of f,we always assume that it satis fi es the following condition∶

Lemma 2.2[6]Let(H1)hold.ThenJ∈C1(X,R),moreover,

and critical points ofJonXare the weak solutions of(1.1).

Lemma 2.3[9]LetA∶X → Xbe a compact,selfadjoint and positive linear operator from an in fi nite dimensional separable real Hilbert spaceXinto itself.Then all eigenvalues ofAare positive reals and there exists an orthonormal basis ofXwhich consists of the eigenvectors ofA.If,moreover,µ1≥µ2≥···＞0,µn→0(n→∞),denote the eigenvalues ofA,then

and

µk+1=max{(Au,u)∶‖u‖=1,(u,v1)=···=(u,vk)=0}, k=1,2,···

Remark 2.1A linear operator A is said to be selfadjoint and positive if

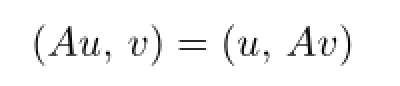
and

In what follows,we fi rst consider the eigenvalue problem

By a computation similar to those of(2.6)and(2.7),we get

if u∈X satis fi es(2.12).

The operator A∶X→X is de fi ned by

Then it is obvious that A is selfadjoint and positive.Furthermore,A is compact by Lemma 2.1.Note that X is a Hilbert space of in fi nite dimensions(see[2]).Therefore,from Lemma 2.3 we know that all eigenvalues of A are positive reals and there exists an orthonormal basis of X which consists of the eigenvectors of A.Consequently,ifdenote the eigenvalues of A,thenµ1≥µ2≥···＞0 for the fact thatµnare all positive reals for n=1,2,···By Corollary 2.2.13 of[9]and dimX=∞,we fi nd that 0 is an accumulation point of σ(A),i.e.,µn→∞as n→∞.Lemma 2.3 enables us to get

and

µk+1=max{(Au,u)∶‖u‖=1,(u,v1)=···=(u,vk)=0}, k=1,2,···

Let φnbe the eigenfunction associated withµnand λn∶=for n=1,2,···in the sequel.

Then λ1≤λ2≤···λn≤···and λn→+∞as n→∞,moreover,

We utilize the critical point theory to prove our main results.Let us collect some de fi nitions and lemmas that would be used later.One can refer to[7],[9–11]for more details.

Lemma 2.4LetXbe a Hilbert space.Suppose that a functionalJ∶X→Ris

(1)weakly lower semi-continuous(weakly l.s.c);

(2)coercive(i.e.,J(u)→+∞as‖u‖→∞).

ThenJis bounded from below and there exists au0∈Xsuch that

Lemma 2.5LetJ∈C2(X,R)andX=Y⊕Z,wheredimY＜∞andZis a closed subspace ofX.Moreover,assume that there is aϱ＞0,denoting

such that

Let

where

IfJsatis fi es(PS)ccondition(see[11]),thencis a critical value ofJ.

3 Main Results

For the case λ=0,our one main result is as follows∶

Theorem 3.1If(H1)holds and the following assumption is satis fi ed∶

(H2)there exists anα＜λ1such that

then(1.1)has a weak solution inX.

Proof.Our working space X is a Hilbert space(see[1–2]).By Lemma 3.1 in[6],we see that J is weakly lower semi-continuous on X.On the other hand,(H2)and I’Hˆospital’s rule imply

and hence,taking α1with α＜α1＜λ1,we can fi nd M1such that

Furthermore,(H1)gives

Therefore,

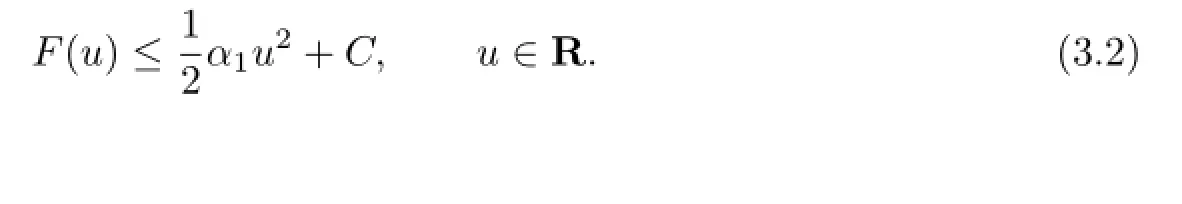
By the de fi nition of J and(3.2),we have

Since

we can conclude that J is coercive on X.Lemma 2.4 yields that there exists a u0∈X such that

i.e.,u0is a critical point of J.Equivalently,(1.1)has a weak solution.This completes the proof.

For the case λ=λk,our another main result is as follows∶

Theorem 3.2Suppose that(H1)holds.Letfandbe bounded and continuous.If,moreover,the following assumption is satis fi ed∶

Proof.For the reason that λ=λk,the energy functional associated with(1.1)is

which has the property J∈C2(X,R)due to the assumptions on f andIndeed,by direct computation,we have

Let

and

Then

i.e.,

Step 1.We prove that J has a geometry of the saddle point theorem.If u∈Z,then

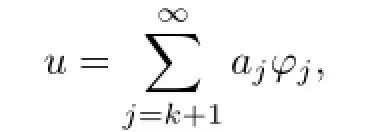
where aj(j=k+1,k+2,···)are constants and

Note that f is bounded and let

Then we have

by H¨older’s inequality and Lemma 2.1.Combining(3.7)and(3.8)shows that J is bounded below on Z,i.e.,

Next,if u∈Y,then u=u0+where

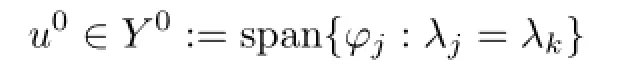
and

and

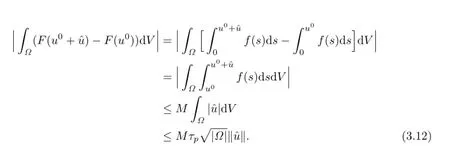
It follows from(3.10)–(3.12)that

This implies that

Step 2.Now we prove that J satis fi es the(PS)ccondition.Assume that|J(um)|≤K for some K＞0 and→0.We can write

For a large m,we have

and similarly to(3.15),we can getOn the other hand,since Z=Y⊥,by(3.7),(3.15) and the boundedness of f,we obtain

(3.15)and(3.16)enable us to fi nd that

By(3.12)and

and

As a result,(3.17)holds,as required.

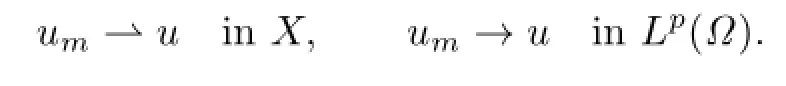
Then

But we also have

Together with(3.18)and(3.19),we fi nd

i.e.,

This prove that J satis fi es the(PS)ccondition.This completes the proof.

Remark 3.1(1)Let

Then it satis fi es the conditions(H1)and(H2).

(2)Let

Then

and

[1]Liang Z P,Su J B.Existence of solitary waves to a generalized Kadomtsev-Petviashvili equation.Acta Math.Sci.,2012,32B:1149–1156.

[2]Xuan B J.Nontrival solitary waves of GKP equation in multi-dimensional spaces.Rev.Colombiana Mat.,2003,37:11–23.

[3]Wang Z Q,Willem M.A multiplicity result for the generaligned Kadomtsev-Petviashvili equation.Topol.Methods Nonlinear Anal.,1996,7:261–270.

[4]He X M,Zou W M.Nontrivial solitary waves to the generalized Kadomtsev-Petviashvili equations.Appl.Math.Comput.,2008,197:858–863.

[5]Zou W M.Solitary waves of the generalized Kadomtsev-Petviashvili equations.Appl.Math. Lett.,2002,15:35–39.

[6]Xu J F,Wei Z L,Ding Y Z.Stationary solutions for a generalized Kadomtsev-Petviashvili equation in bounded domain.Electron.J.Qual.Theory Di ff erential Equations,2012,68:1–18.

[7]Willem M.Minimax Theorems.Boston:Birkh¨auser,1996.

[8]Ahmad S,Lazer A,Paul J.Elementary critical point theory and perturbation of elliptic boundary value problems at resonance.Indiana Univ.Math.J.,1976,25:933–944.

[9]Dr´abek P,Milota J.Methods of Nonlinear Analysis,Applications to Di ff erential Equations. Basel-Boston-Berlin:Birkh¨auser Verlag AG,2007.

[10]Struwe M.Variational Methods:Applications to Nonlinear Partial Di ff erential Equations and Hamiltonian Systems(Fourth Ed.).Berlin-Heidelberg-New York:Springer,2008.

[11]Rabinowitz P.Minimax Methods in Critical Point Theory with Applications to Di ff erential Equations.in:CBMS Region.Conf.Ser.Math.vol.65.Providence,RI:Amer.Math.Soc., 1986.

tion:35A15,35R15,47J30,49S05,58E05,70G75

A

1674-5647(2014)03-0273-11

10.13447/j.1674-5647.2014.03.09

Received date:March 19,2013.

Foundation item:The NSF(10971046 and 11371117)of China,the Shandong Provincial Natural Science Foundation(ZR2013AM009),GIIFSDU(yzc12063)and IIFSDU(2012TS020),and the Project of Shandong Province Higher Educational Science and Technology Program(J09LA55).

E-mail address:keyu 292@163.com(Zhang K Y).