Certain Pair of Derivations on a Triangular Algebra

GUO YING,LI XIA AND MA JING

(School of Mathematics,Jilin University,Changchun,130012)

Certain Pair of Derivations on a Triangular Algebra

GUO YING,LI XIA AND MA JING*

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Du Xian-kun

By using properties of triangular algebra,we prove that if derivations D and G on a triangular algebra T satisfy certain generalized identities,then both D and G are zero mappings.As a corollary we get that if D and G are cocentralizing on T,then both D and G are zero mappings.

triangular algebra,derivation,cocentralizing,the Engel condition

1 Introduction

Let R be a commutative ring with identity,A and B be unital algebras over R,and M be a nonzero(A,B)-bimodule.Then we de fi ne

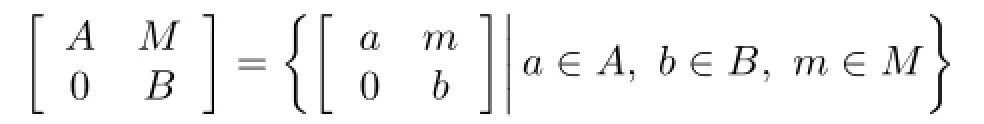
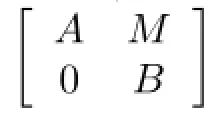
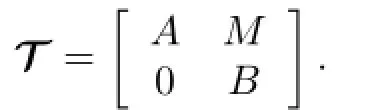
This kind of algebra was fi rst introduced by Chase[1].Harada[2]referred to the triangular algebras as generalized triangular matrix rings.The de fi nition of triangular algebra is somewhat formal and hence they are said to be formal triangular matrix algebras in the case of noncommutative algebras(see[3]).

Throughout this paper,we set[y,x]=[y,x]1=yx−xy;and for k＞1,we set[y,x]k= [[y,x]k−1,x].An R-linear map L∶A→ A is said to satisfy the Engel condition(or to be k-commuting,according to[4])on A if[L(x),x]k=0 for all x∈A.In particular,if [L(x),x]=0 for all x∈A,then L is said to be commuting on A;if[L(x),x]∈Z(A)for all x∈A,then L is said to be centralizing on A,where Z(A)denotes the center of A.

Let R be a ring.A map d∶R→R is called a derivation if

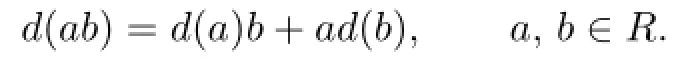
The study of derivations on prime rings was initiated by Posner[5].He proved that if R is a prime ring and d is a nonzero commuting derivation on R,i.e.,d(x)x−xd(x)=0 for all x∈R,then R is commutative.A number of authors have extended this theorem in several ways.Two maps d and g are called cocentralizing on a ring R,if d(x)x−xg(x)∈Z(R)for all x∈R,where Z(R)denotes the center of R.Breˇsar[6]showed that if R is a prime ring, then I is a nonzero left ideal of R;and if derivations d≠0 and g are cocentralizing on I, then R is commutative.Vukman[7]showed that R is commutative if either[D(x),x]2=0 for all x∈R and char(R)≠2 or if[D(x),x]2is central for all x∈R and char(R)≠2,3. Lanski[8]generalized Posner’s theorem by considering a more general case where a derivation satis fi es the Engel condition on a prime ring.

In recent years,some authors also work on derivations on triangular algebras.Xie and Cao[9],Li and Xu[10]gave the exact form of derivations and Jordan derivations on triangular algebras,respectively.Zhang and Yu[11]showed that every Jordan derivation on a triangular algebra is a derivation.Han and Wei[12]declared that(α,β)-derivation,Jordan(α,β)-derivation and Jordan triple(α,β)-derivation are equivalent on triangular algebras.

Du and Wang[4]characterized maps which satisfy the Engel condition on a triangular algebra.

In this paper,we work on derivations on a triangular algebra.We discuss these cases where a pair of derivations of a triangular algebra satisfy certain generalized identities,that is,

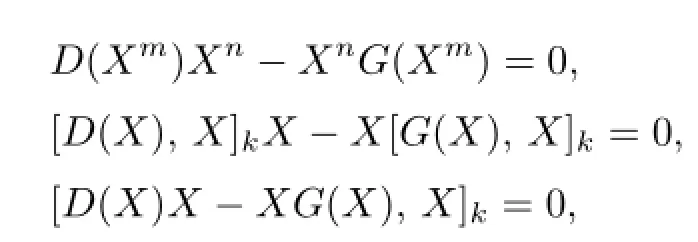
where m,n,k are positive integers.As a corollary we get that if D and G are cocentralizing on a triangular algebra,then D=G=0.

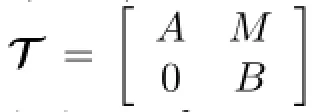
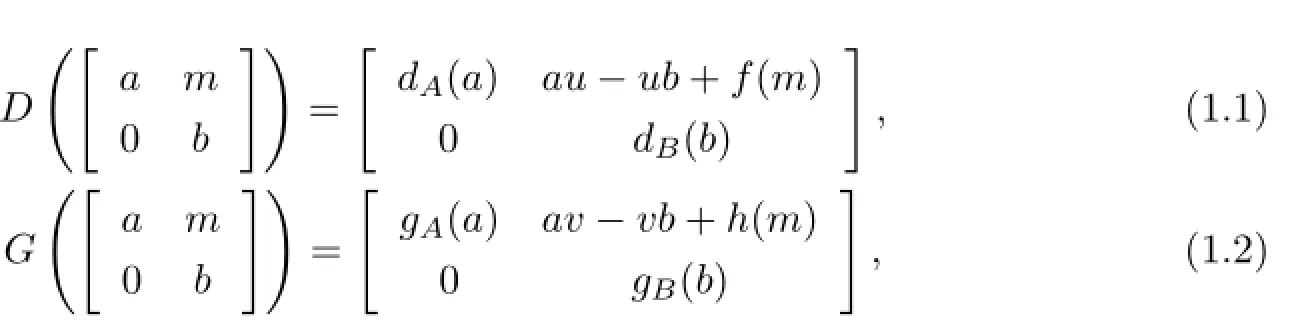
and for all a∈A,b∈B,m∈M,we have

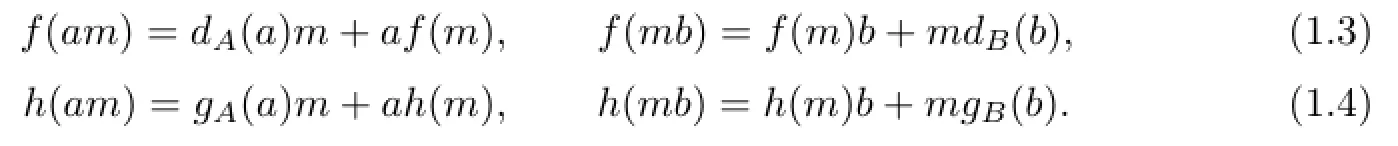
By using the fact that M is faithful as a left A-module and also as a right B-module,we get the following useful lemma easily from(1.3).

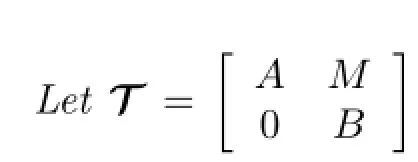
2 A Simple Case:D(X)X−XG(X)=0

Posner[5]proved that if R is a prime ring and d is a nonzero commuting derivation on R, i.e.,d(x)x−xd(x)=0 for all x∈R,then R is commutative.In this section,we prove that if two derivations D and G satisfy the identity D(X)X−XG(X)=0 on a triangular algebra, then D=G=0.

Theorem 2.1LetTbe a triangular algebra andDandGbe derivations onT.IfTsatis fi es the generalized identityD(X)X−XG(X)=0,thenD=G=0.

Proof.Suppose that D and G are of the form(1.1),(1.2),respectively,and T satis fi es the identity D(X)X−XG(X)=0.Then for a∈A,b∈B,x∈M we have

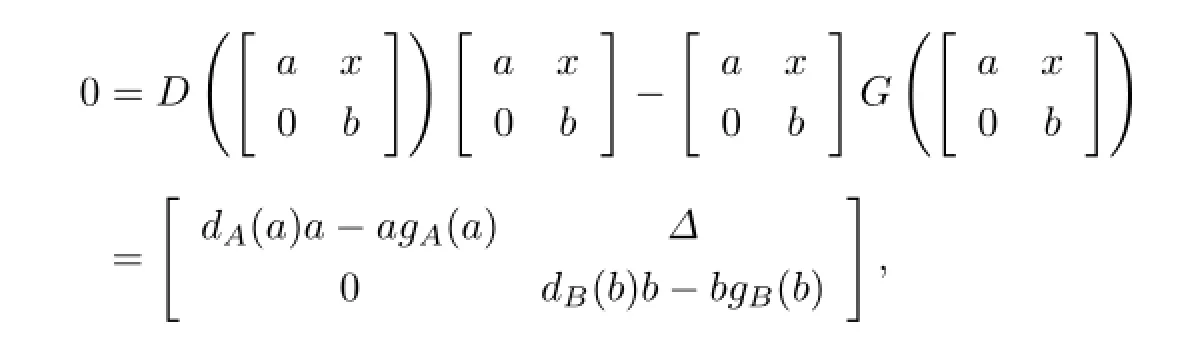
where

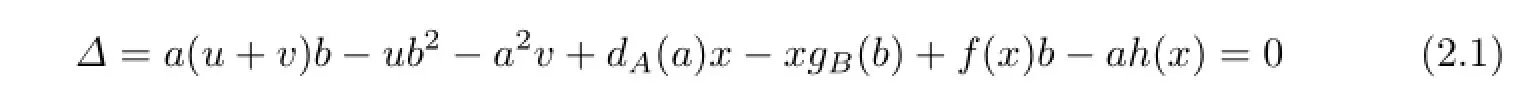
for a∈A,b∈B and x∈M.

Taking a=0,b=1,x=0 in(2.1)gives u=0.Similarly,taking a=1,b=0,x=0 in (2.1)gives v=0.Therefore,(2.1)becomes

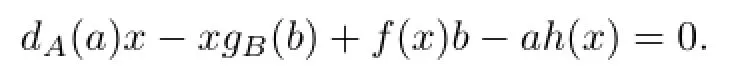
Taking a=0,b=1 gives f(x)=0 for all x∈M.Then we get dA=0 and dB=0 from Lemma 1.1.Hence D=0.Similarly,taking a=1,b=0 gives h(x)=0 for all x∈M. Hence gA=0 and gB=0 and then G=0.

3 Generalizations

In this section,we generalize Theorem 2.1 in di ff erent ways.Firstly,we prove that nonzero derivations D and G do not satisfy the generalized identity D(Xm)Xn−XnG(Xm)=0 on a triangular algebra,where m,n are positive integers.

Theorem 3.1LetTbe a triangular algebra,DandGbe derivations onT,andm,nbe positive integers.ThenTsatis fi es the generalized identityD(Xm)Xn−XnG(Xm)=0if and only ifD=G=0.

Proof.Suppose that D and G are of the form(1.1),(1.2),respectively,and T satis fi es the generalized identity D(Xm)Xn−XnG(Xm)=0.Then for a∈A,b∈B,x∈M we have

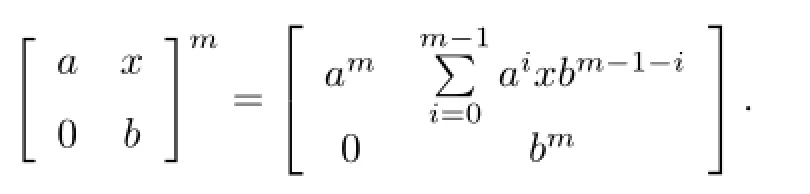
Hence

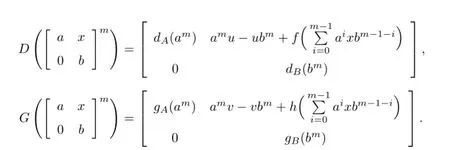
Therefore,direct computation gives

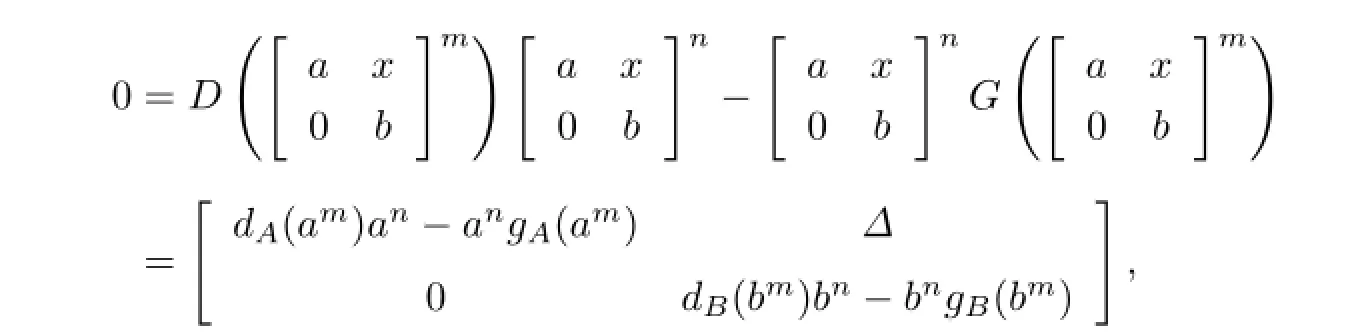
where

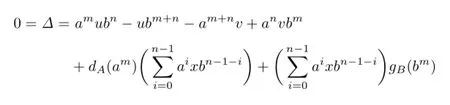
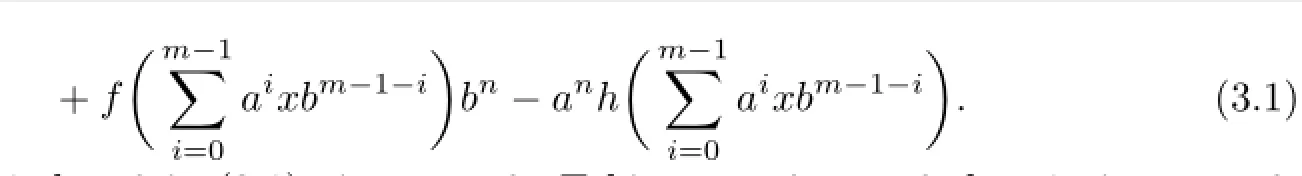
Taking x=0,a=1,b=0 in(3.1)gives v=0.Taking x=0,a=0,b=1 gives u=0. Then(3.1)becomes

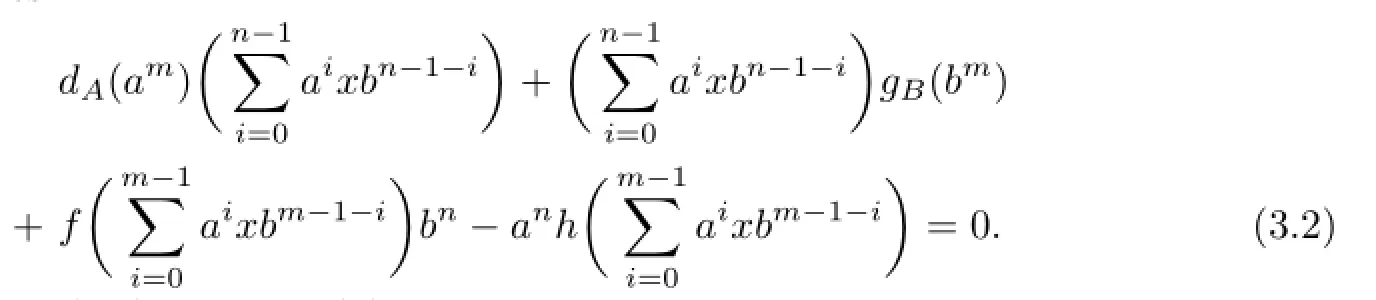
Take a=0,b=1 in(3.2),we get f(x)=0 for all x∈M.Then Lemma 1.1 implies dA=0 and dB=0.Similarly,take a=1,b=0 in(3.2),we get h(x)=0 for all x∈M.Then Lemma 1.1 implies gA=0 and gB=0.Therefore D=G=0.This is the end of the proof.

Now,we generalize Theorem 2.1 through the Engel condition.As a corollary we get that if D and G are cocentralizing on a triangular algebra,then D=G=0.

Direct computation leads to the following lemma which is very useful to the following discussion.

where

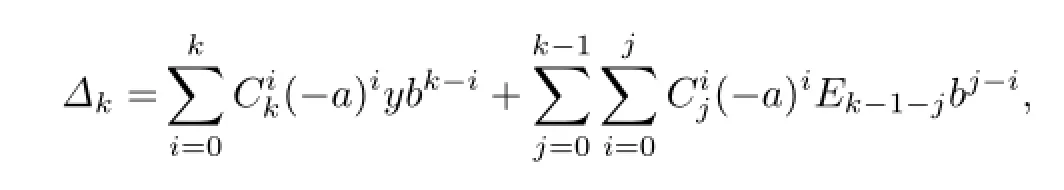
and

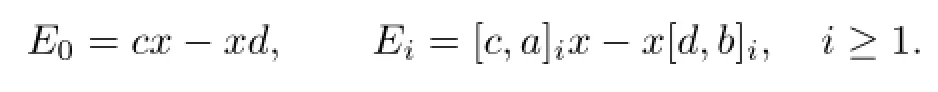
Theorem 3.2LetTbe a triangular algebra,DandGbe derivations onT,andkbe a positive integer.ThenTsatis fi es the generalized identity

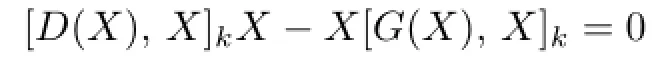
if and only if

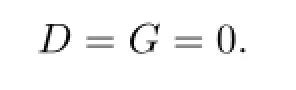
Proof.Suppose that D and G are of the form(1.1),(1.2),respectively,and T satis fi es the generalized identity[D(X),X]kX−X[G(X),X]k=0.By Lemma 3.1,we get

where

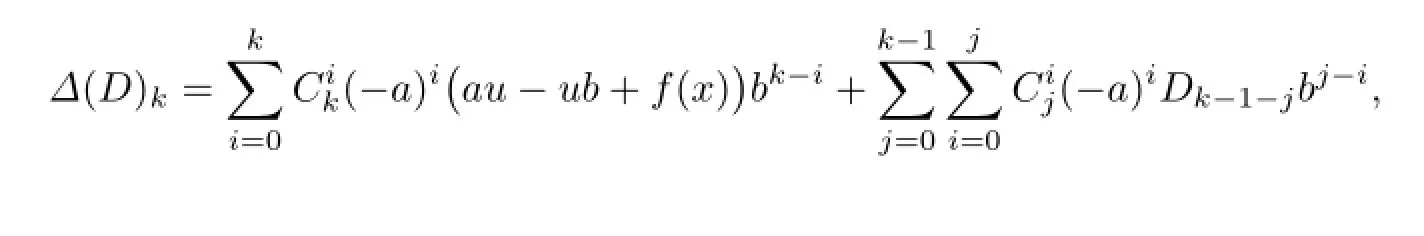
and

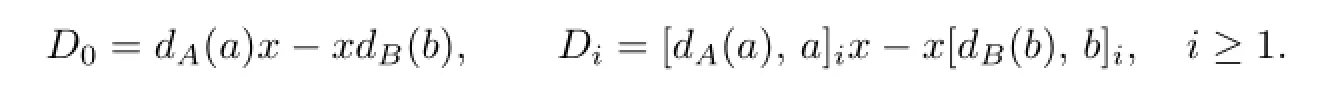
Therefore direct computation gives

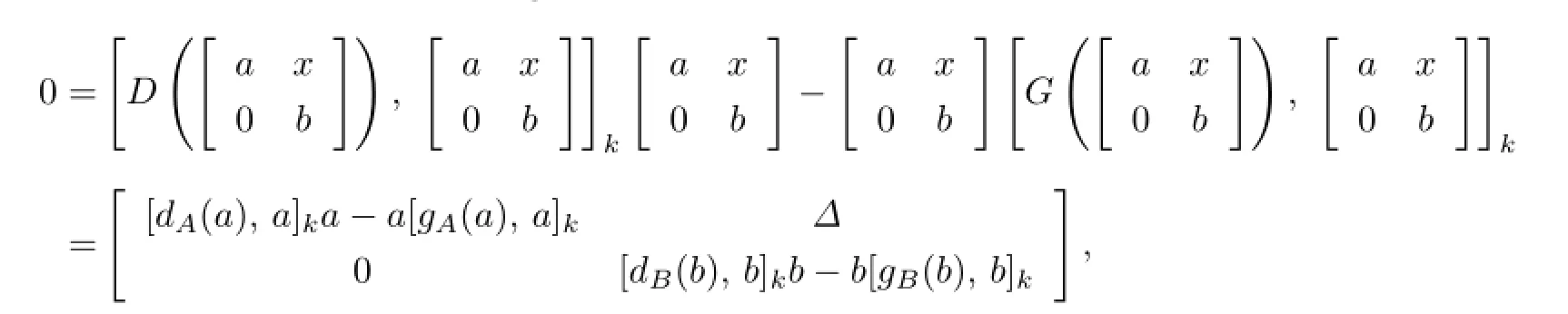
where

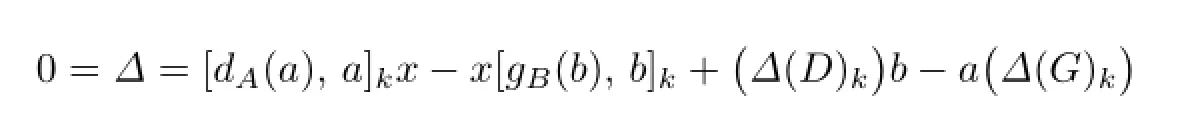
and

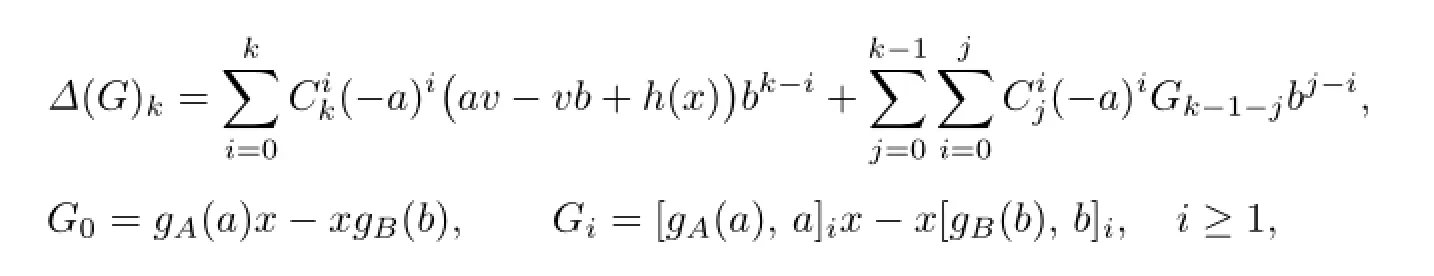
i.e.,

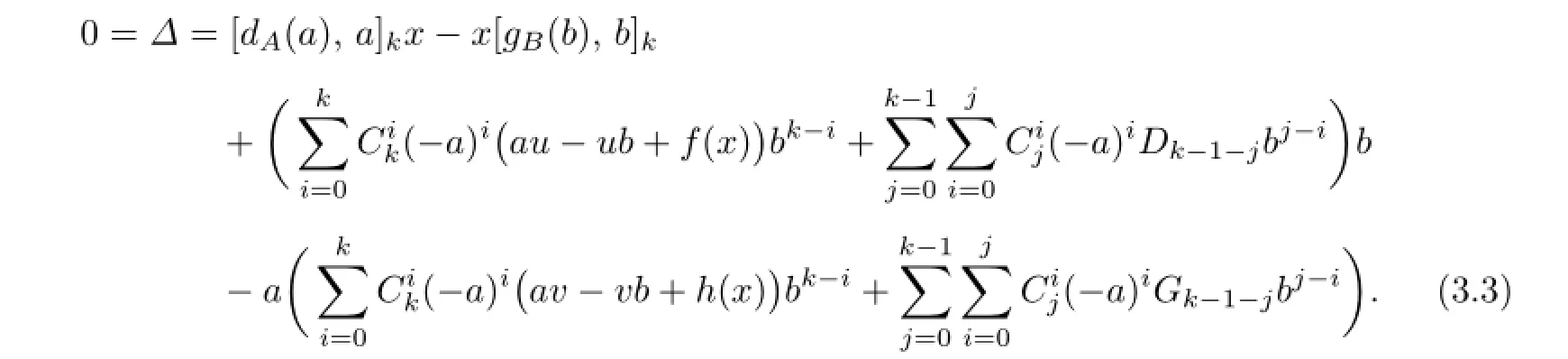
Take a=0,b=1 and x=0 in(3.3),we get u=0.Take a=1,b=0 and x=0 in(3.3), we get v=0.Therefore(3.3)becomes

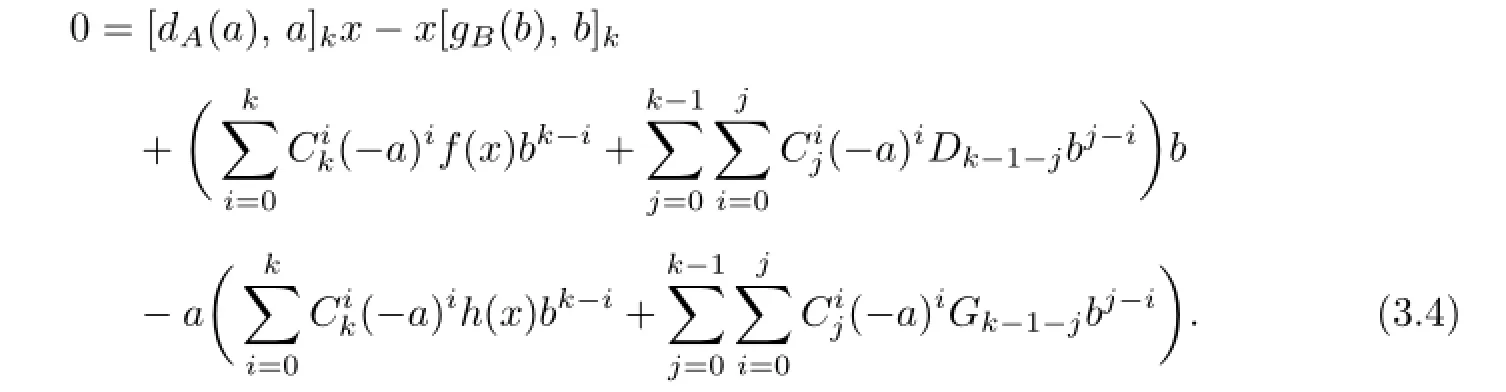
Taking a=0 and b=1 gives

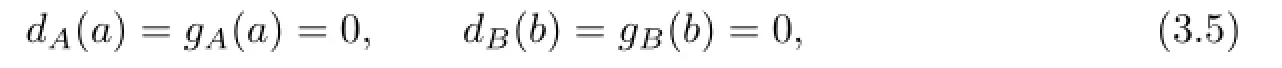
which imply Di=Gi=0.Then(3.4)becomes f(x)=0 for all x∈M,which implies dA=0 and dB=0 by Lemma 1.1.So we get D=0 and(3.4)becomes

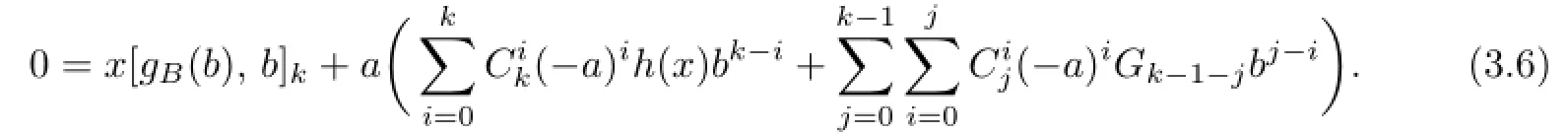
Taking a=1 and b=0 gives gA(a)=0 and gB(b)=0,which imply Gi=0 and(3.6) becomes h(x)=0 for all x∈M.Lemma 1.1 implies gA=0 and gB=0.So we get G=0.

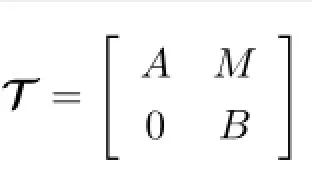
if and only ifD=G=0.

Proof.Suppose that D is of the form(1.1),(1.2),respectively,and T satis fi es the generalized identity[D(X)X−XG(X),X]k=0.Then from Lemma 3.1 we get

where

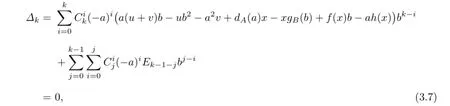
and

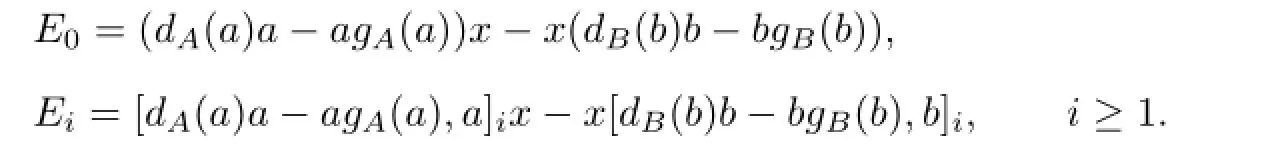
Taking x=0,a=0 and b=1 in(3.7),we get(3.5),which implies Ei=0 for i≥0.So (3.7)gives u=0.Similarly,taking x=0,a=1 and b=0,then we get(3.5)also,which implies Ei=0 for i≥0.So(3.7)gives v=0.Therefore(3.7)becomes

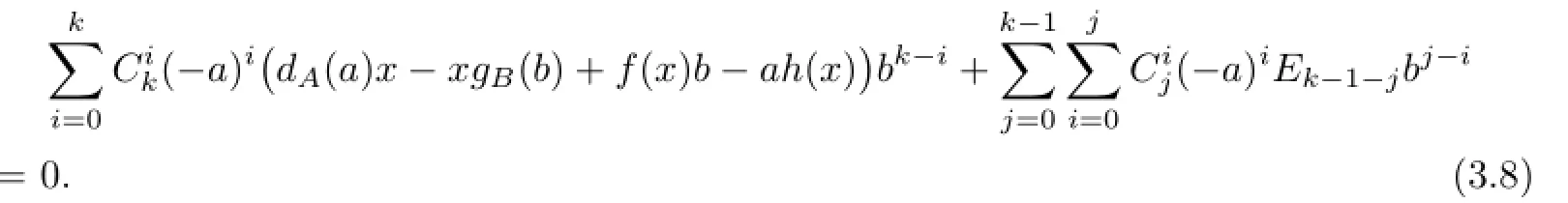
Taking a=0 and b=1 in(3.8),then we get(3.5),furthermore,we get Ei=0 for i≥0. Hence(3.8)gives f=0,which implies dA=0 and dB=0 by Lemma 1.1.Therefore D=0. Similarly,take a=1 and b=0 in(3.8),then gA(a)=0 and gB(b)=0,again we get Ei=0 for i≥0.Hence we get h=0,which implies gA=0 and gB=0 by Lemma 1.1.Therefore

G=0.

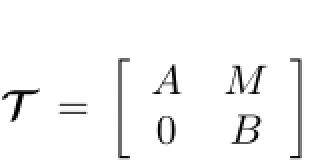
As a corolloary of Theorem 3.3 we see that nonzero derivations are not cocentralizing on a triangular algebra.

Remark 3.1Parallel proofs shows that the theorems here is still true if the plus signs in the generalized identities are replaced by minus signs.

[1]Chase S U.A generalization of the ring of triangular matrices.Nagoya Math.J.,1961,18: 13–25.

[2]Harada M.Hereditary semi-primary rings and triangular matrix rings.Nagoya Math.J.,1966,27:463–484.

[3]Haghany A,Varadarajan K.Study of formal triangular matrix rings.Comm.Algebra,1999,27:5507–5525.

[4]Du Y Q,Wang Y.k-commuting maps on triangular algebras.Linear Algebra Appl.,2012436(5):1367–1375.

[5]Posner E C.Derivations in prime rings.Proc.Amer.Math.Soc.,1957,8:1093–1100.

[6]Breˇsar M.Centralizing mappings and derivations in prime rings.J.Algebra,1993,156:385–394.

[7]Vukman J.Commutating and centralizing mappings in prime rings.Proc.Amer.Math.Soc., 1990,109:47–52.

[8]Lanski C.An Engel condition with derivation.Proc.Amer.Math.Soc.,1993,118(3):731–734.

[9]Xie L P,Cao Y A.Derivations and automorphisms of formal triangular matrix rings.J.Math., 2006,26(2):165–170.

[10]Li J,Xu X W.Derivations and Jordan derivations of Morita context rings(in Chinese).J. Jilin Univ.Sci.,2010,48(5):723–727.

[11]Zhang J H,Yu W Y.Jordan derivations of triangular algebras.Linear Algebra Appl.,2006,419(1):251–255.

[12]Han D,Wei F.Jordan(α,β)-derivations on triangular algebras and related mappings.Linear Algebra Appl.,2011,434(1):259–284.

tion:16W25,15A78,16S50

A

1674-5647(2014)03-0265-08

10.13447/j.1674-5647.2014.03.08

Received date:Nov.19,2013.

Foundation item:The NSF(11101175,11371165)of China,985 Project and 211 Project.

*Corresponding author.

E-mail address:guoy@jlu.edu.cn(Guo Y),jma@jlu.edu.cn(Ma J).