Intrinsic Knotting of Almost Complete Partite Graphs

(School of Science,Beijing Technology and Business University,Beijing,100048)

Intrinsic Knotting of Almost Complete Partite Graphs

LI YANG

(School of Science,Beijing Technology and Business University,Beijing,100048)

Communicated by Lei Feng-chun

LetGbe a completep-partite graph with 2 edges removed,p≥7,which is intrinsically knotted.LetJrepresent any graph obtained fromGby a fi nite sequence of Δ-Yexchanges and/or vertex expansions.In the present paper,we show that the removal of any vertex ofJand all edges incident to that vertex produces an intrinsically linked graph.This result o ff ers more intrinsically knotted graphs which hold for the conjecture presented in Adams’book(Adams C.The Knot Book.New York:W.H.Freeman and Company,1994),that is,the removal of any vertex from an intrinsically knotted graph yields an intrinsically linked graph.

intrinsically knotted graph,Δ-Yexchange,vertex-expansion

1 Introduction

A graph is intrinsically knotted(IK)if every embedding of it in R3contains a non-trivially knotted cycle.Similarly,a graph is intrinsically linked(IL)if every embedding of it in R3contains a pair of non-trivially linked cycles.

Robertsonet al.[1]showed that the intrinsic linking is determined by the seven Petersen graphs.A graph is intrinsically linked if and only if it contains one of the seven as a minor.Since knotless embedding is preserved under edge contraction(see[2]),Robertson and Seymour[3]demonstrated that a similar, fi nite list of graphs exists for the intrinsic knotting property.However,determining such a set of graphs remains difficult.

It is known thatK7andK3,3,1,1along with any graph obtained from these two by Δ-Yexchanges are minor minimal with respect to intrinsic knotting(see[4–7]).Foisy[8]added a new minor minimal graph to the list,moreover,provided a counterexample to the“unsolved question”posed in Adams’book(see[9]):“Whether removing a vertex and all edges incident to that vertex from an intrinsically knotted graph must yield an intrinsically linked graph”. For more counterexamples,please refer to[10].

While Adams’conjecture is not true in general,it does seem to hold for a large class of graphs(see[9]).A graph isk-de fi cient if it is a complete or complete partite graph withk(k=0,1,2,···)edges removed.Campbellet al.[11]have classi fi ed all 0-,1-,2-de fi cient graphs with respect to intrinsic linking and intrinsic knotting,all of which are shown to be hold for Adams’conjecture.It is shown in[12]that any graph obtained from a 0-or 1-de fi cient IK graph by a fi nite sequence of Δ-Yexchanges and/or vertex expansions satis fi es Adams’conjecture.

In this paper,we extend the results in[12]to any graph obtained from completeppartite graphs(p≥7)with 2 edges removed by a fi nite sequence of Δ-Yexchanges and/or vertex expansions,and present a larger array of graphs which hold for Adams’conjecture. In Section 2,we include some necessary de fi nitions and preliminaries.In Section 3,we state the main theorems and give their proofs.

2 Preliminaries

Throughout the paper we take an embedded graph to mean a graph embedded in 3-space, where all the embeddings are tame.In this section,we present some useful lemmas and notations which are used throughout the paper.

Kndenotes the complete graph onnvertices,andKn1,n2,···,npdenotes the completep-partite graph,p≥2,withnivertices in thei-th part.Kn1,n2,···,np−k,p≥1,k≥0, denotes the graph obtained by removingkedges fromKn1,n2,···,np.Note here that deleting any Δ from a graph mentioned throughout the paper means deleting the edges of Δ from the graph.And for the special case that graphGcontains no triangle,we assumeG−Δ≡G.

Recall that a vertex expansion of a vertexvin a graphGis achieved by replacingvwith two verticesv′andv′′,adding the edge(v′,v′′),and connecting a subset of the edges that are incident withvtov′,and connecting the remaining edges that are incident withvtov′′.The reverse of this operation is edge contraction.

LetGbe a graph which contains a triangle Δ.Remove the three edges of Δ fromG. Add three new edges,connecting the three vertices of Δ to a new vertex.The resulting graphG′is said to be obtained fromGby a Δ-Ymove.

A minor of a graphGis the graph resulting from a fi nite number of vertex deletions, edge deletions and edge contractions onG.If we know that a graphGcontains a linked (knotted)minor,thenGmust also be linked(knotted).Conversely,if we can realizeGas a minor of an unlinked(unknotted)graph,thenGmust also be unlinked(unknotted).

Lemma 2.1[11]Kn1+n2,n3,···,npis a minor of Kn1,n2,n3,···,np,where p≥3.Similarly,Kn1+n2,n3,···,np−k edges is a minor of Kn1,n2,n3,···,np−k edges,where p≥3.

Lemma 2.2[12]Let G be an IK0-de fi cient graph listed in Table2.1.Then the removal of any triangle of G yields an IL graph.

Remark 2.1 As indicated in[11],in the following the tables and the proof presented, given a complete partite graph,we refer to parts alphabetically with capital letters and the vertices of those parts by lower case letters.Denote by“−e”the removal of any edge from a particular graph.For example,inK5,6,the part with 5 vertices is called partAand the part with 6 vertices is called partB.An edge between partsAandBis labeled(a,b).Please refer to[11]for the detailed descriptions of the notations.

Lemma 2.3[12]Let G be an IK1-de fi cient graph listed in Table2.2.Then the removal of any triangle of G yields an IL graph.

Table 2.2 Intrinsic knotting of 1-de fi cient graphs

For the reader’s convenience,we demonstrate the classi fi cation of 0-,1-,2-de fi cient graphs with respect to intrinsic linking and knotting in the following.

Lemma 2.4[11]The0-,1-,2-de fi cient graphs are classi fi ed with respect to intrinsic linking according to Tables2.3–2.5,respectively.

Table 2.3 Intrinsic linking of complete and completek-partite graphs

Table 2.4 Intrinsic linking of 1-de fi cient graphs

Table 2.5 Intrinsic linking of 2-de fi cient graphs

(continued)

Lemma 2.5[11,13]The0-,1-de fi cient graphs are classi fi ed with respect to intrinsic knotting according to Tables2.1and2.2,respectively.

3 Main Theorems

In this section,we give two main theorems,and prove Adams’conjecture for almost complete partite graphs satisfying certain conditions.

Theorem 3.1Let G be K2,1,1,1,1,1,1−{(a1,b),(a1,c)},K2,1,1,1,1,1,1−{(a1,b),(a2,b)}, K2,1,1,1,1,1,1−{(a1,b),(c,d)},K2,1,1,1,1,1,1−{(b,c),(c,d)},K3,1,1,1,1,1,1−2e or K2,2,1,1,1,1,1−2e,which is intrinsically knotted,let J represent any graph obtained from G by a fi nite sequence ofΔ-Y exchanges and/or vertex expansions,where“−2e”denotes the removal of any two edges from a graph.Then the removal of any vertex of J,and all edges incident to that vertex,yields an intrinsically linked graph.

Proof.The former part of the proof depends heavily on some of Foisy’arguments.We make slight changes on it for the reader’s convenience.

LetGnbe obtained fromGby a sequence ofn(＞0)Δ-Ymoves and/or vertex expansions. Suppose that the claim is true forGn.Now we assume thatGn+1is obtained by a vertex expansion onGn,andvis a vertex ofGn+1.If the vertex expansion onGndoes not createv,thenGn+1−vis the graph obtained fromGn−vby a vertex expansion.Since vertex expansion preserves the property of intrinsic linking(see[7]),it follows from the assumptionthatGn−vis IL thatGn+1−vis IL.Ifvis created by the vertex expansion onGnandwis the vertex ofGnwhich are split to obtainGn+1,Gn+1−vcontainsGn−was a subgraph. The claim thatGn−wis IL implies thatGn+1−vis IL.

Next we do a Δ-Ymove onGn.Letvbe a vertex ofGn+1.On the one hand,if the Δ-Yused fromGntoGn+1does not createvandvis not a vertex of Δ exchanged,thenGn+1−vis the graph obtained fromGn−vvia a Δ-Yexchange.By assumption thatGn−vis IL,soGn+1−vis IL.On the other hand,ifvis a vertex of the Δ inGnwhich is swapped for aYto createGn+1,thenGn+1−vis homeomorphic toGn−v,and soGn+1−vis IL. Finally,suppose thatvis the vertex made by the Δ-Ymove.Letxv,yv,zvrepresent three edges which make up theY.ThenGn+1−visGnwith the Δ removed.So our proof will fi nish once we have shown thatGnwith any Δ removed is IL.Since Δ-Ymoves and vertex expansions(of graphs without multiple edges)do not produce any cycle of length three,any cycle of length three inGnmust have been presented inG.The proof for the theorem is thus reduced to show thatGwith any Δ removed is IL.The remaining work in the proof is to check whetherG−Δ is IL.We assumeG−Δ=H.

We proceed to check the ILness of the minor or subgraph ofHwhen we prove the ILness of a given graph.The readers can easily check the tables as listed in Section 2.

H=K2,1,1,1,1,1,1−{(a1,b),(a1,c)}−Δ has 7 cases as shown in Fig.3.1.

Fig.3.1

In Fig.3.1(1)–(3)and(5)–(7),by deleting the vertexa1one can fi nd thatHhasK1,1,1,1,1,1,1−Δ as a minor.By Lemma 2.2,K1,1,1,1,1,1,1−Δ is IL.In Fig.3.1(4),HcontainsK2,1,1,1,1,1,1−a1−(d,e)=K1,1,1,1,1,1,1−(d,e)as a minor.Check Table 2.4 and we can get thatK2,1,1,1,1,1,1−{(a1,b),(a1,c)}−Δ is IL.

H=K2,1,1,1,1,1,1−{(a1,b),(a2,b)}−Δ has 3 cases as shown in Fig.3.2.

Fig.3.2

In Fig.3.2(1),Hcontains a subgraphK2,1,1,1,1,1,1−a1−(a2,b)−(c,d)of the formK1,1,1,1,1,1,1−2eas a minor.In Fig.3.2(2),delete the vertexb,then combining partsCandDshows thatHhas a subgraphK2,2,1,1,1a minor by Lemma 2.1.In Fig.3.2(3),bycombining partsAandBone can fi nd thatHhasK3,1,1,1,1,1−Δ as a minor by Lemma 2.1.By Lemma 2.2,K3,1,1,1,1,1−Δ is IL.By checking Tables 2.3 and 2.5 one can get thatK2,1,1,1,1,1,1−{(a1,b),(a2,b)}−Δ is IL.

H=K2,1,1,1,1,1,1−{(a1,b),(c,d)}−Δ has 9 cases as shown in Fig.3.3.

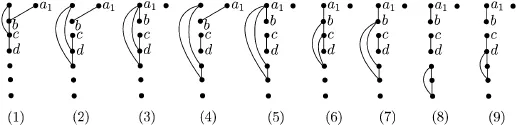
Fig.3.3

In Fig.3.3(1)and(2),after deleting the vertexc,by combining some parts one can fi nd thatHhasK3,3,1as a minor by Lemma 2.1.In Fig.3.3(3)–(5)and(7),after removing the vertexa1,by combining some parts we can get thatHcontains a subgraphK3,3,1as a minor by Lemma 2.1.In Fig.3.3(6),delete the vertexb,then combining PartsC,DandEgives thatHhasK3,2,1,1as a minor by Lemma 2.1.In Fig.3.3(8),by combining partsAandB, combining partsCandD,combining partsE,FandGone can obtain thatHcontains a subgraphK3,3,2as a minor by Lemma 2.1.In Fig.3.3(9),by combining partsAandB,and combining partsC,D,EandFwe can fi nd thatHhasK4,3,1as a minor by Lemma 2.1. Checking Table 2.3 shows thatK2,1,1,1,1,1,1−{(a1,b),(c,d)}−Δ is IL.

H=K2,1,1,1,1,1,1−{(b,c),(c,d)}−Δ has 6 cases as shown in Fig.3.4.

Fig.3.4

In Fig.3.4(1)and(3),after deleting the vertexd,by combining some parts one can get thatHhasK3,2,1,1as a minor by Lemma 2.1.In Fig.3.4(2),by combining partsA,EandF,combining partsB,CandDwe can show thatHcontainsK4,3,1as a minor by Lemma 2.1.In Fig.3.4(4)and(5),remove the vertexc,then combining some parts gives thatHhasK3,3,1as a minor by Lemma 2.1.In Fig.3.4(6),by combining partsB,CandD,combining partsE,FandGone can show thatHcontainsK3,3,2as a minor by Lemma 2.1.So,by checking Table 2.3 we can conclude thatK2,1,1,1,1,1,1−{(b,c),(c,d)}−Δ is IL.

H=K3,1,1,1,1,1,1−2e−Δ.There are 2 cases when considering the ways we delete the Δ.For the caseK3,1,1,1,1,1,1−{(a,b),(b,c),(c,a)},by combing partsA,BandC,one can get thatHhasK5,1,1,1,1−e(orK5,1,1,1,1−2e)as a minor by Lemma 2.1.For the caseK3,1,1,1,1,1,1−{(b,c),(c,d),(d,b)},combing partsB,CandDgives thatHhasK3,3,1,1,1−e(orK3,3,1,1,1−2e)as a minor by Lemma 2.1.Finally,checking Tables 2.4 and 2.5 shows thatK3,1,1,1,1,1,1−2e−Δ is IL.

H=K2,2,1,1,1,1,1−2e−Δ.Considering the ways we delete the Δ gives 3 cases.For the caseK2,2,1,1,1,1,1−{(a,b),(b,c),(c,a)},by combining partsA,BandC,one can get thatHhasK5,1,1,1,1−e(orK5,1,1,1,1−2e)as a minor by Lemma 2.1.For the caseK2,2,1,1,1,1,1−{(a,c),(c,d),(d,a)},combining partsA,CandDshows thatHhasK4,2,1,1,1−e(orK4,2,1,1,1−2e)as a minor by Lemma 2.1.For the caseK2,2,1,1,1,1,1−{(c,d),(d,e),(e,c)}, by combing partsC,DandE,one can get thatHhasK3,2,2,1,1−e(orK3,2,2,1,1−2e)as a minor by Lemma 2.1.Checking Tables 2.4 and 2.5 shows thatK2,2,1,1,1,1,1−2e−Δ is IL.

Lemma 3.1If for any two edges2e and triangleΔnot containing2e of Kn1,n2,···,npthe graph Kn1,n2,···,np−2e−Δis intrinsically linked,then for any two edges2e and triangleΔnot containing2e of Kn1,n2,···,ni+1,···,npthe graph Kn1,n2,···,ni+1,···,np−2e−Δis also intrinsically linked.

Proof.The casep=1 is obvious.Whenp=2,considerv,the vertex which was added toKn1,n2.SinceKn1,n2contains no triangle,we check whetherKn1+1,n2−2eandKn1,n2+1−2eare intrinsically linked.There are three subcases to discuss:(i)If the two edges 2edeleted fromKn1+1,n2andKn1,n2+1are not incident to the vertexv,thenKn1,n2−2e−Δ is a subgraph ofKn1+1,n2−2e−Δ andKn1,n2+1−2e−Δ.(ii)If one of the two edges 2edeleted fromKn1+1,n2andKn1,n2+1is incident to the vertexv,removingvthen results inKn1,n2−e−Δ.It follows directly from the given condition thatKn1,n2−2e−Δ is IL thatKn1+1,n2−2e−Δ andKn1,n2+1−2e−Δ are IL.(iii)If the two edges 2edeleted fromKn1+1,n2andKn1,n2+1are incident to the vertexv,removingvresults inKn1,n2−Δ.It is clear thatKn1,n2−2e−Δ is a subgraph ofKn1+1,n2−2e−Δ andKn1,n2+1−2e−Δ, which imply thatKn1+1,n2−2e−Δ andKn1,n2+1−2e−Δ are IL.

Whenp≥3,if the two edges 2edeleted fromKn1,n2,···,ni+1,···,npare not incident to the vertexvand the deleted Δ does not containv,then it is obvious thatKn1,n2,···,ni+1,···,np−2e−Δ is IL.Whenp≥3 and the case that the deleted Δ containsv,the vertex added toKn1,n2,···,ni+1,···,np,removingvand Δ fromKn1,n2,···,ni+1,···,npresults in a 1-de fi cient graph,say,Kn1,n2,···,,np−e1.According to the given condition that the deleted Δ does not contain 2e,e1is di ff erent from the two edges 2edeleted fromKn1,n2,···,ni+1,···,np.There are three subcases to consider:(i)If the deleted 2eare not incident to the vertexv,then by the given condition we can fi nd a Δ1which containse1but not 2einKn1,n2,···,np.According to the given condition,Kn1,n2,···,np−2e−Δ1is IL.SinceKn1,n2,···,ni+1,···,np−2e−Δ containsKn1,n2,···,np−2e−Δ1as a subgraph,we know thatKn1,n2,···,ni+1,···,np−2e−Δ is IL.(ii)Denote bye′ande′′any two edges deleted fromKn1,n2,···,ni+1,···,np.If one of any two edges deleted fromKn1,n2,···,ni+1,···,npis incident to the vertexv,saye′,then removing the vertexvresults in a 2-de fi cient graphKn1,n2,···,np−e1−e′′.By the assumption thatKn1,n2,···,np−e1−e′′−Δ2is IL,Kn1,n2,···,np−e1−e′′is IL,where Δ2is any triangle inKn1,n2,···,np−e1−e′′.This together with the fact thatKn1,n2,···,ni+1,···,np−e′−e′′−Δ containsKn1,n2,···,np−e1−e′′as a subgraph imply thatKn1,n2,···,ni+1,···,np−e′−e′′−Δ isIL.(iii)If any two edges deleted fromKn1,n2,···,ni+1,···,npare incident to the vertexv,thenKn1,n2,···,ni+1,···,np−2e−Δ containsKn1,n2,···,np−e1as a subgraph.It follows from the assumption thatKn1,n2,···,np−e1is IL thatKn1,n2,···,ni+1,···,np−2e−Δ is IL.

Lemma 3.2If for any two edges2e and triangleΔnot containing2e of Kn1,n2,···,npthe graph Kn1,n2,···,np−2e−Δis intrinsically linked,then for any two edges2e and triangleΔnot containing2e of Kn1,n2,···,np,1the graph Kn1,n2,···,np,1−2e−△is also intrinsically linked.

Proof.By using a similar proof to the one in Lemma 3.1,we can prove the casesp=1 andp≥3.Whenp=2,we prove the ILness ofK5,4,1−2esince it can be seen from Table 2.5 that all of the other IL 2-de fi cient graphKn1,n2−2econtainsK5,4−2eas a subgraph.

H=K5,4,1−2e−Δ has 21 cases as shown in Fig.3.5.

Fig.3.5

In Fig.3.5(1),(3)–(6),(8)–(10)and(16)–(19),Hcontains a subgraphK5,4,1−Δ−e1−a=K4,4,1−e1−Δ,by Lemma 2.3,which is IL.In Fig.3.5(2),(7),(11)and(21),Hcontains a subgraphK5,4,1−Δ−a=K4,4,1−Δ,which is IL by Lemma 2.2.In Fig.3.5(12),Hcontains a subgraphK5,4,1−a−e3=K4,4,1−e3.In Fig.3.5(13),Hcontains a subgraphK5,4,1−b−e3=K5,3,1−e3.In Fig.3.5(14)and(15),Hcontains a subgraphK5,4,1−c−e3=K5,4−e3.In Fig.3.5(20),Hcontains a subgraphK5,4,1−a−e2−e3=K4,4,1−e2−e3. By checking Tables 2.4 and 2.5 one can get thatK5,4,1−2e−Δ is IL.It follows thatKn1,n2,1−2e−Δ is IL.

Theorem 3.2Let G be a complete p-partite graph Kn1,n2,···,npwith2edges removed, p≥8,which is intrinsically knotted,let J represent any graph obtained from G by a fi nite sequence ofΔ-Y exchanges and/or vertex expansions.Then the removal of any vertex of J, and all edges incident to that vertex,yields an intrinsically linked graph.

Proof.The former part of the proof is similar to the one in Theorem 3.1.By Lemmas 3.1 and 3.2,we only need to check the ILness ofK1,1,1,1,1,1,1,1−2e−Δ=K8−2e−Δ.

If any two edges deleted fromK8are not incident to a vertex of Δ,there are two subcases:K8−Δ−{(a,b),(a,c)}andK8−Δ−{(a,b),(c,d)}.In the caseK8−Δ−{(a,b),(a,c)}, delete the vertexato getK7−Δ.In the caseK8−Δ−{(a,b),(c,d)},contract the edge (a,c)toK7−Δ.It is shown in[8]thatK7−Δ is IL.If one of the two deleted edges inK8is incident to the vertexaof Δ,there are two subcases:K8−Δ−{(a,b),(c,d)}andK8−Δ−{(a,b),(b,c)}.In either case,delete the vertexato getK7−2e.If the two edges deleted are incident to a vertex of Δ,there are three subcases,one of which is that the two edges share the vertex from Δ but the other endpoints are two di ff erent vertex not in Δ. The other subcases is that the two edges are incident to two di ff erent vertex of Δ while they share no vertex which is not in Δ.The third subcase is that the two edges are incident to two di ff erent vertex of Δ but they have common endpoints which is not in Δ.In either case, remove a vertex to getK7−eorK7−2e.By checking Tables 2.4 and 2.5,one can get thatK8−2e−Δ is IL.

[1]Robertson N,Seymour P,Thomas R.Sachs’linkless embedding conjecture.J.Combin.Theory Ser.B,1995,64(2):185–227.

[2]Neˇsetˇril J,Thomas R.A note on spatial representations of graphs.Comment.Math.Univ. Carolin.,1985,26:655–659.

[3]Robertson N,Seymour P.Graph minors XX.Wagner’s Conjecture.J.Combin.Theory Ser. B,2004,92(2):325–357.

[4]Conway J,Gordon C.Knots and links in spatial graphs.J.Graph Theory,1983,7(4):445–453.

[5]Foisy J.Intrinsically knotted graphs.J.Graph Theory,2002,39(3):178–187.

[6]Kohara T,Suzuki S.Some Remarks on Knots and Links in Spatial Graphs.in:Kawauchi A. Knots 90:Proceedings of the International Conference on Knot Theory and Related Topics Held in Osaka(Japan),August 15-19,1990.Berlin:Walter de Gruyter,1992:435–445.

[7]Motwani R,Raghunathan A,Saran H.Constructive Results from Graph Minors:Linkless embeddings.29th Annual Symposium on Foundations of Computer Science,IEEE,1988,398–409.

[8]Foisy J.A newly recognized intrinsically knotted graph.J.Graph Theory,2003,43(3):199–209.

[9]Adams C.The Knot Book.New York:W.H.Freeman and Company,1994.

[10]Foisy J.More intrinsically knotted graphs.J.Graph Theory,2007,43(2):115–124.

[11]Campbell J,Mattman T,Ottman R,Pyzer J,Rodrigues M,Williams S.Intrinsic knotting and linking of almost complete graphs.Kobe J.Math.,2008,25(1/2):39–58.

[12]Li Y,Qin J H,Lei F C,Wang X K,Zhang X H.Triangle-Yexchanges on intrinsic knotting of almost complete and complete partite graphs.J.Knot Theory Rami fi cations,2012,21(4). DOI:10.1142/S021821651100990X.

[13]Blain P,Bowlin G,Fleming T,Foisy J,Hendricks J,Lacombe J.Some results on intrinsically knotted graphs.J.Knot Theory Rami fi cations,2007,16(6):749–760.

tion:57M25,57M27

A

1674-5647(2014)02-0183-10

10.13447/j.1674-5647.2014.02.09

Received date:Jan.6,2014.

Foundation item:The Scienti fi c Research Common Program(KM201410011006)of Beijing Municipal Commission of Education,the Research Foundation(QNJJ2012-26)for Youth Scholars of Beijing Technology and Business University,the NSF(1122013,1132002)of Beijing and the Importation and Development of High-caliber Talents Project(CIT&TCD201304029)of Beijing Municipal Institutions.

E-mail address:lyanghit@163.com(Li Y).