The Closed Subsemigroups of a Cli ff ord Semigroup

(College of Mathematics and Information Science,Jiangxi Normal University, Nanchang,330022)

The Closed Subsemigroups of a Cli ff ord Semigroup

FU YIN-YIN AND ZHAO XIAN-ZHONG

(College of Mathematics and Information Science,Jiangxi Normal University, Nanchang,330022)

Communicated by Du Xian-kun

semilattice,closed subsemigroup,Cli ff ord semigroup

1 Introduction

By a semiring we mean a type〈2,2〉algebra(S,+,·)satisfying the following identities:

(SR1)x+(y+z)≈(x+y)+z;

(SR2)x(yz)≈(xy)z;

(SR3)x(y+z)≈xy+xz,(x+y)z=xz+yz.

The power semiring of a semigroupSand the closed subsemigroups ofSare introduced and studied by Zhao[1].By studying of the power semiring of an idempotent semigroupSand the closed subsemigroups of an idempotent semigroupS,in[2–3],Pastijnet al.obtained the lattice of all subvarieties of the variety consisting of the semiringsSfor which(S,+)is a semilattice and(S,·)is an idempotent semigroup(the concepts of lattices and varietiesare introduced in[4]).This lattice is distributive and contains 78 varieties precisely.Each of those is fi nitely based and generated by a fi nite number of fi nite ordered bands.

LetSbe a semigroup andP(S)the set of all nonempty subsets ofS.ForA,B∈P(S), we de fi ne

Then(P(S),∪,◦)becomes a semiring,which is called the power semiring ofS.A subsemigroupCof a semigroupSis said to be closed(see[1])if

holds for alla,b∈S,s,t∈S1.The set of all closed subsemigroups ofSis denoted byP(S).

LetSbe a semigroup andAa nonempty subset ofS.denotes the closed subsemigroup ofSgenerated byA,i.e.,the smallest closed subsemigroup ofScontainingA.De fi ne inductively(see[1])setsA(i)(i≥1)as follows:A(1)is the subsemigroup ofSgenerated byA;for anyi≥1,A(i+1)is the subsemigroup ofSgenerated by the set

LetSbe a semigroup andthe set of all closed subsemigroups ofS.ThenP(S) becomes a semiring equipped with the addition and the multiplication as follows:

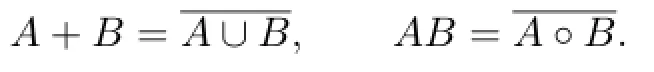
Also,it is easy to see that the mapping

is a semiring homomorphism.The kernel ofτwas written asρin[1].That is to say,

2 Closed Subsemigroup

Theorem 2.1Let G be a group and1the identity element of G.Then

Proof.We fi rst prove that=G.It is obvious that{1}⊆G.Also,since 1=1aa−1for anya∈G,we havea=1aaa−1by the de fi nition of closed subsemigroups.

That is to say,.So it follows that=G.

In the following we prove that=Gfor everyA∈P(G).Since 1∈A◦G,we haveThus it follows thatTherefore

Since

we have immediately that

This completes the proof.

By Theorem 2.1,immediately,we have

Corollary 2.1Let G be a group.Then ρ=∇,where∇denotes the universal relation on G.

By the de fi nition of closed subsemigroups,it is easy to see that every subsemilattice of a semilattice is closed.Thus we have immediately

Theorem 2.2Let Y be a semilattice and Y′a nonempty subset of Y.Then

where〈Y′〉denotes the subsemilattice of Y generated by Y′.

Lemma 2.1Let S=[Y;Gα;ϕα,β]be a Cli ff ord semigroup.Then

Proof.Denote bya−1the inverse ofainGα,and denote by 1αthe identity element ofGα,whereα∈Yanda∈Gα.Sincea=aa−1for anya∈Gα,we have 1α=aa−1a−1a∈{a}by the de fi nition of closed subsemigroups.Givenb∈Gα,since 1α=b−1b1α∈we haveb=b−1bb1α∈This implies thatGα⊆On the other hand,it is clear thatGαis a semigroup ofScontaininga.In the following we prove thatGαis closed.Suppose thatsat,sbt∈Gαfor somea,b∈S,s,t∈S1.Consider the following cases:

(1)Ifs=1 andt=1,it is easy to see thatsabt=ab∈Gα;

(2)Ifs≠1 andt=1,then there existµ,ν,γ∈Ysuch thata∈Gµ,b∈Gν,s∈Gγ. Thus we have

and

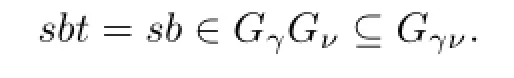
It follows immediately thatα=γµ=γνsincesat,sbt∈Gα.Hence,we can show thatα=γµν,and so

(3)Ifs=1 andt≠1,then we can similarly prove thatsabt=abt∈Gα;

(4)Ifs≠1 andt≠1,i.e.,s,t∈S,then there existµ,ν,γ,δ∈Ysuch thata∈Gµ,b∈Gν,s∈Gγ,t∈Gδ.Thus we have

and

It follows immediately thatα=γµδ=γνδsincesat,sbt∈Gα.Hence,we can show thatα=γµνδ,and so

Lemma 2.2Let S=[Y;Gα;ϕα,β]be a Cli ff ord semigroup and A a nonempty subset of S.Then

where

as required.

Lemma 2.3Let S=[Y;Gα;ϕα,β]be a Cli ff ord semigroup and Y′a nonempty subset of Y.Then

whereY′denotes the closed subsemigroup of Y generated by Y′.

Consider the following cases:

(1)Ifs=1 andt=1,then it is easy to see that

(2)Ifs≠1 andt=1,then there existα,β,γ∈Ysuch thata∈Gα,b∈Gβ,s∈Gγ. Thus we have

and

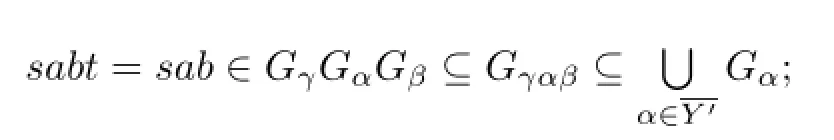
(3)Ifs=1 andt≠1,then we can similarly prove that

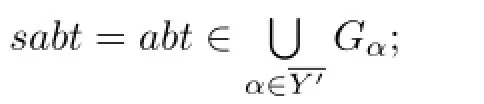
(4)Ifs≠1 andt≠1,i.e.,s,t∈S,then there existα,β,γ,δ∈Ysuch thata∈Gα,b∈Gβ,s∈Gγ,t∈Gδ.Thus we have

and

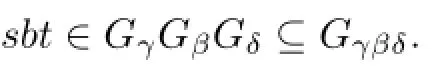
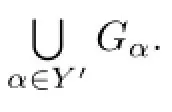
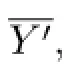
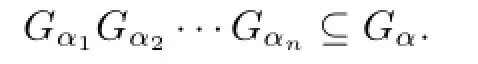
This implies thatGα∩A≠∅.Givena∈Gα∩A,we have

by Lemma 2.1,and so

as required.

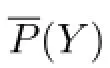
Theorem 2.3Let S=[Y;Gα;ϕα,β]be a Cli ff ord semigroup and A a nonempty subset of S.Then

That is to say,

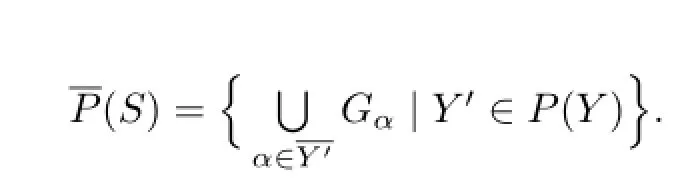
We showed by Theorem 2.2 thatis the set of all subsemilattices of a semilatticeY.Also it is shown by Theorem 2.3 that

for a Cli ff ord semigroupS=[Y;Gα;ϕα,β].Furthermore,we prove that the semiringP(S)is isomorphic to the semiringfor a Cli ff ord semigroupS=[Y;Gα;ϕα,β].The following Lemma 2.4 is needed.

Proof.Let

and

Then we need to prove thatDis a subsemilattice ofYgenerated byI.

It is obvious thatI⊆D.Also,it is easy to verify thatDis a subsemilattice ofY.In fact,for anyα,β∈D,one has

Thenαβ∈D,and we have

Suppose thatCis a subsemilattice ofYcontainingI.To proveD⊆C,we only need to prove by induction that

since

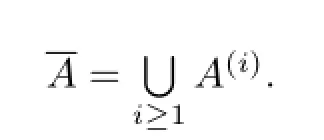
First,consider the casei=1.For any

one has

Assume thata=a1a2···as,wheream∈A(1≤m≤s).SinceA∈P(S),there existu1,u2,···,us∈Ysuch that

It follows immediately thatum∈I(1≤m≤s),and sou1u2···us∈C.Since

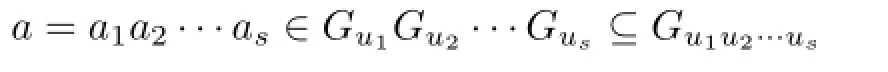
anda∈Gα,we getα=u1u2···us∈C.This shows that

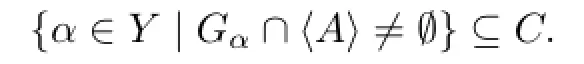
Next,assume that

We prove that

For anyα∈{α∈Y|Gα∩A(i+1)≠∅},we have

Then

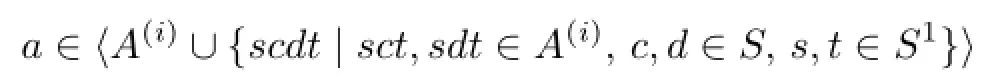
by the de fi nition of the setA(i+1)in[1].Let

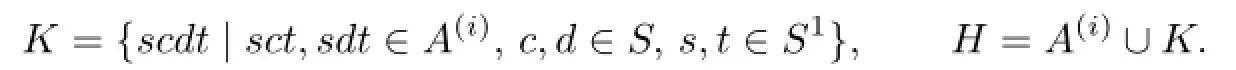
Consider the following cases:

(1)Ifa∈A(i),it is obvious thatα∈C;

(2)Ifa∈K,then we can saya=scdt,wheresct,sdt∈A(i),c,d∈S,s,t∈S1.SinceA(i)∈P(S),there existµ,ν∈Ysuch thatsct∈Gµ∩A(i)andsdt∈Gν∩A(i).It is easy to see thatµ,ν∈C.So we havea=scdt∈Gµνby the proof of Lemma 2.3.Sincea∈Gα, we haveα=µν∈C;

(3)Ifa∉H,then we havea=a1a2···asfor someai∈H(1≤i≤s).SinceH∈P(S), there exist anαi∈Ysuch that

It follows from(1)and(2)that

Then

Thus we haveα=α1α2···αs∈Csincea∈Gα.This shows that

and so

as required.

Theorem 2.4Let S=[Y;Gα;ϕα,β]be a Cli ff ord semigroup.Then

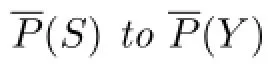
is a semiring isomorphism;

is a semiring homomorphism.

Proof.(a)Suppose thatAis a nonempty subset ofS,and

In the following,we prove thatφis an isomorphism in four steps.

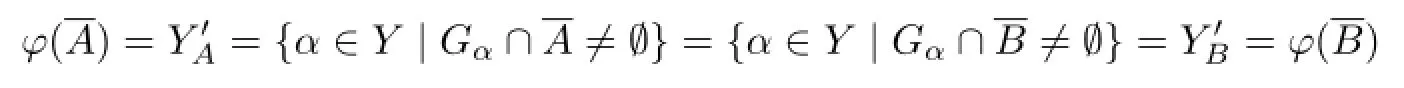
by Lemma 2.4.

We prove

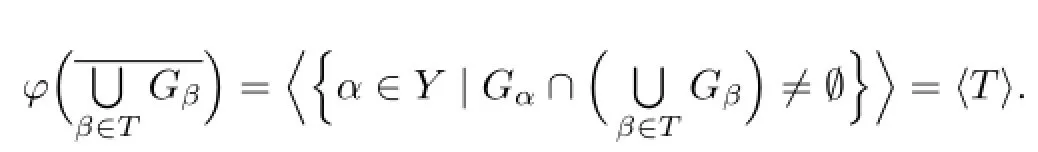
In fact,let

For allα∈I,there exists someβ∈Tsuch that

Since{Gα|α∈Y}is a family of disjoint groups,we haveα=β∈T.Therefore

Also,for allα∈T,

That is to say,α∈I.Therefore we haveT⊆I.SoT=I.It follows immediately that

i.e.,

(3)φis injective.Indeed,letand there existsµ∈Ysuch thata∈Gµ∩.Ifthenµ∈by Lemma 2.4.So we immediately have

(4)φis a homomorphism.Indeed,for allA,B∈P(S),by Lemma 2.4,we have

and

It is easy to prove that

So we have

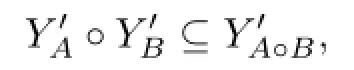
and so

On the other hand,for allγ∈H,there exista∈Aandb∈Bsuch that

andab∈Gγ,we have

i.e.,

(b)Sinceτ:is a semiring homomorphism,andφ:is a semiring isomorphism by(a),it is easy to see thatφ◦τ,i.e.,the composition ofφandτ,is a semiring homomorphism fromP(S)to.

[1]Zhao X Z.Idempotent semirings with a commutative additive reduct.Semigroup Forum,2002, 64:289–296.

[2]Ghosh S,Pastijn F,Zhao X Z.Varieties generated by ordered bands I.Order,2005,22:109–128.

[3]Pastijn F.Varieties generated by ordered bands II.Order,2005,22:129–143.

[4]Burris S,Sankappanavar H P.A Course in Universal Algebra.Berlin:Springer-Verlag,2000.

[5]Howie J M.An Introduction to Semigroup Theory.Scotland:Univ.of St.Andrews,1976.

tion:16Y60,20M07

A

1674-5647(2014)02-0097-09

10.13447/j.1674-5647.2014.02.01

Received date:April 9,2011.

Foundation item:The NSF(2010GZS0093)of Jiangxi Province.

E-mail address:469261217@qq.com(Fu Y Y).