Blow-up Sets to a Coupled Heat System

(1.Department of Mathematics,Liaoning University,Shenyang,110036)

(2.Department of Mathematical Sciences,Tsinghua University,Beijing,100084)

(3.School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024)

Blow-up Sets to a Coupled Heat System

WANG JIN-HUAN1,2AND HONG LIANG1,3

(1.Department of Mathematics,Liaoning University,Shenyang,110036)

(2.Department of Mathematical Sciences,Tsinghua University,Beijing,100084)

(3.School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024)

Communicated by Yin Jing-xue

This paper deals with a heat system coupled via local and localized sources subject to null Dirichlet boundary conditions.In a previous paper of the authors,a complete result on the multiple blow-up rates was obtained.In the present paper,we continue to consider the blow-up sets to the system via a complete classi fi cation for the nonlinear parameters.That is the discussion on single point versus total blow-up of the solutions.It is mentioned that due to the in fl uence of the localized sources, there is some substantial difficulty to be overcomed there to deal with the single point blow-up of the solutions.

coupled localized source,coupled local source,total blow-up,single point blow-up,blow-up set

1 Introduction

This paper considers the following heat system coupled via local and localized sources:

whereB={x∈RN:|x|＜1},p1,p2＞1,q1,q2＞0,the radial initial datau0,v0∈C2(B)∩C(¯B)satisfy

and

normalized byφ0＞0 inBand‖φ0‖∞=1.Obviously,φ0is a radially symmetric function with0 forr∈(0,1].Suchu0andv0do exist indeed(see[1–2]).

The theory of parabolic equations insures that there exists a unique local solution to (1.1),which blows up in fi nite time for large initial data,(see,e.g.,[3–5]).LetTbe the maximum existence time of the solution.

The system(1.1)is a combination of the following two coupled problems:with local coupling

and with localized coupling

subject to null Dirichlet boundary conditions,whereΩis a bounded domain.

It is well known that the blow-up solutions of(1.3)withp1p2＞1 must be single point blow-up(see[5–7]).In[5]the single point blow-up result was proved forn=1 with a very restrictive condition ofp1=p2.This restriction ofp1=p2was removed by Souplet[7], which is a substantially improvement for the single blow-up discussion.On the other hand, we know that the blow-up occurs everywhere inΩ=Bfor(1.4)withq1q2＞1(see[8]). Naturally,both total and single point blow-up may be possible for(1.1).

The total versus single point blow-up for the scalar equation with both local and localized sources

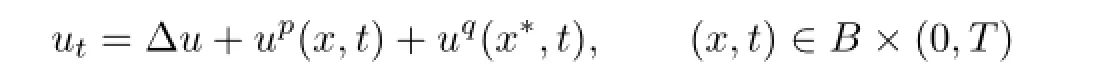
was well studied by Okadaet al.[9–10]As for system,little is known concerning the total and single point blow-up(see[1,11]).

This paper is arranged as follows:The next section gives the multiple blow-up rate results obtained in[12]as the preliminaries of the paper.Sections 3 and 4 are devoted to the discussion on total and single point blow-up,respectively.

2 Multiple Blow-up Rates

This section introduces some preliminaries to discuss blow-up sets.

The maximum principle with the assumptions(A)and(B)implies thatu,vare radial, and

Next,we introduce the multiple blow-up rate results for(1.1)obtained in[12].

Lemma 2.1([12],Theorem 2.1)Let(u,v)be a blow-up solution of(1.1).Then there exist constants c,C＞0such that

where(α,β)is de fi ned by

3 Total Blow-up

We deal with total blow-up of the solutions to(1.1)in this section.We know that the total blow-up of the solutions is caused by the localized sources.The discussion of total blow-up is carried out in three cases:(a)p1≤q1;(b)p2≤q2;(c)p1＞q1,p2＞q2.Denote

Letϕsolve the heat equation with the initial dataφ0de fi ned by(1.2):

The maximum principle yields

We give the following lemma without proof.

Lemma 3.1([11],Lemma 3.1)Let(u,v)be a solution of(1.1)with ϕ satisfying(3.2). Then

Theorem 3.1If p1≤q1(or p2≤q2),then the solution of(1.1)blows up everywhere.

Proof.Consider the casep1≤q1only.If,in addition,p2≤q2,it is easy to know from Lemma 2.1 that

Using(3.4)and(3.5)withq1q2＞1,we have

Thus,bothuandvblow up everywhere inB.

Ifp1≤q1withp2＞q2,by Lemma 2.1,

Combining(3.4)and(3.6)withq1p2＞1 yields

which implies thatuis total blow-up.

Next we give the blow-up set ofvby using the uniform rate estimate(3.7)ofu.Set

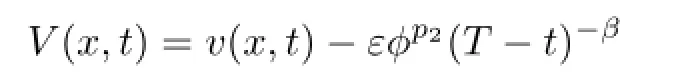
Together withV=0 on∂B×(0,T),we know

by the comparison principle.Thusvis total blow-up as well.The proof is completed.

Now treat the case with the local sources dominating the localized ones,i.e.,p1＞q1,p2＞q2,for which

Proof.Prove only the total blow-up foru.By Lemma 2.1,

We have

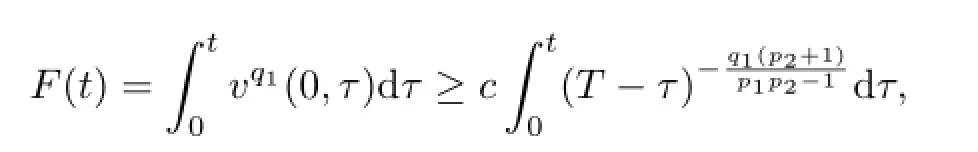
and so

which implies thatublows up everywhere inBby Lemma 3.1.

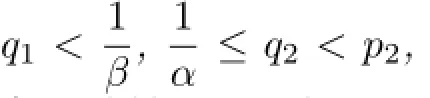
Proof.Prove the case(i)only.We know from the proof of Theorem 3.2 thatuis of total blow-up,and

Set

By a discussion similar to Theorem 3.1,takingεsufficiently small,we deduce that

4 Single Point Blow-up

Just like in[7,13–14],de fi ne the(backward)similarity variables around(b,T)in

Then,wandzsatisfy

Set

and denote by(T(s))s≥0the semigroup associated withL.More precisely,for eachφ∈L∞(Rn),set

wherewis the unique classical solution of

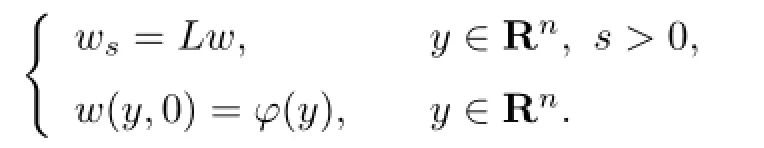
Put

By the Jensen’s inequality,

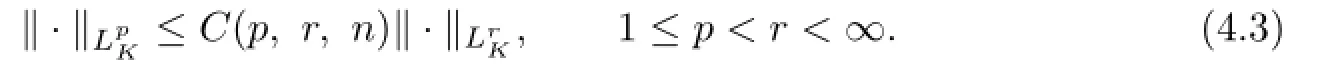
Note that if the functionφis de fi ned only on a sub-domain of Rn,thendenotes the norm of the extension ofφby 0.Some important properties of(T(s))s≥0are given by the following lemma.

Lemma 4.1([7],Lemma 3.1) (i)For all1≤r＜∞,

(ii)For all1≤m＜r＜∞,there exist C0,s∗＞0such that

Further,we have the following proposition.

Proposition 4.1Let M＞0and(u,v)be a classical solution of(1.1)satisfying

for some σ≥s0,then a is not a blow-up point of(u,v).

For givens1＞max{s0,s′},denote bythe zero-extensions ofw,z,respectively,where (w,z)is the solution of(4.2).By the variation of constants formula with(4.6),we have that

and

On the other hand,by(4.6),we have

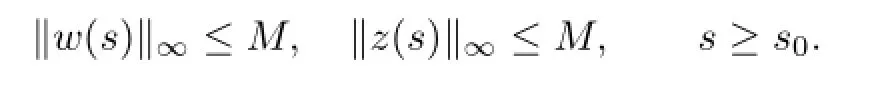
Seth:=˜w+˜z.Then

where

Thus

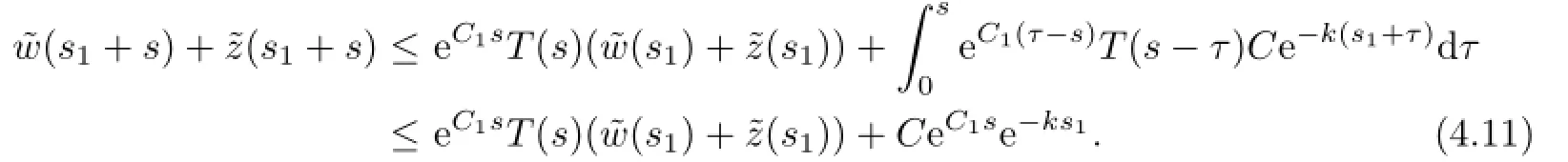
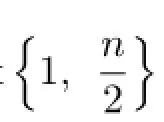
Now let

To proveT0=∞,suppose for contradiction thatT0＜∞.Without loss of generality, assume thatp1≤p2,i.e.,α≤β.By(4.13)and(4.12),we have

For 0≤τ≤T0,(4.11),(4.5),(4.8)and(4.14)imply that

whereCis independent ofa.By(4.9)withs1=σ+s∗,(4.4),(4.3)and(4.15),we deduce that

Similarly,by(4.10)withαp2＞β,we have

Using(4.16)and(4.17)fors=T0,and(4.12)withs=s∗,we deduce

and hence

which is impossible forε＞0 sufficiently small.This concludes

In particular,it follows from(4.15)that

By continuity ofu,there exists aδ＞0 so small that(4.7)is still true for anyb∈Bsatisfying|b−a|＜δ(note thatεandCare independent ofa),and hence(4.18)holds,which implies that

Consider the ordinary di ff erential equation system

Proposition 4.2([7],Proposition 4.1) (a)Let(w,z)be a global nonnegative solution of(4.19)for all s∈R.Then one of the following statements is true:

(i)(w,z)≡(0,0);

(ii)(w,z)≡(A0,B0);

(b)Let s0∈Rand w,z∈C1([s0,T)),w,z≥0,satisfy

together with w(s0)≥A0,z(s0)≥B0,and(w(s0),z(s0))≠(A0,B0).Then T＜∞.

Set

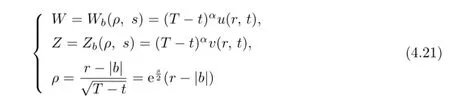
for(ρ,s)∈.

Assume for contradiction that there exists anr0∈(0,1)satisfying

We need the following key lemma.

uniformly on[0,|a|]for each a∈Br0.

Proof.We fi rst considera∈Br0{0},and then treata={0}.

Leta∈Br0{0},and(W,Z)=(Wa,Za)be the solution of(4.22).By the upper estimates(4.20),we know thatWandZare bounded.Fix a sequencesj→∞,and let the sequence(Wj,Zj)be the form of

For some subsequence(still denoted bysj),by(4.22)and the parabolic estimates,it follows that(Wj,Zj)converges to(φ,ψ)uniformly on compact subsets of R×R and such that

Sinceur,vr≤0 on[0,1),

So,we have

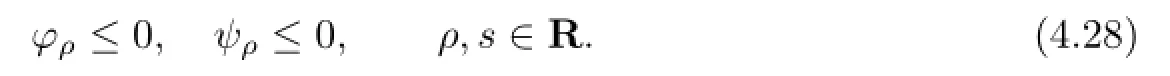
De fi ne

Obviously,

As in[7],by using a standard argument based on multiplication by test functions with a new similarity variables,we know thatφ±,ψ±satisfy {

In view of Proposition 4.2(a),only two cases can occur:

so

and hence

or

If the fi rst case occurs,then for alltj→T,there exists a subsequence such that

Hence(4.24)holds,and(4.25)is obtained.

Now we show that the second case is impossible.Otherwise,setb:|a|＜|b|＜r0,and let(wb,zb)and(Wb,Zb)be,respectively,the re-scaling and the radial re-scaling of(u,v) by similarity variables around(b,T).In fact,by assumption

Similarly to the arguments for Lemma 3.1 in[11],we can prove that for anyε＞0,there exists someσsuch that

which with Proposition 4.1 implies thatu(b,t)andv(b,t)is bounded ast→T,a contradiction.

Fora={0},by the results for 0＜|a|＜r0,similarly to[7],we can deduce(4.24).The proof is completed.

Now we can prove the single point blow-up conclusion as follows:

Proof.Under the assumptions of the theorem,we know the blow-up rate estimates(4.20) by Lemma 2.1,and thus

Suppose for contradiction that there exists a blow-up point withr0∈(0,1)such that

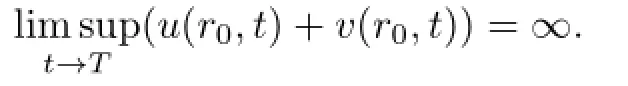
ThenJ,Gsatisfy

and consequently,

where

Similarly,

where

Noticingd=Kc,we have

and

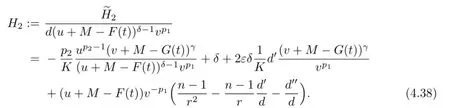
By(4.23),there exists aτ＞0 such that for allt∈[τ,T),

Thus,

Without loss of generality,assume thatp1≤p2.Chooseγ,δsuch that 1＜γ＜p1, 1＜δ＜p2,and

i.e.,

By(4.39)–(4.41),for anyε＞0 small there existsτ0close toT,such that

Similarly,

Combining(4.35)and(4.36),we see thatJandIsatisfy

for 0＜r＜|a|,τ0＜t＜T.

Moreover,since,for instance,ur(r,t)＜0 for(r,t)∈(0,1]×(0,T),andurr(0,t),vrr(0,t)＜0 in(0,T),takingε＞0 sufficiently small,we get

In addition,by the de fi nitions ofJandI,we have

The maximum principle with(4.42)–(4.44)implies that

On the other hand,Lemma 4.2 implies that

for someτ2∈(τ0,T).Without loss of generality,assumep1≤p2.The fi rst inequality in (4.46)implies that

and hence

which along with(4.46)yields

This contradicts(4.23).The proof is completed.

[1]Zheng S N,Wang J H.Total versus single point blow-up in heat equations with coupled localized sources.Asymptotic Anal.,2007,51:133–156.

[2]Rossi J D,Souplet P.Coexistence of simultaneous and non-simultaneous blow-up in a semilinear parabolic system.Di ff erential Integral Equations,2005,18:405–418.

[3]Galaktionov V A,Kurdyumov S P,Samarskii A A.A parablic system of quasilinear equations I.Di ff erential Equations,1983,19:2123–2140.

[4]Galaktionov V A,Kurdyumov S P,Samarskii A A.A parablic system of quasilinear equations II.Di ff erential Equations,1985,21:1544–1559.

[5]Friedman A,Giga Y.A single pint blow-up for solutions of semilenear parabolic systems.J. Fac.Sci.Univ.Tokyo Sect.IA Math.,1987,34:65–79.

[6]Herrero M A,Vel´azquez J J.Blow-up behavious of one-dimensional semilincar parabolic equations.Ann.Inst.H.Poincar´e Anal.Non Lin´eaire,1993,10:131–189.

[7]Souplet P.Single-point blow-up for a semilinear parabolic system.J.European Math.Soc., 2009,11:169–188.

[8]Pedersen M,Lin Z G.Coupled di ff usion systems with localized nonlinear reactions.Comput. Math.Appl.,2001,42:807–816.

[9]Okada A,Fukuda I.Total versus single point blow-up of a semilinear parabolic heat equation with localized reaction.J.Math.Anal.Appl.,2003,281:485–500.

[10]Fukuda I,Suzuki R.Blow-up behavior for a nonlinear heat equation with a localized source in a ball.J.Di ff erential Equations,2006,218:273–291.

[11]Wang J H,Zheng S N.Total versus single point blow-up in a localized heat system.Front. Math.China,2010,5:341–359.

[12]Wang J H,Hong L.Multiple blow-up rates to a coupled heat system.J.Math.Res.Exposition, in press.

[13]Andreucci D,Herrero M A,Vel´azquez J J.Liouville theorems and blow up behavious in semilinear reaction di ff usion systems.Ann.Inst.H.Poincar´e Anal.Non Lin´eaire,1997,14: 1–53.

[14]Giga Y,Kohn R V.Asymptotically self-similar blow-up of semilinear heat equations.Comm. Pure Appl.Math.,1985,38:297–319.

tion:35K55,35B33

A

1674-5647(2014)02-0117-14

10.13447/j.1674-5647.2014.02.03

Received date:Oct.13,2011.

Foundation item:China Postdoctoral Science Foundation(20110490409)and Science Foundation(L2010146) of Liaoning Education Department.

E-mail address:wjh800415@163.com(Wang J H).