Pseudo Almost Automorphic Solutions for Non-autonomous Stochastic Di ff erential Equations with Exponential Dichotomy

(School of Mathematics,Jilin University,Changchun,130012)

Pseudo Almost Automorphic Solutions for Non-autonomous Stochastic Di ff erential Equations with Exponential Dichotomy

DU JIN-SHI,SUN KAI AND WANG YAN

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Li Yong

In this paper,we consider the existence and uniqueness of the solutions which are pseudo almost automorphic in distribution for a class of non-autonomous stochastic di ff erential equations in a Hilbert space.In conclusion,we use the Banach contraction mapping principle and exponential dichotomy property to obtain our main results.

pseudo almost automorphy,exponential dichotomy,non-autonomous stochastic di ff erential equation

1 Introduction

Liu and Sun[1]introduced the concept of almost automorphy in distribution and studied the almost automorphy in distribution solutions of stochastic di ff erential equations driven by L´evy noise.Chen and Lin[2]researched the square-mean pseudo almost automorphic process and its applications.

In this paper,we consider the existence and uniqueness of the solutions which are pseudo almost automorphic in distribution for a class of non-autonomous stochastic di ff erential equations of the form

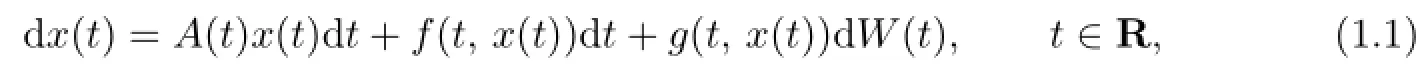
whereA(t)is a family of closed linear operators satisfying the Acquistapace-Terrani conditions(see[3–4]),f(t,x),g(t,x)are square-mean pseudo almost automophic int∈R foreachx∈L2(P,H),andf,gare assumed to satisfy Lipschitz conditions with respect tox.

This paper is organized as follows.In Section 2,we provide de fi nitions,lemmas and propositions.In Section 3,we prove our main result.

2 Preliminaries

In this section,we provide some preliminaries.The readers may fi nd more details in[1–9].

2.1 The Norm of the Space

Throughout this paper,we assume that(H,‖·‖)is a real separable Hilbert space.Let (Ω,F,P)be a complete probability space.The notationL2(P,H)stands for the space of allH-valued random variablesxsuch that

Forx∈L2(P,H),let

Then it is routine to check thatL2(P,H)is a Hilbert space equipped with the norm‖·‖2. LetW(t)be a two-sided standard one-dimensional Brownian motion de fi ned on the fi ltered probability space(Ω,F,P,Ft),whereFt=σ{W(u)−W(v);u,v≤t}.

2.2 Square-mean Pseudo Almost Automorphic

De fi nition 2.1[1]A stochastic process x:R→L2(P,H)is said to be L2-continuous if for any s∈R,

Note that if anH-valued process isL2-continuous,then it is necessarily stochastically continuous.

De fi nition 2.2[2]A stochastic process x:R→L2(P,H)is said to be L2-bounded if there exists an M＞0such that

The collection of allL2-bounded continuous processes is denoted bySBC(R;L2(P,H)).

De fi nition 2.4[1]An L2-continuous stochastic process x:R→L2(P,H)is said to besquare-mean almost automorphic if every sequence of real numbers{}has a subsequence{sn}such that for some stochastic processes y:R→L2(P,H),andhold for all t∈R.

The collection of all square-mean almost automorphic stochastic processesx:R→L2(P,H)is denoted byAA(R;L2(P,H)).

De fi nition 2.5[2]An L2-continuous process f(t):R→L2(P,H)is said to be squaremean pseudo almost automorphic if it can be decomposed as

The collection of all square-mean pseudo almost automorphic processesf(t):R→L2(P,H)is denoted bySPAA(R;L2(P,H)).

Lemma 2.1[8]If x,x1and x2are all square-mean almost automorphic stochastic processes, then the following statements hold:

(1)x1+x2is square-mean almost automorphic;

(2)λx is square-mean almost automorphic for every scalar λ;

Lemma 2.2[8]AA(R;L2(P,H))is a Banach space when it is equipped with the norm

Lemma 2.3[2]SBC0(R;L2(P,H))is a Banach space with the norm‖·‖∞.

Lemma 2.4[2]SPAA(R;L2(P,H))is a Banach space with the norm‖·‖∞.

De fi nition 2.6[8]A function f:R×L2(P,H)→L2(P,H),(t,x)(t,x),which is jointly continuous,is said to be square-mean almost automorphic in t∈Rfor eachx∈L2(P,H),if for every sequence of real numbers{}there exists a subsequence{sn}such that for some function˜f,andhold for all t∈Rand each x∈L2(P,H).

Proposition 2.1[8]Let f:R×L2(P,H)→L2(P,H),(t,x)→f(t,x)be square-mean almost automorphic in t∈Rfor each x∈L2(P,H).Assume that f satis fi es Lipschitz condition in the following sense:

where M＞0is independent of t.Then for any square-mean almost automorphic process x:R→L2(P,H),the stochastic process F:R→L2(P,H)given by F(t):=f(t,x(t))is square-mean almost automorphic.

Proposition 2.2[2]Let f(t,x)∈SPAA(R×L2(P,H),L2(P,H)).Assume that f satis fi es Lipschitz condition in the following sense:

where M＞0is independent of t.Then f(t,x(t))∈SPAA(R;L2(P,H))for any x∈SPAA(R;L2(P,H)).

2.3 Acquistapace-Terrani Condition and Exponential Dichotomy

Proposition 2.3[3–5]If the Acquistapace-Terreni condition(ATC)is satis fi ed,that is, there exists a constant K0＞0and a set of real numbers α1,α2,···,αk,β1,β2,···,βkwith0≤βi＜αi≤2,i=1,2,···,k,such that

where

and there exists a constant K1≥0such that

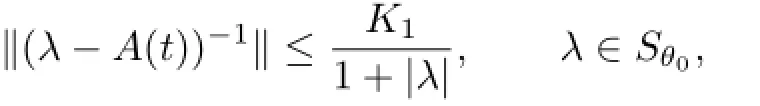
then there exists a unique evolution family{U(t,s),t≥s＞−∞}on L2(P,H).

We assume that ATC is satis fi ed in the rest of this paper.

LetBbe a Banach space.We denote byLb(B)the Banach space of all bounded linear operators fromBtoBequipped with natural operator norm.

De fi nition 2.7[7,10]A family of bounded linear operators{U(t,s):t≥s,t,s∈R}on L2(P,H)associated with A(t)is said to be an evolution family of operators if the following conditions hold:

(1)U(t,s)U(s,r)=U(t,r)for every t≥s≥r;

(2)U(t,t)=I for all t∈R;

(3)(t,s)→U(t,s)∈Lb(L2(P,H))is strongly continuous for every t＞s;

De fi nition 2.8[10]An evolution family{U(t,s):t≥s,t,s∈R}is said to exponential dichotomy(ED),if there are projectors P(t),t∈R,being uniformly bounded and strongly continuous in t and two constants K≥1and ω＞0such that

(1)P(t)U(t,s)=U(t,s)P(s);

(2)the restriction U(s,t):Q(s)L2(P,H)→Q(t)L2(P,H)of U(t,s)is invertible,and U(t,s)=(U(s,t))−1,t≥s;

where Q(s)=I−P(s).

De fi nition 2.9An L2-continuous stochastic process x(t)t∈Ris called a mild solution of the problem(1.1)if it satis fi es the corresponding stochastic integral equation:

for all t≥a0and for each a0∈R.

LetP(H)be the space of all Borel probability measures onHendowed with theβmetric:

wherefis a Lipschitz continuous real-valued function onHwith the norms

De fi nition 2.10[1]An H-valued stochastic process X(t)is said to be almost automorphic in distribution if its lawµ(t)is a P(H)-valued almost automorphic mapping,i.e.,for everysequence of real numbers{},there exist a subsequence{sn}and a P(H)-valued mapping(t)such that

hold for all t∈R.

De fi nition 2.11An L2-continuous process f(t):R→L2(P,H)is said to be pseudo almost automorphic in distribution,if it can be decomposed as f=g+φ,where g is almost automorphic in distribution and φ∈SBC0(R;L2(P,H)).

2.4 A Variant of Gronwall’s Lemma

Refering to[6]and[9],we have the following version of Gronwall’s lemma.

Lemma 2.5Let g:R→Rbe a bounded and continuous function such that for all t∈R,

where α:R→Ris a bounded function and satis fi es

β1,···,β2n≥0are constants and δ1,···,δ2n＞2β+ξ are constants with

Let

Then for every γ∈(0,δ−2β−ξ]we have

where

Proof.Let

Then

Let

Then fort∈RS,(2.5)is always true.Let

Thenν(t)is nonnegative and bounded.Fort∈S,we have

Therefore,

i.e.,fort∈S,

Fort∈RS,byν(t)=0,we have

Hence,for allt∈R,

i.e.,there existst0≥0 such that for allt≥t0,

Then

Lettingt→+∞,we have

which is a contradiction.

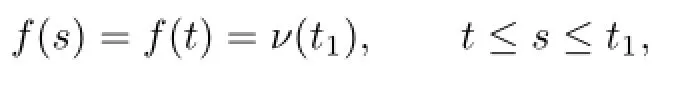
and

Then

By a proof similar to that of Lemma 3.3 in[6],we have

Then

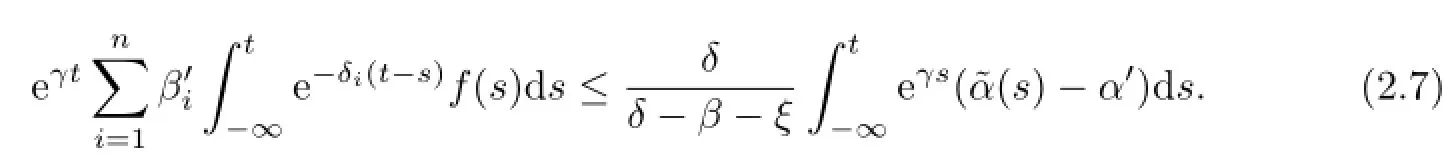
Substituting(2.7)into(2.6)yields

Since

we have

3 Main Result

3.1 Assumptions

In order to get our result,we make the following assumptions:

(H1)The problem(1.1)satis fi es an exponential dichotomy.There exists an invariant projectorP(t)of the evolution familyU(t,s)generated byA(t),and constantsM≥1 andω＞0 such that

and

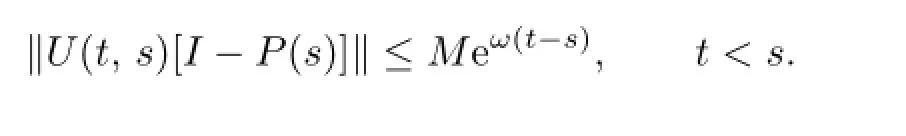
moreover,

(H3)The functionsfandgare square-mean pseudo almost automorphic int∈R for eachx∈L2(P,H),and there exist positive numbersLfandLgsuch that for anyx,y∈L2(P,H),

The functionsfandgcan be decomposed as

anda,b,α,βsatisfy Lipschitz condition with respect toxuniformly int,that is,there exist positive numbersLa,Lb,Lα,Lβsuch that

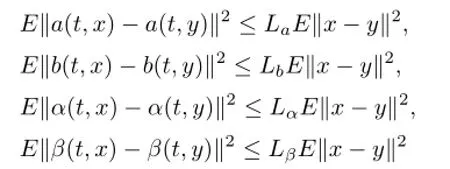
for allt∈R andx,y∈L2(P,H).

3.2 Theorem

Theorem 3.1If(H1)–(H3)are satis fi ed,then(1.1)has a unique L2-bounded mild solution provided that

Furthermore,this unique L2-bounded solution is pseudo almost automorphic in distribution provided that

Proof.Note that

is well de fi ned for eacht∈R and satis fi es(2.3).And if it isL2-bounded,then it is a mild solution of(1.1).Similarly to[1],we divide the proof into three steps.

Step 1.AnL2-bounded solution is necessarilyL2-continuous.

It follows from(H1)that there exist constantsM＞0 andω＞0 such that

and

Ifx(t)is anL2-bounded solution,i.e.,(3.3)holds,then it follows from Cauchy-Schwarz inequality and Itˆo’s isometry that fort≥r,

From the de fi nition ofU(·,·),we know that for anyx∈H,

Note that

by Lebesgue dominated convergence theorem,we have

Under the conditions of the theorem andX(·)isL2-bounded,by Lemma 2.2 we have

Similarly to(3.4),we can get

Hence

The similar argument yields that

that is,x(·)isL2-continuous.

Step 2.The existence and uniqueness of anL2-bounded solution.

Denote byCb(R;L2(P,H))the Banach space of all boundedL2-continuous mapping from R toL2(P,H)endowed with the norm‖·‖∞.Let us consider the operatorϕacting onCb(R;L2(P,H))de fi ned by

According to(H1),(3.4)and(3.5),ϕx(·)is anL2-bounded process if so isx(·).Then,by the proof of Step 1,ϕx(·)is anL2-continuous process ifx(·)is anL2-bounded process.It follows that the operatorϕmapsCb(R;L2(P,H))into itself.For anyx,y∈Cb(R;L2(P,H))and eacht∈R,we prove thatϕis a contraction mapping onCb(R;L2(P,H)).

We have

And in the same way,we have

By Itˆo’s isometry property of stochastic integrals,we have

Similarly,we can get

So we can conclude that,for allt∈R,

Let

Then

This means thatϕis a contraction mapping whenL0＜1.Therefore,there exists a uniquex(·)such thatϕx=x,which is the uniqueL2-bounded mild solution to(1.1).

Step 3.Pseudo almost automorphy of theL2-bounded solution.

For givenx∈SPAA(R;L2(P,H)),by the de fi nition of the mappingϕ,we have

Let us prove that the mappingΓxis almost automorphic in distribution,and thatΩx∈SBC0(R;L2(P,H)).

First,by the proof of Step 1,it can be easily proved thatΓx(·)isL2-continuous process ifx(·)is anL2-bounded process.

By Theorem 2.1 and Proposition 2.1,we havea(t,x(t)),α(t,x(t))∈AA(R;L2(P,H)).Letbe an arbitrary sequence of real numbers.There exist a subsequence{sn}n∈Nofand stochastic processes˜a,˜αsuch that

hold for allt∈R.Let˜x(·)satisfy the equation

By the proofs of Steps 1 and 2,(3.7)has a uniqueL2-bounded solution.

Let

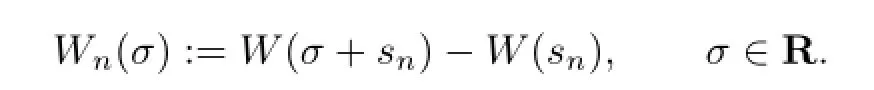
ThenWnis also a Wiener process with the same law asW.Letσ=r−sn.Then we have

In the similar way to[6],we have

It follows thatΓx(t+sn)has the same distribution asxn(t)for eacht∈R andxn(t)is unique andL2-bounded.By(H2),for anyε＞0,there exists anN∈N such that for alln＞N,we have

Moreover,we de fi ne

Then we have

with

Note that

By means of Lemma 2.2,we have

and consequently,

Sinceais square-mean almost automorphic int,εis arbitrary and(·)is bounded inL2(P,H),by Lebesgue dominated convergence theorem,we have that

In a similar way,we can also conclude that

with

By Itˆo’s isometry,we obtain

with

Similarly,we can conclude that

with

By above estimations,we have

with

By Lemma 2.5 and(3.2),it follows thatE‖xn(t)−(t)‖2→0 asn→∞for eacht∈R.

SinceΓx(t+sn)has the the same distribution asxn(t),it follows thatΓx(t+sn)→(t) in distribution asn→∞.And we can show in the same way that˜x(t−sn)→Γx(t)in distribution asn→∞for eacht∈R.

Then,we prove thatΩmapsSBC0(R;L2(P,H))into itself.

By using the arguments above,we know thatΩxis anL2-continuous process.Sinceb,β∈SBC0(R;L2(P,H)),it can be proved thatΩxisL2-bounded,i.e.,Ωx∈SBC(R;L2(P,H)). Hence,we only need to prove

Note that

A simple calculation yields that

Similarly,we haveΩ2→0 asT→∞.On the other hand,

Similarly,we haveΩ4→0 asT→∞.

So far,we have veri fi ed

i.e.,Ωx∈SBC0(R;L2(P,H)).Therefore,ϕxis pseudo almost automorphic in distribution.

Acknowledgement The authors sincerely thank Professor Liu Zhen-xin for his encouragement and helpful discussions.

[1]Liu Z,Sun K.Almost automorphic solutions for stochastic di ff erential equations driven by Levy noise.J.Funct.Anal.,2014,266:1115–1149.

[2]Chen Z,Lin W.Square-mean pseudo almost automorphic process and its application to stochastic evolution equations.J.Funct.Anal.,2011,261:69–89.

[3]Acquistapace P.Evolution operators and strong solution of abstract linear nonautonomous parabolic equations.Di ff erential Integral Equations,1988,1:433–457.

[4]Acquistapace P,Terreni B.A uni fi ed approach to abstract linear nonautonomous parabolic equations.Rend.Sem.Mat.Univ.Padova,1987,78:47–107.

[5]Chang Y,Zhao Z,N’Gu´er´ekata G M.Square-mean almost automorphic mild solutions to nonautonomous stochastic di ff erential equations in Hilbert spaces.Comput.Math.Appl.,2011, 61:384–391.

[6]Kamenskii M,Mellah O,Raynaud De Fitte P.Weak averaging of semilinear stochastic di ff erential equations with almost periodic coe ff cients.arXiv:1210.7412v2[math.PR].Submitted on 28 Oct.2012.

[7]Bezandry P H,Diagana T.Square-mean almost periodic solutions nonautonomous stochastic di ff erential equations.Electron.J.Di ff erential Equations,2007,117:1–10.

[8]Fu M,Liu Z.Square-mean almost automorphic solutions for some stochastic di ff erential equations.Proc.Amer.Math.Soc.,2010,138:3689–3701.

[9]Deng S,Zhang W.Remarks on projected gronwall inequality(in Chinese).J.Math.Res. Exposition,2002,22:307–313.

[10]Cui J,Yan L.On almost automorphic mild solutions for nonautonomous stochastic evolution equations.Abstr.Appl.Anal.,2012,2012:Article ID 870831,25pp.

tion:60H25,34C27,34F05,34G20

A

1674-5647(2014)02-0139-18

10.13447/j.1674-5647.2014.02.05

Received date:Oct.9,2012.

Foundation item:The Undergraduate Research Training Program Grant(J1030101)and the NSF(11271151) of China.

E-mail address:djs052611@sina.cn(Du J S).