Existence of Solution for Fractional Di ff erential Problem with a Parameter

SHI AI-LING1AND ZHANG SHU-QIN2,

(1.School of Science,Beijing University of Civil Engineering and Architecture,Beijing,100044)

(2.Department of Mathematics,China University of Mining and Technology,Beijing,100083)

Existence of Solution for Fractional Di ff erential Problem with a Parameter

SHI AI-LING1AND ZHANG SHU-QIN2,*

(1.School of Science,Beijing University of Civil Engineering and Architecture,Beijing,100044)

(2.Department of Mathematics,China University of Mining and Technology,Beijing,100083)

Communicated by Li Yong

We apply the method of lower and upper solutions combined with monotone iterations to fractional di ff erential problem with a parameter.The existence of minimal and maximal solutions is proved for the fractional di ff erential problem with a parameter.

Caputo derivative,parameter,monotone iterative method

1 Introduction

We consider the following fractional di ff erential problem with a parameter:

where 0＜T＜+∞,λ∈R,f∈C([0,T]×R×R,R),G∈C(R×R,R),u0∈R,andDαis Caputo fractional derivative of order 0＜α＜1 de fi ned by

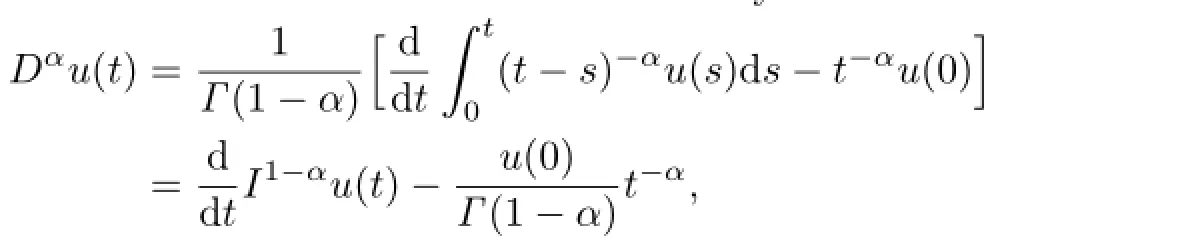
where

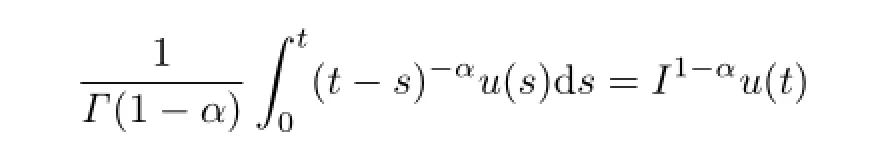
is the Riemann-Liouville fractional integral of order 1−α(see[1]).

Integer order di ff erential problem with a parameter has been studied for many years(see [2]).Di ff erential equations of fractional order occur more frequently on di ff erent research areas and engineering,such as physics,chemistry,control of dynamical,etc.Recently, many authors pay attention to the existence result of solutions of initial value problem for fractional di ff erential equations(see[3–15]).Motivated by[9–15],we consider the existence of the minimal and maximal solutions of(1.1),employing the classical proofs of di ff erential equations-monotone iterative method.

De fi nition 1.1We say that a pair(u,λ)∈Cα([0,T],R)×Ris a solution of(1.1)if(u,λ)satis fi es(1.1),where

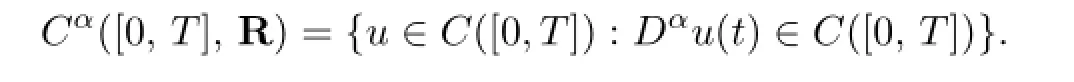
Lemma 1.1([1],Lemma 2.22)If f(t)∈AC([0,T])or f(t)∈C([0,T]),and0＜α＜1, then

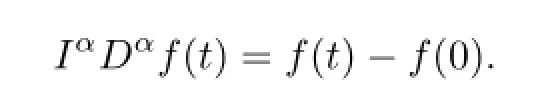
Lemma 1.2([1],Lemma 2.3)IpIqf(t)=Ip+qf(t),f∈L([0,T]),p,q＞0.

The following lemma is an existence result of solution for the linear initial value problem for a fractional di ff erential equation,which is important for us to obtain the existence result of solution for(1.1).

Lemma 1.3([1],Theorem 4.3)The linear initial value problem

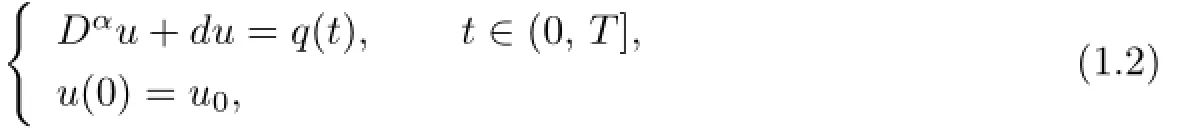
where d is a constant and q∈C([0,T]×R),has a unique solution u(t)∈Cα([0,T],R), and this solution is given by

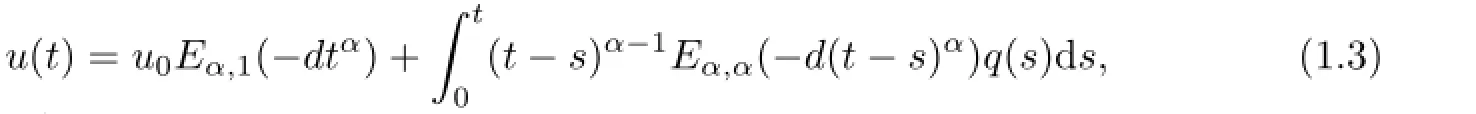
where Eα,α(−dtα)is Mittag-Leffler function.

In particular,when d=0,the initial value problem(1.2)has a solution

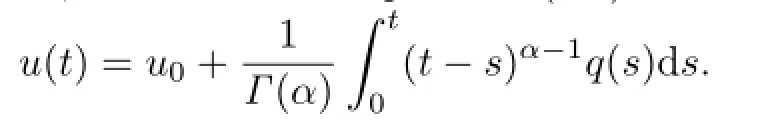
2 Main Result

In this section,we devote to considering the existence result of the minimal and maximal solutions of(1.1),by means of the monotone iterative method.

The following is the de fi nition of the upper and lower solutions of(1.1).

De fi nition 2.1A pair(v,µ)∈Cα([0,T],R)×Ris called a upper solution of(1.1),if it satis fi es

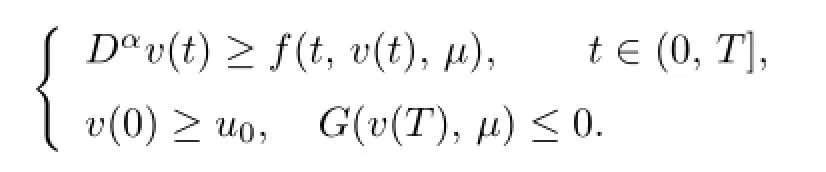
Analogously,the function(w,ν)∈Cα([0,T],R)×Ris called a lower solution of(1.1), if it satis fi es

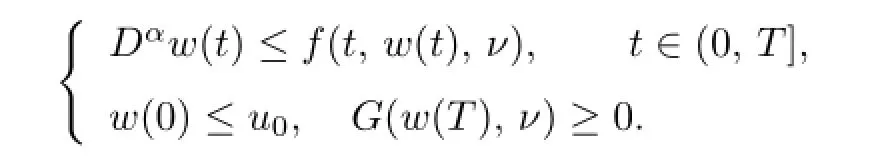
The following result plays a very important role in our next analysis.

Lemma 2.1If w∈Cα([0,T],R)satis fi es:

where

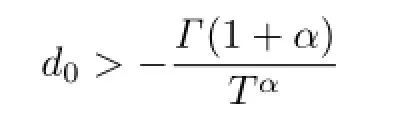
is a constant,then

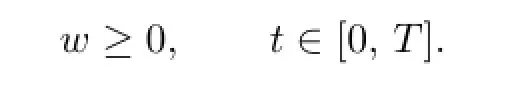
Proof.We assume by contradiction that the conclusion is not true,then there exist two pointst0,t1∈(0,T]such that

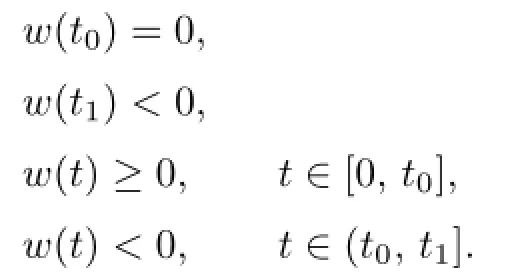
Assume thatt2is the fi rst minimal point ofw(t)on[t0,t1].

Firstly,we verify the result ford0＞0.It follows from(2.1)that

Hence,we have

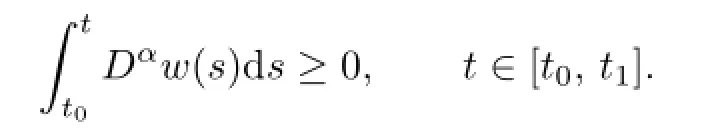
From the de fi nition of Riemann-Liouville fractional derivative,we obtain that

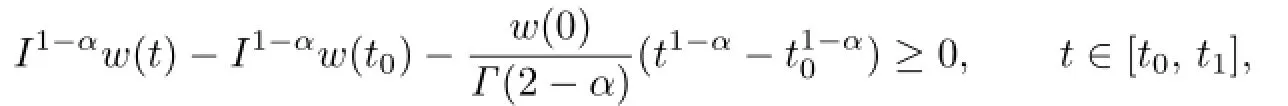
which implies that

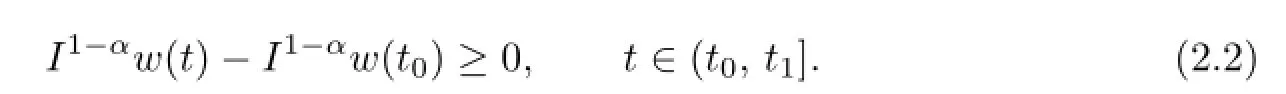
On the other hand,fort∈(t0,t1],we have

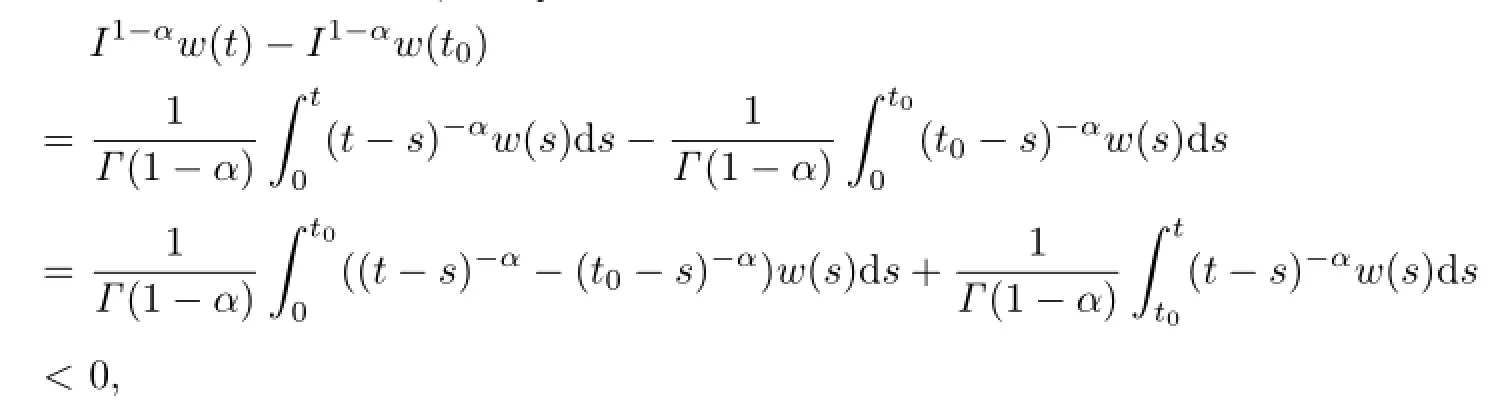
which contradicts(2.2).

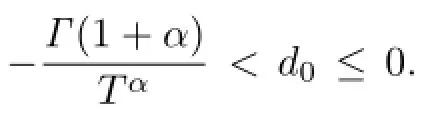
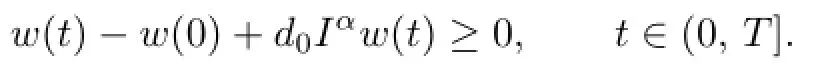
Hence

It follows that

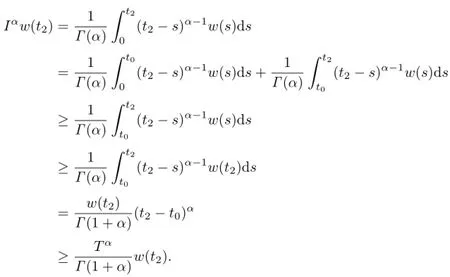
That is,

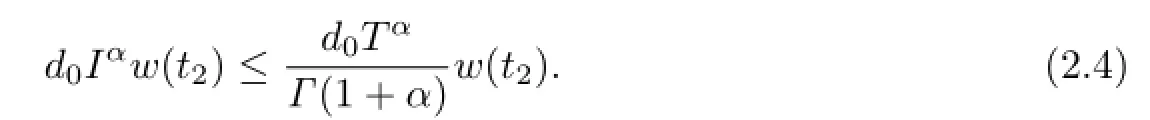
Thus,from(2.3)and(2.4),we have

This contradicts the negative property ofw(t2),since

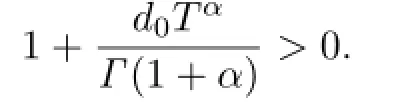
Thus,we complete the proof.

Theorem 2.1Let f∈C([0,T]×R×R,R),G∈C(R×R,R).Assume that

1°(y0,λ0),(z0,γ0)∈Cα([0,T],R)×Rare the lower and upper solutions of(1.1)such that y0(t)≤z0(t),t∈[0,T]and λ0≤γ0;

2°f(t,u1,λ)−f(t,u2,λ)≥−M(u1−u2),y0≤u2≤u1≤z0,λ0≤λ≤γ0,M＞0;

3°f(t,u,λ1)−f(t,u,λ2)≥P(λ1−λ2),λ0≤λ2≤λ1≤γ0,y0≤u≤z0,P＞0;

4°G(u1,λ)−G(u2,λ)≥Q(u1−u2),y0≤u2≤u1≤z0,λ0≤λ≤γ0,Q＞0;

5°G(u,λ1)−G(u,λ2)≥−N(λ1−λ2),λ0≤λ2≤λ1≤γ0,y0≤u≤z0,N＞0.

Then there exist monotone sequences{yn,λn}and{zn,γn}such that

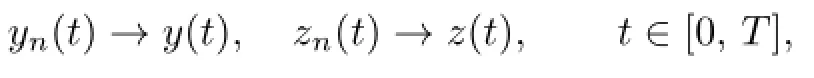
and

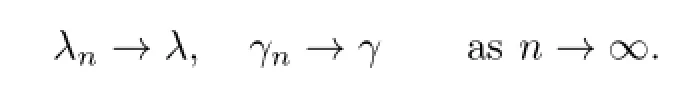
Moreover,(y,λ)and(z,γ)are the minimal and maximal solutions of(1.1),respectively.

Proof.It is easy to see that(1.1)is equivalent to the following problem:

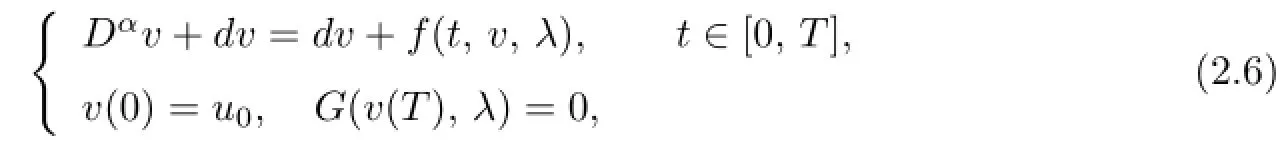
wheredis a given constant.This proof consists of fi ve steps as follows.

Step 1.Constructing sequences.

In order to apply the monotone iterative to study the existence of the minimal and maximal solutions of(1.1),we construct sequences(zk(t),γk),(yk(t),λk),k=1,2,···with the following iteration process(with(y0,λ0)and(z0,γ0)being the initial iteration):

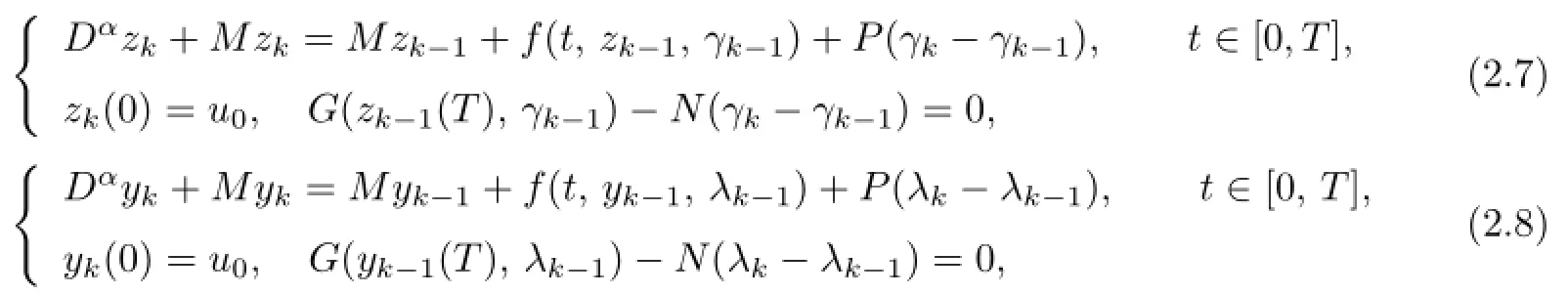
whereM,P,Nare the constants in the conditions 2°,3°,5°.From(2.7)and(2.8),we know that the sequences{γk}and{λk}are well de fi ned.Hence,combining with the assumptionf∈C([0,T]×R×R,R),by Lemma 1.3,we know that the sequences{zk}and{yk}are also well de fi ned.Moreover,by Lemma 1.3 and the continuity assumptions onf,we can easily obtain thatzk,yk∈Cα([0,T],R),k=1,2,···

Step 2.Monotone property of the sequences.

The sequences{yk},{λk},{zk}and{γk}constructed by(2.7)and(2.8)process the monotone property as follows:

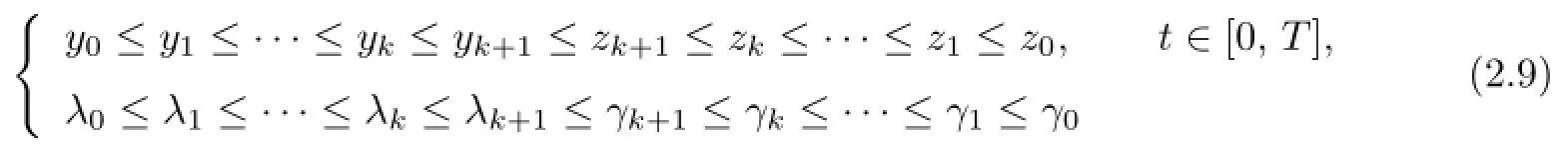
fork=1,2,···

In fact,let

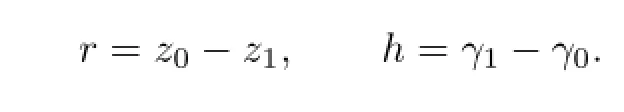
By(2.7)and De fi nition 2.1,one has

which implies thath≤0,i.e.,γ1≤γ0;moreover,by(2.7)andh≤0,we have

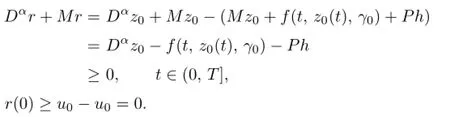
In view of Lemma 2.1,we have

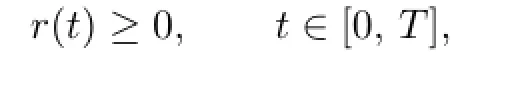
which leads to

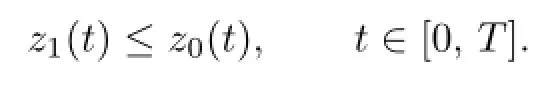
Let

By(2.8)and De fi nition 2.1,one has

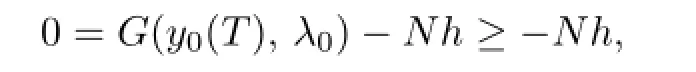
which implies thath≥0,i.e.,λ1≥λ0;moreover,by(2.8)andh≥0,we have

In view of Lemma 2.1,we have

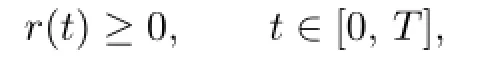
which leads to

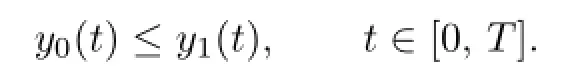
Let

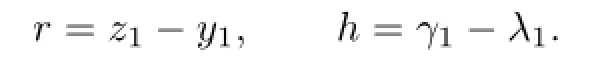
By(2.7),(2.8),y0≤z0,λ0≤γ0and 4°,5°,one has

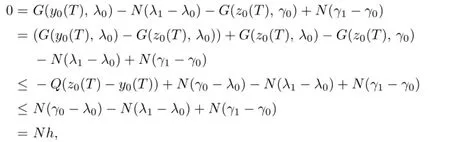
which implies thath≥0,i.e.,λ1≤γ1;moreover,by(2.7),(2.8),y0≤z0,λ0≤γ0,2°,3°, andγ1≥λ1≥λ0,one has

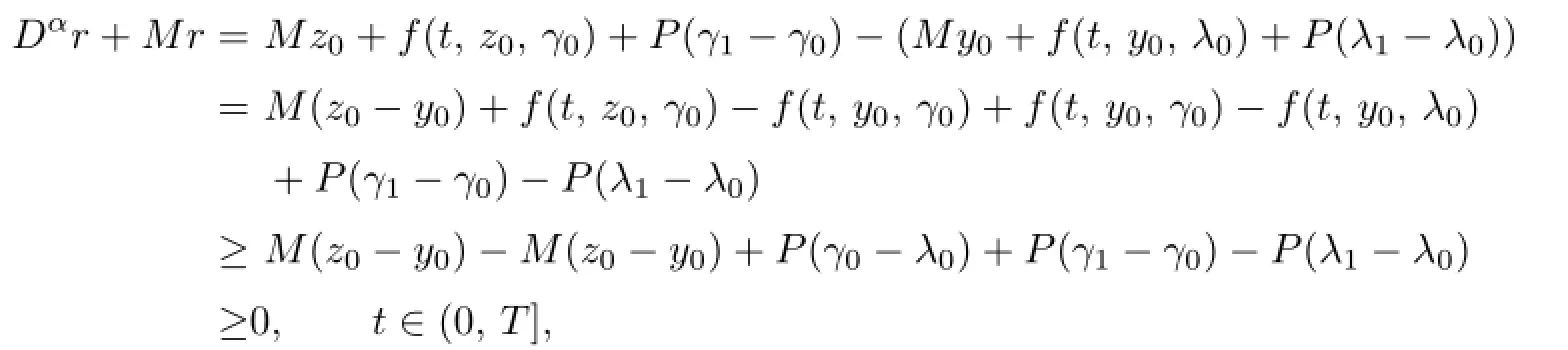
andr(0)=z1(0)−y1(0)=0.

Again,in view of Lemma 2.1,we have

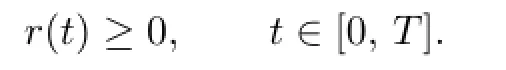
The above conclusion shows that

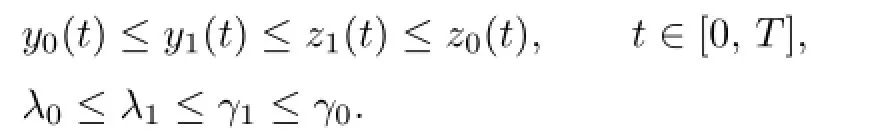
Assume,by induction,

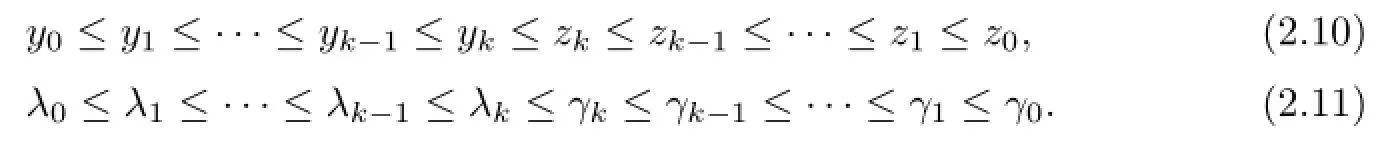
Let

Then by(2.7),λ0≤γ0,5°and(2.11),we have

which implies thath≥0,i.e.,

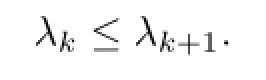
Moreover,by(2.7),2°,3°,h≥0 and(2.10),(2.11),one has

andr(0)=0.

In view of Lemma 2.1,we haver(t)≥0,i.e.,

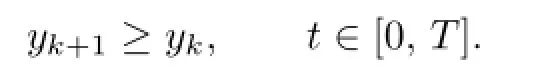
Let

Then,by(2.8),(2.10),(2.11)and 4°,5°,one has

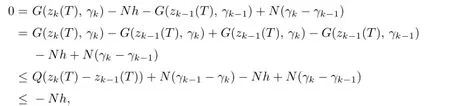
which implies thath≤0,i.e.,

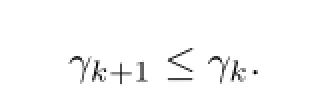
Moreover,by(2.8),h≤0,2°,3°,(2.10)and(2.11),we see thatrsatis fi es

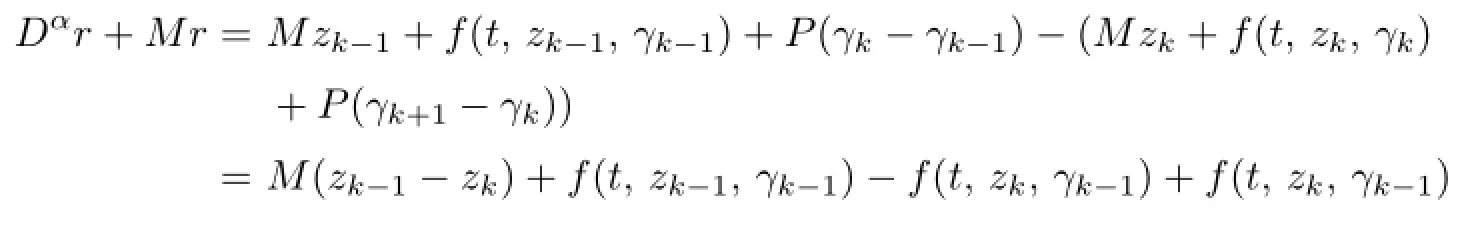
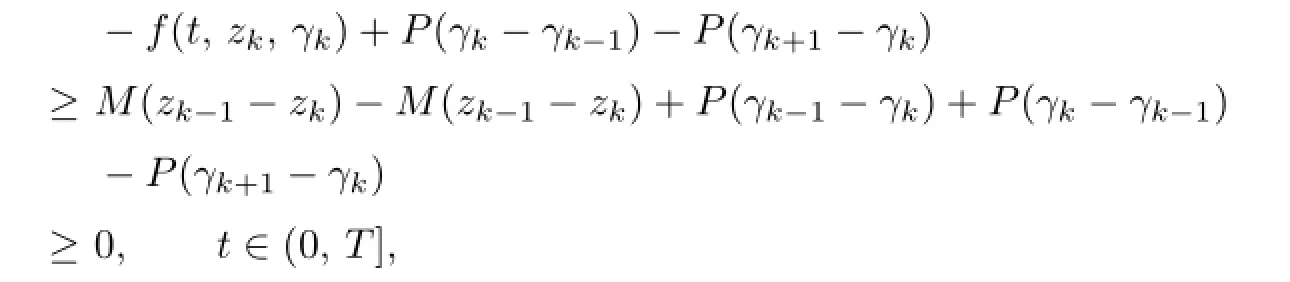
andr(0)=0.

In view of Lemma 2.1,r(t)≥0,i.e.,

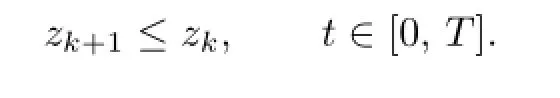
Let

By(2.7),(2.8),(2.10),(2.11)and 4°,5°,one has

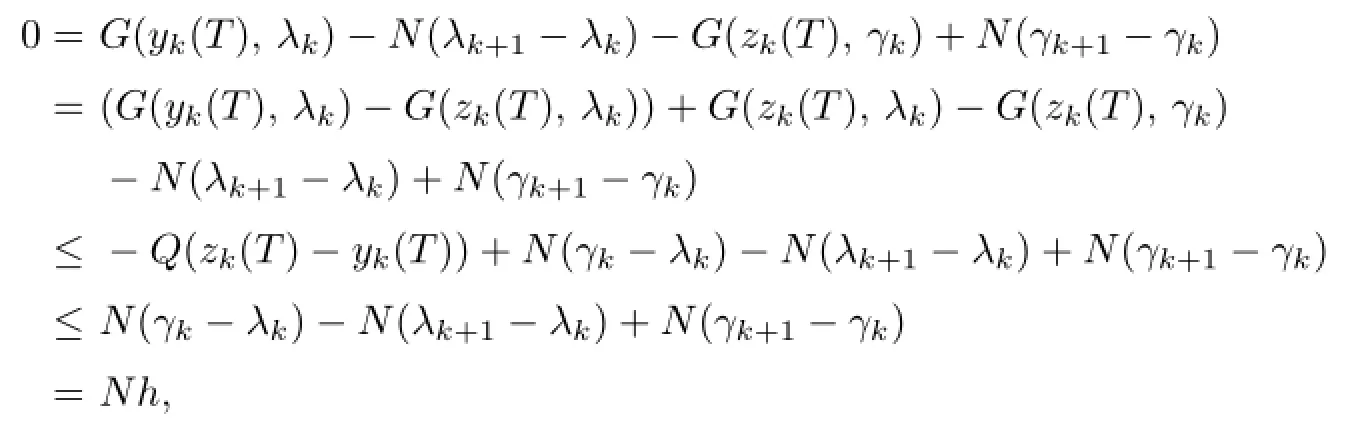
which implies thath≥0,i.e.,

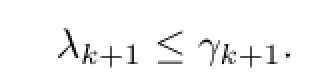
Moreover,by(2.7),(2.8),(2.10),(2.11),h≥0 and 2°,3°,we have

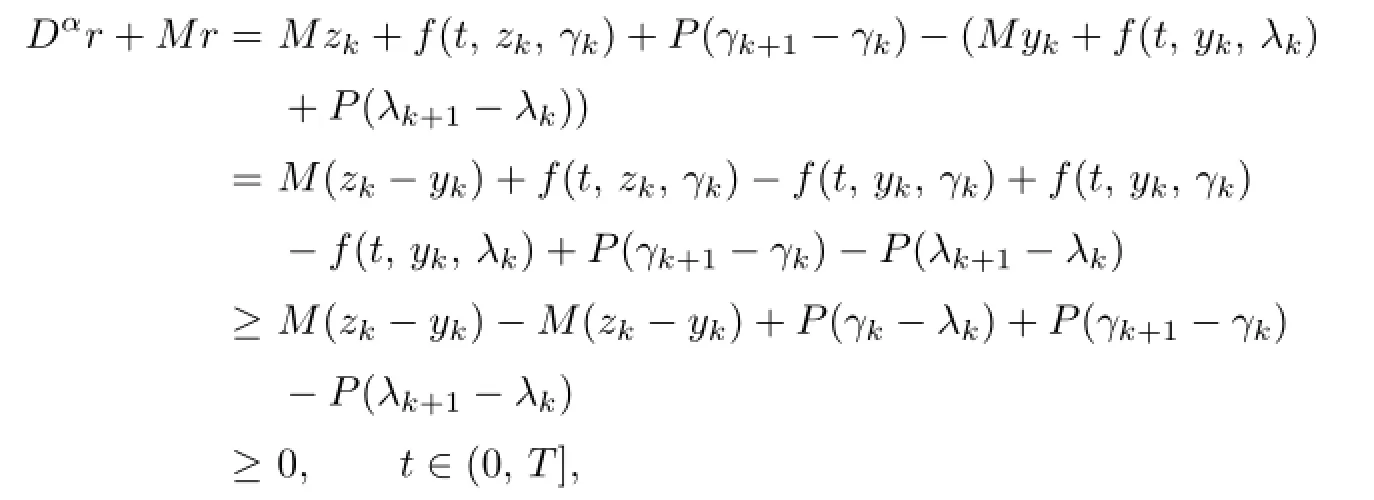
andr(0)=zk(0)−yk(0)=0.

Again,in view of Lemma 2.1,we have

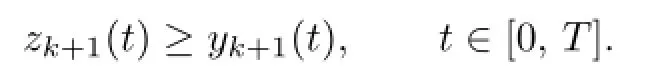
Hence,the monotone property(2.9)follows from the principle of induction.

Step 3.The sequences constructed by(2.7)and(2.8)have pointwise limits and satisfy some relations,that is,

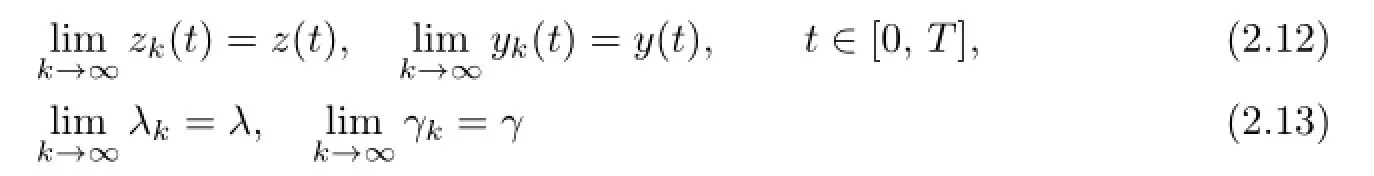
exist and satisfy

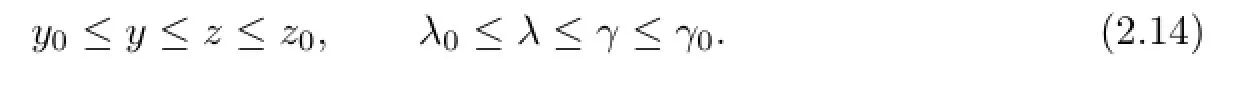
In fact,by(2.8),we see that the sequences{yk}and{λk}are monotone nondecreasing and bounded from above,and the sequences{zk}and{γk}are monotone nonincreasing and bounded from below.Therefore,the pointwise limits exist and these limits are denoted byy,λ,z,γas in(2.12)and(2.13).Moreover,by(2.8),the limitsy,λ,z,γsatisfy(2.14).

Step 4.We prove that the pairs(y,λ)and(z,γ)are the solutions of(1.1).

Let(wk,ρk)be either(yk,λk)or(zk,γk),and

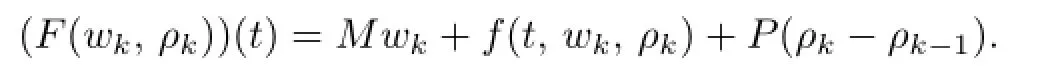
By(1.3),for the linear initial value problem,the solutionwkof(2.7)or(2.8)may be expressed as

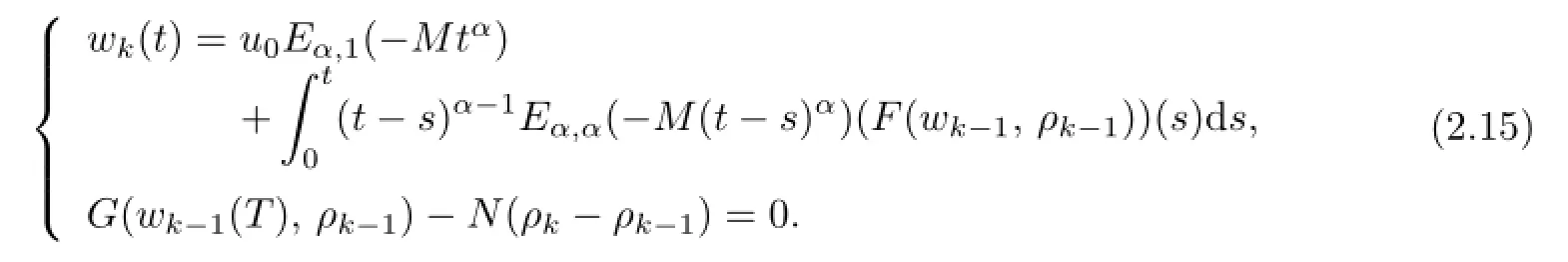
The assumptions of functionf,Gthe monotone convergence ofwktowandρktoρ(see (2.12),(2.13))imply that(F(wk−1,ρk−1))(t)converges to(F(w,ρ))(t),t∈[0,T]andG(w(T),ρ)=0.Letk→∞in(2.15)and by the dominated convergence theorem,wsatis fi es

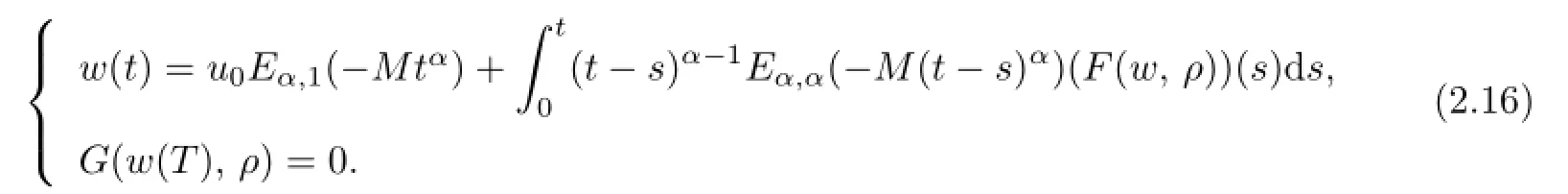
That is,(w(t),ρ)is the representation of the solution of(2.6),that is,(w(t),ρ)is the representation of the solution of(1.1).By the Lemma 1.3 and the continuity assumptions onf,we can easily obtain thatw∈Cα([0,T],R),which proves that the sequences{zk,γk}and{yk,λk}converge to the solutions(z,γ)and(y,λ)of(1.1),and satisfy

Step 5.To complete the proof,we need to show that if(u,β)is any solution of(1.1) such that

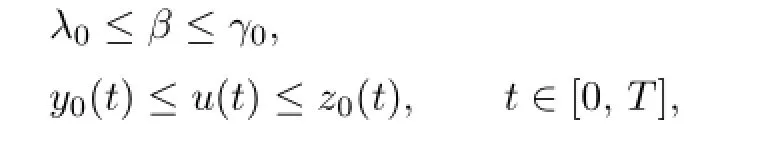
then

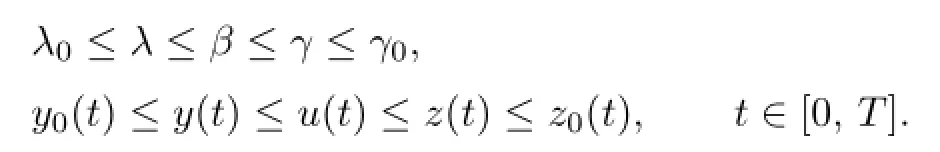
By the analogy arguments as the previous,we can obtain that

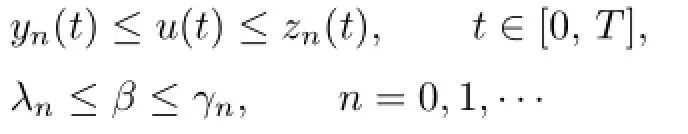
Taking the limits asn→∞,we have

whereyn(t),zn(t),λnandγnare de fi ned by(2.7)and(2.8).It means that(y,λ)and(z,γ) are the minimal and maximal solutions of(1.1),respectively.

3 An Example

In this section,we give an example to illustrate the usefulness of our main result.Let us consider the following fractional di ff erential equation with a parameter:

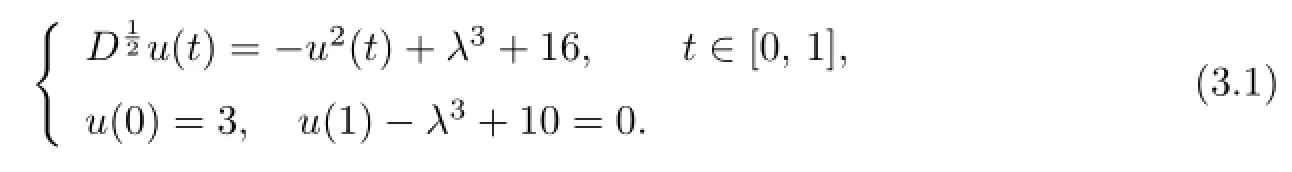
Set

We can verify that(ρ,1)and(12ρ,2ρ)(2＜ρ＜4)are the lower and upper solutions of (3.1),respectively,andf,Gsatisfy assumptions 1°–5°in Theorem 2.1.In fact,

We verify 2°–5°as follows:

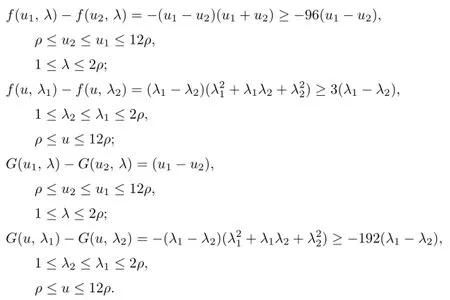
Then,by Theorem 2.1,there exist the monotone sequences{yn,λn},{zn,γn}such that

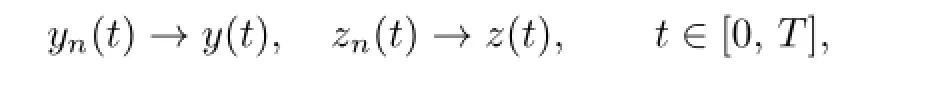
and

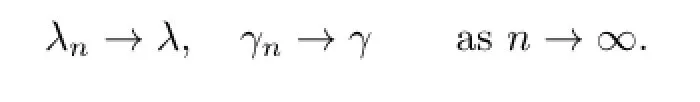
Moreover,(y,λ)and(z,γ)are the minimal and maximal solutions of(3.1),respectively.

[1]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Di ff erential Equations.Amsterdam:Elsevier,2006.

[2]Jankowski T.Convergence of monotone iterations for di ff erential problem.Acta Math.Sinica, 2000,16(4):711–720.

[3]Pitcher E,Sewell W E.Existence theorems for solutions of di ff erential equations of non-integral order,Bull.Amer.Math.Soc.,1938,44(2):100–107.

[4]Al-Bassam M A.Some existence theorems on di ff erential equations of generalized order.J. Reine Angew.Math.,1965,218(1):70–78.

[5]Delbosco D,Rodino L.Existence and uniqueness for a nonlinear fractional di ff erential equation.J.Math.Anal.Appl.,1996,204(2):609–625.

[6]Kilbsa A A,Marzan S A.Nonlinear di ff erential equations in weighted spaces of continuous functions(in Rusian).Dokl.Nats.Akad.Nauk Belarusi,2003,47(1):29–35.

[7]Devi J V,Lakshmikantham V.Nonsmooth analysis and fractional di ff erential equations.Nonlinear Anal.,2009,70:4151–4157.

[8]Kosmatov N.Integral equations and initial value problems for nonlinear di ff erential equations of fractional order.Nonlinear Anal.,2009,70:2521–2529.

[9]Lakshmikantham V,Vatsala A S.Basic theory of fractional di ff erential equations.Nonlinear Anal.,2008,69(8):2677–2682.

[10]Lakshmikantham V,Vatsala A S.General uniqueness and monotone iterative technique for fractional di ff erential equations.Appl.Math.Lett.,2008,21(8):828–834.

[11]McRae F A.Monotone iterative technique and existence results for fractional di ff erential equations.Nonlinear Anal.,2009,71(12):6093–6096.

[12]Zhang S Q.Monotone iterative method for initial value problem involving Riemann-Liouville fractional derivatives.Nonlinear Anal.,2009,71(5/6):2087–2093.

[13]Zhang S Q.Existence of a solution for the fractional di ff erential equation with nonlinear boundary conditions.Comput.Math.Appl.,2011,61(4):1202–1208.

[14]Zhang S Q,Su X W.The existence of a solution for a fractional di ff erential equation with nonlinear boundary conditions considered using upper and lower solutions in reverse order.Comput.Math.Appl.,2011,62(3):1268–1274.

[15]Zhang S Q.Monotone method for initial value problem for fractional di ff usion equation.Sci. China Ser.A,2006,49(9):1223–1230.

tion:26A33,34B15

A

1674-5647(2014)02-0157-11

10.13447/j.1674-5647.2014.02.06

Received date:Dec.15,2011.

Foundation item:The NSF(11371364)of China,the Fundamental Research Funds(2009QS06)for the Central Universities,and the 2013 Science and Technology Research Project(KM201310016001)of Beijing Municipal Education Commission.

*Corresponding author.

E-mail address:shiailing@bucea.edu.cn(Shi A L),zsqjk@163.com(Zhang S Q).