Multilinear Commutators of Sublinear Operators on Triebel-Lizorkin Spaces

SHU LI-SHENG

(1.School of Mathematical Sciences,University of Science and Technology of China, Hefei,230026)

(2.Department of Mathematics,Chaohu University,Chaohu,Anhui,238000)

(3.Department of Mathematics,Anhui Normal University,Wuhu,Anhui,241000)

Multilinear Commutators of Sublinear Operators on Triebel-Lizorkin Spaces

XIE RU-LONG1,2,SHU LI-SHENG3AND ZHANG QIAN-XIANG2,*

(1.School of Mathematical Sciences,University of Science and Technology of China, Hefei,230026)

(2.Department of Mathematics,Chaohu University,Chaohu,Anhui,238000)

(3.Department of Mathematics,Anhui Normal University,Wuhu,Anhui,241000)

Communicated by Ji You-qing

In this paper,the boundedness of multilinear commutators related to sublinear operators with Lipschitz function on Triebel-Lizorkin spaces is given.As an application,we prove that the multilinear commutators of Littlewood-Paley operator and Bochner-Riesz operator are bounded on Triebel-Lizorkin spaces.

multilinear commutator,Triebel-Lizorkin space,Littlewood-Paley operator,Bochner-Riesz operator

1 Introduction

In 2002,P´erez and Trujillo-Gonz´alez[1]introduced a kind of multilinear commutators of singular integral operators withOscexpLr(r≥1)function and obtained sharp weighted estimates for this kind of multilinear commutators.Since then,the properties of multilinear commutators have been widely studied in harmonic analysis(see[1–10]).Huet al.[2], Meng and Yang[3]proved the boundedness of multilinear commutators with non-doubling measures.Chen and Ma[4]established that multilinear commutators related to Calder´on-Zygmund operator and fractional integral operator with Lipschitz function are bounded in Triebel-Lizorkin spaces.Meanwhile,weighted weak-type estimates for multilinear commutators of fractional integrals on homogeneous type spaces were discussed by Gorositoet al.[5]. Later,Mo and Lu[6]studied the boundedness for multilinear commutators of Marcinkiewiczintegral operators on Triebel-Lizorkin spaces and Hardy spaces.Recently,the weighted estimates for multilinear commutators of Littlewood-Paley operators and Marcinkiewicz integrals were established by Xue and Ding[7]and Zhang[8],respectively.The bounded properties for the multilinear commutators ofθ-type Calder´on-Zygmund operators were considered by authors in[9].In 2011,Xieet al.[10]established the endpoint estimate for multilinear commutators of Bochner-Riesz operators.In this paper,the boundedness of multilinear commutators related to sublinear operators on Triebel-Lizorkin spaces is considered.And as an application,we obtain that the multilinear commutators of Littlewood-Paley operator and Bochner-Riesz operator are bounded on Triebel-Lizorkin spaces.

wheredenotes thek-th di ff erence operator(see[11]).

Given any positive integerm,for 1≤i≤m,we denote bythe family of all fi nite subsetsσ={σ(1),σ(2),···,σ(i)}of{1,2,···,m}withidi ff erent elements.For any, the complementary sequencesσ′is given byσ′={1,2,···,m}σ.Letb=(b1,b2,···,bm)be a fi nite family of locally integrable functions.For all 1≤i≤mandσ={σ(1),···,σ(i)we denotebσ=(bσ(1),···,bσ(i))and the productbσ=bσ(1)···bσ(i).Ifβσ(1)+···+βσ(i)=βσ,then we write

For the product of all the functions,we simply write

De fi nition 1.1Let ε＞0and ψ be a fi xed function which satis fi es the following properties:

The multilinear commutators of Littlewood-Paley operator is de fi ned by

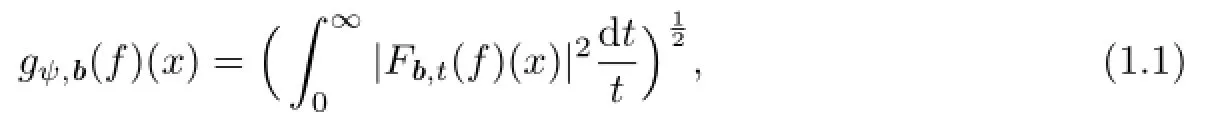
where

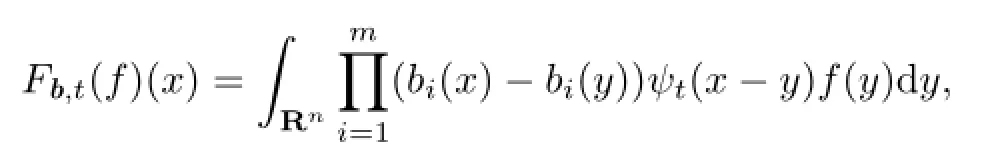
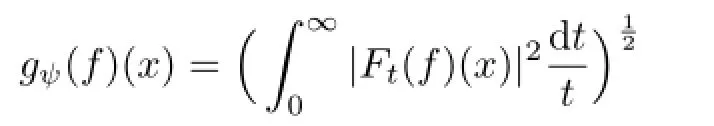
is the Littlewood-Paley g function(see[12]).

LetHbe the space

Then it is clear that

where

The multilinear commutators of Bochner-Riesz operator is de fi ned by

We also de fi ne that

which is the Bochner-Riesz operator(see[13]).

LetHbe the space

Then it is clear that

Generally,we de fi ne the following multilinear commutators related to convolution operators.

De fi nition 1.3Let K(x,t)be de fi ned onRn×[0,+∞),and b=(b1,b2,···,bm)be afi nite family of locally integrable functions with bi∈(Rn),1≤i≤m.Denote

and

LetHbe the space

Then the multilinear commutator is de fi ned by

We also de fi ne that

It is obvious that De fi nitions 1.1 and 1.2 are the particular cases of De fi nition 1.3.Meanwhile,it is pointed out that the multilinear commutators are the generalization of commutator and higher order commutators.In fact,whenm=1,the multilinear commutator is a commutator and whenb1=b2=···=bm,it is a higher order commutator.

2 Main Result and Proof

Now we are going to establish that the multilinear commutators of a sublinear operator are bounded fromLp(Rn)to a Triebel-Lizorkin space by giving a general judgement method.

Theorem 2.1(Main Theorem)Suppose that T,Tbare the same as in De fi nition1.3,where b is as above and such that

Let

where λi=(bi)Q,1≤i≤m.If T is bounded on Lq(Rn)for1＜q＜∞and satis fi es the size condition:

forsuppf⊂(2Q)cand x∈Q=Q(x0,l),then Tbis bounded from Lp(Rn)to(Rn).

To obtain the proof of our main theorem,we need the following lemmas.

Lemma 2.1[11]For0＜β＜1,1＜p＜∞,

Lemma 2.2[11]For0＜β＜1,1≤p＜∞,

For p=∞,the formula should be modi fi ed appropriately.

Lemma 2.4[4]Let f∈Lloc(Rn),1＜r＜∞.Fixed a cube Q and x∈Q,we set f1∈fχ2Q,b=(b1,b2,···,bm)and λ=bQ=(λ1,λ2,···,λm),where λi=(bi)Q,1≤i≤m. Then we have

Proof of Main Theorem For a fi xed cubex∈Q=Q(x0,l)andz∈Q,we obtain

where

For a fi xedf∈Lp(Rn),settingf1=fχ2Q,f2=f−f1,for any real numbera,we get

wherea=a1+a2.

It is easy to see that

Let us estimate II.

For II1,by the H¨older’s inequality,the boundedness ofTand Lemma 2.4,taking 1＜r＜∞,we obtain

For II2,we have

Setting

with the aid of the size condition,we can see that

Therefore,we obtain

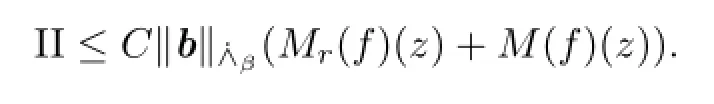
Let us turn to estimate III.

Using the boundedness ofT,the H¨older’s inequality and taking 1＜r＜∞,we deduce that

Setting

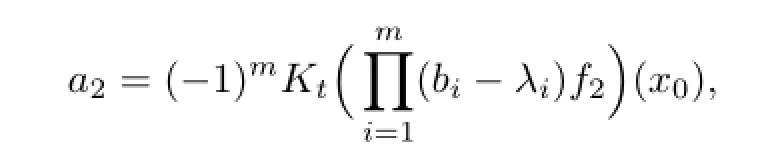
and using the size condition in the main theorem,we see that

Thus

Combining the estimate of I,II and III,we obtain

By Lemma 2.1 and theLp-boundedness ofM,MrandT,we get

Thus the proof of main theorem is completed.

3 Applications

As an application of our main theorem,we obtain in this section that the multilinear commutators of Littlewood-Paley operator and Bochner-Riesz operator are bounded on Triebel-Lizorkin spaces.

Theorem 3.1Suppose that gψ,bis de fi ned by(1.1),where b is as above and such that

Corollary 3.1Suppose that gψ,bis de fi ned by(1.1),where b is as above and such that

To prove the above results,we need the following lemmas.

is bounded from Lp(Rn)to Lq(Rn).

Lemma 3.2Suppose that gψ,bis de fi ned by(1.1),where b is as above and such that

and

Then gψ,bis bounded from Lp(Rn)to Lq(Rn).

Proof.Asbi∈(Rn)(0＜βi＜1)for anyi=1,2,···,m,by the Minkowski’s inequality, one has

Thus we fi nish the proof of Lemma 3.2.

and

Proof of Theorems 3.1 and 3.2 To prove Theorems 3.1 and 3.2,with the help of Lemmas 3.2 and 3.3,it suffices to verify thatgψ,bandsatisfy the size condition in the main theorem.

Suppose thatλ=bQ=(λ1,λ2,···,λm),whereλi=(bi)Q,1≤i≤m,suppf⊂(2Q)cand cubex∈Q=Q(x0,l).

Forgψ,b,since|x0−y|≈|x−y|fory∈(2Q)c,by the Minkowski’s inequality,we obtain

Case 1. 0＜t≤l.

In this case,noticing(see[16])

we have

It follows that

Case 2.t＞l.

We chooseδ0such that

and notice that(see[16])

for anyr=(r1,···,rn)∈(N∪{0})n,where

Therefore

Thus the proofs of Theorems 3.1 and 3.2 are completed.

[1]P´erez C,Trujillo-Gonz´alez R.Sharp weighted estimates for multilinear commutators.J.London Math.Soc.,2002,65:672–692.

[2]Hu G E,Meng Y,Yang D C.Multilinear commutators of singular integrals with non doubling measures.Integral Equations Operator Theory,2005,51:235–255.

[3]Meng Y,Yang D C.Multilinear commutators of Calder´on-Zygmund operators on Hardy-type spaces with non-doubling measures.J.Math.Anal.Appl.,2006,317:228–244.

[4]Chen Y P,Ma B L.The bounedeness of multilinear commutators formLp(Rn)to Triebel-Lizorkin space.Anal.Theory Appl.,2007,23:112–128.

[5]Gorosito O,Pradolini G,Salinas O.Weighted weak-type estimates for multilinear commutators of fractional integrals on spaces of homogeneous type.Acta Math.Sinica,2007,23:1813–1826.

[6]Mo H X,Lu S Z.Boundedness of generalized higher commutators of Marcinkiewicz integrals.Acta Math.Sci.,2007,27B:852–866.

[7]Xue Q Y,Ding Y.Weighted estimates for the multilinear commutators of the Littlewood-Paley operators.Sci.China Ser.A,2009,52:1849–1868.

[8]Zhang P.Weighted estimates for multilinear commutators of Marcinkiewicz integral.Acta Math.Sinica,2008,24:1387–1400.

[9]Xie R L,Shu L S.On multilinear commutators ofθ-type Calder´on-Zygmund operators.Anal. Theory Appl.,2008,24:260–270.

[10]Xie R L,Shu L S,Zhang Q X.Boundedness for multilinear commutators of Bochner-Riesz operator.J.Math.Res.Exposition,2011,31:1074–1080.

[11]Paluszynski M.Characterization of the Besov spaces via the commutator operator of Coifman, Rochberg and Weiss.Indiana Univ.Math.J.,1995,44:1–17.

[12]Torchnisky A.The Real Variable Methods in Harmonic Analysis:Pure and Applied Math. New York:Academic Press,1986.

[13]Hu G E,Lu S Z.The commutator of the Bochner-Riesz operator.Tohoku Math.J.,1996,48: 259–266.

[14]Liu L Z.The continuity of commutators on Triebel-Lizorkin spaces.Integral Equations Operator Theory,2004,49:65–75.

[15]Stein E M.Harmonic Analysis:Real Variable Methods,Orthogonality and Oscillatory Integrals.Princeton:Princeton Univ.Press,1993.

[16]Lu S Z.Four Lectures on RealHpSpaces.River Edge,NJ:World Scienti fi c Publishing,1995.

tion:42B25,42B30

A

1674-5647(2014)02-0168-11

10.13447/j.1674-5647.2014.02.07

Received date:Oct.15,2012.

Foundation item:The Excellent Young Talent Foundation(2013SQRL080ZD)of Anhui Province.

*Corresponding author.

E-mail address:rulongxie@163.com(Xie R L),zhqianxiang@163.com(Zhang Q X).