The Isomorphism Theorem of Regular Bisimple ω2-semigroups

(1.Department of Mathematics,Puer University,Puer,Yunnan,665000)

(2.School of Mathematics,South China Normal University,Guangzhou,510631)

The Isomorphism Theorem of Regular Bisimple ω2-semigroups

SHANG YU1AND WANG LI-MIN2

(1.Department of Mathematics,Puer University,Puer,Yunnan,665000)

(2.School of Mathematics,South China Normal University,Guangzhou,510631)

Communicated by Du Xian-kun

In this paper we study the isomorphisms of two regular bisimpleω2-semigroups and obtain a criterion for two such semigroups to be isomorphic.

regularω2-semigroup,generalized Bruck-Reilly extension,isomorphism

1 Preliminaries

The structure of a bisimpleω-semigroup has been related by Reilly[1].Earlier investigations in[2]we studied regular bisimpleω2-semigroups,characterizing them as the generalized Bruck-Reilly extensions of groups.The results of[2]have generalized the results of regular bisimpleω-semigroups to regular bisimpleω2-semigroups.There is often room for argument as to what constitutes a satisfactory structure theory in the semigroup context.Two questions have traditionally been asked.“Does there exist an associated isomorphism theorem?”and“Does the theory enable one to give an explicit description of the congruences?”The fi rst question is inescapable,and applies in every algebraic context,but for an alleged structure theorem which does not have an associated isomorphism theorem is of little use. Reilly[1]has published these results for isomorphisms from a bisimpleω-semigroup to a bisimpleω-semigroup.In this paper,we give the necessary and sufficient conditions for two regular bisimpleω2-semigroups to be isomorphic.We complete this section with a summary of notions of regular bisimpleω2-semigroups,the details of which can be found in[1–4].

For any semigroupS,we denote byESthe set of idempotents ofS.LetSbe a semigroup such thatESis non-empty.We de fi ne a partial ordering≥onESby the rule thate≥fif and only ifef=f=fe.To avoid ambiguity we sometimes denote a relationKonSbyK(S).Let N0denote the set of all non-negative integers and N denote the set of all positive integers.We de fi ne a partial order on N0×N0in the following manner:if (m,n),(p,q)∈N0×N0,(m,n)≤(p,q)if and only ifm＞porm=pandn≥q.The set N0×N0with the above partial order is called anω2-chain,and is denoted byCω2.Any partially ordered set order isomorphic toCω2is also called anω2-chain.We say that a semigroupSis anω2-semigroup if and only ifESis order isomorphic toCω2.Thus,ifSis anω2-semigroup,then we can write

whereem,n≤ep,qif and only if(m,n)≤(p,q).

Wang and Shang[2]has introduced the generalized Bruck-Reilly extension.Consider a monoidTwithHeas theH-class which contains the identityeofT.Letβ,γbe two homomorphisms fromTintoHe.Letube an element inHeandτube the inner automorphism ofHede fi ned byx→uxu−1such that

We can makeS=N0×N0×T×N0×N0into a semigroup by de fi ning

(m,n,a,q,p)(m′,n′,a′,q′,p′)

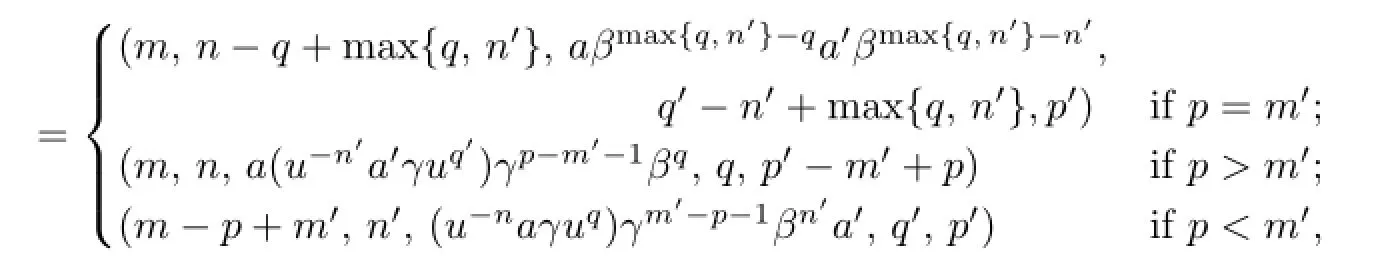
whereβ0,γ0are interpreted as the identity map ofTandu0is interpreted as the identityeofT.ThenSis a semigroup with identity(0,0,e,0,0).The semigroupS=N0×N0×T×N0×N0constructed above is called the generalized Bruck-Reilly extension ofTdetermined byβ,γ,uand is denoted byS=GBR(T;β,γ;u).Let(m,n,a,q,p)∈S.Then(m,n,a,q,p) is an idempotent if and only ifm=p,n=qandais an idempotent.

Lemma 1.1[2]Let S=GBR(T;β,γ;u)be a generalized Bruck-Reilly extension of a monoid T determined by β,γ,u.Suppose that(m,n,a,q,p)and(m′,n′,a′,q′,p′)are elements in S.Then

(i)(m,n,a,q,p)L(S)(m′,n′,a′,q′,p′)if and only if q=q′,p=p′and aL(T)a′;

(ii)(m,n,a,q,p)R(S)(m′,n′,a′,q′,p′)if and only if m=m′,n=n′and aR(T)a′.

Lemma 1.2[2]Let S=GBR(T;β,γ;u).Then an element(m,n,a,q,p)in S has an inverse(x,y,b,z,w)∈S if and only if b is the inverse of a in T,x=p,y=q,z=n and w=m.

Lemma 1.3[2]Let G be a group,β and γ be two endomorphisms of G,and u be an element of G.Let S=GBR(G;β,γ;u)be the generalized Bruck-Reilly extension of G determined by β,γ and u.Then S is a regular bisimple ω2-semigroup.Conversely,every regular bisimple ω2-semigroup is isomorphic to some GBR(G;β,γ;u).

2 The Isomorphism Theorem

In this section,we give the necessary and sufficient conditions for two regular bisimpleω2-semigroups to be isomorphic.LetSandS′be regular bisimpleω2-semigroups.The following theorem is our main result in this paper.

Theorem 2.1Let S=GBR(G;β,γ;u)and S′=GBR(G′;β′,γ′;u′)be two regular bisimple ω2-semigroups.Then S～=S′if and only if there exist an isomorphism α from G to G′and two inner automorphisms τvand τwof G′such that

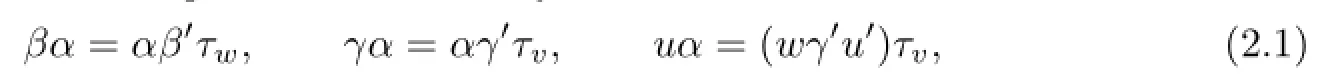
where v and w are two units of G′.

Proof.Letϕbe an isomorphism fromStoS′.Thenϕmust induce a one-to-one order preserving mapping fromEStoES′.Thus(m,n,e,n,m)ϕ=(m,n,e′,n,m),for allmandnin N0,whereeande′are identities ofGandG′,respectively.For any elementa=(m,n,x,q,p)ofS,letaϕ=(m,n,x,q,p)ϕ=(i,j,y,l,k)=b.Now,a−1ϕ=(aϕ)−1,and so

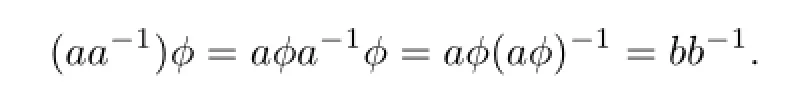
Thus,(m,n,e,n,m)ϕ=(i,j,e′,j,i).Hencem=iandn=j.Similarly,q=landp=k.Thus,for any element(m,n,x,q,p)ofSwe have(m,n,x,q,p)ϕ=(m,n,y,q,p),for some elementyofG′.

We de fi ne a mappingαfromGtoG′such that(0,0,g,0,0)ϕ=(0,0,gα,0,0).Sinceϕis an isomorphism and send the unit group ofSonto the unit group ofS′,it follows thatαis a bijection.It is straightforward to verify thatαis also a homomorphism.Now suppose that(0,0,e,0,1)ϕ=(0,0,v,0,1)and(0,0,e,1,0)ϕ=(0,0,w,1,0),for somew∈G′andv∈G′.Then,for allxinG,

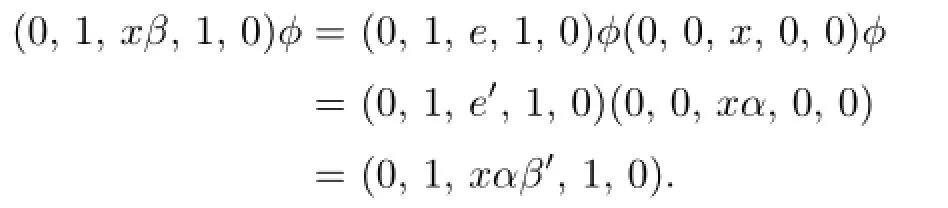
Also

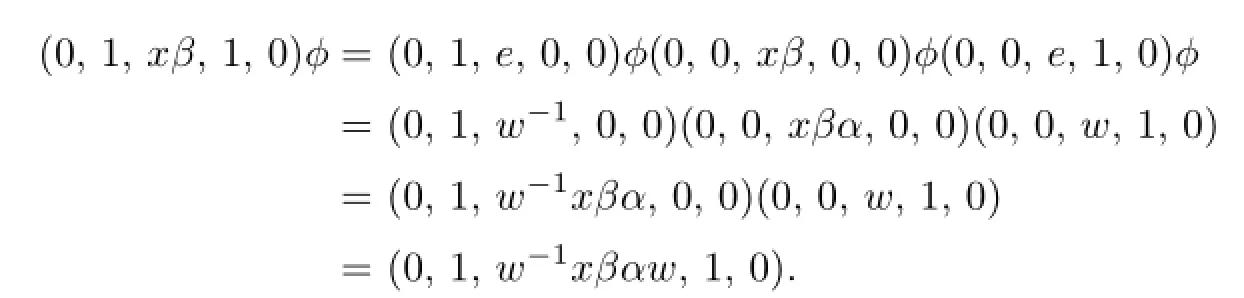
Hence,for all elementsxofG,we havexαβ′=w−1xβαw,that is,xαβ′τw=wxαβ′w−1=xβα.Thus,βα=

For allxinG,

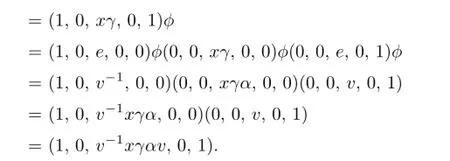
Hence,for all elementsxofG,we havexαγ′=v−1xγαv,that is,xαγ′τv=vxαγ′v−1=xγα.

Thusγα=

Since

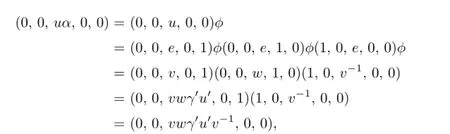
it is clear thatuα=(wγ′u′)τv.

Conversely,suppose that there exists an isomorphismαfromGtoG′such thatβα==αγ′τvanduα=(wγ′u′)τvfor somewofG′and somevofG′.

For each positive integerm,letwm=w(wβ′)···(wβ′m−1)andvm=v(vγ′)···(vγ′m−1).

Then=(w−1β′m−1)···(w−1β′)w−1andvm−1=(v−1γ′m−1)···(v−1γ′)v−1.Letw0=v0=e′.Note thatw1=wandv1=v.We claim that

wherei∈N0.Clearly,this is true fori=0.Suppose that it is true fori=m,and letx∈G′.Then

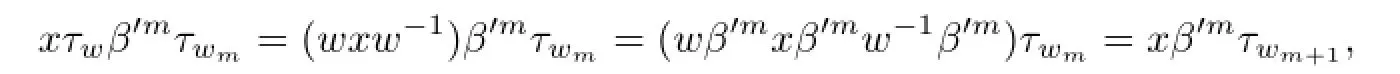
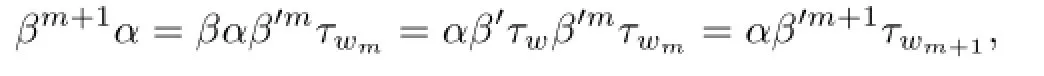
so(2.2)holds by induction.Similarly,we have that

We note that

Clearly,this is true forr=0.Assume that it holds forr=n.Then,by(1.1),we haveγ′τu′=β′γ′,and sou′nwγ′=u′n−1wβ′γ′u′=u′n−2wβ′2γ′u′2=···=wβ′nγ′u′nand

Hence the result holds forr=n+1 and so,by induction,it holds for all non-negativer.

Writeh=(0,0,w,1,0).Sincewis an element inG′,(0,0,w,1,0)and(0,1,w−1,0,0) must be mutually inverse regular elements ofS′,and soh−1=(0,1,w−1,0,0).Letk=(0,0,v,0,1).Similarly,(0,0,v,0,1)and(1,0,v−1,0,0)must be mutually inverse regular elements ofS′,and sok−1=(1,0,v−1,0,0).Writeh0=(0,0,e′,0,0)andk0=(0,0,e′,0,0).A straightforward calculation shows that

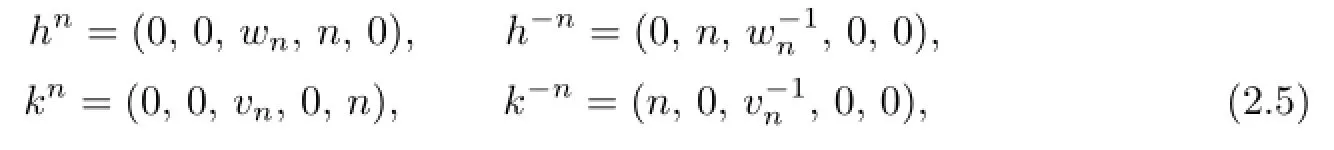
for all non-negative integersn.

Letσbe a mapping fromStoS′,de fi ned by

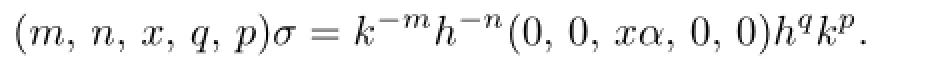
Thus,applying(2.5),we see that

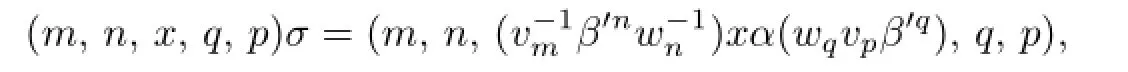
soσis a bijection.

Let(m,n,x,q,p),(m′,n′,x′,q′,p′)∈S.We show that

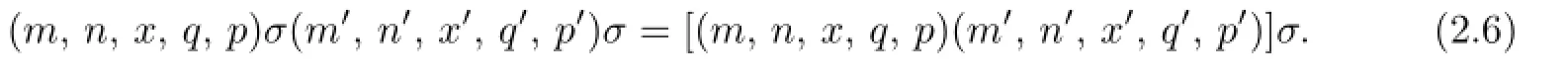
It is convenient to consider separately the following fi ve cases.

Case I.p=m′andq=n′.We have

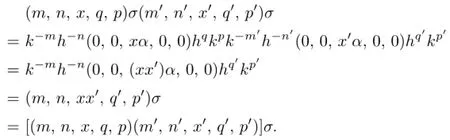
Case II.p=m′andq＞n′.By(2.2),we have

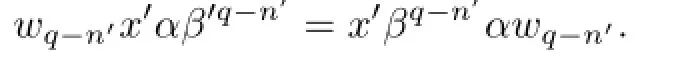
Thus,using(2.5),we obtain

Case III.p=m′andq＜n′.By(2.2),we have

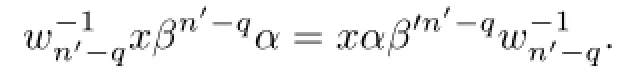
Thus,using(2.5),we obtain

Case IV.p＞m′.Utilizing(2.2)–(2.4),we easily see that

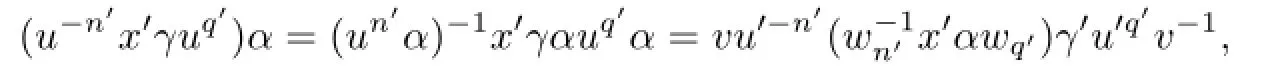
and so

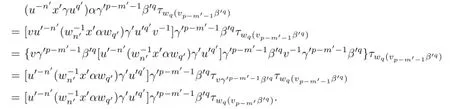
By virtue of(2.2)–(2.4)we have

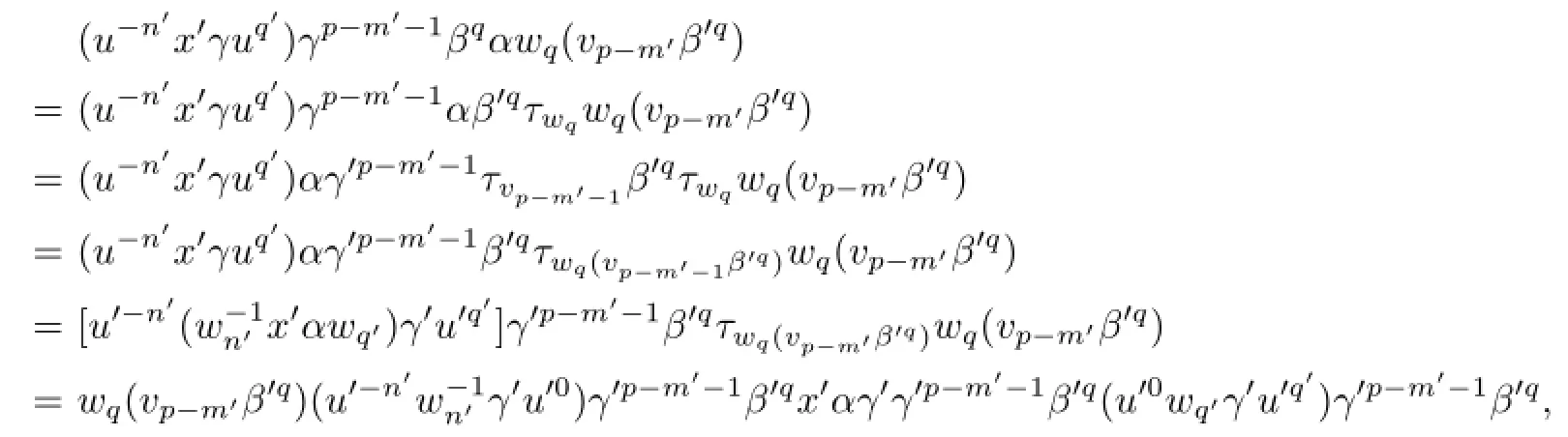
and so

Thus,by(2.5),we obtain

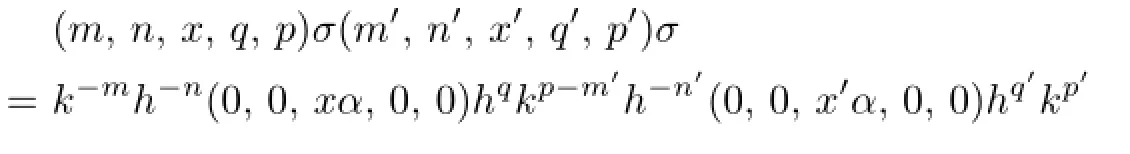
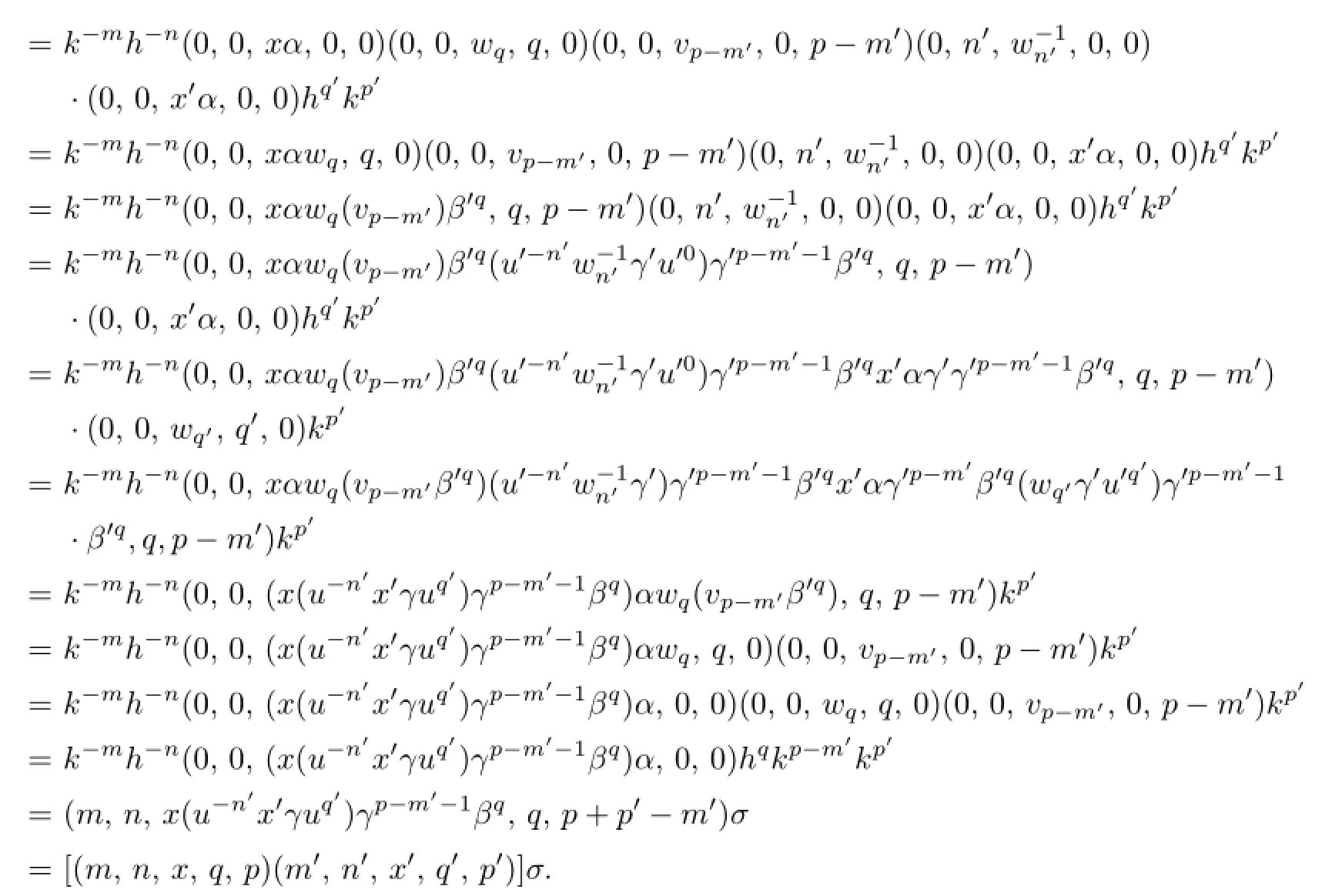
Case V.p＜m′.Utilizing(2.2)–(2.4),we easily see that

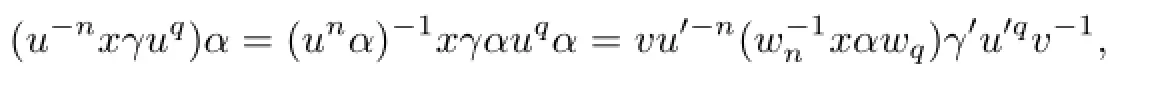
and so

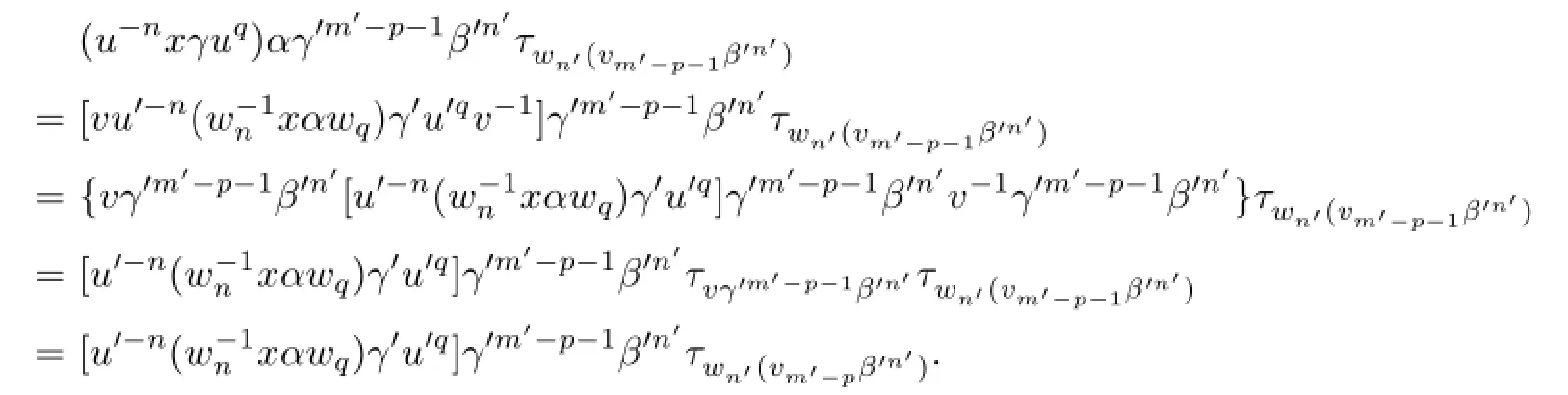
By virtue of(2.2)–(2.4),we have

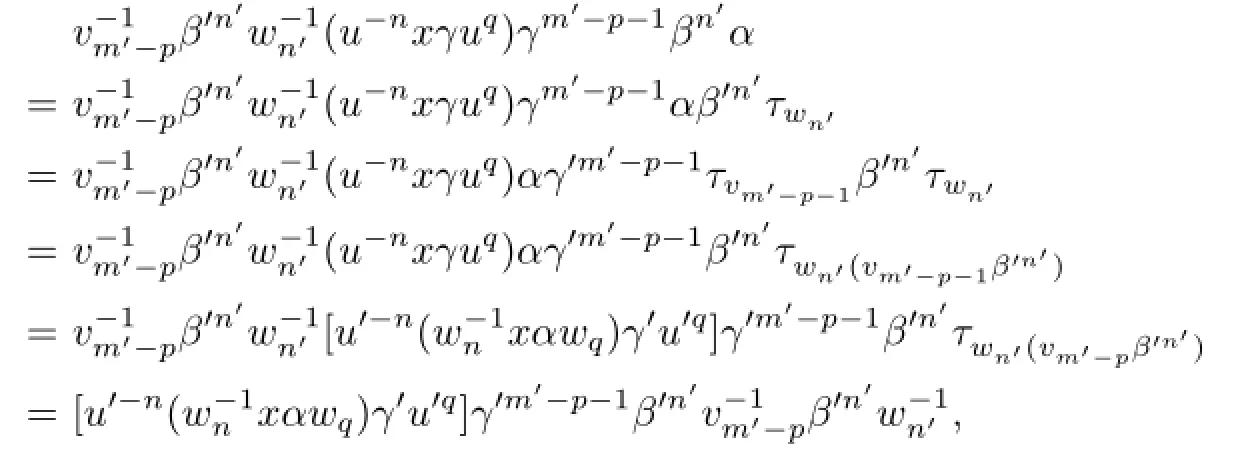
and so

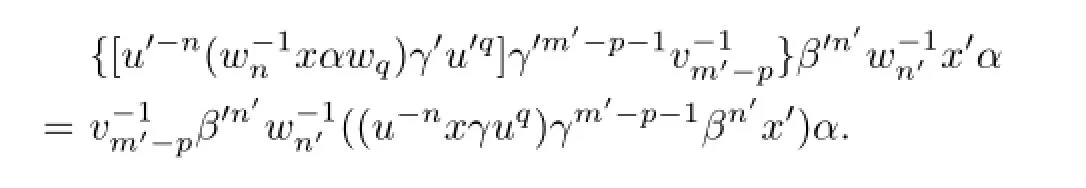
Thus,by(2.5),we obtain

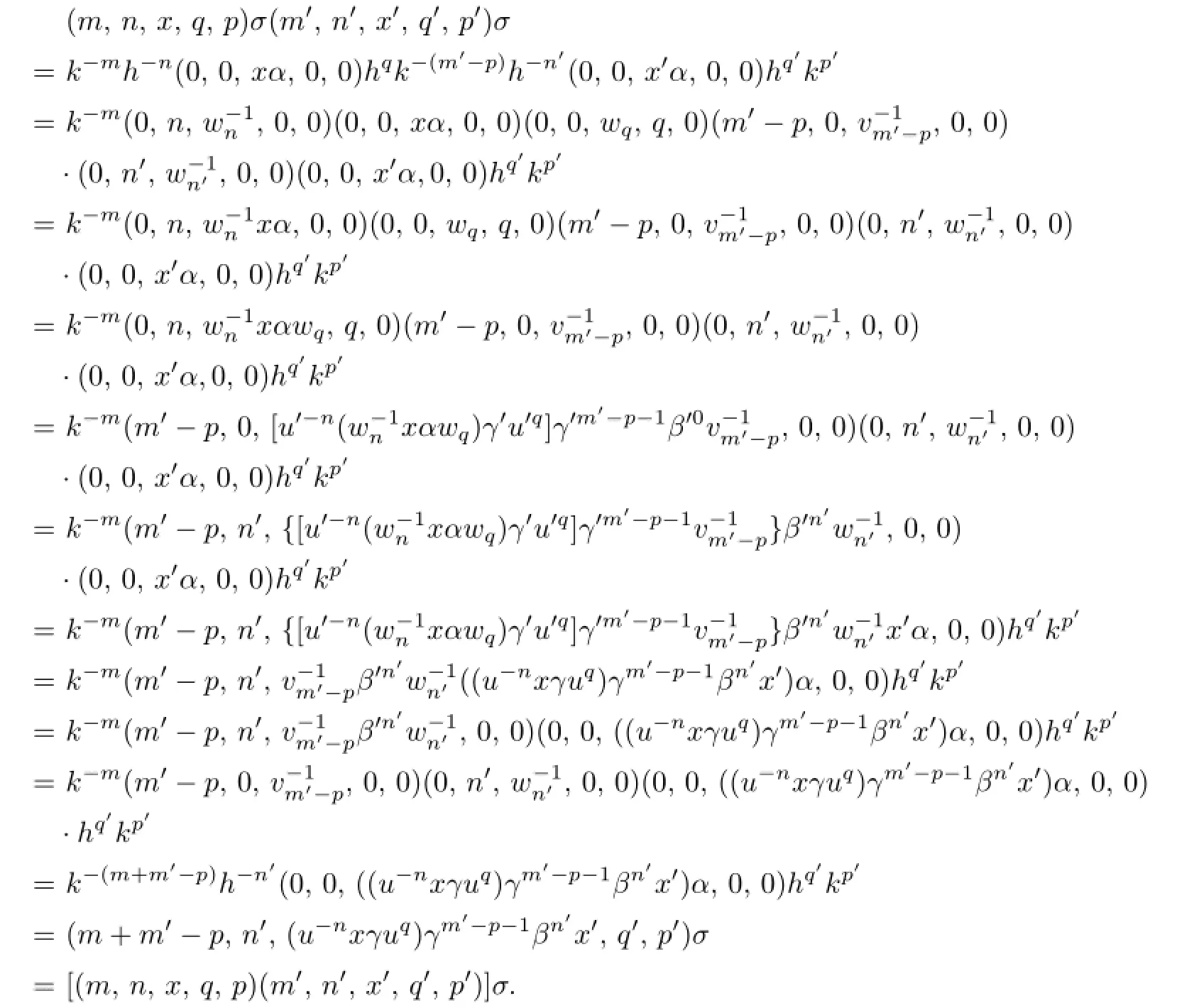
This completes the proof.

[1]Reilly N R.Bisimpleω-semigroups.Proc.Glasgow Math.Assoc.,1966,7:160–167.

[2]Wang L M,Shang Y.Regular bisimpleω2-semigroups.Adv.in Math.(China),2008,37(1): 121–122.

[3]Munn W D.Regularω-semigroups.Glasgow Math.J.,1968,9:46–66.

[4]Howie J M.Fundamentals of Semigroup Theory.Oxford:Clarendon Press,1995.

tion:20M10

A

1674-5647(2014)02-0131-08

10.13447/j.1674-5647.2014.02.04

Received date:Aug.18,2012.

Foundation item:The NSF(10901134)of China and the Science Foundation(2011Y478)of the Department of Education of Yunnan Province.

E-mail address:shangyu503@163.com(Shang Y).