相位正弦扰动的孤岛检测新方法

何 宇，魏艳君，罗 琦，丁 浩

（1.燕山大学电气工程学院，秦皇岛066004；2.南京信息工程大学信息与控制学院，南京210044）

光伏逆变器接入电网必须要考虑到孤岛的发生[1]。所谓孤岛现象是指大电网由于某种原因停止供电后，各接入电网的分布式发电系统未能及时检测出停电而仍然持续向负载供电，从而与负载形成一个电力系统无法控制的独立供电系统[2]。一旦孤岛发生，将会对维修人员及用户端的设备造成严重危害[3-4]。因此，光伏系统必须要具备快速有效的孤岛检测手段，从而进行相应的孤岛保护。

孤岛检测方法可以分为被动法和主动法[5]。被动检测法是通过测得公共耦合点PCC（point of common coupling）的电压参数，包括幅值、频率、相位和谐波等，来判断孤岛的发生，当参数波动超过所设阈值时，逆变器自动做出孤岛保护。被动法的优点是工作原理简单，对电能质量无影响；缺点是当逆变器的输出功率与本地负载吸收的功率相平衡时无法检测出孤岛效应，即该法存在较大的孤岛检测盲区NDZ（non-detection zone）[6]。主动检测法是通过有源扰动或正反馈引发系统偏离正常稳定工作点来实现孤岛检测，其扰动量包括输出电流的幅值、频率、相位及谐波和输出有功/无功功率等。主动法的优点是检测精度高，检测盲区小；缺点是引入的电流扰动会对电能质量带来负面影响[7-8]。

常见的主动式孤岛检测方法有主动频率偏移法[9]、滑模频率偏移法[10]、自动相位偏移法[11]和有功/无功扰动法[12-13]。这些方法虽然可以提高孤岛的检出率，但并不能真正消除检测盲区，或在消除原有检测盲区的同时会带来新的检测盲区。

针对上述不足，本文提出了相位正弦扰动的主动式孤岛检测方法。仿真表明该方法不影响并网电流的形状（过零点、幅值和基波），提高了逆变器的输出功率因数，且不存在检测盲区。

1 相位正弦扰动的检测方法

1.1 检测原理

假若三相光伏系统中未加入孤岛检测环节，由于光伏逆变器是单位功率因数输出，故光伏系统稳定时的输出电流为

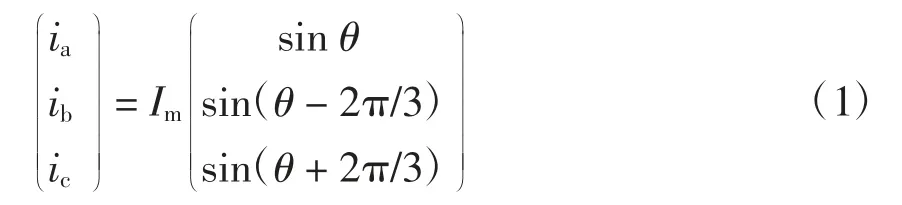
式中，Im和θ 分别为输出电流的幅值和a 相相位。

相位正弦扰动法就是通过改变指令电流，在输出电流的相位中加入微弱的正弦扰动，即期望输出电流稳定时为

式中，k 为所加正弦扰动的强度。

相位中加入正弦扰动并不影响输出电流的过零点和幅值。不影响幅值是显然的，对于过零点，可做以下简要论证。

未对相位做正弦扰动时，由式（1）知a 相输出电流的过零点为

将式（3）代入式（2）的a 相输出电流可得

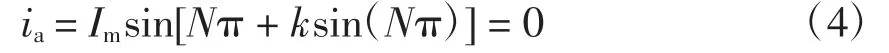
从式（4）可以看出，a 相输出电流的过零点未发生变化，其余两相亦是如此。

图1 和图2 分别显示了k = 0.02 和k = 0.20时a 相输出电流的波形。

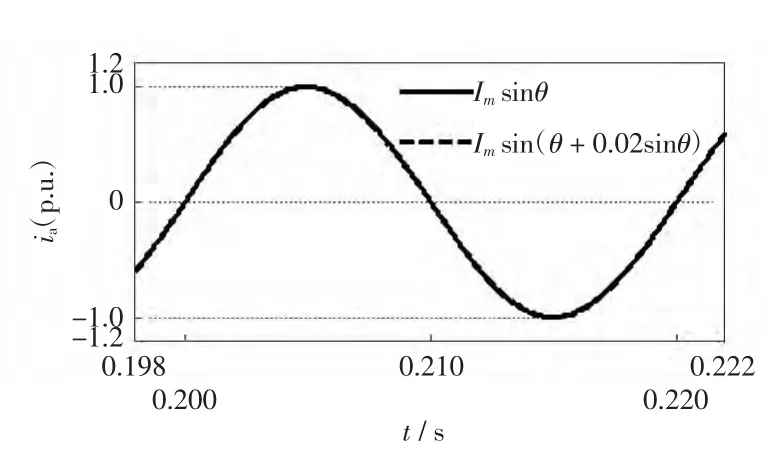
图1 k=0.02 时的a 相输出电流Fig.1 Phase-a output current with k=0.02

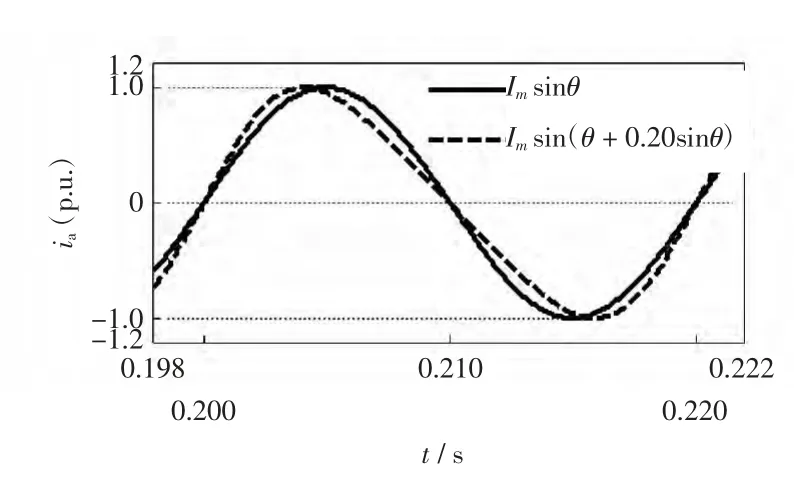
图2 k=0.20 时的a 相输出电流Fig.2 Phase-a output current with k=0.20

由图1 和图2 可看到，输出电流的过零点和幅值与所加正弦扰动的强度k 无关，但k 的大小会对输出电流的畸变程度产生影响：k 越大，输出电流的畸变越大；反之则越小。一般取k≤0.02。

由三角函数知识可知

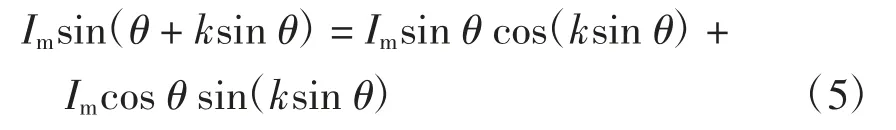
当k→0 时，ksin θ→0，于是有

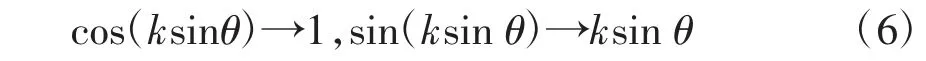
将式（6）代入式（5）可得

由式（7）可知，在输出电流的相位中加入正弦扰动ksin θ 相当于在输出电流中引入了幅值为0.5 kIm的二次谐波，选择式（7）的左式是因为其不影响输出电流的幅值，而右式会加大输出电流的幅值。另外，由式（7）还可看到，加入相位正弦扰动后，输出电流的基波仍为Imsin θ，与电网电压依旧同频同相，保证了光伏逆变器的单位功率因数输出。

以上讨论的对象是a 相输出电流，对于b、c 两相可做同样的分析。

图3 为孤岛检测电路原理。其中，光伏逆变器的输出端与电网连接于PCC，负载采用RLC 并联形式，通过开关S 的打开来模拟孤岛的发生。

如图3 所示，三相光伏逆变器并网运行时，PCC 电压受电网电压钳制而保持不变，理想情况下为

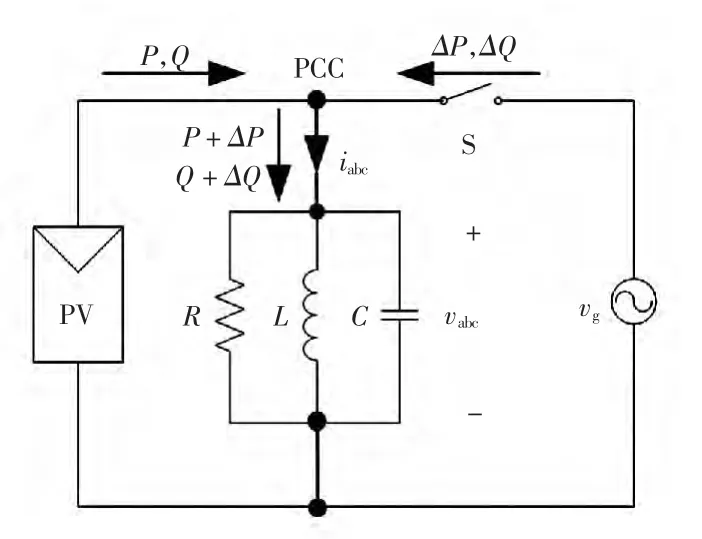
图3 孤岛检测原理Fig.3 Schematic diagram of islanding detection

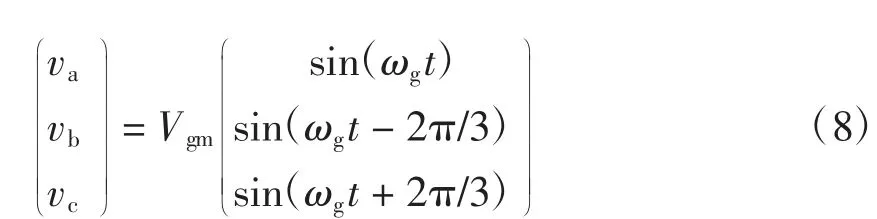
式中，Vgm和ωg分别为电网电压的幅值和角频率，此时PCC 电压的dq 轴分量为

当电网断电，孤岛发生后，PCC 电压将由逆变器的输出电流和本地负载共同决定，其值为

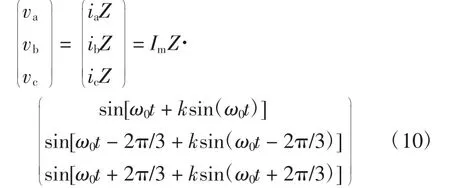
式中：Z 为负载阻抗；ω0为输出电流的基波角频率。

由式（7）可知当k≈0 时，有

将式（11）代入式（10）得

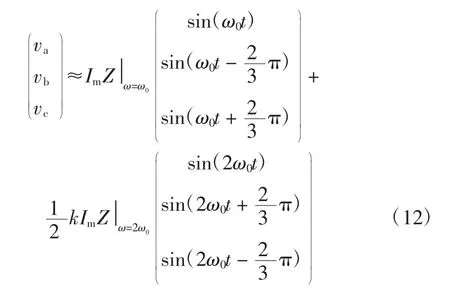
因为负载采用RLC 并联形式，故有

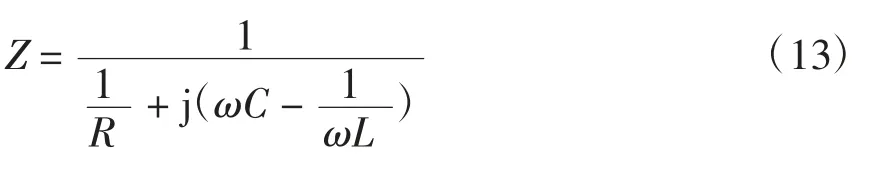
由于光伏系统内部锁相环PLL（phase locked loop）的不断调整，最终会使得PCC 电压的基波和输出电流的基波同频同相，故稳定时PCC 电压的基波角频率和输出电流的基波角频率都为负载的谐振角频率，即

当输出电流的基波流经负载时，由式（13）有

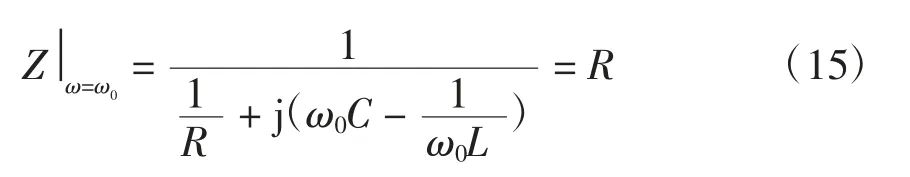
当输出电流的二次谐波流经负载时，由式（13）有

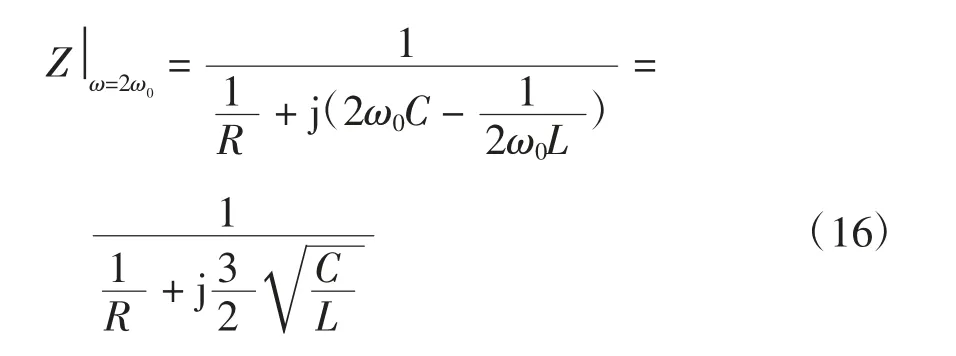
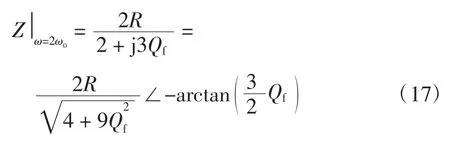
将式（15）和式（17）代入式（12）可得（令Vm=ImR）

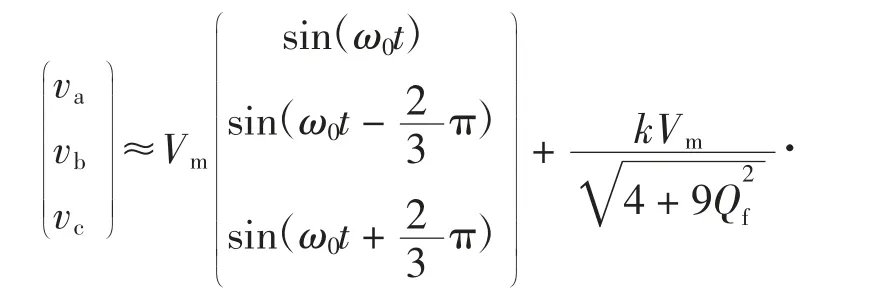
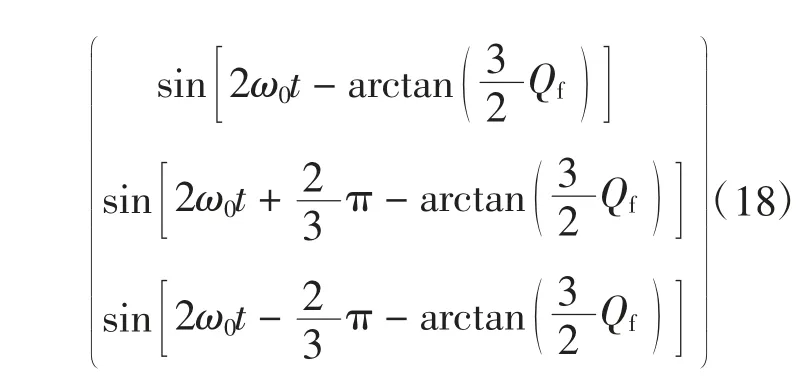
对式（18）作abc-dq 变换得

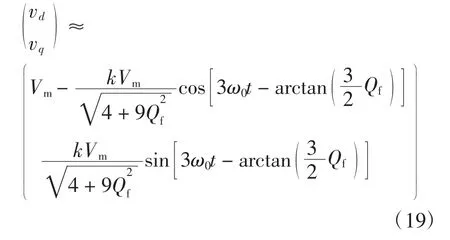
由式（9）和（19）可看到，光伏逆变器并网运行时，vq的幅值为0；光伏逆变器孤岛运行时，vq的幅值近似为因此可通过检测vq的幅值来判断孤岛的发生。为得到检测孤岛的定量条件，还需对vq的幅值做进一步的量化处理。

1.2 孤岛检测出的量化分析

记Vqm为vq的幅值，定义孤岛检测度为

当光伏逆变器并网运行时，由式（9）可知vq=0，Vqm=0，则

当光伏逆变器孤岛运行时，由式（19）可得Vqm≈于是

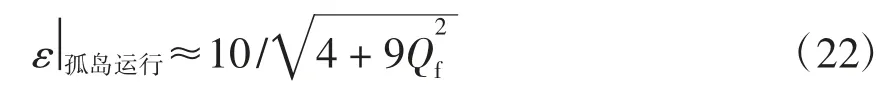
目前绝大多数孤岛测试的标准中Qf≤2.5，在IEEE Std.929—2000 标准[2]中Qf的推荐测试值为2.5。因此，本文考虑Qf=2.5 的最恶劣情况，于是式（22）变为

由式（21）和式（23）可以看到，孤岛前后检测度ε 的值由0 变到了1.29（当Qf小于2.5 时，这个值将更大）。因此，可以根据ε 的值来判断孤岛的发生，为留有一定的裕量，当检测到ε 大于1（这个值记为检测度阈值）时，则孤岛可能已发生。这里还不能肯定孤岛一定发生，因为还要考虑到：①电网电压瞬间的较大波动可能会导致光伏逆变器并网时就有ε 大于1；②式（23）是光伏系统在孤岛运行时稳定后得到的结果，在稳定前ε 的值也有可能大于1。为了避免误动作，可预先设定一时间阈值，当ε 持续大于1 的时间累计达到时间阈值时，则说明孤岛已经发生，可做出孤岛保护。

于是问题就转换为如何求取孤岛检测度ε，由ε 的定义可知，要测得ε 就要求得两个量：vq的幅值Vqm和PCC 电压的基波幅值Vm。Vm可利用图4所示的三相锁相环[14]PLL 测量PCC 电压得到（此锁相环不需另外设计，因为光伏系统本身就需要该锁相环来提供相位）。Vqm的求得方法与求取Fourier系数的方法类似，具体如下。

由式（19）可知vq= Vqmsin[3ω0t - arctan（3Qf/2）]，令uα=sin（3ω0t），uβ=cos（3ω0t），T=2π/（3ω0）。t0表示任一时刻。于是有

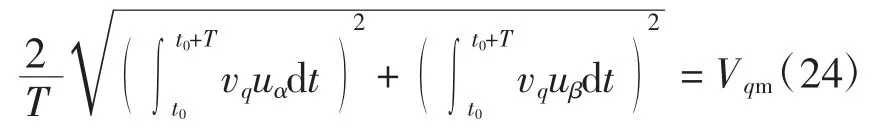
因此，可利用式（24）的左式来获取vq的幅值Vqm。uα、uβ和T 中的ω0即为PCC 电压的基波角频率，可由图4 所示的锁相环提取。

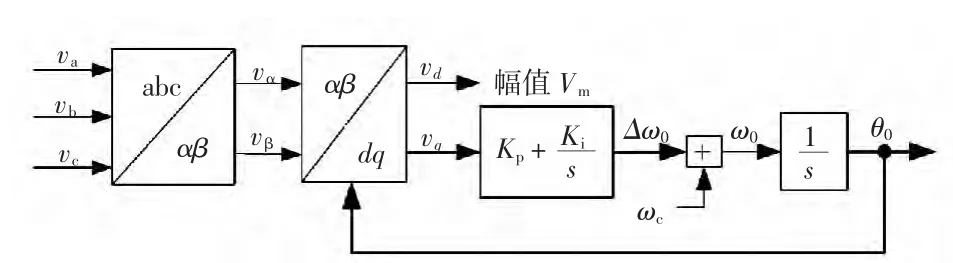
图4 三相锁相环的基本结构Fig.4 Basic structure of three-phase phase-locked loop

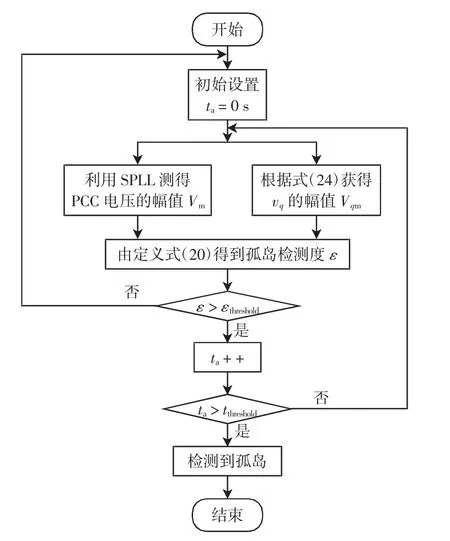
图5 孤岛检测流程Fig.5 Flow chart of islanding detection

综上所述，图5 显示了该孤岛检测方法的流程。（图中SPLL 是软件锁相环（software phase locked loop）的简称，εthreshold和tthreshold分别表示检测度阈值和时间阈值）

另外要说明的是，在负载平衡的条件下，不管负载情况如何，只要孤岛发生，孤岛检测度ε 的值必然发生变化，孤岛必能检测出，故该孤岛检测法不存在检测盲区。

2 仿真验证

IEEE Std.929—2000 标准定义了孤岛检测的最恶劣情况，采用Matlab/Simulink 对此进行相位正弦扰动的仿真验证。具体参数设置如下：三相电网电压的规格为380 V/50 Hz；直流母线电压为800 V；并网滤波电感为6 mH；开关频率为20 kHz；光伏逆变器额定功率为9 kW，单位功率因数输出；并联RLC 负载的有功功率与逆变器相匹配，负载品质因数为2.5、谐振频率为50 Hz，具体各参数为：R=16.13 Ω、L=20.54 mH、C=493.25 μF；相位中所加正弦扰动的强度k=0.02；检测度阈值设为1，时间阈值设为0.2 s（选取阈值时既要满足IEEE Std.929—2000 的相关标准，又要不影响检测的快速性，故折衷选了此值）。仿真时设置三相光伏逆变器在0.1 s 时脱离电网，仿真结果如图6 所示。

由图6（a）～（c）可看到，由于0.1 s 前逆变器处于并网运行，PCC 电压受电网电压钳制而保持平衡，vq为0，孤岛检测度ε=0。在0.1 s 断网后，PCC电压将由逆变器的输出电流和本地负载共同决定，由于相位的正弦扰动，vq不再为0，开始做正弦振荡，稳定时其幅值约为0.8 V，频率为150 Hz，是负载谐振频率的3 倍，符合式（19），ε 的值最终在1.25 附近徘徊，与推出的式（23）相近。

由图6（c）～（e）可看到，在0.106 3 s 后ε 的值恒大于1，到0.306 3 s 时ε 持续大于1 的时间达时间阈值0.2 s，此时逆变器的输出电流突降为0，逆变器停止工作，PCC 电压此后不断减小，直至为0，从而实现了孤岛保护。

由图6（f）可看到，并网时光伏逆变器输出电流的THD 值为1.5%，低于并网标准规定的5%；由图6（g）可看到，逆变器并网时的输出电流和电网电压同频同相，仍是单位功率因数输出。从这两方面可说明，相位正弦扰动法对电能质量的影响非常小。

检测时长为（0.306 3- 0.1）s=0.206 3 s，远低于IEEE Std.929—2000 标准规定的2 s，满足孤岛检测要求。

图6 仿真结果Fig.6 Simulation results

3 结语

本文提出了一种新型的主动式孤岛检测方法——相位正弦扰动法，即对输出电流的相位进行微弱的正弦扰动，使得PCC 电压的q 轴分量在孤岛产生后发生了明显变化。通过对该分量的幅值做进一步的量化处理，得到了检测出孤岛的定量条件：即孤岛前后定义的孤岛检测度ε 的值由0变化到1.29。该检测方法不影响逆变器输出电流的过零点、幅值和基波，过零点和幅值不变化说明了对输出电流所造成的畸变很小，基波不变化保证了光伏逆变器的单位功率因数输出。另外，不管负载情况如何，只要负载平衡，一旦孤岛发生，PCC电压q 轴分量的幅值必然发生变化，从而检测出孤岛，所以这种方法不存在检测盲区。此外，本文还给出三相对称正弦电压和单相正弦电压幅值的提取方法。最后对IEEE Std.929—2000 标准中定义的最恶劣情况进行了仿真验证，结果表明提出的检测方法可实现快速有效的孤岛检测，并对电能质量的影响很小。

文中推出的结论是在三相负载平衡的条件下获得的，然而在实际应用中却存在三相负载不平衡的情况，故本文在这方面可做进一步探讨。

[1]Smith G A，Onions P A，Infield D G. Predicting islanding operation of grid connected PV inverters[J].IEE Proceedings-Electric Power Applications，2000，147（1）：1-6.

[2]IEEE Std 929—2000，IEEE recommended practice for utility interface of photovoltaic（PV）systems[S].

[3]龚会茹，易灵芝，沈建飞，等（Gong Huiru，Yi Lingzhi，Shen Jianfei，et al）.光伏并网系统中的新型孤岛检测方法（New island detection method of PV grid-connected system）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（1）：59-65.

[4]Massoud A M，Ahmed K H，Finney S J，et al. Harmonic distortion-based island detection technique for inverterbased distributed generation [J]. IET Renewable Power Generation，2009，3（4）：493-507.

[5]Teodorescu R，Liserre M，Rodríguez P.Grid Converters for Photovoltaic and Wind Power Systems[M]. Hoboken：John Wiley&Sons，2011.

[6]Ciobotaru M，Agelidis V，Teodorescu R.Accurate and lessdisturbing active anti-islanding method based on PLL for grid-connected PV inverters[C]//IEEE Power Electronics Specialists Conference.Rhodes.Greece：2008.

[7]郭小强，邬伟扬（Guo Xiaoqiang，Wu Weiyang）. 微电网非破坏性无盲区孤岛检测技术（Non-devastating islanding detection for microgrids without non-detection zone）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（25）：7-12.

[8]周诗嘉，陆格文，黎涛，等（Zhou Shijia，Lu Gewen，Li Tao，et al）. 自适应主动频率偏移孤岛检测新方法（Adaptive active frequency shift islanding detecting new method for grid-connected inverters）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：78-82.

[9]Lopes L A C，Huili Sun. Performance assessment of active frequency drifting islanding detection methods [J]. IEEE Trans on Energy Conversion，2006，21（1）：171-180.

[10]Singam B，Hui L Y. Assessing SMS and PJD schemes of anti-islanding with varying quality factor [C]//IEEE International Power and Energy Conference. Putra Jaya，Malaysia：2006.

[11]Guo-Kiang Hung，Chih-Chang Chang，Chern-Lin Chen.Automatic phase-shift method for islanding detection of grid-connected photovoltaic inverters [J]. IEEE Trans on Energy Conversion，2003，18（1）：169-173.

[12]杨秋霞，赵清林，郭小强（Yang Qiuxia，Zhao Qinglin，Guo Xiaoqiang）.三相光伏并网逆变器电流扰动孤岛检测建模及分析（Modeling and analysis of current-disturbance based islanding detection for three-phase photovoltaic grid-connected inverters）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（4）：45-49.

[13]Jeong J B，Kim H J. Active anti-islanding method for PV system using reactive power control [J]. Electronics Letters，2006，42（17）：1004-1005.

[14]Chung S-K.Phase-locked loop for grid-connected threephase power conversion systems [J]. IEE Proceedings-Electric Power Applications，2000，147（3）：213-219.