基于VAR 模型的商业银行信用风险与经济周期关系的实证研究

张 琳

（青岛大学，山东 青岛 266071）

一、引言

信用风险（Credit Risk）是商业银行所面临的风险中最为重要的一类。近年来，伴随着我国经济的高速发展，银行业迅速扩张，信贷业务急剧膨胀，同时在全球一体化、金融管制放松和金融创新加快的背景之下，商业银行的信用风险管理面临着更加严峻的挑战。商业银行作为金融体系中的重要一环，其稳健性对整个金融体系至关重要。

商业银行的信用风险受到多种因素的影响。作为强周期性行业，商业银行受经济周期的影响较大，在经济扩张时期和经济萧条阶段，银行对未来经济走势预期的态度不同，而愿意承担的风险和信贷标准也不一，进而信贷规模的不同会是信用风险水平呈周期性波动。时滞效应可能会进一步增大信用风险管理的复杂性。因此加强信用风险水平与经济周期之间的关系研究，对于加强商业银行的风险调控、维持金融稳定进而促进国民经济健康高速发展具有重要的现实意义。

本文利用向量自回归模型(VAR)对我国商业银行与宏观经济变量进行动态分析，根据2004 年到2012 年的季度数据建立VAR模型，通过脉冲响应函数和方差分解技术分析主要宏观经济变量的冲击对我国商业银行信用风险水平影响的传递效应以及对信用风险水平的贡献程度。

二、理论分析

本文主要采用多维时间序列模型的最核心内容之一的向量自回归模型（Vector Autoregression，VAR）对我国商业银行信用风险水平与宏观经济变量的关系进行实证研究。

VAR 模型的实质是考查多个变量之间的动态互动关系。考虑一组变量y1t，y2t，…，ynt，那么实际上每个变量都是一个时间序列变量。这样我们可以将这些变量定义在一个n 维的向量Yt上，即定义一个n×1 的向量时间序列：

一个p 阶的VAR 模型，即VAR（p）,定义为：

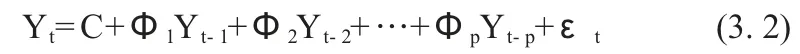
其中，C 表示n×1 维常数向量；Φi(i=1，2，…，p)表示n×n 维自回归系数矩阵；εt表示n×1 维的向量白噪音，满足：

其中Ω 表示n×n 的对称正定矩阵。

可以看出VAR 模型实际上刻画的是每个序列都对所有序列的滞后期，包括其自身的滞后期。本文即运用VAR 模型将商业银行信用风险指标序列对包括其本身和宏观经济变量的所有序列的滞后期进行回归，以研究信用风险与宏观经济的动态关系。

三、实证分析

（一）样本数据选取

本文选取不良贷款率作为衡量商业银行信用风险的指标，即：商业银行体系的不良贷款率越高，其信用风险水平就越高。不良贷款率的数据来源于中国银监会网站的统计数据，笔者选取了2004年一季度到2012 年二季度①的商业银行不良贷款率②p。根据《贷款质量评估指导原则》，中国的贷款按照五级分类法进行分类，不良贷款率=（次级+可疑+损失）/ 贷款总额。

宏观经济变量方面主要考虑三类指标。第一类，国民经济增长指标，以GDP 增长率为代表；第二类，通货膨胀指标，以CPI 为代表；第三类，金融市场指标，广义货币增长率M2 为代表。选取三个指标的2004 年至2012 年的季度数据，样本容量为34。从2004 年一季度到2012 年二季度，中国宏观经济走势基本经历了一个经济周期。2007 之前中国经济平稳高速增长，物价稳定，出现繁荣阶段；之后经历美国次贷危机引发的全球性的金融危机，货币当局采取积极的货币政策，松动银根，经济下行，2009 年基本见底；之后经济回暖到2011 年年底，基本达到危机前水平，但物价水平受危机中政策影响有走高势头。

（二）数据分析与处理

1.logit 模型转换。参照相关研究，笔者将不良贷款率p 通过logit 模型转换为中介指标y，转换公式为：

其中0＜p＜1，则有-∞＜y＜+∞。易知y 与p 负相关，即不良贷款率越高（信用风险越大）则y 值就越小。

2.单位根检验（ADF 检验）。利用VAR 模型进行回归分析，如果是分析不同变量之间可能存在的长期均衡关系，则可以直接选用非平稳序列；而如果分析的是短期互动关系，则应该选用平稳序列。本文分析商业银行与宏观经济变量的关系研究，用季度数据分析长期的均衡关系，可以直接选用非平稳序列。但使用非平稳序列进行回归会造成虚假回归，因此为了保证回归结果的无偏性、有效性和最佳性，我们利用扩展的迪克-福勒(ADF)检验方法来检验样本数据的时间序列特征检验结果如下表:

表1 单位根检验结果

ADF 检验结果显示，y、RGDP、CPI 和M2 原始数据在5%的显著性水平下都是非平稳序列，一阶差分数据在5%显著性水平下都是平稳序列，因此都是一阶单整序列即I(1)序列，可能存在协整关系。

3.协整检验。协整分析是基于非平稳序列之上的，对各序列的ADF 检验表明各变量都为I(1)序列，符合协整检验的条件。应用Johansen 检验方法对各个指标之间的协整关系进行检验，选择滞后阶数为4，得出两个模型的协整检验结果显示，在5%显著性水平下各模型都只有一个协整方程，模型各变量之间存在长期协整关系。

（三）实证分析

1.建立实证模型。在以上分析的基础之上，我们建立信用风险与宏观经济变量的无约束VAR 模型。

则p 阶的VAR 模型，即VAR（p）,为：

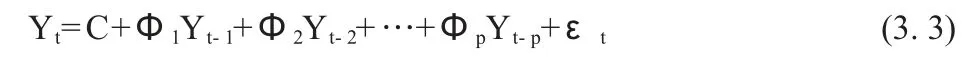
其中，C 表示4×1 维常数向量；Φi(i=1，2，…，p)表示4×4 维自回归系数矩阵；表示4×1 维的向量白噪音。

2.模型滞后期选择。理论上，我们希望选择的VAR 模型中的随机扰动项服从向量白噪音过程，选择合适的滞后期至关重要。运用Eviews6.0 对所建模型进行滞后期的判断，结果如下：

表3 滞后期数判断结果

通过结果可以判断，五个指标中有三个显示最优期数为3③，因此按“多数原则”应该选择VAR（3）进行后续分析。即p=3。

3.模型估计。对于已建立的VAR（3）模型运用最小二乘估计（OLS）④。根据估计结果的各个系数对应的t 统计量判断单个系数的显著性水平，剔除系数不显著的变量，得估计模型如下（中括号中为t 统计量）：

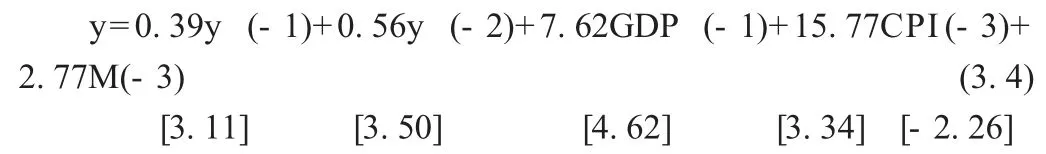
4.平稳性检验。VAR 模型的平稳性主要是指弱平稳性。如果以下条件满足，则对应的VAR 模型是平稳的，即：

其中，Γj定义的是Yt在第j 期的自协方差矩阵。

式(3.5）给出的是笼统的平稳VAR 模型的定义。对于具体的VAR（p）模型，其平稳性条件是逆特征方程：

它的根全部落在单位圆外，或者特征方程：

它的根全部落在单位圆内。

Eviews 检验单位根分布图如下：

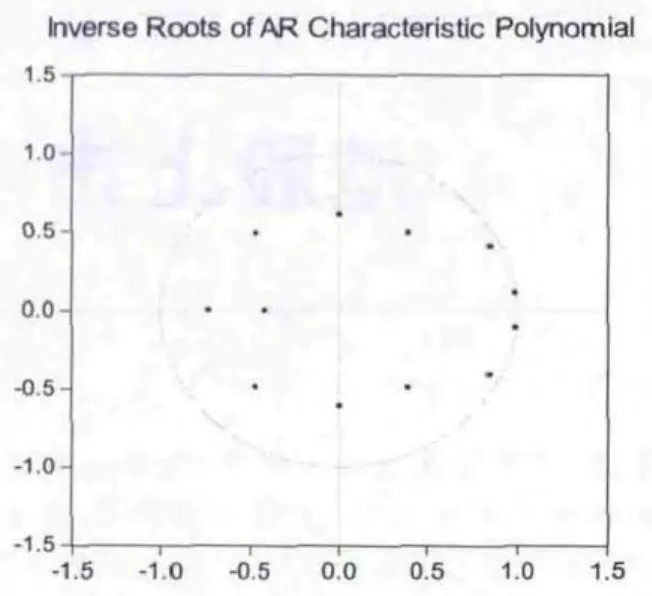
图1 单位根分布图

可见VAR(4)模型的单位根全部落在单位圆内，模型是平稳的，可以进行脉冲响应和方差分解分析。

5.脉冲响应函数。VAR 模型是一个复杂的模型系统，我们考虑的是整个系统中的互动关系，单个系数只是反映了一个局部的动态关系，而并不能捕捉全面复杂的互动过程。因此，VAR 模型中系数作用就不是很大，而与VAR 模型相关的脉冲响应函数（Impulse Response Function，IRF）却能够比较全面地反映各个变量之间的动态关系。

图2 VAR(4)模型脉冲响函数

本文运用 Eviews6.0 选择乔莱斯基分解（Cholesky Decomposition）的方法来求脉冲响应函数，图形如下。说明，GDP 增长率、CPI、M2 增长率的波动都对不良贷款率的中间变量y 有长期的动态影响，影响呈现周期性。

6.方差分解。脉冲响应函数能够反映出一个变量的冲击对另一个变量影响的动态路径，而方差分解（Variance Decomposition）可以将VAR 系统内一个变量的方差分解到各个扰动项上。因此，方差分解提供了每个扰动因素影响VAR 模型内各个变量的相对程度。

表4 方差分解结果

四、结论

本文采用我国2004 年1 季度到2012 年2 季度的宏观经济数据和商业银行的不良贷款率数据，通过建立模型并进行分析，得出GDP 增长率、通货膨胀率、广义货币增长率对我国商业银行的信用风险影响显著。

从时间关系上看，主要宏观经济变量与不良贷款率之间具有相对稳定的滞后期，约为1 至3 期，即在经济进入下行期时，上行期积聚的信用风险会在GDP 增速放缓的过程中逐步暴露。从相关关系上看，GDP 和CPI 的滞后变量与中介变量y 成正相关关系，进而与不良贷款率p 成负相关关系；M2 的3 期滞后变量与p 成负相关关系。从数量关系上看，GDP 增速每变化一个百分点，不良贷款率反向变化约1.7 个百分点。

鉴于本文的研究结论，可以看出宏观经济变量和商业银行信用风险之间有着密切的联系，在几年来的次贷危机和欧债危机中我国的商业银行虽没有受到大的冲击，但应该吸取欧美大银行在这次危机中的教训，防患于未然，提高自身的风险意识，继续降低银行的不良贷款率。另外，政府在遇到宏观经济问题时，货币政策起着至关重要的作用。一国货币当局在面对危机时，应该审时度势，制定正确的货币政策，确保经济的快速增长。

注释

①中国银行业监督管理委员会成立于2003年4月，自此开始公布银行相关数据，笔者选取此后的数据认为比较可靠。

②商业银行包括大型商业银行、股份制商业银行、城市商业银行、农村商业银行和外资银行。

③“*”表示该指标显示为最优滞后期数。

④估计结果见附表1。