静力学受力分析教学方法研究——基于“自由度”理论

何 洋，修树东，姚文斌

（浙江农林大学暨阳学院，浙江绍兴 311800）

理论力学是工科专业的一门技术基础课，在工科专业中有举足轻重的作用［1］，包含静力学、运动学和动力学3个部分。其中，静力学主要研究物体在外力作用下的平衡规律。在静力学中，受力分析又是最基本、最重要的内容之一，能否对受力物体进行正确的受力分析并画出受力图是学习静力学的关键［2］。

笔者在教学过程中发现传统的受力分析方法学生掌握起来比较困难，要同时记住约束的类型和约束力的形式和方向。本文提出一种基于自由度理论的分析方法，以便降低学生学习的难度。

一、传统受力分析方法

对于受力分析，现有理论力学教材普遍采用的方法是:先定义约束，然后根据约束确定约束力的个数及约束力的方向，最终画出受力图，从而确定物体的受力状态，为后续力系的分析过程打下基础。

约束就是对非自由体的运动施加的限制其运动的条件。自由体在空间是不受约束的，因此可以移动到空间任一点，在这一点上又有很多种姿态。

根据物体受力的状态和受力分析的基本要求，将约束分为如下几种类型:

1.柔绳约束。柔绳约束只能约束一个方向的自由度，并且只能受拉，所以它们的约束力是作用在接触点，方向沿绳索背离物体。这类约束包括绳索、带传动、链传动等。

2.光滑接触面约束。光滑接触面约束提供的约束力为支持力，约束力作用在接触点处，方向沿公法线，指向受力物体。这类约束主要指无摩擦滑块的约束。

3.辊轴约束。辊轴约束与光滑接触面约束类似，约束力作用在接触点处，方向沿辊轴下表面的平面的公法线。这类约束跟光滑表面约束类似，都是垂直于表面的公法线，但辊轴约束可以背离受力物体。

4.铰链约束。铰链约束分为固定铰链约束和中间铰链约束两种类型。固定铰链约束是由销轴约束销孔，为一个约束力，但方向很难确定。为便于确定孔销传力的方向，一般采用两对正交的力来代替，常用一个水平力Fx和一个垂直力Fy来代替。中间铰链约束与固定铰链约束类似，也是用一对正交的力Fx和Fy来表示，主要区别是固定铰链约束是由支座提供的约束，而中间铰链约束是由连接的另外一个构件提供的约束。将铰链约束推广到空间力系，为球铰链约束，其约束力为互相正交的3 个力 Fx、Fy和 Fz。

5.固定端约束。固定端约束分为平面固定端约束和空间固定端约束。平面固定端约束的约束力同样为一对正交的力Fx和Fy，除此之外，还有一个力偶矩MO。空间固定端约束是对平面固定端约束的推广，约束力为3个力Fx、Fy和Fz和3个力偶Mx、My和Mz3个力矩。

二、传统方法存在的问题

除上述5种约束之外，还有一些变通的约束。学生要想掌握、运用这些约束和约束力进行受力分析并不容易。学生首先要能够在老师的介绍下记住这些约束，并且要搞清楚这些约束之间有何区别和联系，否则很容易弄错。因此，学生在学到这部分的时候普遍感到困难，作业错误率也较高，严重影响受力分析的正确性，进而影响到力系的相关计算。

这些问题说明，原有教学方法虽然能够让学生学会约束和约束力，并进行受力分析，但学生接受时间长。说明这种方法已经不能适应当前教学的需求，特别是导致学生学习基础薄弱和学习态度不积极情况的发生。为此，笔者提出一种基于“自由度”理论的受力分析方法，将所有约束合为一体，直接根据物体的实际状态来分析，掌握一种即能举一反三，全面掌握受力分析。

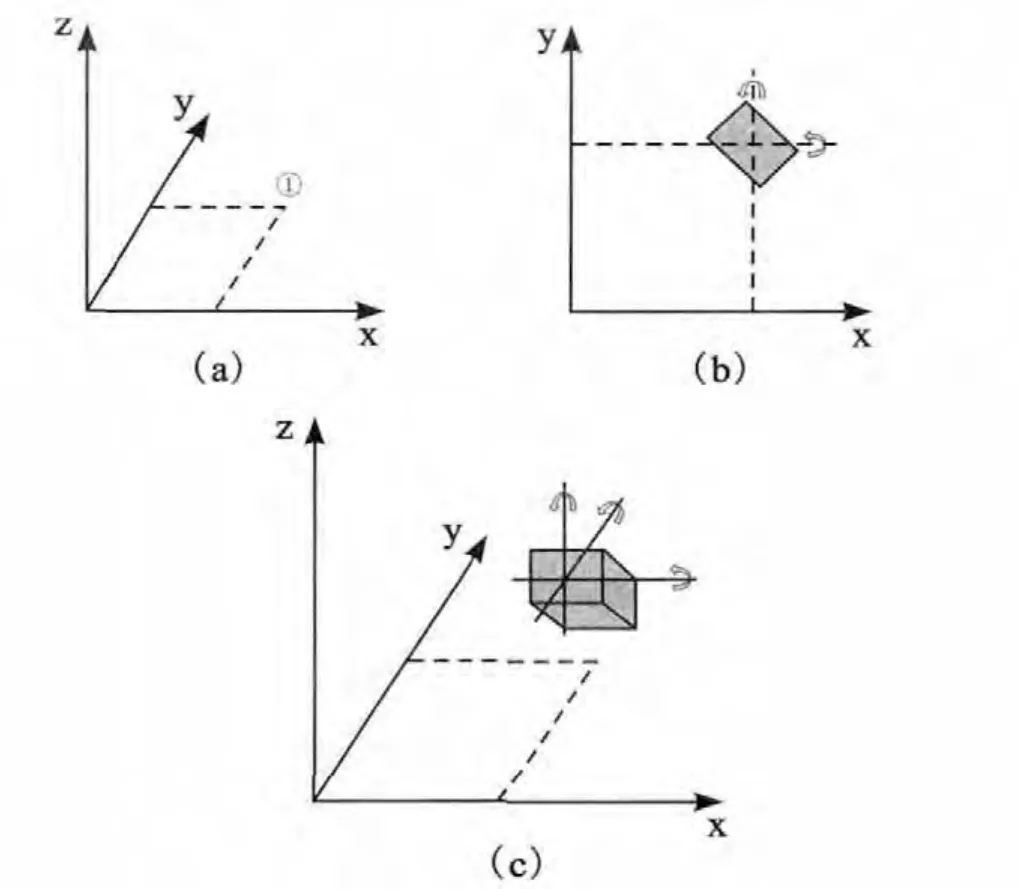
图1 自由度分析图

三、基于“自由度”理论的受力分析方法

“自由度”在各行业均有定义，机械科学里讲的“自由度”是这样定义的:唯一确定质点系空间位置的独立参变量个数，力学中完全决定力学体系在空间的位置所需的独立坐标的数，叫做力系的“自由度”［3］。这里的“完全”是指组成体系的所有各个质点的位置。具体分析如下:

1.自由质点的自由度。自由质点为一个没有大小的点，只有位置，没有姿态，因此自由度为3。如图1（a）所示。

2.平面上自由刚体的自由度。平面内自由刚体的位置由x、y两个坐标来表示，除位置外，还有刚体在这个位置上的姿态，姿态可以用绕坐标原点O的旋转角来表示，因此有3个自由度，如图1（b）所示。

3.空间自由刚体的自由度。空间自由刚体有6个自由度:3个平移自由度和3个转动自由度。如图1（c）所示。

利用“自由度”理论来分析约束力的方法为:根据物体或物体系中刚体的之间或者刚体和基座之间的连接状态来分析物体自由度的减少，哪一个平移自由度被限制了，相应这一个方向就有力存在，并且跟被限制运动的方向相反;哪一个方向的转动自由度被限制了，相应的这一方向就有力偶存在。判断起来既直观又方便，完全不用记忆原来的各种约束。下面通过一个案例进行分析。

四、案例分析

在图2所示的平面系统中，AF为绳索，B为固定铰链，C为质量块，质量块与杆件之间的摩擦力忽略不计，D为辊轴，E为固定端，利用传统方法和基于自由度理论的受力分析过程如图2。

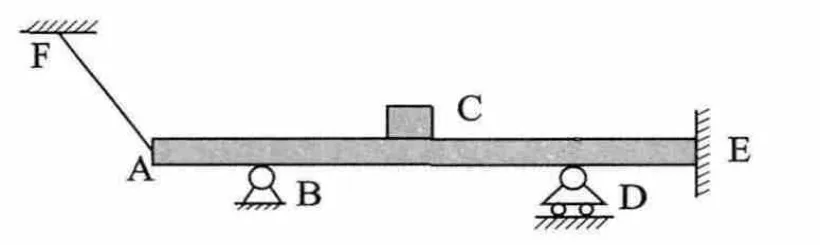
图2 平面力系

1.传统方法分析过程。以杆AE为研究对象进行受力分析，该杆件分别在A、B、C、D、E 5个地方存在着约束力，首先要搞清楚这几个点处的约束类型:A点为柔绳约束，受力沿着绳子方向，背离物体;B点为固定铰链约束，用一对正交的力FBX和FBY来表示;C点为光滑表面约束，受力方向沿着公法线方向，指向杆件，用FC来表示;D点为辊轴约束，受力方法沿着公法线方向;E点为固定端约束，用一对正交的力FEX和FEY和绕E点的力矩ME来表示。因此受力图如图3所示:

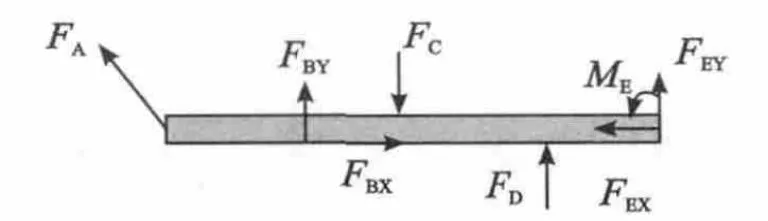
图3 杆AE的受力分析

2.基于自由度理论的分析方法。以杆AE为研究对象进行受力分析，分别分析这5个点处的自由度被限制的情况:A点的绳子只限制了杆件背离F点的运动，并且是单向的，故力沿着AF方向;B点限制了杆件水平方向和竖直方向的平移，但还可以绕B点旋转，故受的力为FBX和FBY;C点只限制竖直向上的运动，故受力为竖直向下，用FC来表示;D点很明显限制了竖直方向的运动，跟FC类似;E点杆件被固定在基座上，不仅不能沿着X和Y方向平移，也不能绕E点转动，因此，用FEX和FEY和ME来表示，分析结果如图3所示。

比较两种方法可以看出，得出的受力分析结果完全一致，但用第二种方法仅仅根据对实际现象的理解，通过自由度被限制的数量和形式，来确定力和种类和方向，方便使用，并且对各种约束都适用。

笔者将这种方法应用于2013年《理论力学》的教学实践过程中，学生在受力分析和力系的求解计算过程中应用了该方法，跟2012年传统方法相比，学习效果有明显提升。传统方法和现有方法教学效果如表1所示。从表中可见，期末考试得分率有明显提升。

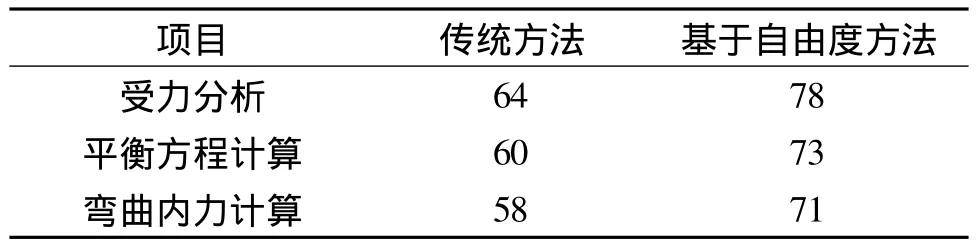
表1 传统方法和现有方法考试得分率比较 %

五、结语

在静力学受力分析部分的教学过程中，通过对约束力的分析的教学过程进行分析，发现使用传统教学方法学生学习起来比较困难，学习效果比较差，而基于“自由度”理论的受力分析方法简单可靠，在教学实践中效果良好，学生普遍对于受力分析掌握比较好，为后面的力系分析打下了坚实的基础。

［1］刘燕，李红梅，张华，等.浅谈静力学教学中的几点体会［J］.科技信息.2011（25）:617 －618.

［2］杨永明.力学课程教学改革探索［J］.河北农业大学（农林教育版），2012（4）:87 －89.

［3］靳毅，康艳霞.力学体系的自由度［J］.开封教育学院学报.1996（1）:44－48.

（编辑:王雅娇）