一种基于二次变异策略的改进型遗传算法

马福祥，马秀娟

青海师范大学计算机学院，西宁810008

1 引言

遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法。它最早由美国密西根大学的Holland教授提出[1]，起源于20世纪60年代对自然和人工自适应系统的研究。

目前，研究人员从染色体的编码方式[2-4]、遗传算子的选择[5-9]、遗传算法中相关参数的设定[10-11]，以及算法的收敛性[12-13]等方面对遗传算法进行了相关的研究，并得到了一些重要的结论。随着应用领域的不断扩大和实际工程问题的复杂化，遗传算法逐渐显现出一些不足和缺点，针对这些问题，一些改进的算法相继被提出[14-17]。改进的算法主要从物种多样性、个体适应度评价函数和遗传算子参数确定等方面进行了研究。研究结果表明，改进后的算法在个体多样性的保持，算法搜索能力的提高，全局收敛性的改善等方面取得了较好的效果。

以往的研究表明，为了保证遗传算法的全局收敛性，就要保持种群的多样性，避免有效基因的丢失。另一方面，为了加快算法的收敛速度，就要使群体较快地向最优状态转移，这又会减少群体的多样性，容易陷入局部最优点。本文在基本遗传算法的基础上，采用了单点位变异和倒置变异两次变异操作。通过仿真实验把改进后的算法应用到TSP问题的求解中，实验结果表明，二次变异策略能较好地保证群体的多样性，同时算法也能较快收敛到最优状态，算法的搜索能力得到了提高，搜索到了更优的适应度值。另外，相同条件下当增大种群规模时，二次变异后的算法得到的解比基本遗传算法更优。

2 TSP问题描述及改进遗传算法

2.1 TSP问题描述

旅行商问题（TSP）是一个具有广泛应用价值和重要理论意义的典型组合优化问题。可以简单描述为：给定n个相互联系的城市，有一个旅行商从某一个城市出发，访问各城市一次且仅一次再回到原出发城市，要求找出一条最短的巡回路径。

该问题的数学描述为：设集合C={c1，c2，…，cn}是n个城市的集合，其中每对城市之间的距离d(ci，cj)∈R+，求一条经过C中每个城市一次且仅一次的路线(cπ1，cπ2，…，cπn)，使得下列目标函数最小：

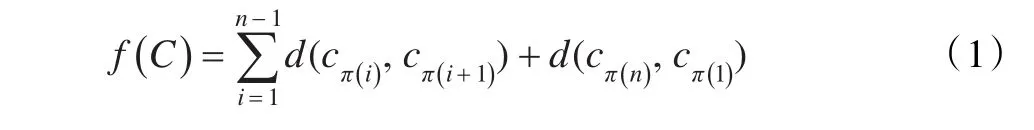
2.2 改进遗传算法及其解决TSP问题的基本思想及操作步骤

本文通过改进基本遗传算法中的变异策略，增加了变异次数，采用了单点位变异和倒置变异两种变异策略来提高算法效率，使得算法在解决TSP问题时搜索到的解比传统的一次变异更优。

改进后的算法解决TSP问题的基本思想为：在随机生成的M个城市的N条巡回路径中（N个种群）进行全局搜索，搜索时采用交叉和变异策略。在应用变异策略是，将传统的单次变异策略改进为二次变异，即在单次变异策略的基础上对得到的种群进行二次变异，再对得到的新种群通过个体适应度函数计算比较每个新种群的个体适应度值，最终得到TSP问题的近似最优解。

根据改进后的遗传算法得到了该算法解决TSP问题的操作步骤，具体如下所述：

（1）随机生成M个城市的N条路径构成的初始种群p(N)，并进入循环；

（2）对初始种群中p(N)中的个体进行两两交叉操作，形成新的种群个体；

（3）对交叉操作后形成的新个体计算其适应度值，并与交叉前的旧个体进行比较，保留适应度值较优的个体；

（4）对交叉操作结束后种群中的每个个体进行第一次变异，得到新的种群个体；

（5）对变异后的个体计算适应度并与第（3）步得到的结果进行比较，选出局部最优的种群个体；

（6）对第一次变异后得到的种群中的每个个体进行二次变异，得到新的种群个体；

（7）对倒置变异后的种群个体计算适应度值，并与第（6）步中得到的个体适应度值进行比较，得到局部最优值；

（8）记录上一代的最优值，并进入下一代循环执行第2到第7步；

（9）迭代次数超过最大迭代数，循环终止，输出全局最优值。

3 改进遗传算法的仿真实现及数据分析

3.1 改进遗传算法的仿真实现

通过用M atlab编写仿真实验程序对上述算法进行了仿真实验，实验结果表明：改进后的遗传算法在解决TSP问题时能更有效地保持个体的多样性，并有效提高算法的局部搜索能力，得到了比单次变异更优的解。

遗传算法中种群个体的编码方式、交叉和变异策略的设计对最终的结果有直接的影响。本文的仿真实验在种群个体的编码方式上采取了常用的“路径编码串”的编码方式，即直接采用城市在路径中的位置进行表示，这种编码方式能更简单直观地表示种群个体和路径之间的关系。根据TSP问题是求解经过每个城市一次且仅一次的最短闭合路径的特点，本文使用了启发式交叉策略。即随机选择两条路径串，并随机确定两个串的交叉区域段，交换删除两个串中在交叉区域出现的城市，然后将剩下的城市与交叉区域中的城市组成一个新串。变异操作是算法产生新个体的辅助方法，决定了遗传算法的局部搜索能力，保持了种群的多样性。本文为了提高遗传算法中种群的多样性，提高算法的搜索能力找到更优的解，在算法的变异策略上采用了二次变异策略，即采用单点位变异和倒置变异两种变异策略。单点位变异是指随机选择一个串，确定两个交叉变异点，交换两点上的城市编号得到新的路径串；倒置变异是指随机确定路径中的倒置变异区域，然后将该区域中的城市编号进行倒置得到新的路径串。通过仿真实验，可以得到如图1所示的最短路径。

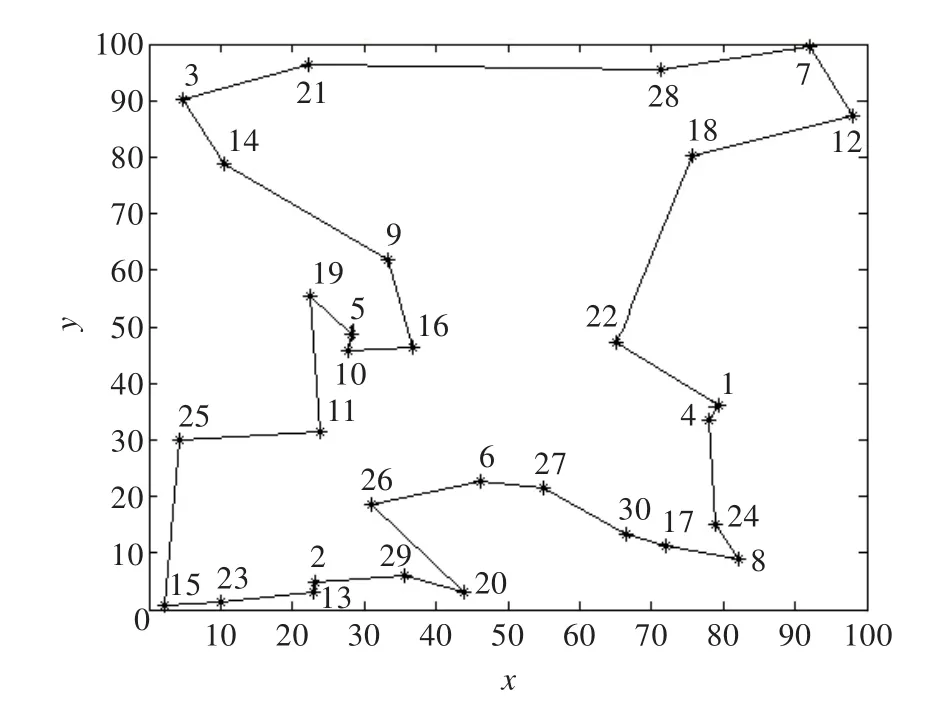
图1 30个城市的最短路径

3.2 改进遗传算法的仿真实验数据分析

为验证本文提出的改进遗传算法的有效性，设计仿真实验程序进行了验证。实验中的适应度函数如上述TSP问题描述中的公式（1）所示，相关参数的设置及取值由表1给出。

表1 改进遗传算法仿真实验各参数及取值表

为了保证实验的有效性，本文给出了30次实验的结果。图2给出了相同的种群规模和迭代次数下，二次变异的改进遗传算法与非二次变异的基本遗传算法的实验结果。

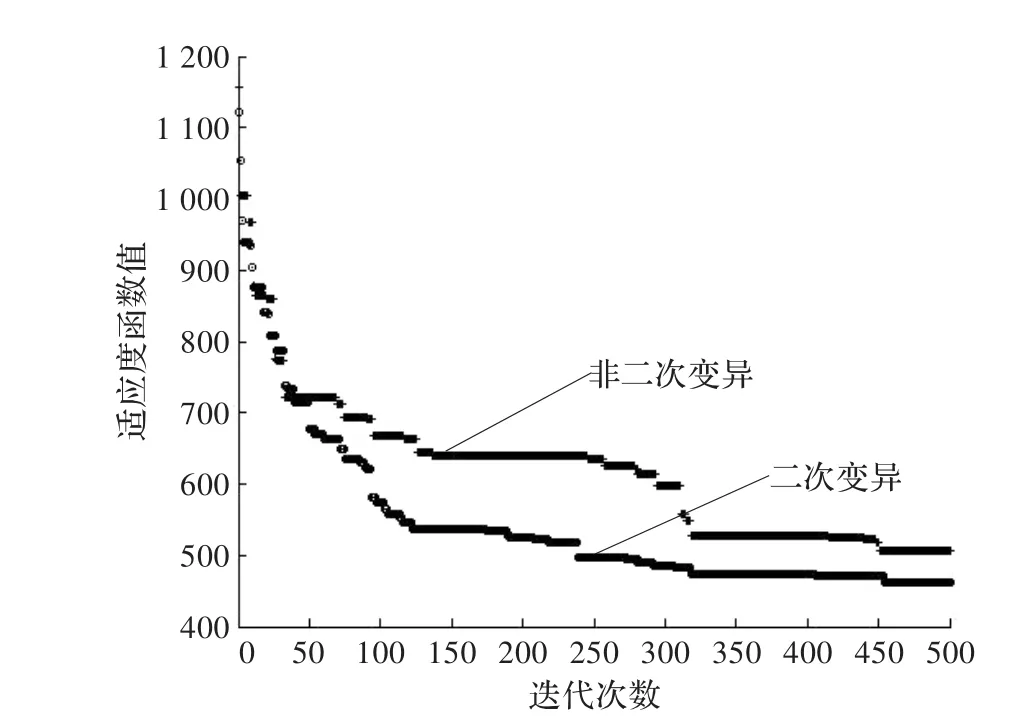
图2 二次变异与非二次变异适应度值曲线图

从图2中的曲线可以看出二次变异策略的改进算法能得到的适应度值更优。表2给出了适应度值在两种算法下，30次实验结果的最大值、最小值以及平均值。表2的结果表明，二次变异的改进算法找到的适应度值总是比非二次变异的基本遗传算法更优。

表2 两种算法下的适应度值比较

另外，在二次变异的改进遗传算法中，只要增大种群规模，改进的遗传算法比基本遗传算法能找到更优的适应度值。图3给出了种群规模对二次变异算法的适应度值的影响；表3给出了不同种群规模下改进算法的适应度值。

图3 相同迭代次数下种群规模对改进算法适应度值的影响

表3 不同种群规模下改进算法的适应度值

图3中的数据表明，二次变异的改进遗传算法对种群规模有很强的敏感性，当增大种群规模时，算法能找到更优的适应度值。表3中的数据表明，虽然基本遗传算法也对种群规模有一定的敏感性，但相同条件下二次变异的改进算法对种群规模的敏感性更强。仿真实验比较了30次实验找到的所有适应度值，并给出了不同种群规模下适应度的最小值、最大值和平均值。通过比较，进一步验证了在遗传算法中采用二次变异的策略有利于提高算法的搜索能力。

4 结语

通过在基本遗传算法中增加二次变异策略来改进算法，仿真结果表明，二次变异的改进遗传算法找的适应度值比基本遗传算法更优；另外，二次变异的改进算法对种群规模有更好的敏感性。改进后的算法更好地保持了种群的多样性，在提高算法的搜索能力上也有更好的效果。本文算法除了应用在TSP问题中外，还可以应用到复杂网络求解最短路径和平均路径长度等问题中，有一定的可扩展性。

[1]Holland J H.Adaptation in natural and artificial systems：an introductory analysis with applications to biology，control，and artificial intelligence[M].2nd ed.Cambridge：M IT Press，1992.

[2]Yang Xiaohua，Yang Zhifeng，Yin Xinan，et al.Chaos graycoded genetic algorithm and its application for pollution source identifications in convection-diffusion equation[J].Communications in Nonlinear Science and Numerical Simulation，2008，13（8）：1676-1688.

[3]梁旭，王佳，黄明.解决大规模生产调度问题的一种新编码方法[J].计算机集成制造系统，2008，14（10）：1974-1982.

[4]He Yaohua，Hui Chiwai.A binary coding genetic algorithm for multi-purpose process scheduling：a case study[J].Chemical Engineering Science，2010，65（16）：4816-4828.

[5]Tang Kezong，Sun Tingkai，Yang Jingyu.An improved genetic algorithm based on a novel selection strategy for nonlinear programming problems[J].Computers and Chemical Engineering，2011，35（4）：615-621．

[6]Boris P L，Jessica S C.A determ inistic annular crossover genetic algorithm optimisation for the unit commitment problem[J].Expert System s with Applications，2011，38（6）：6523-6529．

[7]Wang Lei，Tang Dunbing.An improved adaptive genetic algorithm based on hormone modulation mechanism for Job-Shop scheduling problem[J].Expert Systems with Applications，2011，38（6）：7243-7250．

[8]巩敦卫，郝国生，严玉若.交互式遗传算法基于用户认知不确定性的定向变异[J].控制与决策，2010，25（1）：74-78．

[9]Murat A，Novruz A.Development a new mutation operator to solve the traveling salesman problem by aid of genetic algorithm s[J].Expert Systems with Applications，2011，38（3）：1313-1320.

[10]闫利军，李宗斌，杨晓春.基于混合优化算法的遗传算法参数设定研究[J].系统工程与电子技术，2007，29（10）：1753-1756.

[11]李慧贤，庞辽军，蔡皖东.基于信息熵对遗传算法中杂交概率的研究[J].系统工程与电子技术，2009，31（7）：1743-1745.

[12]喻寿益，邝溯琼.保留精英遗传算法收敛性和收敛速度的鞅方法分析[J].控制理论与应用，2010，27（7）：843-848.

[13]马永杰，马义德，蒋兆远，等.一种快速遗传算法及其收敛性[J].系统工程与电子技术，2009，31（3）：714-718.

[14]孟伟，韩学东，洪炳镕.蜜蜂进化型遗传算法[J].电子学报，2006，34（7）：1294-1300.

[15]鲁宇明，黎明，李凌.一种具有演化规则的元胞遗传算法[J].电子学报，2010，38（7）：1603-1607.

[16]Zhang Jinhua，Zhuang Jian，Du Haifeng，et al.Self-organizing genetic algorithm based tuning of PID controllers[J].Information Sciences，2009，179（7）：1007-1018.

[17]Li Fachao，Xu Lida，Jin Chenxia，et al.Intelligent Bionic Genetic A lgorithm（IB-GA）and its convergence[J].Expert Systems with Applications，2011，38（7）：8804-8811.