堆场取箱作业中倒箱问题的启发式算法研究

范 磊，梁承姬

(1.上海海事大学 物流工程学院，上海 201306；2.上海海事大学 物流研究中心，上海 201306)

0 引 言

近些年集装箱运输快速发展，与此同时，由于土地的局限性、码头规划的滞后性等原因，码头堆场正承受越来越重的负荷。因此，为了利用了更多的堆场空间，码头堆场的堆垛层越来越高，采用混堆模式的码头个数也随着增多，这些改变必然的导致倒箱量的增多。倒箱量和倒箱率无疑都是衡量码头操作效率的重要指标，而在如今这个港口之间竞争如此激烈的大环境中，高效的运作效率无疑是港口增强竞争力的关键因素。倒箱操作，发生在船舶上的装船、卸船及在岸边出口箱装船、前后方堆场集装箱提箱、箱区整理及堆存过程中，几乎是一个不可避免的环节。要彻底解决倒箱问题非常困难，因为它与装船计划、堆存计划、提箱计划都息息相关。

由于倒箱耗费巨大的时间成本和装卸成本，于是学者们对于倒箱问题的研究也不断增多与深入。K.H.Kim[1]在1997年提出倒箱量估计方法，研究了码头进口箱区堆存高度与倒箱量之间的关系，并针对不同进口箱到达模式，建立了最小化期望倒箱量为目标的数学模型，利用拉格朗日松弛和次梯度优化方法求解出相应的最佳堆存高度；在集装箱码头的出口堆场中，通常重箱先于轻箱装船，基于这一假设，K.H.Kim，等[2]在2000年以最小化装船时的倒箱量为目标，利用动态规划和决策树方法研究了进口集装箱堆放位置的确定问题；K.H.Kim，等[3]在2006年利用分支定界和启发式方法研究了提箱过程中翻倒集装箱落箱位置的确定问题；张维英，等[4]建立了龙门式起重机小车取箱作业优化模型,以龙门式起重机取箱作业时倒箱数量最少为目标, 以各个取箱阶段为节点、以取箱代价为边的权数, 应用最小生成树和启发式算法对优化模型进行求解；白志江，等[5]提出堆场翻箱问题的整数规划模型，对已知的初始堆码状态, 在同一个贝位内倒箱, 使其最终堆码状态满足积载计划规定的装船次序, 目标是使倒箱次数最少，并提出了以网络流模型为基础的倒箱数学模型, 节点和有向弧对应于贝位的时空结构, 箱子在时空中的移动用流来表示, 约束指定了所要遵循的物理规律；李斌[6]利用动态规划方法对倒箱问题进行阶段性研究。

随着集装箱堆场倒箱问题的不断凸显，对于解决倒箱问题的算法的时效性、准确性也提出了更高的要求。因此，笔者研究了贝位内取箱作业问题，结合集装箱的目的港和重量两个属性[7-8]，每一个箱子被赋予一个优先级别，然后按照优先级别进行取箱作业，以倒箱量最少为目标，建立龙门吊起重机取箱作业(图1)的数学模型，再应用基于6条倒箱落位原则的启发式算法对数学模型进行求解；经验证，启发式算法可获得较优的可行解，稳定性强，提高了取箱作业的效率。

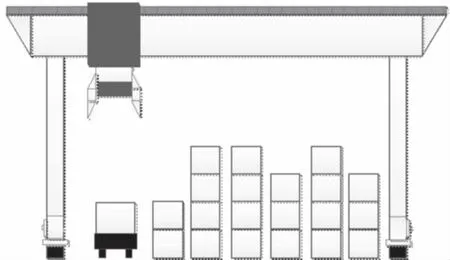
图1 龙门吊起重机配合集卡取箱作业示意Fig.1 Schematic diagram of retrieving operation via the cooperation of gantry crane and container trucks

1 问题描述

在集装箱堆场中，垂直堆放的一列集装箱成为一个栈，并排堆放的若干个栈组成一个贝(图2)。所谓的倒箱，如果要提取的集装箱不处于所在栈的最高层，就必须首先将堆放在其上的所有集装箱倒到其它栈，这个过程就称为倒箱。

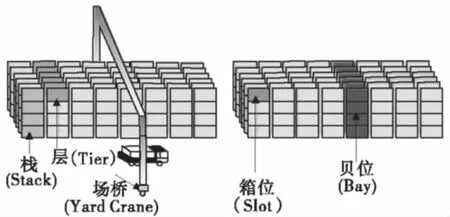
图2 集装箱箱区示意Fig.2 Schematic diagram of container blocks

贝位的初始状态及各集装箱的发箱顺序已知，针对不同的集装箱类型，发箱顺序的确定需要考虑不同的因素。如果是出口箱，目的港和重量是主要考量的因素；如果是进口箱，那么预定的取箱时间是主要考量的因素。假设贝位初始状态如图3，顺序越小，发箱的优先级别越高，即顺序为1的集装箱是最先发箱的，0表示空箱位。那么问题就变得异常清晰，即按照各箱子发箱的优先级别依次取箱。确定发箱顺序的目的是使得整个取箱过程中倒箱量最少。

图3 贝位初始状态示意Fig.3 Schematic diagram of initial state of a bay

2 取箱作业数学模型

2.1 模型基本假设

1)贝位内的集装箱具有相同的尺寸；

2)在堆存初始状态已知的情况下，各箱的取箱顺序已知；

3)仅对待提箱上方的集装箱进行倒箱操作；

4)堆存为N层，则贝位内至少有(N-1)个空箱位被留作倒箱使用，倒箱操作只发生在贝位内，不同的贝位取箱作业模型一致；

5)提箱过程中，不允许新到集装箱在相应场区进行堆放。

2.2 模 型

2.2.1 参数设置

A[m,n]表示m层n栈，用矩阵的形式来表示一个单独贝位的堆垛情况，矩阵中的各元素代表该位置上箱子的取箱优先级别，以图3来说明，则是一个6层5栈的贝位;

A(t,i,j)=C表示在t阶段A(i,j)箱位上箱子的优先级别，其中C表示从0开始的某一整数；

slot_priority={0,1,2,3,…,C}为由箱子取箱优先级别组成的集合；

stack(s)={1,2,…,s}为贝位所有堆垛列组成的集合；

tier(h)={1,2,…,h}为贝位所有堆垛层组成的集合；

stage(t)={1,2,…,t}表示由不同的装载阶段组成的集合，每搬移一次箱子为一个stage；

High_of_stack(s)=h表示s栈的最高堆垛层为h，其中h表示从0开始的某一整数；

Shelve(s)=h表示s栈中优先级别最大的箱子上面箱子的数量，称为压箱量，其中h表示从0开始的某一整数；

Cost_of_Catch(C)表示取优先级别为C的箱子的取箱代价，即待取箱上面有的需要倒箱的集装箱数，其中C是属于slot_priority的某一整数；

2.2.2 变量设计

2.2.3 压箱量的计算

在某一个阶段，贝位中集装箱的堆垛状态已知，每一栈中提箱优先级别最大的(即数值最小)的箱子所在的层数是确定的，这里的层数是从上至下增加的，即栈最上面的是第1层，原因是为了和MATLAB语言中读取这样一个代表贝位状态的矩阵的顺序一致；而每一个堆垛栈(stack)的最高堆垛层High_of_stack(s)也是确定的，但是最高堆垛层High_of_stack(s)是从下至上增加的，即栈最下面的为第1层。所以计算压箱量shelve(s)时先要进行转换。

假设研究的贝位是m层的，而第s栈中最大优先级别的箱在d层，那么转换的式子是e=m+1-d;而压箱数shelve(s)=High_of_stack(s)-e;如图3所示贝位层数m=6;其中第1栈中，High_of_stack(1)=3，最大优先级别的箱子是3，在第5层(d=5)，经公式e=m+1-d转换后得e=2;再经压箱数计算公式shelve(1)=High_of_stack(1)-e得shelve(1)=3-2=1。更新一个阶段后，shelve(s)需要重新更新。

2.2.4 目标函数

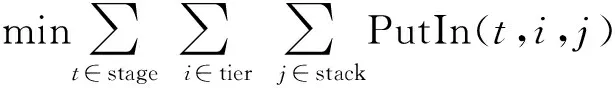
(1)

式(1)为目标函数，表示倒箱数量最少，因为产生倒箱时才产生PutIn。

2.2.5 约束条件

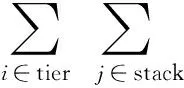
(2)

式(2)表示每一个stage(t),有且仅有一个移动，要么一个箱子被提出，要么一个箱子被放入。

A(t,i-1,j)=0 & A(t,i,j)≠0:PutIn(t+1,i-1,j)=1；∀t∈stage,∀i∈tier,∀j∈stack

(3)

式(3)表示在t这个阶段A(i,j)上有箱子并且A(i-1，j)上没箱子的条件，PutIn(t+1,i-1,j)这个移动才会被执行。

A(t,i-1,j)=0 & A(t,i,j)≠0:TakeOut(t+1,i,j)=1；∀t∈stage,∀i∈tier,∀j∈stack

(4)

式(4)表示在t这个阶段A(i，j)上有箱子并且A(i-1，j)上面没箱子的条件，TakeOut(t+1,i,j)这个移动才会被执行。

(5)

式(5)表示提箱次数和取箱次数的总和组成所有的作业阶段，总和为T。

其中，层tier是从上到下(1,2,…)数值增大排列的，栈stack是从左到右(1,2,…)数值增大排列的。

3 贝位内取箱作业启发式算法

当贝位内集装箱被赋予不重复的优先级别之后，取箱操作(流程如图4)就转化成一个动态规划问题，一个多阶段决策过程的最优化问题。取一个优先级别的箱子可视为一个阶段，而倒箱操作势必影响前后阶段的决策。

动态规划问题求解最优解时，要考虑所有可能的链结构，复杂度是随着问题规模的增长成指数增长的。集装箱码头对算法的时效性要求非常高，所以需要用启发式来求解。

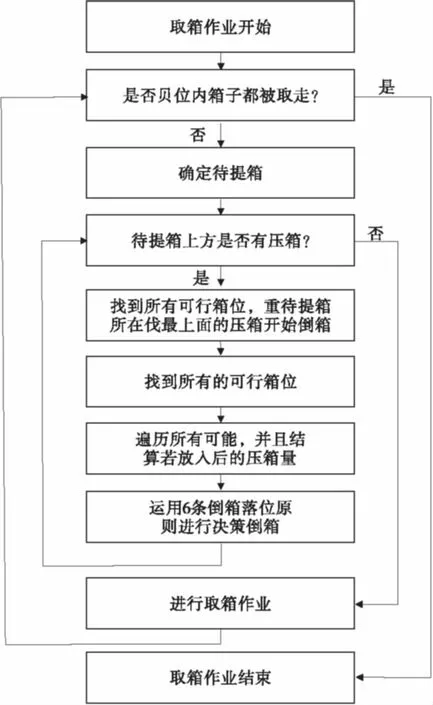
图4 取箱作业流程Fig.4 Diagram of retrieving operation process

倒箱问题中，倒箱落位是关键。因为倒箱落位的选择决定了2次倒箱甚至多次倒箱的数量。所谓2次倒箱即堆场机械由于各种作业的需要，为取堆存在下面的集装箱而把上面的箱子移开(此时产生第1次倒箱)，但上方的集装箱移开后放置的位置可能将导致另一次倒箱[9]。倒箱落位决策中，以最小化总倒箱量为目标，同时以尽量避免单次取箱时倒箱操作过多[10]；而文中的启发式算法是基于3.1节的6条倒箱落位原则的。

当取箱作业开始后，找到所有可行箱位，遍历一遍所有可能，把必倒箱放入所有的可行箱位，并且计算假如必倒箱放入后的该可行箱位所在的栈的压箱量，然后出现以下6种情形：

1)必倒箱放入可行箱位后，出现栈的压箱量为0，而该栈不是空栈，并且这样的可行箱位不唯一；

2)与情形1情况类似，但这样的可行箱位唯一；

3)必倒箱放入可行箱位后，出现栈的压箱量为0，而这样的可行箱位所在的栈为空栈，并且这样的栈不唯一；

4)与情形3情况类似，但这样的可行箱位唯一；

5)必到箱放入所有可行箱位后，前4种可能均不存在，比较下得出的各栈的压箱量，最小压箱量所在的栈不唯一；

6)与情形5情况类似，但这样的可行箱位唯一。

3.1 倒箱落位原则

原则1：若情形1存在，找到出现情形1情况的各可行栈中的最大优先级别(数值最小)，组成一个集合，然后选择这个集合中优先级别最低(数值最大)的箱子所在的栈，放入必倒箱。

原则2：若情形1不存在，情形2存在，直接将必倒箱放入该可行箱位。

原则3：若情形1、2均不存在，情形3存在，随机将必倒箱放入出现可能3情况的可行箱位。

原则4：若情形1～3均不存在，情形4存在，直接将必倒箱放入该可行箱位。

原则5：若情形1～4均不存在，情形5存在，找到出现情形5情况的各可行栈中的最大优先级别(数值最小)，组成一个集合，然后选择这个集合中优先级别最低(数值最大)的箱子所在的栈，放入必倒箱。

原则6：若情形1～5均不存在，情形6存在，直接将必倒箱放入该可行箱位。

3.2 启发式算法步骤

1)确定是否贝位内箱子都已被取走。若都已被取走，则取箱作业结束；若没有都被取走，转步骤2)。

2)确定待提箱及其所在栈和层，转步骤3)。

3)确定待提箱上方是否有压箱。若有压箱，则转步骤4)；若无压箱，即进行待提箱的取箱作业。

4)从待提箱最上方的压箱开始倒箱。找到所有的可行箱位，即不悬空并且不在待提箱所在栈的空箱位，转步骤5)。

5)遍历所有将倒箱放入可行箱位的情形，并且计算压箱量，转步骤6)。

6)运用基于6条倒箱落位原则进行倒箱落位决策，同时更新贝位状态，转步骤3)。

4 仿真算例与结果分析

4.1 算例1

如图5，贝位的初始堆放状态为3栈3层，其中有6个优先级别的箱子要按照它们的优先级别被取出。本例中预留了3个空箱位，完全满足初始堆垛对最少倒箱的要求。图中根据动态规划思想，列出了所有的链结构。通过比较，可以得出画线的方案是基于限制变量的类型方案的最优解，最终倒箱量为4。

仿真程序采用MATLAB7.9.0 R2009b 开发，所得结果在CoreTM2Duo,CPU2.00GHz,2.00GB内存平台下测得，见图6。

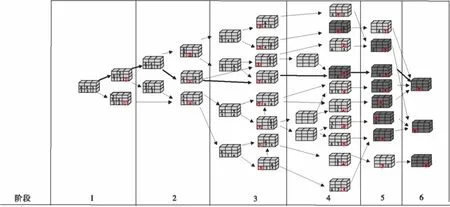
图5 仿真算例Fig.5 A sample of simulation

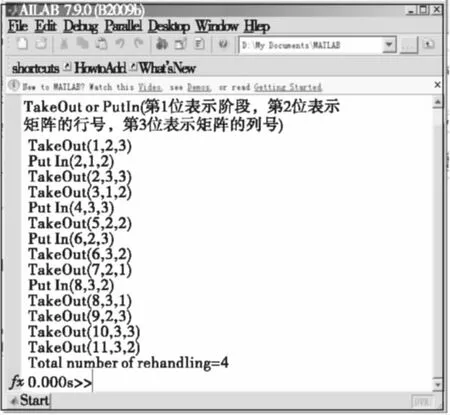
图6 MATLAB仿真结果Fig.6 Results of optimization via the software of MATLAB

MATLAB仿真结果和动态规划所得的最优解完全相同，计算时间非常短。若对图5和图6进行补充解释，则整个取箱过程异常清晰，先将(2,3)位置上优先级别为5的箱子TakeOut，然后PutIn到(1,2)；然后TakeOut(3,3)位置上的优先级别为1的箱子；紧接着是TakeOut(1,2)位置上优先级别为5的箱子PutIn到(3,3)位置上；然后TakeOut(2,2)位置上优先级别为4的箱子PutIn到(2,3)位置上；接着TakeOut(3,2)位置上优先级别为2的箱子；然后TakeOut(2,1)上优先级别为6的箱子PutIn倒(3,2)位置上；然后TakeOut(3,1)上优先级别为3的箱子；然后TakeOut(2,3)上优先级别为4的箱子，然后TakeOut(3,3)上优先级别为5的箱子；然后TakeOut(3,2)上优先级别为6的箱子。整个贝位取箱作业结束，总的倒箱量为4次；图5中颜色较深的贝位结构说明此阶段该贝位内没有倒箱作业；图5中运用动态规划所得的最优解的链结构已用颜色较深的箭头标出表明。仿真这个案例的同时，倒箱落位原则5得到证明，可以得到较优解。

4.2 算例2

针对更大规模的计算，文中所叙述的启发式算法经验证，均可得到较优解，算法的求解时间很短。因此再举一个6栈6层有25个箱子的初始贝位的算例，如图7。

图7 6栈6层的贝位初始状态Fig.7 Initial state of a bay with 6 stacks and 6 tiers

应用启发式算法求解后，得到的模拟结果是首先TakeOut(2,2)位置上优先级别为1的箱子；然后TakeOut(3,2)位置上优先级别为11的箱子，将之PutIn(2,5)的位置上；接着TakeOut(4,2)上优先级别为13的箱子，将之PutIn(2,4)的位置上；然后TakeOut(5,2)位置上优先级别是5的箱子，将之PutIn(1,5)位置上；然后TakeOut(6,2)位置上优先级别为2的箱子；然后TakeOut(4,1)上优先级别为12的箱子，将之PutIn(6,2)的位置上；然后TakeOut(5,1)上优先级别为3的箱子；然后TakeOut(4,3)上优先级别为14的箱子，将之PutIn(5,1)的位置；然后TakeOut(5,3)位置上优先级别为6的箱子，将之PutIn(4,1)位置上；然后将TakeOut(6,3)位置上优先级别为4的箱子；然后TakeOut(1,5)位置上优先级别为5的箱子；然后TakeOut(4,1)位置优先级别为6的箱子；然后TakeOut(2,4)位置上优先级别为13的箱子，将之PutIn(4,1)位置上；然后TakeOut(3,4)位置上优先级别为9的箱子，将之PutIn(3,1)位置上；然后TakeOut(4,4)位置上优先级别为7的箱子；然后TakeOut(2,5)位置上优先级别为11的箱子，将之PutIn(4,4)位置上；然后TakeOut(3,5)位置上优先级别为10的箱子，将之PutIn(5,2)位置上；然后TakeOut(4,5)位置上优先级别为8的箱子；然后TakeOut(3,1)位置上优先级别为9的箱子；然后TakeOut(5,2)位置上优先级别为10的箱子；然后TakeOut(4,4)位置上优先级别为11的箱子；然后TakeOut(6,2)位置上优先级别为12的箱子；然后TakeOut(4,1)位置上优先级别为13的箱子；然后TakeOut(5,1)位置上优先级别为14的箱子；然后TakeOut(6,1)位置上优先级别为15的箱子；然后TakeOut(5,4)位置上优先级别为16的箱子；然后TakeOut(5,5)位置上优先级别为17的箱子；然后TakeOut(6,4)位置上优先级别为18的箱子；然后TakeOut(6,5)位置上优先级别为19的箱子；然后TakeOut(1,6)位置上优先级别为20的箱子；然后TakeOut(2,6)位置上优先级别为22的箱子；然后PutIn(6,1)位置上；然后TakeOut(3,6)位置上优先级别为21的箱子；然后TakeOut(6,1)位置上优先级别为22的箱子；然后TakeOut(4,6)位置上优先级别为23的箱子；然后TakeOut(5,6)位置上优先级别为24的箱子；然后TakeOut(6,6)位置上优先级别为25的箱子；整个取箱过程结束。系统记录的完成时间仅仅为0.094s，总倒箱次数为11次。

5 结 语

以龙门吊起重机在贝位内取箱作业过程中倒箱量最少为目标，建立了龙门吊起重机取箱作业数学模型，使用MATLAB编译的启发式算法对数学模型进行求解。启发式算法基于6条倒箱落位原则，以整个取箱过程中倒箱数量最少为目标，每次的倒箱落位决策都基于二次倒箱数量最少。大量的随机生成不同规模的初始贝位状态，使用启发式算法进行仿真实验。

文中通过2个不同规模的算例进行了说明，算例1中贝位的初始堆放状态为3栈3层共6个箱子，经启发式算法求解得到的较优解与经动态规划求解得到的最优解相同；算例2中贝位的初始堆放状态为6栈6层共25个箱子，经启发式算法求解得到的较优解总倒箱量为11，求解时间为仅0.094 s。提高了取箱作业的效率，符合码头作业的时效性。因此验证了文中的取箱作业启发式算法提高了取箱作业的效率并且符合码头作业的时效性。

然而在配载图已知的情况下，对于出口箱而言，在堆场贝位内进行取箱作业，多个箱子的优先级别相同的情况是符合事实的。针对这种情况，基于相同的倒箱落位原则，笔者也设计了新的启发式算法，经验证效果也很好。实际上由于假设3的存在，注定了文中提出的启发式算法是属于贪心算法的范畴，求解得到的最优解可能不是整体最优解，因此下一步的研究将是非限制变量的类型方案。

[1] Kim K H.Evaluation of the number of re-handles in container yards [J].Computers and Industrial Engineering,1997,32(4):701-711.

[2] Kim K H,Park Y M,Ryu K R.Deriving decision rules to locate export containers in container yards [J].European Journal of Operational Research,2000,124(2):89-101.

[3] Kim K H,Hong G P.A heuristic rule for relocating blocks [J].Computers and Operations Research,2006,33(4):940-954.

[4] 张维英,林焰,纪卓尚,等.出口集装箱堆场取箱作业优化模型研究[J].武汉理工大学学报:交通科学与工程版,2006,30(2):314-317.Zhang Weiying,Lin Yan,Ji Zhuoshang,et al.Research of optimal formulation of retrieving operation of out-bounding containers in container port [J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2006,30(2):314-317.

[5] 白治江,王晓峰.集装箱翻箱优化方案设计[J].水运工程,2008(4):57-61.Bai Zhijiang,Wang Xiaofeng.Designation of reshuffling optimal solution of containers [J].Water Transportation Engineering,2008 (4):57-61.

[6] 李斌.基于动态规划的贝位内集装箱翻箱优化[D].大连:大连海事大学,2011.Li Bin.The Optimization Research for Container’s Upset Operation within A Container Bay through Dynamic Programming Method [D].Dalian:Dalian Maritime University,2011.

[7] 陈庆伟.基于遗传算法的堆场贝位分配优化问题研究[D].青岛：青岛大学,2007.Chen Qingwei.Research of Bay Allocation Optimization Problem in Terminal Yard based on Genetic Algorithm [D].Qingdao:Qingdao University,2007.

[8] 周留井.基于遗传算法的进口箱堆场贝位分配优化模型研究[D].广州：中山大学,2008.Zhou Liujing.Research of Bay Allocation Optimization Problem in In-Bounding Container Terminal Yard based on Genetic Algorithm [D].Guangzhou: Zhongshan University,2008.

[9] 金健.如何减少集装箱箱区两次翻箱[J].集装箱化,2002(1):42-43.Jing Jian.How to lower the second re-handling in container blocks [J].Containerized,2002(1):42-43.

[10] 金鹏,黄有方,严伟.位内集装箱翻箱操作的启发式优化[J].上海海事大学学报,2009, 30(4):13-16.Jing Peng,Huang Youfang,Yan Wei.Optimization of heuristic algorithm of container re-handling operation in bays [J].Journal of Shanghai Maritime University,2009,30(4):13-16.