FRP加固具单裂纹RC梁疲劳分析

刘 锋，陈得良

(1.长沙理工大学 土木与建筑学院，湖南 长沙 410014；2. 湖南大学 机械与运载工程学院，湖南 长沙 410082)

0 引 言

桥梁这类工程结构，常承受不同类型、不同重量和不同速度车辆的作用。RC(钢筋混凝土梁)梁在运营的过程中易产生裂纹，而FRP(纤维增强复合材料)具有质轻、高强、抗疲劳等特性，因此用FRP对该类带裂纹RC构件进行加固是桥梁加固的有效方法[1-3]。

FRP复合材料运用于桥梁加固的时间相对较短，现还鲜有关于FRP加固具单裂纹RC梁疲劳性能的研究报道。且现有的研究成果主要集中于实验研究。为了研究FRP加固RC梁后的疲劳性能，G.Williams，等[4]对加固后的Vintage桥进行了长期监控，并将数据与实验测试的结果进行对比研究。黄培彦，等[5-6]对FRP加固RC梁的疲劳主裂纹扩展速率和主裂纹的应力强度因子进行了相关研究。国内学者研究了CFL(碳纤维薄板)增强RC梁在循环载荷作用下的疲劳性能，并对其在随机变幅疲劳荷载下进行了相关实验研究[7-8]。裂纹导致的应力集中效应在国内外现有关于具单裂纹加固梁的研究还鲜有报道。在对具单裂纹加固梁进行疲劳分析时，笔者通过引入裂纹影响因子来描述裂纹尖端附近的应力集中现象，并结合加固梁对外载荷的位移响应，分析加固梁的疲劳性能。

1 动力学方程的建立

图1为FRP加固具单裂纹RC简支梁模型图，在梁上作用大小为Psinωt的简谐载荷，xC为裂纹距梁左端支座的距离，xP为载荷作用点距离梁左端支座的距离，AS1，AS2分别表示受压钢筋和受拉钢筋的截面面积,b表示梁宽的一半，d为梁高的一半，l表示梁的全长。

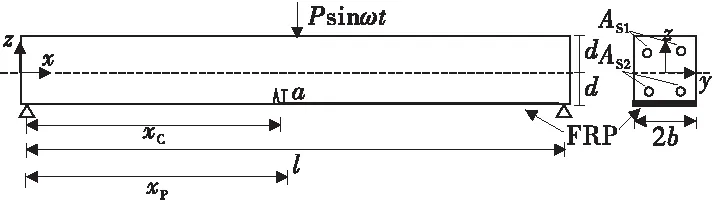
图1 FRP加固具单裂纹RC梁模型Fig.1 Model of cracked RC beam strengthened with FRP

FRP加固具单裂纹RC梁由混凝土、钢筋和FRP复合材料3种材料组成。为便于问题的研究，笔者将以上材料视为均质的弹性材料，并引入以下假设：

1)FRP上的应力不沿厚度方向发生变化[9]；

2)应变沿梁截面高度线性变化；

3)钢筋与混凝土、FRP与混凝土不产生相对滑移；

4)忽略梁的剪切效应以及黏结层的作用；

5)只研究裂纹发生较小扩展的情况。

基于以上假设，加固梁的位移模式可表示为：

(1)

(2)

式中:xC为裂纹的位置;a，d分别为裂纹的深度和梁高的1/2;α为裂纹沿尖端应力的衰减率,本模型中α=1.276[11]；m为应力沿横向线性变化的斜率。

对于不超过中性轴的微小裂纹，加固梁中性轴以上的应力、应变可以忽略裂纹对其的影响，其中Heaviside 函数u(d-a-z)为：

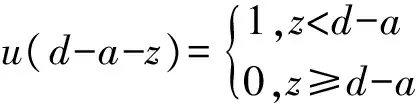
(3)

通过Hamilton能量变分原理，具单裂纹加固梁的动力学方程为：

(4)

式中：T，U和V分别为系统的动能、应变能和外力势能;δ为变分符号;t为时间变量。

混凝土、钢筋和FRP的动能分别为：

(5)

(6)

(7)

式中：ρC，ρS，ρF分别为混凝土、钢筋和FRP的密度；AC为混凝土梁截面面积；AS1，AS2分别为受压钢筋和受拉钢筋的截面面积；AF为FRP截面面积；VC，VS，VF分别为混凝土梁、钢筋和FRP的体积。

对于细长梁，式(5)～式(7)的第二项可以忽略不计，对式(5)～式(7)沿截面高度积分可得：

(8)

含单裂纹混凝土梁、钢筋和FRP的应变能分别为：

(9)

(10)

(11)

将式(1)代入式(9)～式(11),并沿截面积分，得：

(12)

式中：EC，ES，EF分别为混凝土、钢筋和FRP的弹性模量，其中：

(13)

式中：zSi(i=1,2)，zF分别为中性轴到钢筋和FRP形心的距离。

加固梁总的动能和应变能为：

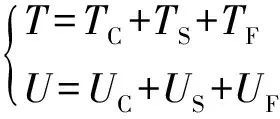
(14)

加固梁的外力势能V为：

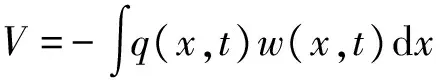
(15)

式中：q(x,t)为分布荷载，简介q。

将方程(14)和方程(15)代入方程(4)，可得：

(16)

对式(16)进行分部积分后可得：

(17)

简支梁的边界条件为：在x=0 和x=l处δw=0，δw″=0。

根据分离变量法，假设式(17)的解为：

w=W(x)T(t)

(18)

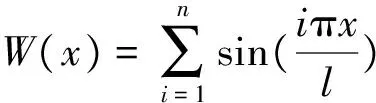
(19)

将式(18)和式(19)代入式(17)，可得：

(20)

式中：α1=ECf(x)+ES[fS1(x)+fS2(x)]+EFfF(x)；α2=ρCAC+ρS(AS1+AS2)+ρFAF。

(21)

整理后为：

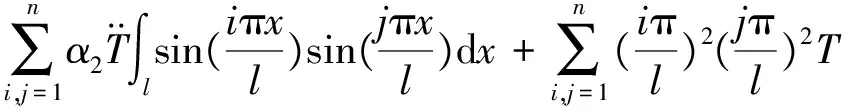
(22)

将式(22)写成矩阵的形式：

(23)

式中：T=[T1,T2,…,Tn]T为n阶列向量。

质量矩阵M、刚度矩阵K和广义力矩阵Q可以写成：

(24)

(25)

(26)

式中：[I] 为n×n单位矩阵。

2 疲劳寿命计算公式推导

现有研究成果表明，当FRP加固RC梁发生以钢筋疲劳断裂为主导的破坏方式时，能最大限度地发挥加固梁上各材料的材料性能[12]。因此，笔者对加固梁进行疲劳性能分析也是基于此种破坏方式。现假设当加固梁的裂纹扩展到一定的深度时，由于刚度的减小梁会产生较大的变形，随即钢筋相继发生脆性断裂，同时加固梁完全丧失承载能力。

根据材料力学的相关知识，加固梁上任意一点的应变可表示为：

(27)

式中：Ei和Ii分别表示弹性模量和惯性矩；i=C、S1、S2、F分别表示混凝土、受压钢筋、受拉钢筋和FRP；M为点所在截面处的弯矩；y为中性轴到所要计算应变点的距离。

因此，梁上任意一处的应力可表示为：

(28)

加固梁上任意一处弯矩的大小可表示为：

M=∑EiIiw″

(29)

将式(29)代入式(28)可得：

σC=ECyw″

(30)

将FRP加固具单裂纹RC梁在Psinωt作用下的位移响应式(18)代入式(30)可得:

(31)

根据断裂力学的相关理论，加固梁裂纹处的裂纹应力强度因子可表示为：

(32)

式中：F(ξ)为是应力强度因子修正系数[13]，其与梁的形状、加载方式和边界条件有关，且

F(ξ)=1.017-2.120ξ+7.710ξ2-13.55ξ3+14.25ξ4

(33)

式中：ξ=a/h；a为裂纹长度；h为梁的高度。

将式(31)代入式(32)可得：

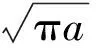
(34)

根据相关疲劳裂纹扩展速率研究成果，假设加固梁疲劳主裂纹的稳定扩展速率为da/dN，通过Paris-Erdogan方法，其可以表示为：

(35)

式中：C和m为材料常数，C=0.902，m=5.74[13]。

故，式(35)可表示为：

(36)

式中：ΔK为梁在最大交变应力σmax和最小交变应力σmin时计算得到的应力强度因子值之差：

ΔK=Kmax-Kmin

(37)

对式(36)进行积分可计算出加固梁的疲劳寿命：

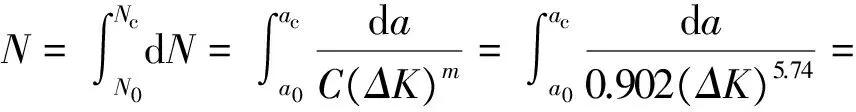
(38)

式中：a0为裂纹的初始长度；aC为裂纹临界长度；N0为a0时载荷作用的周期数；NC为aC时载荷作用的周期数。

为了提高计算精度，现将初始裂纹到临界裂纹的长度平均划分成m段，即：

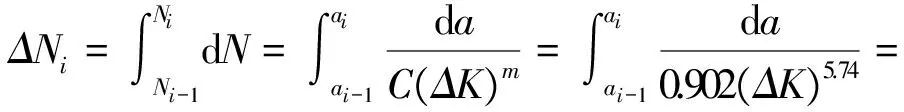
(39)

故加固梁总的疲劳寿命为：

(40)

3 数值分析结果与讨论

图1中FRP加固具单裂纹RC简支梁在简谐荷载作用下模型的参数如表1。

表1模型的参数Table 1 Parameters of modeling

将理论计算结果与有限元计算结果进行对比。为了准确模拟裂纹对梁的影响，梁用SOLID95单元模拟，钢筋用LINK8单元模拟，而FRP片材用SHELL63单元模拟。ANSYS模型未考虑钢筋与混凝土、FRP与混凝土间的滑移，同时忽略黏结层的作用。

3.1 加固梁应力强度因子分析

图2为加固梁在跨中分别作用频率为ω=10 Hz，大小为P=1，2，3 kN的正弦载荷时，理论计算与数值模拟的应力强度因子与裂纹深度关系曲线对比图。

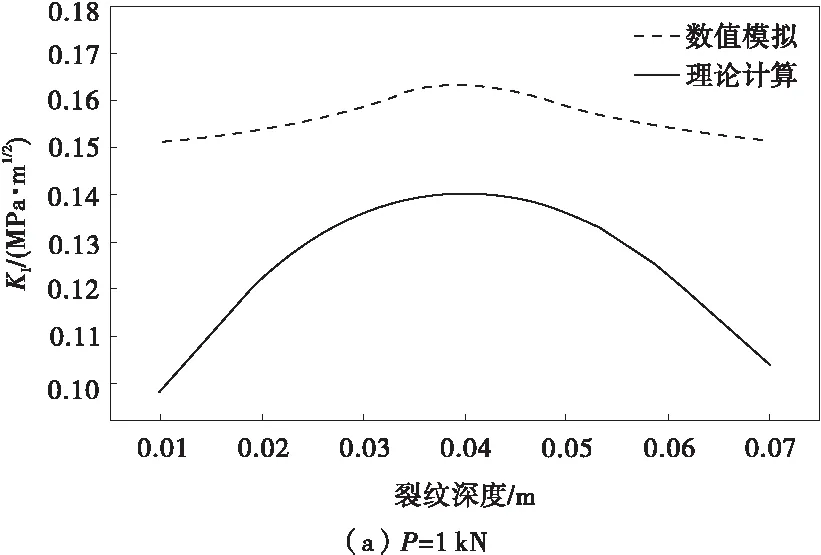
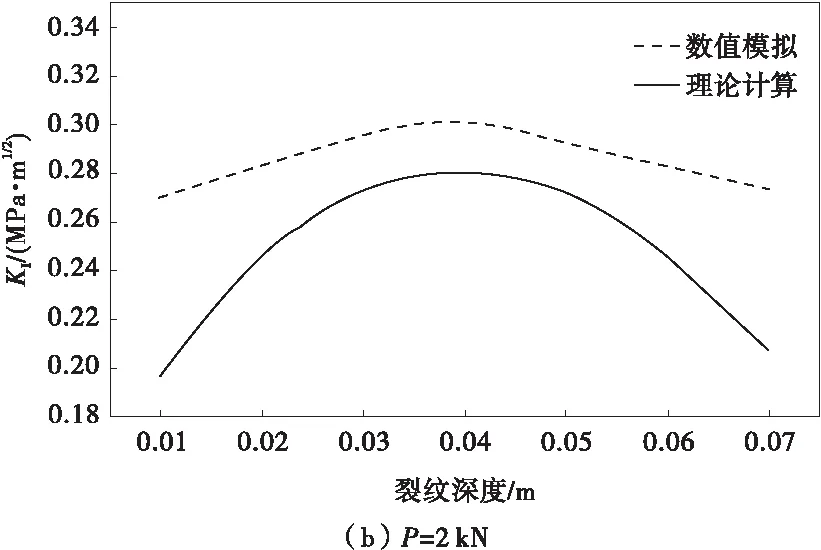
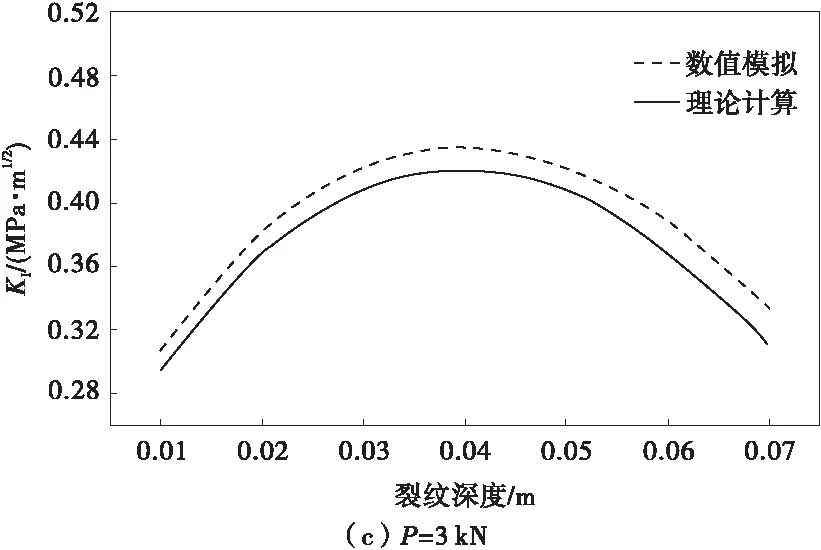
图2 不同方法分析的应力强度因子与裂纹深度的关系曲线Fig.2 Relation curve of stress intensity factor and crack depth analyzed by different methods

从图2可看出，与数值模拟的结果相比理论计算的应力强度相对较小，但两者具有相同的变化趋势；当a=0.04 m时两种方法计算的应力强度因子均达到最大值，而当a>0.04 m时，两种方法计算的应力强度因子均随裂纹深度的增加而减小，这是因为随着裂纹不断扩展，FRP复合材料将逐渐发挥其对梁的加固作用；当施加的载荷较大时，两种方法计算的结果吻合得较好。

3.2 加固梁疲劳主裂纹扩展寿命分析

图3为加固梁在跨中分别作用频率为ω=10 Hz，大小为P=1，2，3 kN的正弦载荷时，理论计算与数值模拟加固梁疲劳主裂纹扩展寿命预测值曲线。

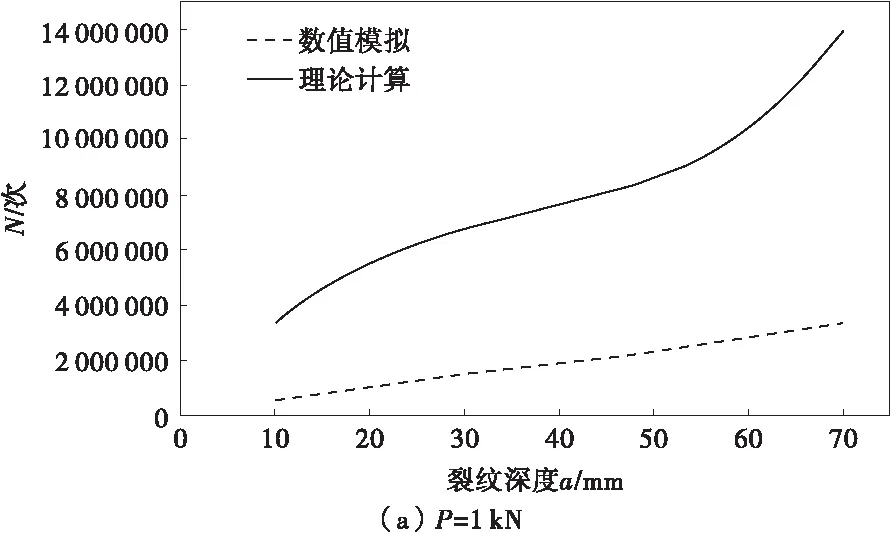
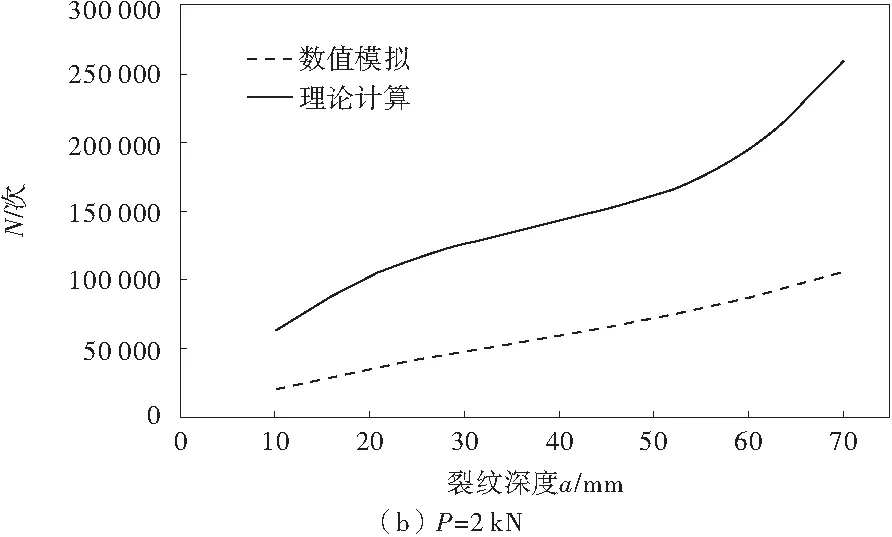
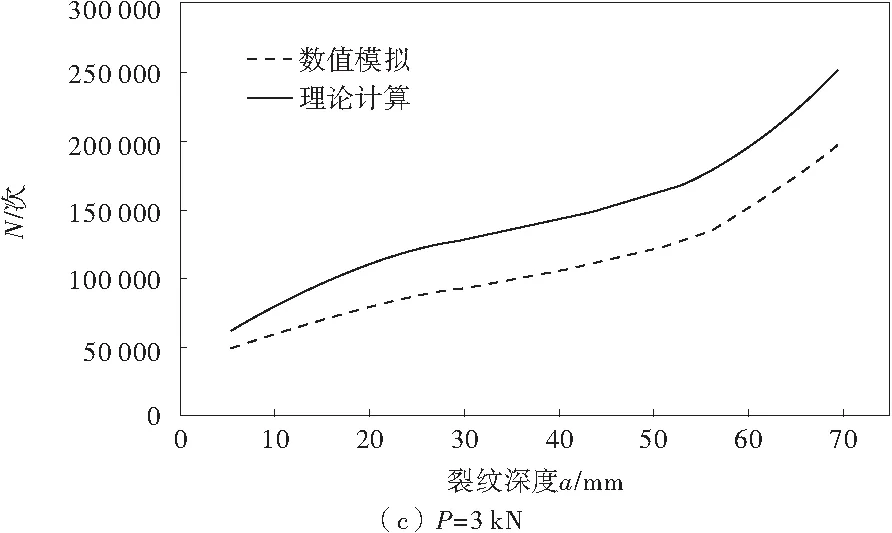
图3 不同方法分析的疲劳主裂纹扩展寿命与裂纹深度的关系曲线Fig.3 Relation curve of fatigue life of crack propagation and crack depth analyzed by different methods

从图3可看出，对加固梁疲劳主裂纹扩展寿命进行计算时，理论计算的结果与数值模拟的结果变化趋势相一致，但数值模拟的结果较理论值小；加固梁在较小的载荷作用时，两种方法计算的结果差值较大，而当加固梁所受到的载荷较大时，理论值与数值模拟的结果吻合的较好；同时随着裂纹深度的增加，理论值与数值模拟结果的差值逐渐增大。

4 结 论

为研究FRP加固具单裂纹RC梁在循环载荷作用下的疲劳主裂纹扩展寿命，笔者先求出加固梁对载荷的位移响应，再运用材料力学和断裂力学的相关理论计算裂纹的应力强度因子，最后采用Paris-Erdogan方法对加固梁进行疲劳寿命分析，并将该种方法计算的结果与有限元模拟的结果进行了对比。通过分析得出了以下结论：

1)裂纹尖端处的应力强度因子随裂纹深度的增加呈现先上升后下降的变化趋势，且随载荷的增加逐渐变大。

2)加固梁的疲劳寿命对载荷的变化较为敏感。加固梁的疲劳剩余寿命随着裂纹的扩展先缓慢减少，而当a>0.15 m时裂纹梁的疲劳剩余寿命加速减少，当a>0.55 m时梁的疲劳主裂纹扩展寿命曲线变缓。

3)对加固梁进行应力强度因子计算时，数值模拟的结果与理论方法计算的结果具有相同的变化趋势，但理论值均小于数值模拟的结果。当加固梁受到较大的载荷作用时，两者的计算结果吻合得较好。

4)对加固梁进行疲劳主裂纹扩展寿命分析时，理论值与数值模拟的结果具有相同的变化趋势，但数值模拟的结果较理论值小。

[1] 王作虎,刘晶波,杜修力.FRP加固钢筋混凝土结构尺寸效应的研究进展[J].建筑科学与工程学报,2011,28(3)：45-55.

Wang Zuohu,Liu Jingbo,Du Xiuli.Research progress of size effect on reinforced concrete structures strengthened with FRP[J].Journal of Architecture and Civil Engineering,2011,28(3):45-55.

[2] Heffernan P J,Erki M A.Fatigue behavior of reinforced concrete beams strengthened with carbon fiber reinfoeced plastic laminates[J].Journal of Composites for Construction,2004,8(2):132-140.

[3] Wu Z J,Bailey C G,Fracture resistance of a cracked concrete beam post-strengthened with FRP sheets[J].International Journal of Fracture,2005,135:35-49.

[4] Williams G,Higgins C,ASCE P E M.Fatigue of diagonally cracked RC girders repaired with CFRP[J].Journal of Bridge Engineering,2008,13(1):24-33.

[5] 黄培彦,刘健,郭馨艳,等.FRP加固RC梁疲劳主裂纹扩展速率研究[C]//中国力学学会学术大会2009论文摘要集.北京：中国力学学会，2009:1-6.

Huang Peiyan,Liu Jian,Guo Xinyan,et al.Study on fatigue crack propagation rate of RC beams strengthened with fiber reinforced polymer [C]// Proceedings of the 2009 Chinese Society of Theoretical and Applied Mechanics Academic Conference.Beijing:Chinese Society of Theoretical and Applied Mechanics,2009:1-6.

[6] 黄培彦,吴承华,郑小红,等.FRP加固RC梁主裂纹的应力强度因子[C]// 第十四届全国疲劳与断裂学术会议论文集.北京：中国机械工程学会，2008:1811-1814.

Huang Peiyan,Wu Chenghua,Zheng Xiaohong,et al.Stress intensity factor of the main crack in RC beam strengthened with FRP[C] //Proceedings of the 14th National Conference on Fatigue and Fracture.Beijing:Chinese Mechanical Engineering Society,2008:1811-1814.

[7] 姚国文,黄培彦.循环载荷下纤维薄板增强板RC梁的疲劳性能研究[J].土木工程学报,2006 ,39(4):35-38.

Yao Guowen,Huang Peiyan.A study on the fatigue behavior of RC

beam strengthened with fiber laminates[J].China Civil Engineering Journal,2006,39(4):35-38.

[8] 韩强,黄培彦,赵琛,等.随机变幅疲劳荷载下CFL增强RC梁疲劳寿命的试验研究[J].建筑技术,2009,40(4):317-320.

Han Qiang,Huang Peiyan,Zhao Chen,et al.Experimental study on fatigue life of RC beams strengthened with CFL under random-amplitude fatigue load[J].Architecture Technology,2009,40(4):317-320.

[9] Wu Zhishen,Niu Hedong.Study on debonding failure load of RC beams strengthened with FRP sheets[J].Journal of Structural Engineering,2000,46(A):1431-1441.

[10] Christides S,Barr A D S.One-dimensional theory of cracked Bernoulli-Euler beams[J].International Journal of Mechanical Sciences,1984,26:639-648.

[11] Shen M H H,Pierre C.Free vibrations of beams with a single-edge crack[J].Journal of Sound and Vibration,1994,170(2):237-259.

[12] 汪镇江.FRP加固RC疲劳性能研究[D].北京:北京交通大学,2006:13-15.

Wang Zhenjiang.Study on the Fatigue Characteristics of RC Beam Strengthened with FRP[D].Beijing:Beijing Jiaotong University,2006:13-15.

[13] Huang Peiyan,Liu Guangwan,Guo Xinyan,et al.Experimental study on the fatigue crack propagation rate of RC beam strengthened with carbon fiber laminat[C] // Proceedings of the International Society for Optical Engineering.Nanjing:The International Society for Optical,2008.