钢箱混凝土组合拱桥施工过程中温度效应分析
韩 辉,吕 娜,周志祥,张 金
(1.重庆市公路局,重庆 401147;2.重庆交通大学 土木建筑学院,重庆 400074)
常规混凝土拱桥经济适用,美观耐久,养护维修费用低,是跨越山区深谷的理想桥型,但是传统的通过预制-吊装形成的混凝土箱板拱桥在主拱形成期间的结构稳定性差,施工风险大;拱箱节段的预制-运输-安装对场地和设备要求高。周志祥,等[1-2]将钢混凝土组合结构和拱桥结合,提出了钢箱-混凝土组合拱桥,并对其施工过程和运营过程中的力学行为进行了多方面深入研究,已应用于多座桥梁建设中。
钢-混凝土组合结构桥梁由于钢箱与混凝土两种材料热传导性能不同,各自受温度的影响不同,在季节整体温度变化及日照温度作用下,其内部将不可避免的产生相应的应力重分布及结构变形,这种特性一直为钢-混凝土组合结构研究工作者所关注。目前对于钢管混凝土拱桥研究最为深入,在系统温变[3]、日照温变[4]等方面均有所研究。研究表明,钢管混凝土拱桥受温度影响显著[5],设计时不可忽略。
钢箱混凝土组合拱桥在施工过程中,主拱截面从空钢箱变化成为分段不同形式的钢-混凝土组合截面,温度变化对主拱受力的过程较为复杂,笔者将从整体温变作用(陡变温差)的角度着手,在钢箱混凝土拱桥主拱结构施工过程中,对各施工阶段主拱结构在均匀升降温情况下的受力性能的变化进行分析;分析日照温度荷载使主拱结构形成的不同瞬时温度场。上述分析将得到整体温变作用及日照作用下主拱不同阶段的温度效应。
1 工程结构温度计算理论
工程温度荷载分析,目前普遍利用傅里叶热传导方程求解[6]。
在某一时刻,工程结构上某一点的温度Ti可用式(1)表示:
Ti=f(x,y,z,t)
(1)
可导出对于匀质、各向同性的材料,三维不稳定热导方程:
(2)
式中:λ为热传导系数;c为混凝土比热;γ为混凝土容重。
热传导方程是物体的温度与时间和空间的关系,为求得工程上的唯一解,要找出符合方程的初始条件与边界[7]。初始条件为结构初始时刻即t=0时的温度条件,边界条件是结构边界上的温度分布状况或者热交换状况。
1.1 初始条件
一般选择在结构整体温度分布较均匀的时刻。当t=0时:
T0=(x,y,z,0)=K
(3)
式中:K为常数。
1.2 边界条件
第1类:固体表面温度为已知的时间函数:
T(t)=f(t)
(4)
第2类:固体表面热流密度为已知函数:
(5)
式中:n为表面外法线方向。
若材料绝缘,有:
(6)
第3类:当固体与流体(主要为空气)接触时,在固体表面的热流密度与固体表面温度T和空气温度Ta之差成正比:
(7)
式中:β为表面放热系数。
第4类:不同的两种固体接触良好,则在接触面上温度与热流密度连续:
(8)
式中:T1,T2分别为两种固体的表面温度;k1,k2分别为两种固体的热导系数。
若两种固体接触不良,则温度不连续,T1≠T2,此时需引入接触热阻。
2 工程案例
重庆江津笋溪河大桥主桥为净跨100 m的钢箱-混凝土组合拱桥,桥梁全长163.90 m,腹孔和引桥的标准跨径为8.8 m,上承式受力,矢跨比为1/7.143,拱轴系数为2.240。桥梁宽度为7 m(行车道)+2×1.5 m(人行道)+2×0.25 m(人行道栏杆)=10.50 m,汽车设计荷载为公路-Ⅱ级,人群荷载为2.5 kN/m2。江津笋溪河大桥总体布置及主拱典型截面分别见图1、图2。
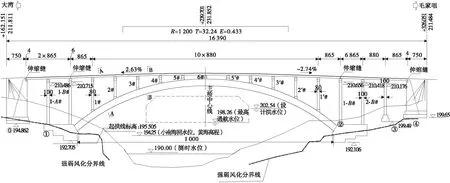
图1 江津笋溪河大桥总体布置Fig.1 General layout of Sunxi River bridge, Jiangjin
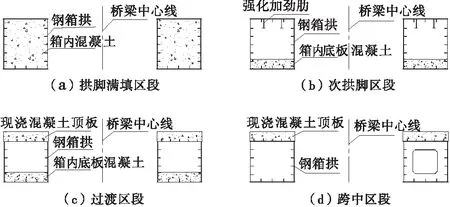
图2 江津笋溪河大桥主拱典型截面Fig.2 Typical sections of Sunxi River bridge’s main arch
桥位处于亚热带季风性湿润气候,年平均气候在18 ℃左右,冬季最低气温平均在6~8 ℃,夏季较热,七、八月日最高气温均在35 ℃以上。极端气温最高41.9 ℃,最低-1.7 ℃,日照总时数1 000~ 1 200 h,大桥主拱结构,在日照作用下,主拱结构顶面及外表面直接受日照的作用,而结构底面及内侧面并没有直接受日照的作用。由此产生的温差变化在桥梁建设时要加以考虑。
3 主拱基于温变有限元模型的建立
3.1 整体温变在主拱施工各阶段中的影响
假定:①浇筑混凝土阶段,拱肋混凝土收缩徐变、环境的温度影响不予考虑;②各材料均为连续、均质、各向同性、完全弹性的。
根据工程概况中相关信息,按照实际结构尺寸,利用有限元软件ABAQUS建立半跨单片拱肋的模型(两片对称)(图3),考虑了主拱钢箱、满填混凝土、箱内隔板混凝土、顶底板混凝土以及加劲肋、横隔板等构造措施的作用。

图3 有限元计算模型Fig.3 The FEA model
有限元模型中混凝土采用三维实体单元,钢箱、横隔板等采用三维壳单元,两侧拱脚处施加固端约束。
3.2 日照温度对成桥后主拱的影响
1)结合温度场分析理论[8],根据以往研究钢管混凝土结构断面温度场分布[9]的资料,初始条件选择6:30时刻结构截面的温度分布。
2)根据文献[10],气温的日变化可近似地在日最高气温和日最低气温之间按照正弦函数变化:
(9)
式中:Tmax为日最高气温;Tmin为日最低气温;t为时刻。
3)根据欧洲洲规范[11]计算得出混凝土热传导系数为λ=1.92 W/(m·K);混凝土的比热为c=913 J/(kg·K);混凝土表面的综合辐射系数取0.7。 直接受日照作用的结构顶面及外表面对流换热系数采用:
α=3.83w+4.67
生机勃勃的春天来了。春姑娘迎着春风,踏着轻盈的脚步款款而来,她用温柔的声音唤醒了校园里的万物。柳树姑娘梳理着长长的辫子;小草弟弟探出了头,好奇地打量着这个世界;迎春花姑娘绽开了笑脸,向春姑娘打着招呼;溪流冲破了层层阻碍,一路唱着欢乐的歌。校园里处处绿意盎然,仿佛穿上了一件绿色的新装。
(10)
没有直接受日照作用的结构底面及内侧面对流换热系数采用:
α=3.83w+2.17
(11)
式中:w为当地该时刻风速,m/s。
根据式(10)与式(11)确定结构顶面及外表面对流换热系数为α=8.5 W/(m·℃);结构底面及内侧面对流换热系数α=6 W/(m·℃)。
4 温变作用分析
4.1 整体温变作用对施工阶段主拱的影响
考虑空钢箱阶段及主拱成型阶段整体温变作用[12],假设每个阶段所处状态温度均为20 ℃,在均匀升降温5,10,15,20 ℃时,分别分析各阶段主拱结构在均匀升降温情况下的受力性能变化。
4.1.1 空钢箱拱阶段整体温变作用影响
1)主拱结构竖向变形分析
图4为整体温变作用对钢箱拱竖向变形的影响。由图4可知,空钢箱阶段均匀温变作用下,主拱结构各点均发生竖向变形,基本上与温度成正比,且从拱脚往跨中逐渐增大,最大跨中变形达45 mm。
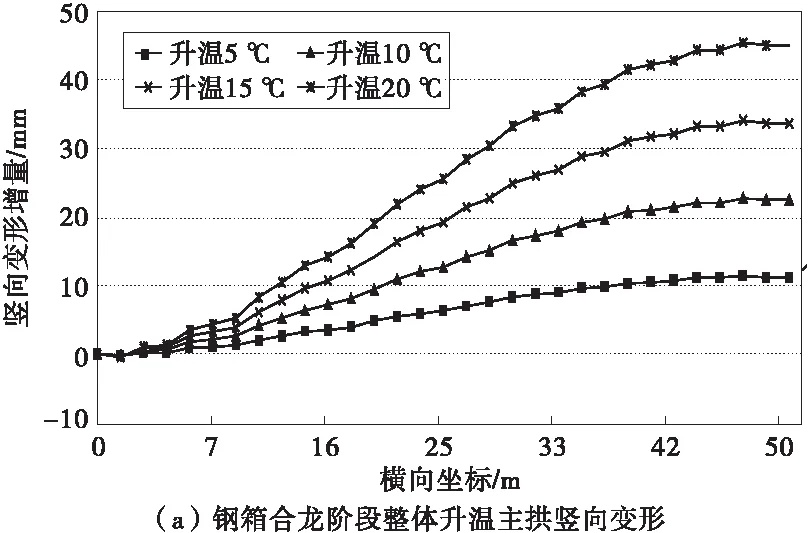
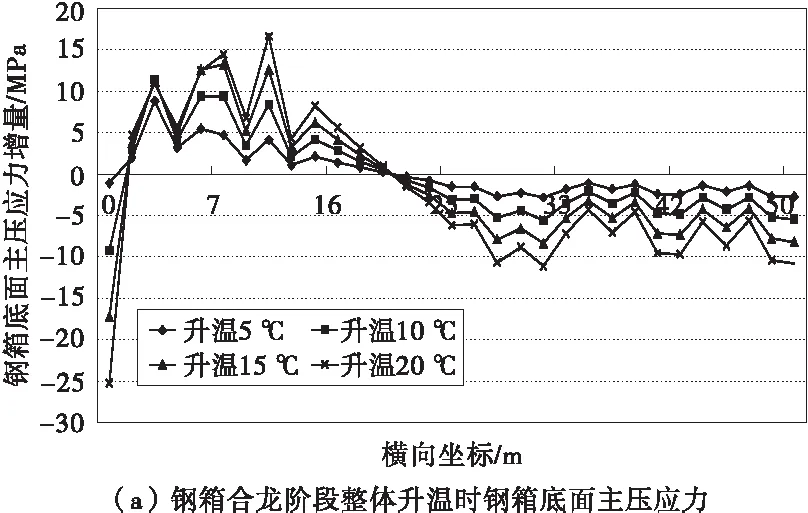
图4 整体温变作用对钢箱拱竖向变形的影响Fig.4 Influence of temperature change on vertical deformation of steel box arch
2)主拱钢箱底面主压应力对比分析
图5为温变作用对钢箱拱底面主压应力的影响。由图5可知,空钢箱阶段均匀升温引起拱脚、次拱脚区段钢箱底面受拉,引起过渡区段、跨中区段钢箱底面受压;均匀降温引起拱脚、次拱脚区段钢箱底面受压,过渡区段、跨中区段钢箱底面受拉。拱脚处钢箱底面各点主应力逐级积累,最大累计增量达到40 MPa。


图5 温变作用对钢箱拱底面主压应力的影响Fig.5 Influence of temperature change on principal compressive stress of steel-box arch bottom
4.1.2 组合拱主拱成拱阶段整体温变作用影响
1)主拱结构竖向变形分析
图6为整体温变对钢箱-混凝土组合拱竖向变形的影响。由图6可知,主拱成拱阶段均匀温变作用下主拱结构各点均发生竖向变形,与温度基本上成正比,且从拱脚往跨中逐渐增大,跨中最大变形达39 mm。

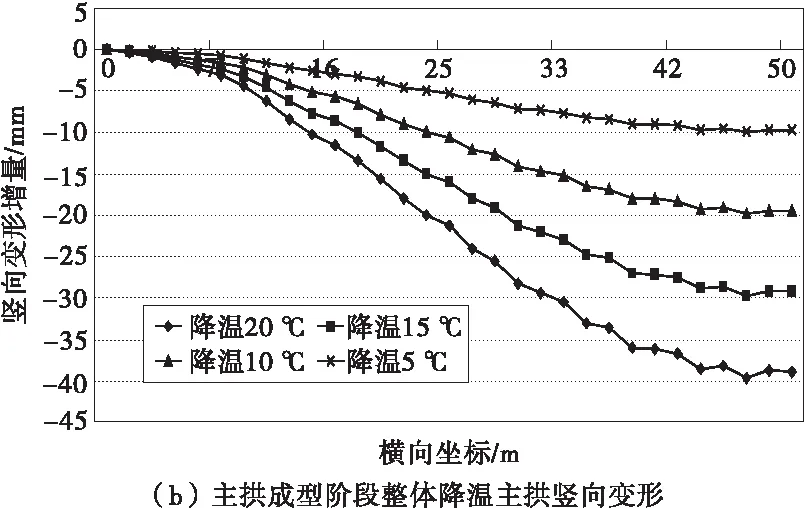
图6 结构整体温度变化对钢箱-混凝土组合拱竖向变形的影响Fig.6 Effect of overall temperature change on vertical deformation
2)主拱钢箱底面主压应力对比
图7为整体温变对钢箱-混凝土组合拱钢箱底面主压应力的影响。图7表明温度均匀升高使拱脚、次拱脚区段钢箱底面受到拉力作用,使过渡区段、跨中区段钢箱底面受到压力作用;而温度均匀降低对相应区段的影响则相反。主拱3/8L处钢箱底面各点主应力逐级积累,最大累计增量达到25 MPa。


图7 整体温度变化对钢箱底面主压应力的影响Fig.7 Effect of overall temperature on principal compressive stress of steel-box bottom
4.1.3 温度影响对比
1)刚度对比
表1为空钢箱拱与钢箱-混凝土组合拱温度影响下最大变形对比。

表1 温度影响下最大变形Table 1 Maximum deformation under temperature influence /mm
2)应力对比
表2为空钢箱拱与钢箱-混凝土组合拱温度影响下最大应力累积对比。

表2 温度影响下最大应力累积Table 2 Maximum stress accumulated under temperature influence /MPa
由表1、表2可见,空钢箱阶段升降温最大变形45 mm,主拱成型阶段升降温最大变形40 mm左右,主拱各阶段变形与温度基本上成线性关系;空钢箱阶段升温引起最大应力25 MPa,降温引起最大应力40 MPa,均发生在拱脚处;主拱成型阶段升温引起最大应力25 MPa,降温引起最大应力15 MPa,均发生在约3/8L处。可以得出,钢箱-混凝土主拱内混凝土对于增加主拱刚度,改善整体温变作用下结构受力有较显著作用。
4.2 主拱日照温度场分析
针对合龙后主拱拱脚满填混凝土区段、次拱脚区段及跨中区段的日照温度场情况,进行了主要截面温度场模型分析。温度场分析模型计算以夏季07:00时截面分布温度20 ℃作为初始边界条件,以19:00作为计算的终点状态,计算截面12 h后的瞬态温度分布。
4.2.1 拱脚区段截面温度场分析
图8为12 h后的结构断面温度云图。

图8 12 h后的结构断面温度云图Fig.8 12 h-later temperature nephogram of cross section
由图8可看出,拱脚区段截面的温度场在经过12 h日照后钢箱表面与内部混凝土温度有较大差异。日落时,大部分核心混凝土的温度仍维持在20 ℃,且因日照作用面不同,截面温度呈不对称分布。
图9为日最高温度15:00时刻拱脚区段钢箱顶底面及左右侧面温度分布柱形图。由图9可以看出:钢箱表面四周的温度分布不均匀,最大温度差值为:钢箱顶面1.4 ℃,底面2 ℃,左侧面1.45 ℃,右侧面1.96 ℃;在钢箱每个面的4个角部位温度相对较高,而较大部分中间区域温度相对低,而中间区域是钢箱与混凝土结合区域最大的地方。
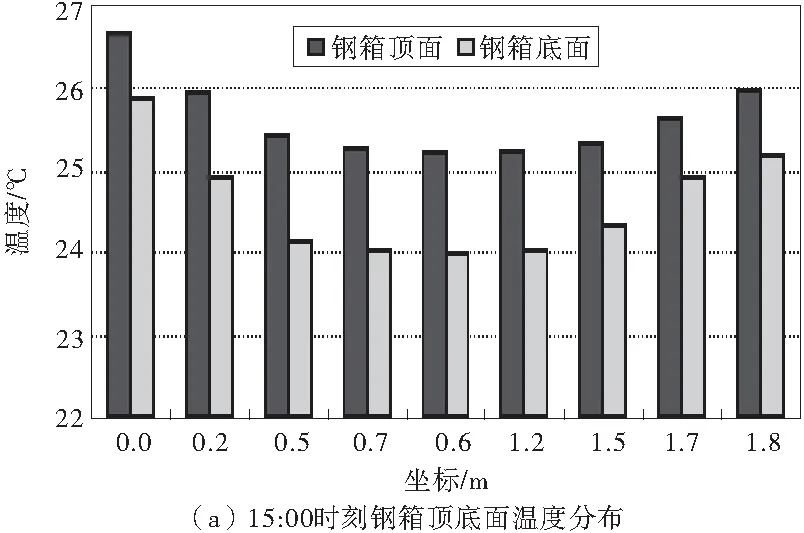

图9 典型时刻钢箱表面温度分布Fig.9 Temperature of steel box surface at typical moment
4.2.2 次拱脚区段截面温度场分析
图10为日照12 h后为箱内底板混凝土的温度场分布,从周围往中间使混凝土温度逐渐扩散升高,但扩散区域不大,到日落时间时,绝大部分核心混凝土的温度仍为20 ℃。

图10 次拱脚区段12 h后的结构截面温度云图Fig.10 Temperature nephogram of arch foot section after 12 h
图11为15:00时刻拱脚区段钢箱表面温度分布柱状图形。由图11可知,钢箱表面温度都不尽相同。钢箱顶面的温度分布均匀,维持在33 ℃左右。钢箱左右侧面的温度较一致从33 ℃左右缓慢降至28 ℃附近,钢箱底面的温度从两端往中间区域逐渐降低,但幅度不超过3 ℃。
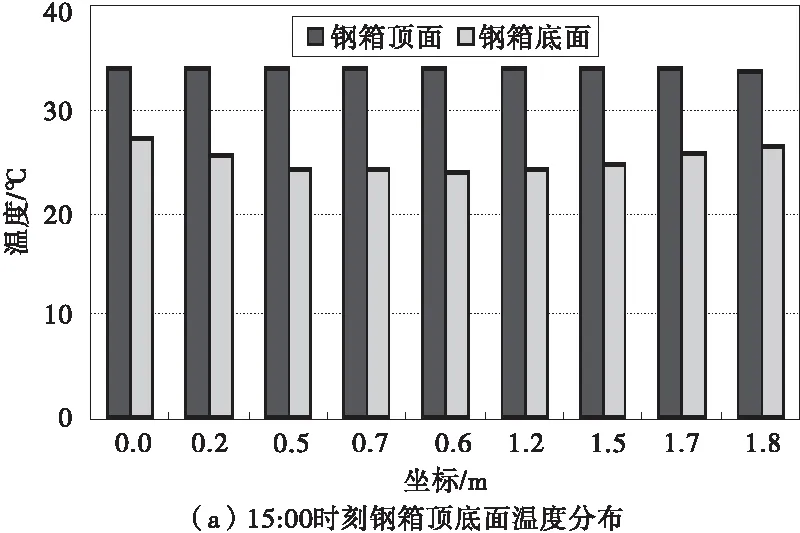

图11 典型时刻钢箱表面温度分布Fig.11 Temperature of steel box surface at typical moment
4.2.3 跨中区段截面温度场分析
图12 为12 h后的结构断面温度云图。从图12中可以看出,箱顶顶板混凝土的温度场分布在一天之中从四周往中间逐渐扩散升高,到日落时,大部分核心混凝土的温度仍然维持在20 ℃,且因日照作用面不同,截面温度呈不对称分布。

图12 跨中区段12 h后的结构断面温度云图Fig.12 Temperature nephogram of cross section after 12 h
图13为在一天之中温度最高时刻15:00时过渡区段钢箱顶底面及左右侧面温度分布图。由图13可以看出,钢箱顶面的温度分布大致从两端往中间区域逐渐降低,变化幅度大致有10 ℃,底面温度分布均匀,维持在34 ℃左右,钢箱左右侧面的温度变化基本一致,从中间区域往两端逐渐降低,变化幅度在5 ℃左右。
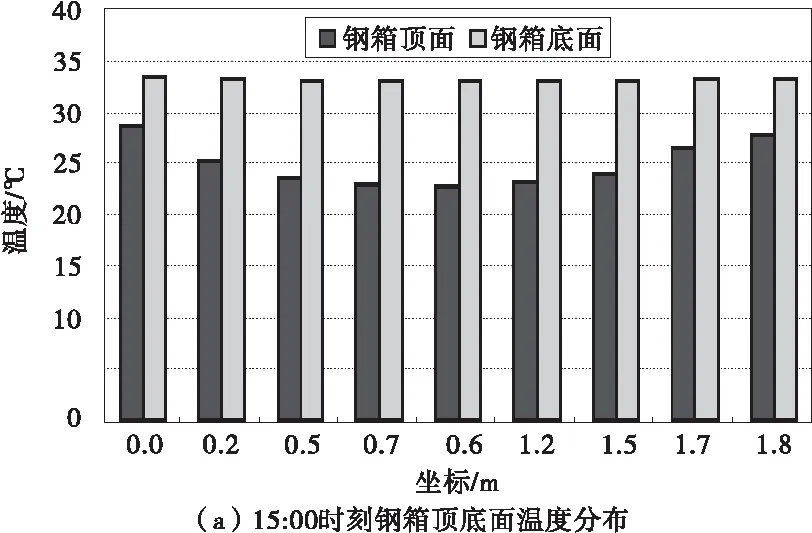

图13 典型时刻钢箱表面温度分布Fig.13 Temperature of steel box surface at typical moment
由日照温变作用下的钢箱-混凝土组合截面温度场分布研究表明:由于内部混凝土的传热性能低于钢材,使得组合截面内部和外部在日照时和日照后均有差异,内部混凝土在升温和降温过程中的温度变形均慢于钢箱,这有利于缓和由于日照影响产生的钢箱-混凝土组合拱桥不同截面温度差及由此产生的不均匀受力变形。
5 结 论
1)主拱结构在均匀升降温20 ℃作用下,空钢箱阶段升降温最大变形为45 mm,主拱成型阶段升降温最大变形为40 mm,主拱各阶段变形与温度基本上成线性关系;空钢箱阶段升温引起最大应力25 MPa,降温引起最大应力40 MPa,均发生在拱脚处;主拱成型阶段升温引起最大应力25 MPa,降温引起最大应力15 MPa,均发生在约3/8L处。结果表明:整体温度变化对钢箱-混凝土组合拱桥施工过程的影响不可忽略,且对空钢箱拱阶段的影响大于钢-混凝土组合拱成型阶段。
2)在日照温度变化作用下,钢箱-混凝土组合截面将会产生箱内箱外及各表面间的温度场差异。由于内部混凝土的传热性能远低于表面钢材,在日照作用下核心混凝土温度相对于初始状态几乎没有变化,这有利于缓和由于日照影响产生的钢箱-混凝土组合拱桥不同截面温度差及由此产生的不均匀受力变形。
[1] 周志祥,徐勇,吴海军.一种竖转钢-混凝土组合拱桥:中国,ZL200710048919.8 [P].2008-11-26.
Zhou Zhixiang,Xu Yong,Wu Haijun.A Vertical Transfer of Steel - Concrete Composite Arch Bridge:China,ZL200710048919.8[P].2008-11-26.
[2] Zhou Zhixiang,Fan Liang,Wang Shaorui,et al.Chongqing Wansheng Zaodu bridge-steel box-concrete composite arch bridge[J].Structure Engineering International,2013,23(1):71-74.
[3] 李自林,刘明艳,李妲.大跨度钢管混凝土拱桥温度效应研究[J].铁道建筑,2010 (8):18-20.
Li Zilin,Liu Mingyan,Li Da.Span CFST arch temperature effect research [J].Railway Engineering,2010 (8):18-20.
[4] 孙国富.大跨度钢管混凝土拱桥日照温度效应理论及应用研究[D].济南:山东大学,2010.
Sun Guofu.Theory and Application Study of Sunshine Temperature Effects on Long-Span CFST Arch Bridge[D].Jinan:Shandong University,2010.
[5] 彭友松,强士中,刘悦臣.钢管混凝土圆管拱肋日照温度分布研究[J].桥梁建设,2006 (6):18-24.
Peng Yousong,Qiang Shizhong,Liu Yuechen.Study of sunshine temperature distribution in circular concrete-filled Steel tube arch rib[J] .Bridge Construction,2006 (6):18-24.
[6] 张金.箱-混凝土组合拱桥施工过程力学行为研究[D].重庆:重庆交通大学,2012.
Zhang Jin.Study on the Mechanical Behaviors of Steel Box-Concrete Composite arch Bridge in Construction Stage[D].Chongqing:Chongqing Jiaotong University,2012.
[7] 阮静,万水,叶见曙,等.混凝土箱梁温度场有限元分析 [J].公路,2001 (9):55-58.
Ruan Jing,Wan Shui,Ye Jianshu,et al.Temperature field finite element analysis of concrete box girder [J].Highway,2001(9):55-58.
[8] Elbadry M M,Ghali A.Temperature variations in concrete bridges[J].Journal of Structural Engineering,1983,109(10):2355-2374.
[9] 刘振宇,陈宝春.日照作用下钢管混凝土构件截面温度场有限元分析[J].公路交通科技,2008,25(7):49-53.
Liu Zhenyu,Chen Baochun.Finite element analysis on temperature field of CFST members under solar radiation[J].Journal of Highway and Transportation Research and Development,2008,25 (7):49-53.
[10] BS EN 1993-1-2:2005 Eurocode 3:Design of Steel Structures[S].British:Standards Policy and Strategy Committee,2005.
[11] BS EN 1992-1-2:2004 Eurocode 2:Design of Concrete Structures[S].British:Standards Policy and Strategy Committee,2004.
[12] 朱波,龚清盛,周水兴.连续刚构桥0号块水化热温度场分析[J].重庆交通大学学报:自然科学版,2012,31(5):924-926.
Zhu Bo,Gong Qingsheng,Zhou Shuixing.Analysis of temperature field for block number zero of continuous rigid frame bridge[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31 (5):924-926.

