分幅斜拉桥斜拉索无应力长度的简化计算方法

赵 雷，贾少敏，顾 乡

(西南交通大学 土木工程学院，四川 成都 610031)

0 引 言

斜拉桥通过斜拉索的主动张拉，改善主梁的受力性能[1-2]。若斜拉索加工过长，则会造成斜拉索张拉到位时所需张拉空间加大，且需在拉索锚杯下添加垫片造成结构安全度降低；若斜拉索加工过短，则张拉困难，甚至无法张拉到位[3-4]。准确的斜拉索制造长度是确保拉索顺利张拉到位，进而保证主梁受力合理、成桥线形平顺的关键。通常斜拉索的制造长度是根据成桥线形及成桥索力计算斜拉索的无应力长度，然后考虑锚头构造来确定。确定合理成桥索力是设计的重点也是准确计算无应力索长的前提。对于六塔、分幅、空间四索面的嘉绍大桥而言，由于其结构体系复杂，斜拉索数量庞大，采用直接优化的方法确定其合理成桥索力计算量巨大，笔者基于刚度等效的原理提出了一种索力分步、简化算法；在得到每根斜拉索成桥合理索力后结合斜拉索锚点坐标确定了每根斜拉索的无应力索长[5-8]。

1 工程背景

1.1 工程概况

嘉绍大桥主航道桥为世界上首座六塔独柱四索面分幅钢箱梁斜拉桥，其跨径布置为70+200+ 5×428+200+70=2 680(m)，全桥共576根斜拉索，如图1。由于采用独柱、双幅钢箱梁、四索面结构形式，横桥向4根拉索内、外侧拉索长度及角度均不同，如图2。斜拉索内外侧索面不对称产生不平衡水平分力，使单幅主梁在斜拉索的作用下产生横向变形和弯矩，为抵消主梁横向内力，两幅主梁之间设置了横梁，全桥每隔一个标准梁段设置一道永久横梁。

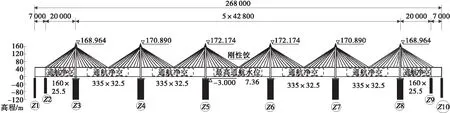
图1 嘉绍大桥桥型布置(单位：cm)

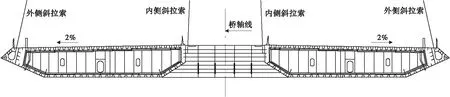
图2 主梁截面Fig.2 Cross section of main girder

1.2 结构计算模型

笔者计算分析时采用西南交通大学桥梁工程系研发的大跨度桥梁非线性分析软件NLABS，该系统可考虑结构的几何非线性行为，具有自动迭代主梁安装线形，按无应力索长施加索力，模拟支架刚度等功能[8-10]。

2 悬链线方程

斜拉桥拉索为斜置悬链线，如图3，将原点设于拉索梁段锚点处，取曲线上任意微元，其在y方向的平衡条件为：

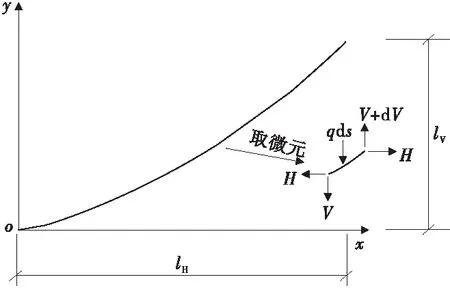
图3 拉索平衡状态Fig.3 Force equilibrium of cable

V+qds=V+dV⟹qds=dV

(1)

式中：V为拉索索力的垂直分量；q为拉索线密度；ds为微元长度。又：

(2)

将式(2)代入式(1)得：

qds=Hy″dx

(3)

此微分方程解为：

(4)

拉索倾角α=arctan(y′)，当x=0时，拉索的力边界条件为：索力T=T0,H=H0，且有：

H0=T0cosα=T0cos[arctan(y′)]

(5)

根据边界条件可得：

(6)

(7)

对式(4)求导后得：

(8)

由拉索的悬链线方程不难得到在索力T作用下，拉索的有应力长度l为：

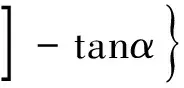
(9)

在索力T作用下拉索的伸长量Δl为：

(10)

无应力长度l0=l-Δl。

当成桥索力确定时，成桥锚点坐标是一定的，因此lV，lH是已知的，q也为已知量，但由于α未知，H0也是未知的，因此两式共有y′和H0两个未知量，可联立求解，显然这是一个非线性方程组，可采用Newton迭代求解。求解出y′和H0后，由拉索平衡条件可知，任意点拉索的水平分力是相同的，因此可由梁端处的y′通过式(6)求解出C1，之后即可由式(9)、式(10)求出无应力索长。

3 合理成桥索力的确定

3.1 等效合理成桥索力

嘉绍大桥为独柱、分幅结构，两幅主梁及对应内外侧拉索关于桥轴线对称(图2)。经计算发现单幅主梁截面抗扭刚度非常大，主桥在横桥向方向上的变形及自身扭转变形十分微小。钢斜拉桥施工时最关心在斜拉索索力及结构自重恒载下主梁的立面线形是否达到设计线形，因此可将空间结构向竖直面内等效。确定合理成桥索力时，为简化计算，基于刚度等效原则，先将空间结构转化为平面结构进行优化计算，如图4。

图4斜拉索编号示意
Fig.4Cablenumber

确定斜拉桥合理成桥状态的方法有多种，如刚性支撑法、最小弯曲能量法、零位移法、倒拆和正装法、无应力状态控制法、影响矩阵法、应力平衡法等[8-10]。零位移法通过索力调整的方式使成桥状态下主梁和斜拉索交点的位移为0，从而使主梁的弯矩达到最小。笔者首先基于零位移法的思想调整索力使主梁结构内力状态达到最优，然后利用切线安装法[8-9]迭代求解主梁安装线形使成桥后主梁线形达到设计线形。

有限元建模时，依据一般斜拉桥的施工工序，建立嘉绍大桥的施工阶段模型，可将主梁、斜拉索、索塔结构的立面投影位置作为模型中主梁、拉索、索塔节点坐标，将原分幅主梁截面刚度等效为一幅主梁截面刚度，横桥向4根拉索合并为1根。嘉绍大桥全桥共576根斜拉索，等效后简化为144根，模型规模、调索数量得到了显著减小。

模型计算时采用切线位置法，即对于Z3～Z8中1～12号标准悬拼梁段，在0号块上吊机安装到位后、悬拼开始前即把1～12号主梁无重单元激活，在对应各标准悬拼梁段精匹配后激活自重荷载；斜拉索单元按既定的施工顺序逐步激活，索力按无应力索长控制。

在等效平面杆系模型中，迭代求解满足成桥线形要求的合理成桥索力，具体操作步骤如下：

1)确定首次计算时拉索初始二张索力。成桥状态下主梁主要受两大力系的作用，一为梁段自重，一为斜拉索张力，这两个力系处于平衡状态。因此可在计算出主梁、横梁自重及二期荷载后，简化结构条件，将恒载合理分配至每根索，粗算平衡恒载的索力(角度可直接采用锚点间夹角)。

2)将1)求得的二张索力代入第2节中介绍的悬链线公式换算无应力索长，拉索锚点坐标可从设计成桥状态中获得。

3)按2)中计算所得无应力索长正装计算得到成桥状态下主梁位移、内力，判断此内力状态是否满足要求。

4)如成桥内力状态未满足要求，则修正二张时无应力索长重新计算。

5)重复3)、4)，即可获得比较好的成桥内力状态和对应的成桥无应力索长及索力。

6)按5)确定的成桥合理索长迭代求解合理安装线形，其流程如图5。

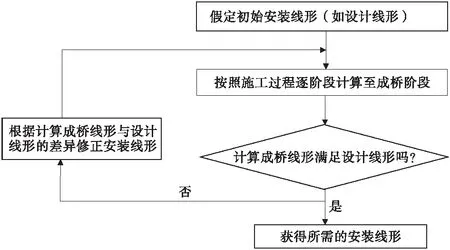
图5 安装线形迭代流程Fig.5 Calculation process of erection profile

至此，求得主桥等效平面结构的合理成桥索力，部分等效平面索力如表1。

表1 等效成桥平面索力Table 1 Equivalent plane cable force upon completion state

3.2 空间成桥合理索力

内外侧索力分配计算基于等效平面成桥索力，按照各梁段锚点所在截面处受力平衡方程推算内外侧索力比例关系。在建立平衡方程时遵循N号斜拉索索力只与N号梁段内所受其它恒载作用保持平衡的原则，即N号斜拉索内外侧索力竖向分力之和=对应N号成桥平面索力的竖向分力/2；N号斜拉索内外侧索力的竖向分力和横桥向水平分力以及N号主梁重及其上所受横梁自重、二期恒载、横梁反力(抵抗斜拉索横桥向水平分力)对截面剪心的力矩之和=0。

由于成桥状态结构处于超静定状态，为便于计算可做如下简化：①计算N号梁段对应内、外侧斜拉索力时，主梁自重取该N号梁段自重(而非前后两个梁段自重之和的一半，各相邻梁重差别不大)；②横梁重按顺桥向位置分配至前后两处竖向支撑处(即斜拉索锚点所在截面)，其对截面剪心作用力矩之力臂取内侧锚点至剪心的横桥向距离；③二期恒载按梁段长度(标准梁段长度15 m)计算合力，合力通过等效作用点对截面剪心作力矩参与到力矩平衡计算；④横梁反力等效作用点取横梁高度的1/2处；此外还需注意边跨12号索及各索塔1号索索力分配计算时，需特别考虑支座反力对扭转的影响。表2列出了Z3索塔对应拉索经等效平面成桥索力转化后，每根索的索力。

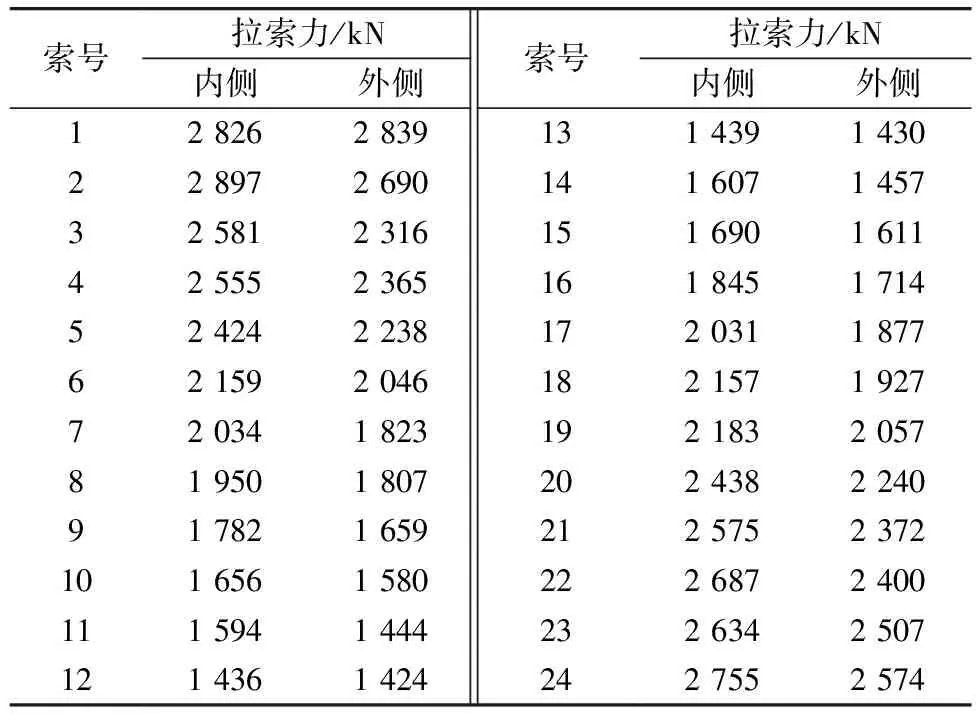
表2 斜拉索成桥真实索力Table 2 Cable force upon completion state

3.3 无应力索长确定

通过3.2节求出主桥空间每根斜拉索的成桥索力后，结合设计图纸中主桥每根斜拉索的空间锚点坐标即可求出斜拉索的无应力索长。表3列出了Z3塔对应斜拉索的无应力索长。

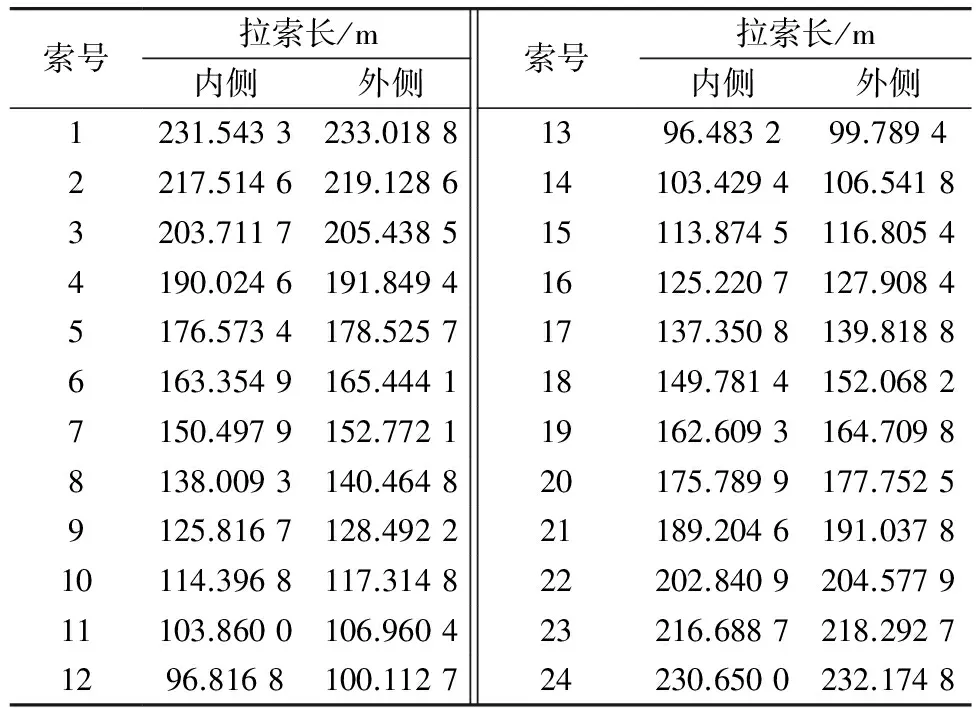
表3 斜拉索无应力长Table 3 Unstessed length of cable

4 结 语

准确的斜拉索无应力长度是确保斜拉索制造长度合适进而保证结构成桥受力合理的关键；合理的成桥索力是精确计算斜拉索无应力长度的前提。多塔、分幅斜拉桥结构体系复杂，斜拉索数量较多，直接对其进行优化时设计变量繁多，计算复杂。笔者基于刚度等效的原则，将空间结构简化为平面结构，在此基础上基于“零位移”的思想对平面索力进行优化，然后将其通过合适的索力分配关系转化为空间索力进而最终确定空间每根斜拉索的无应力长度。嘉绍大桥实际施工时，未发生斜拉索过长需加垫片或过短张拉困难的现象，该方法计算思路明确，计算效率高，可为今后同类斜拉桥斜拉索制造长度确定提供借鉴。

[1] 项海帆.高等桥梁结构理论[M].北京:人民交通大学出版社,2001.

Xiang Haifan.Advanced Theory of Bridge Structure[M].Beijing: China Communications Press, 2001.

[2] 刘士林.斜拉桥[M].北京:人民交通出版社,2002.

Liu Shilin.Cable-Stayed Bridges[M].Beijing: China Communications Press, 2003.

[3] 方志,李学有.斜拉索无应力长度求解及成品索长合理确定[J].桥梁建设,2009(4): 54-58.

Fang Zhi, Li Xueyou.Calculation of unstressed length and reasonable determination of finished length of stay cable[J].Bridge Construction, 2009(4): 54-58.

[4] 潘涛,田仲初.九江湖口大桥斜拉索成品索长计算方法[J].国外公路,2000, 20(5): 46-48.

Pan Tao, Tian Zhongchu.Algorithm for calculating finished length of stay cable in Jiujiang Hukou bridge[J].Journal of Foreign Highway, 2000, 20(5): 46-48.

[5] 聂建国,陈必磊,肖建春.已知索端预张力或预应力状态索长的索原长求解技术[J].工程力学,2003, 20(6): 81-85.

Nie Jianguo, Chen Bilei, Xiao Jianchun.Analysis of the un-stressed length of catenary with known stressed length or end tension force[J].Engineering Mechanics, 2003, 20(6): 81-85.

[6] 郝超,裴岷山,强士中.大跨度斜拉桥斜拉索无应力长度的计算方法比较[J].重庆交通学院学报,2001, 20(3): 1-3.

Hao Chao, Pei Minshan, Qiang Shizhong.Comparison of algorithm for calculating non-stress length of cables in long-span cable-stayed bridge[J].Journal of Chongqing Jiaotong University, 2001, 20(3): 1-3.

[7] 秦顺全.无应力状态法——斜拉桥安装计算的应用[J].桥梁建设,2008(2): 13-16.

Qin Shunquan.Application of unstressed state control method to calculation for erection of cable-stayed bridge[J].Bridge Construction, 2008(2): 13-16.

[8] 李乔,卜一之,张清华.大跨度斜拉桥施工全过程几控制概论与应用[M].成都:西南交通大学出版社,2009.

Li Qiao, Bu Yizhi, Zhang Qinghua.Conspectus of the Geometry

Control Method of the Whole-Procedure of Long-Span Cable-Stayed Bridge and Application[M].Chengdu: Southwest Jiaotong University Press, 2009.

[9] 杨兴旺.大跨度斜拉桥施工全过程非线性行为研究[D].成都:西南交通大学,2007.

Yang Xingwang.Research on the Nonlinear Behavior of Long-Span Cable-stayed Bridges Considering overall Construction Process[D].Chengdu: Southwest Jiaotong University, 2007.

[10] 孟繁增.多塔斜拉桥合龙方法及其影响研究分析[D].成都:西南交通大学,2012.

Meng Fanzheng.Study on Closrue Scheme and Its Influence on Structural Stage for Multi-Pylon Cable-Stayed Bridges[D].Chengdu: Southwest Jiaotong University, 2012.