基于类中心的SVM训练样本集缩减改进策略

庞首颜,陈 松,魏建猛,张元胜

(1. 重庆交通大学 信息科学与工程学院，重庆 400074；2.重庆第二师范学院，重庆 400065)

0 引 言

SVM(支持向量机)以其优越的性能，在许多领域中得以实际应用。但由于训练样本集规模较大引发的学习速度慢、存储需求量大、泛化能力降低等问题 ,成为直接使用该技术的瓶颈。究其原因，SVM在模式识别方面的应用过程，归根结底为一个线性的凸二次规划优化问题的求解过程(QP)[1]。对于n个训练数据,n×n维核函数矩阵的计算和矩阵与向量相乘计算导致求解过程需要大量的时间开销, 所以样本数量越大，求解速度则越慢。如何提高训练速度和减少内存开销则成为研究 SVM 的一个新问题。

总结近年来研究人员在该优化问题上使用的研究方法，主要有以下两个方面：

1)在不改变训练集大小的前提下，把问题分解成为一系列易处理的子问题来解决，从而提高训练的速度。并按其迭代策略的不同分为Chunking算法[2]、Osuna 算法[3]、SMO 算法[4-5]等。其不足的地方是：这些算法需要通过反复迭代来寻找最优解，当训练样本数量较大时，收敛速度可能会比较慢。

2)通过去除训练集中与支持向量无关的样本来提高支持向量机的学习效率。基本思想是:从训练集中删减对学习没有帮助甚至有反作用的样本,缩减训练样本集,同时保证分类器的分类正确率不降低甚至有所提高, 从而减少训练的代价，提高训练速率。如焦李成，等[6]提出了支撑矢量预选取的中心距离比值法；汪西莉，等[7]提出了基于马氏距离的支持向量快速提取算法；李青，等[8]提出了基于向量投影的支撑向量预选取方法；李红莲，等[9]提出了NN_SVM；郭亚琴，等[10]提出了BS_SVM；朱方，等[11]通过点集理论提出一种大规模训练样本集缩减策略等。

笔者提出了一种改进的缩减训练集的方法。首先根据各样本点到样本集中心的矢量距离，构造超球；然后通过只提取超平面及距离超平面较近的样本实现边界样本的提取，从而实现样本集的缩减。

1 支持向量机

支持向量机可用于模式识别、回归分析、主成分分析等。下面以模式分类为例来介绍支持向量机的含义。

定义1 (最优分类超平面)如果训练样本可以被无误差地划分，以及每一类数据中离超平面最近的向量与超平面之间的距离最大，则称这个超平面为最优分类超平面。

1.1 线性支持向量机

在求解两类线性可分的问题时, SVM实质就是通过在输入空间求得一个分类超平面w·x+b=0, 使两类样本到该超平面之间的距离为最大(即找到其最优超平面)，从而实现两类样本的最优划分。

设训练样本为(x1,y1),(x2,y2),…,(xl,yl),xi∈Rn为描述样本的n维特征向量，yi∈{+1,-1}代表xi所属的类别。因为可能存在有样本不能被超平面正确分类, 所以引入松弛变量ξ，结合正则超平面min|ω·x+b|=1，求最优超平面的问题则可归结为以下优化问题:

s.t.yi((xi·ω)+b)≥1-ξi，ξi≥0，

i=1,…,k。

(1)

此时,支持向量机可以看作是寻找一个分类超平面,该超平面通过设定一个惩罚因子C, 在最大间隔和最小错分误差两者之间取一个折中；引入Lagrange 乘子α,β,将上述问题转化为对偶形式。

(2)

根据Karush-Kuhn-Tucker定理，在鞍点有：

(3)

简化后有：

αi[yi(xi·ω)+b-1]=0

(4)

由式(4)可知,对于大多数的样本来说，其αi的值将为0；而αi取值不为0所对应的样本即为该优化问题的支持向量sv,它们的数量通常只占全体样本数量较少的比例。

最后根据支持向量和简化式可求出b，则决策函数为(sv为支持向量)：

(5)

因此，在确定的空间中，可以得到定理1，它是SVM进行样本集缩减的主要理论依据[11]。

定理1 支持向量机的训练结果与非支持向量无关。

1.2 非线性支持向量机

在求解非线性分类问题时，SVM首先使用一个非线性映射Φ将输入映射到线性可分的高维特征空间，然后通过在特征空间中求最优超平面来实现问题的求解。因为在进行决策函数和优化问题计算时都只需要进行特征空间中的内积运算，由Mercer定理可知，可以通过选取一个满足条件的核函数K(x,xi)，来替代特征空间中的内积运算Φ(x)·Φ(xi)，从而避免了显式定义映射Φ的定义。即K(x,xi)=Φ(x)·Φ(xi)，则此时的优化问题为：

(6)

则决策函数为：

(7)

通过引进核函数，SVM巧妙地解决了在将低维空间向量映射到高维空间向量时带来的“维数灾难”问题。

2 基于类中心的样本集缩减策略

2.1 支持向量机几何基础知识

从文献[12]的命题可知，假如映射到特征空间后的两类样本集是可分的，则最优分类超平面位于两类样本集的类中心之间(图1)，并且各类的支持向量(即图中的带圈部分)分布于类别中心和最优超平面之间。从几何上直观地看，支持向量就是在线性可分的空间中两类样本的交遇区内那些离最优超平面最近的两类边界上的样本[8]。

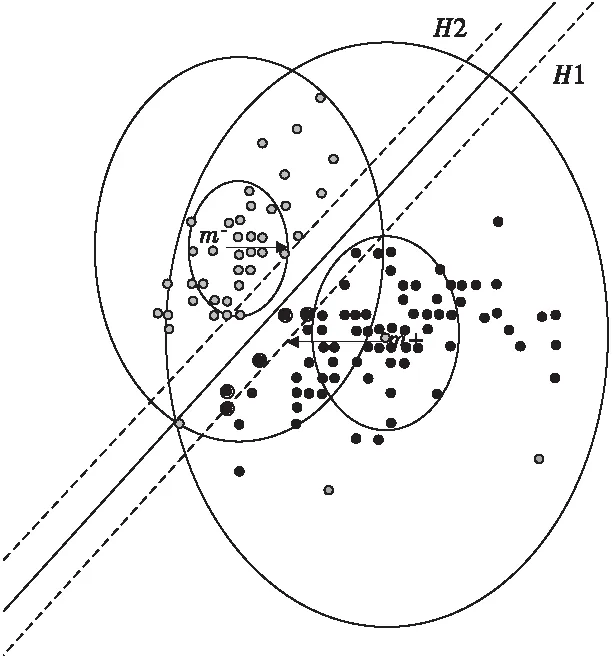
图1 最优超平面与类中心的关系Fig.1 Relationship between optimal hyperplane and class-center

笔者的研究主要根据支持向量本身的结构特点，剔除对超平面构造没有实际意义的样本点，保留处于边界位置的样本(这部分样本最有可能成为支持向量)来参与超平面的构建，进而降低计算量并提高超平面构建速度。具体设计思路如下：

1)如图2，L1，L2分别为过正类、负类中心且平行于超平面H的一条直线，S+，S1+分别为过正类中心m+的一个圆，S-，S1-分别为过负类中心m-的一个圆，S′+，S′-分别为S+，S-彼此靠近的两个半圆。首先利用文献[13]中的基于类中心的边缘方法找到位于L1，L2之间的样本点，即S1′+，S1′-内的点。

2)在1)基础上通过样本点到样本中心点的距离来缩减支持向量的预选范围，从而获得边界样本信息。

3)以2)中得到的边界样本为训练样本完成SVM训练。

4)利用3)训练得到的SVM对样本点进行分类。

图2 最优超平面与样本点结构的关系Fig.2 Relationship between optimal hyperplane and data structure

2.2 线性可分的支持向量预选取

2.2.1 文中用到的定义

定义1 某一类样本的平均特征称为该类样本的中心m，已知样本向量组{x1,x2,…,xl}，其中l为其样本个数，那么其中心为:

(8)

定义2 样本距离是指两个样本之间的特征差异，已知两个N维样本向量x1,x2，则其样本距离为:

(9)

2.2.2 基于类中心边界向量预取算法

1)将原始训练样本根据标号的不同分成两类S+,S-。l+为正类样本的个数,l-为负类样本的个数, 其中l=l++l-。

2)分别计算正类样本的类中心m+、负类样本的类中心m-，各个样本点到各自样本中心点的距离d(xi,m±)；

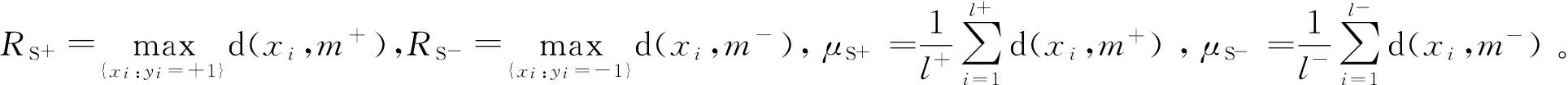
4)由文献[13]的去边缘方法使得与支持向量相关的两个半球内的样本点：

S′+={x|(m--m+)·(x-m+)≥0,x∈s+}

S′-={x|(m+-m-)·(x-m-)≥0,x∈s-}

(10)

5)通过公式：

(11)

来确定正类、负类样本集中各自所对应的边界样本。其中0 <λ1±,λ2±< 1，其具体的取值取决于样本的分布情况。考虑样本点分布的结构特点，文中λ1与各自均值距离与其半径的比值相关。同时，为了进一步减少孤立样本点对训练结果的不良影响，引人了λ2，其取值与处于样本边缘且个数小于样本总个数1/100的样本相关。

2.3 非线性可分的支持向量预选取

由非线性支持向量机可知，在进行非线性可分的问题求解时,首先通过某个非线性映射Φ将训练样本从输入空间映射到某一高维(甚至无穷维)的特征空间H，使其在特征空间中呈现线性(或近似线性)可分，然后再在特征空间中构造最优分类超平面。则映射到特征空间后任意两点间的距离可由以下引理1求出。

引理1[4]已知两个向量x=(x1,x2,…,xn)和y=(y1,y2,…,yn)，经过非线性映射Φ(x)作用映射到特征空间H中，则这两个向量在特征空间中的Euclidean 距离为：

(12)

其中K(·,·)是以上提到的核函数。在这里需要注意的是：在输入空间中的样本类中心经映射后得到的值不再是特征空间中的样本的中心矢量。设n是样本的个数，则特征空间样本的中心矢量mΦ须在特征空间中求得：

(13)

但是因为映射Φ(x)没有进行显式的定义，所以无法直接根据式(13)来得到特征空间中样本集的中心矢量。至今也仍没有一个统一的计算公式来进行直接的计算，为此，焦李成，等[6]给出了一个引理来计算该样本的中心矢量，但计算复杂，且运算量较大。为了避免该难题，目前更多的方法是通过聚类方法来得到特征空间的类中心，如模糊SVM，超球SVM等都是通过聚类的方法来确定类中心等。罗瑜[12]则是根据统计学的观点和样本信号的离散型，在训练集样本是i.i.d.的条件下，从训练集中随机抽取部分样本代替整体样本来计算类别质心。为了简化运算及提高运算的速度，本人利用近似替代的方法来获取样本中心，也就是通过在特征空间中寻找能生成最小超球的样本点来代替特征样本的中心矢量。其具体的算法如下：

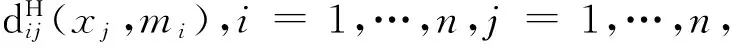
2)则该样本集的超球的半径为：Rs=min(Ri),i=1,…,n。而该Ri所对应的圆心样本点便可作为该样本集在特征空间中的中心矢量。

3 实验结果

3.1 实验环境

实验采用台湾林智仁LIBSVM官方学习网站http://www.csie.ntu.edu.tw/～cjlin/数据库里的breast-cancer，heart-statlog，a7a，german.-number，iris数据集，其具体信息见表1。

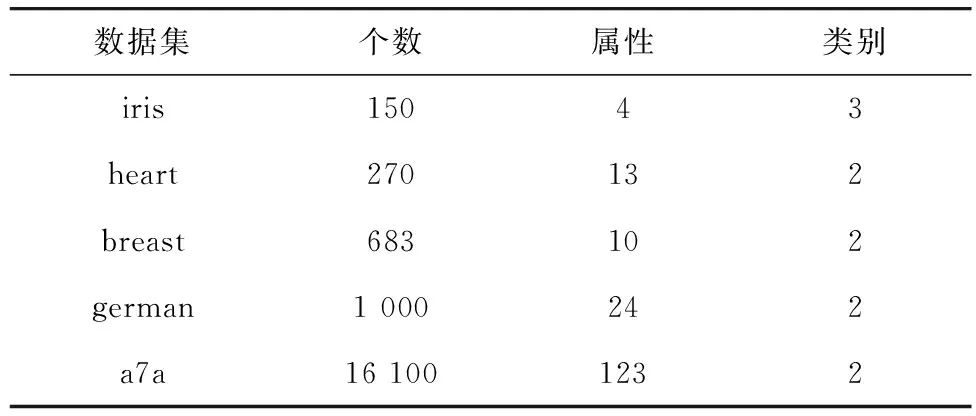
表1 实验数据集

表中iris的类别为3类，实验中，以1类为+1类，2类和3类一起作为-1类进行实验。此外训练样本数目与测试样本数目的比例中，除heart数据集的比例为170 ∶100，和另外的german数据集的比例为750 ∶250以外，其他样本集均按8 ∶2的比例进行实验。且所有实验都是在PC机(奔腾2.0 GHz，2.0 G内存)，MATLAB R2011b，LIBSVM-3.12环境下进行的。

3.2 与SVM比较

表2中列出了各种数据集在文中方法和SVM方法下的样本数目，训练样本数目，训练时间，训练准确率及预测准确率等。其结果均为10次实验后取的平均值。

表2 文中方法与SVM的比较

从表2的结果可以发现，就训练准确率和预测准确率而言，通过文中方法，iris数据集的训练准确率和预测准确率均为100%；heart、breast数据集的训练准确率和预测准确率均提高了1%左右； german、a7a数据集则在和准确率上降低了0.5%～5.0%之间。可见，文中方法更适用于样本数目中等的训练样本集。此外，就训练样本数目和训练时间而言，通过本文方法大大缩减了训练样本集且较大的提高了训练时间，这个特点在大样本数据集上表现较为明显。

4 结 语

采用改进的基于类中心的支持向量机训练样本缩减策略，筛选出超平面附近的边界样本来训练分类器，在样本集数目适中的情况下，其训练准确率和预测准确率稍优于标准支持向量机，而且训练速度则提高了许多。但仍存有不足，改进的算法需要消耗时间进行边界样本寻找，无形地增加了时间开销。此外，笔者还就非线性可分时，无法直接计算特征空间中的类中心问题，提出了利用近似替代方法。通过在特征空间中寻找能生成最小超球的样本点来代替特征样本的中心矢量，实验证明，该方法是现实可行的。

[1] 奉国和,李拥军,朱思铭.边界临近支持向量机[J].计算机应用研究,2006(4):11-12.

Feng Guohe,Li Yongjun,Zhu Siming.Boundary nearest support vector machines [J].Application Research of Computers,2006(4):11-12.

[2] Cortes C,Vapnik V.Support-vector networks [J].Machine Learning,1995,20(3):273-297.

[3] Osuna E,Freund R,Girosi F.An improved training algorithm for support vector machines[C]// Principe J,Gile L,Morgan N,et al.Neural Networks for Signal Processing Ⅶ.Amelia Island,F L:Proceedings of the 1997 IEEE Workshop,1997:276-285.

[4] Platt J C.Fast training of support vector machines using sequentia1 minima1 optimization[C]//Schölkopf B,Burges C J C,Smola A J.Advances in Kernel Methods-Support Vector Learning.Cambridge:MIT Press,1998:185-208.

[5] Platt J C.Using analytic QP and sparseness to speed training of support vector machines [C]//Kearns M S,Solla S A,Cohn D A.Advances in Neural Information Processing Systems.Cambridge: MIT Press,1999:557-563.

[6] 焦李成,张莉,周伟达.支撑矢量预选取的中心距离比值法[J].电子学报,2001,29(3):383-386.

Jiao Licheng,Zhang Li,Zhou Weida.Pre-extracting support vectors for support vector machine [J].Chinese Journal of Electronics,2001,29 (3):383-386.

[7] 汪西莉,焦李成.一种基于马氏距离的支持向量快速提取算法[J].西安电子科技大学学报:自然科学版,2004,31(4):639-643.

Wang Xili,Jiao Licheng.A fast algorithm for extracting the support vector on the mahalanobis distance [J].Journal of Xidian University:Natural Science,2004,31(4):639-643.

[8] 李青,焦李成,周伟达.基于向量投影的支撑向量预选取[J].计算机学报,2005,28(2):145-152.

Li Qing,Jiao Licheng,Zhou Weida.Pre-extracting support vector for support vector machine based on vector projection [J].Chinese Journal of Computers,2005,28(2):145-152.

[9] 李红莲,王春花,袁保宗.一种改进的支持向量机NN_SVM [J] .计算机学报,2003,26(8):1015-1020.

Li Honglian,Wang Chunhua,Yuan Baozong.An improved SVM:NN_SVM [J].Chinese Journal of Computers,2003,26(8):1015-1020.

[10] 郭亚琴,王正群.一种改进的支持向量机BS_SVM[J].微电子学与计算机,2010,27(6):54-56.

Guo Yaqin,Wang Zhengqun.An improved SVM:BS_SVM [J]. Microelectronics & Computer,2010,27(6):54-56.

[11] 朱方,顾军华,杨欣伟,等.一种新的支持向量机大规模训练样本集缩减策略[J] .计算机应用,2009,29(10) :2736-2740.

Zhu Fang,Gu Junhua,Yang Xinwei,et al.New reduction strategy of large-scale training sample set for SVM [J].Journal of Computer Applications,2009,29(10):2736-2740.

[12] 罗瑜.支持向量机在机器学习中的应用研究[D].成都:西南交通大学,2007.

Luo Yu.Study on Application of Machine Learning Based on Support Vector Machine [D].Chengdu:Southwest Jiaotong University,2007.

[13] 曹淑娟,刘小茂,张钧,等.基于类中心思想的去边缘模糊支持向量机[J].计算机工程与应用,2006,42(22):146-149.

Cao Shujuan,Liu Xiaomao,Zhang Jun,et al.Fuzzy support vector machine of dismissing margin based on the method of class-center [J].Computer Engineering and Applications,2006,42(22):146-149.