无人飞行器背景磁场学习方法研究

周建军，林春生，赵建扬

(海军工程大学 兵器工程系，湖北 武汉430033)

0 引言

航空磁测技术被广泛应用于地质调查、矿产勘探、组合导航和地球物理研究等领域，是航空地球物理的一种主要方法［1-3］。在飞行器背景下，补偿飞行器背景磁干扰是航磁测量的一项关键技术。飞行器搭载磁传感器测量时，飞行器的固有磁场以及飞行器机动时产生的磁干扰会对测量值产生较大的干扰。20 世纪40年代，文献［4 -5］建立了飞行器的磁场模型。之后Bickel［6］提出了一种基于小幅度机动的模型求解方法，其提出的小信号模型要求飞行器在补偿飞行器背景磁场前进行四航向的机动学习飞行。但文献［6］中并没给出详细的推导过程。学习飞行的航线示意图如图1所示［7］。此外，有报道指出，俄罗斯在学习飞行时选取的是一种圆周飞行的学习航线。

当利用一些无人飞行器进行航磁测量时，由于机动受限，要求飞行器做一个封闭的四航向学习飞行是非常困难的，为了解决无人飞行器在模型求解前的学习飞行问题，本文将封闭四航向的学习路径改为折线飞行的学习路径，对不同折线路径的学习效果进行了比较分析，同时分析了航向数对学习效果的影响。

1 飞行器背景磁场建模

飞行器背景磁场主要包括飞行器的剩余磁场、感应磁场和涡流磁场3 部分。以飞行器上磁传感器为坐标原点，建立坐标系如图2所示，其中x 轴与飞行器纵轴平行，向前为正;y 轴与飞行器横轴平行，向右为正;z 轴与飞行器的垂直轴平行，向下为正。Bd表示飞行器背景磁场矢量，Bo为地磁场矢量，Bc为磁传感器测量的地磁场与飞行器背景磁场的合成磁场，即

α、β、γ 为x、y、z 轴与Bo的夹角。设u1=cos α，u2=cos β，u3=cos γ. 根据Tolles 和Lawson 提出的飞行器磁场模型，飞行器背景磁场［6］可以表示为

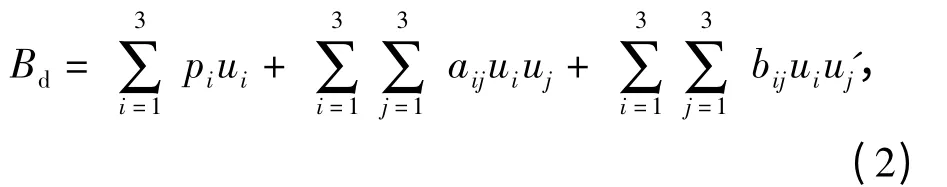
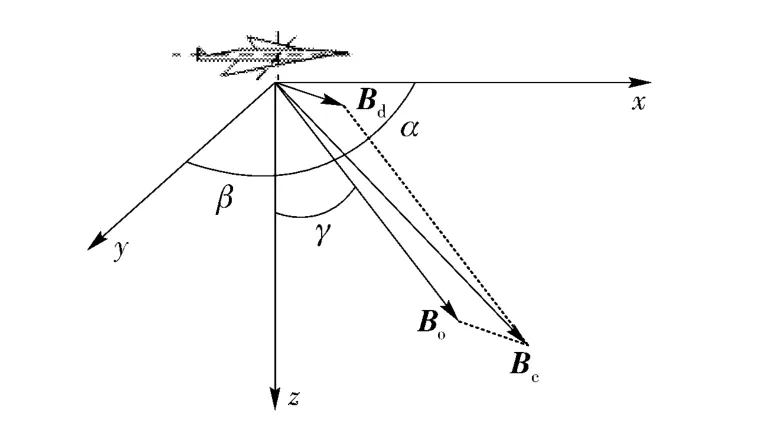
图2 飞行器磁场模型坐标系Fig.2 Coordinate system of aircraft magnetic field model

式中:pi、aij和bij分别为飞行器的剩磁参数、感磁参数和涡磁参数;u'j为方向余弦uj的导数。且aij=aji，a33=0，b33=0. 那么总的模型系数一共有16 项。

2 飞行器背景磁场模型求解

Tolles-Lawson 模型将飞行器背景磁场的物理模型转化为了数学模型，但模型阶数较高，方程存在较强的复共线性。为了精确求解出飞行器的背景磁场参数，美国学者Bickel 提出了“小信号模型”的概念，下面给出该模型的推导过程。

当飞行器沿直线作小幅度机动，该直航向下地磁场Hd与x、y、z 轴的夹角为θi0，机动引起的角度变化量为Δθi(t)，那么近似有

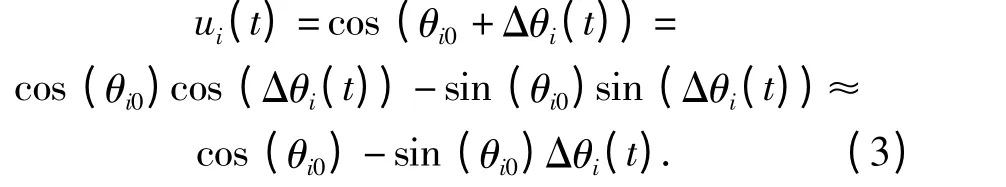
因而ui(t)可以表示为

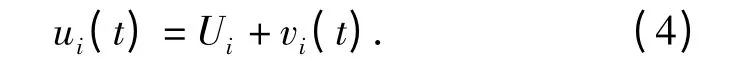
式中:Ui=cos(θi0)，Ui是与直航向有关的方向余弦稳定量;vi(t)= -sin (θi0)Δθi(t)，vi是在对应直航向上与飞行器机动有关的方向余弦变化量。当机动角度Δθi(t)≤6°，(4)式的误差≤0.5%.

将(4)式代入(2)式，并忽略vi的二阶小项可以推导出由于飞行器机动引起的背景磁场变化量为

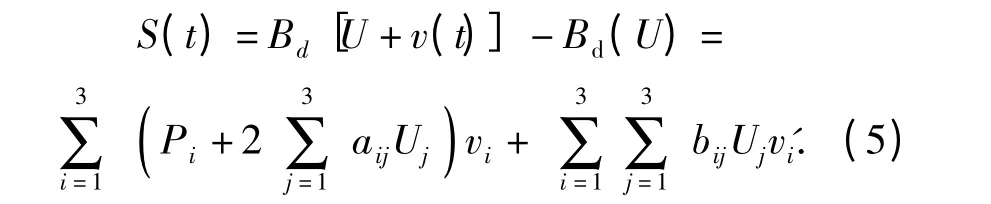
下面以中高纬度地区为例给出小信号模型的求解方法，在中高纬度地区，当磁纬度大于30°，图2中r ＜60°，因而U3≥0.5. 由于

将(4)式代入(6)式并忽略vi的二阶小项可以推导得到

对(7)式求导可以得到

由(7)式与(8)式可以得到

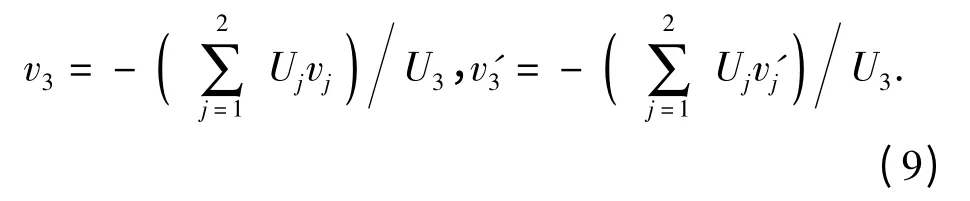
将(9)式代入(5)式，飞行器机动引起的背景磁场变化量可以改写为

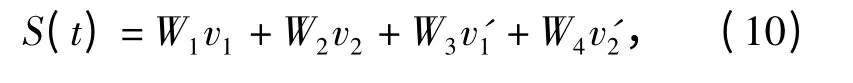
式中:

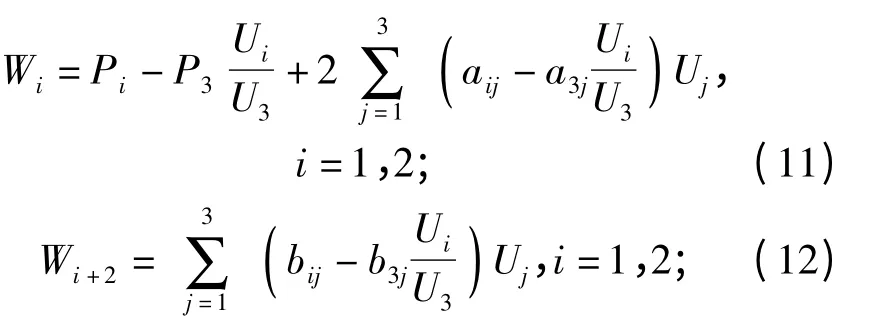
Wi是与航向有关的参数，称为航向参数，记不同航向下的航向参数为Wik，k 表示航向号;S(t)、vi是通过传感器测量后滤波输出的已知量。在k 航向下求解(10)式就可以求出航向参数Wik.

(11)式只与飞行器的剩磁参数与感磁参数有关，将(11)式改写为矩阵形式可以得到如下形式的方程组

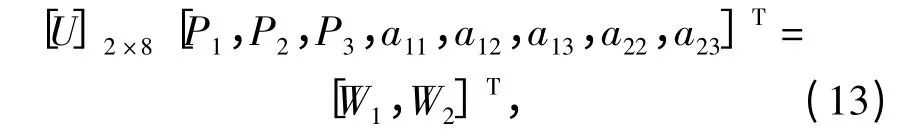
式中［U］2×8是与直航向上方向余弦有关的系数矩阵，表达式可由(11)式推导，其值可以通过传感器测量得到。(13)式共有8 个未知量，因而至少采集4 个航向的飞行数据，由(13)式即可以求出飞行器的剩磁参数与感磁参数。

(12)式只与飞行器的涡磁参数有关，同理可知至少采集4 个航向的飞行数据，即可求出飞行器的涡磁参数。

当飞行器做大范围机动时，地磁场的空间梯度将对飞行器机动产生的背景磁场产生影响。地磁场主要在北向分量与垂直分量上具有较大的量值，因而主要考虑地磁场北向梯度kx与高度梯度kh的影响。在实际工程应用中，可以通过飞行器沿南北航向飞行的磁场数据以及同航向上不同高度的磁场数据估算出kx与kh的均值，得到kx与kh后，在求解航向参数方程(10)式之前，只需要预先对空间磁场梯度进行补偿，即

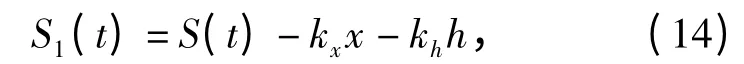
式中:x 与h 分别为飞行器机动引起的北向位移与高度的变化量。然后由(15)式求出航向参数Wi，

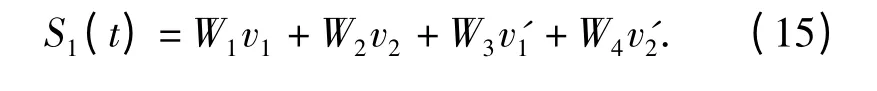
3 飞行器学习路径讨论

在地磁测绘应用中，飞机学习时是绕着一个封闭的四航向区域进行飞行。针对一些机动性能较差的无人飞行器，要求飞行器做一个封闭的四航向学习飞行是非常困难的。为了同样达到学习飞行的目的，探讨将封闭的四航向学习路径改为折线飞行的学习路径，同时考虑航向数大于4 的情形。为了讨论问题的方便，规定飞行器不能反向飞行，飞行器变换航向时一次性转向角度假定飞行器改变航向时每次的转向角度相同，改变一次航向后，需要在新航向上持续飞行一段时间。考虑到地磁场在北向上具有较大的量值，规定飞行器在学习飞行时，折线飞行的朝向为东西方向。这里设定飞行器的初始航向为90°，即朝东飞行，学习飞行后飞行器回到原来的初始航向上。定义飞行器从初始航向到恢复初始航向的飞行阶段为学习飞行阶段。

学习飞行的路径示意图如图3所示。

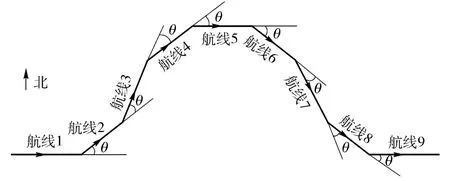
图3 飞行器折线飞行学习路径Fig.3 Fold flight path of aircraft

由示意图可知，飞行器从初始航向进入学习飞行阶段到恢复初始航向过程中的各条航线存在重复的航向，理论上重复的航向对于求解模型参数是冗余的，因而对于重复的航向只需要选取其中的一条作为学习的航向即可。折线学习飞行时的最大航线数是与转向角度θ 相关的，规定飞行器左转时，θ 为正，下面对不同转向角度θ 下的航线规划进行讨论。

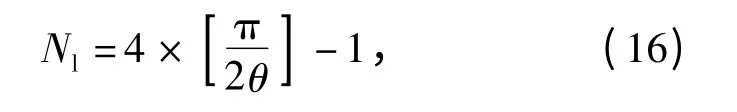
而独立的航向数满足

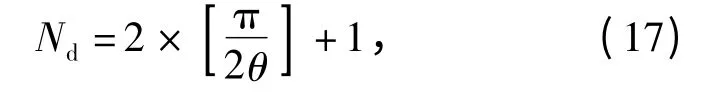
式中［］表示向下取整。

4 飞行器背景磁场参数的求解

在第2 节中推导得知，要求解飞行器的背景磁场参数，飞行器在学习飞行时至少要在4 个航向上做机动飞行，下面针对第3 节所规划的飞行器学习路径对背景磁场参数进行求解，通过检验求解的结果来验证能否通过本文所提出的折线飞行路径进行飞行器背景磁场参数的学习求解。

这里利用开发的飞行器背景磁场仿真软件模拟飞行器的实际飞行过程，仿真软件界面如图4所示。

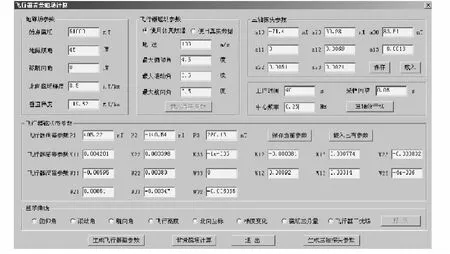
图4 飞行器背景磁场仿真软件界面Fig.4 Simulation software of aircraft’s background magnetic field

软件包括3 个主要模块:

1)参数设置模块。如图4所示，飞行器磁状态参数表示了飞行器的磁状态，对于特定的飞行器来说，其磁状态参数在短期内保持不变，因而通过设定磁状态参数即可选定飞行器。通过飞行器运动参数可以设定飞行器的飞行速度，以及机动时的角度幅值。通过地磁场参数可以设定飞行器飞行区域的磁场值、磁纬度、磁梯度，以及飞行器飞行的磁航向。通过设定三轴探头参数模拟实际的非正交三轴探头输出。界面中，工作时间表示机动飞行的时间，采样间隔表示传感器的采样率，中心频率表示飞行器机动时的中心频率。

2)飞行器背景磁场计算与数据保存模块。根据当前设置的参数，点击“背景磁场计算”按钮后，模拟生成飞行器在设定区域机动飞行时的背景磁场矢量。模拟产生的量还包括飞行器的机动角度、飞行高度、北向坐标、地磁场的方向余弦。

3)显示模块。可以根据选择显示计算后的数据曲线。

这样通过改变相关参数，利用开发的飞行器背景磁场软件就可以模拟飞行器在不同航向下机动飞行产生的磁场矢量值。下面在不同飞行路径条件下对飞行器的背景磁场参数进行求解。

第1 步:设定飞行参数。首先选定飞行器，即设定飞行器磁状态参数真值如表1所示。同时设定飞行器的速度v =100 m/s，机动时的俯仰角、滚动角、航向角幅值为4.5°，飞行器机动时的中心频率为0.25 Hz，每次机动动作的时间为40 s，磁传感器的采样频率均为20 Hz，不考虑三轴磁传感器的非正交因素，学习区域的地磁倾角为45°，即飞行器在中高纬度飞行，学习区域的北向磁场梯度为kx=8.5 nT/km，高度梯度为kh= -19.52 nT/km. 飞行器进入学习航向前的始点地磁场为51 000 nT.

表1 不同飞行路径下计算的模型参数Tab.1 The calculated parameters in different flight path

第2 步:产生飞行器在不同航向下机动飞行时的背景磁场数据样本。这里一共产生3 组数据样本，第1 组数据按照图1所示的0°、90°、180°、270°的封闭航向产生。第2 组数据按照图3所示，当转向角θ 为45°时的航向产生，那么共有0°、45°、90°、135°、180° 5 条航向。第3 组数据按照图3所示，当转向角θ 为30°时的航向产生，那么共有0°、30°、60°、90°、120°、150°、180° 7 条航向。产生的仿真数据样本如图5所示，图示为预先对地磁梯度进行补偿后的磁场数据，其中Bx、By、Bz分别表示在飞行器上三轴磁通门测量值，B 表示光泵测量的磁场值。

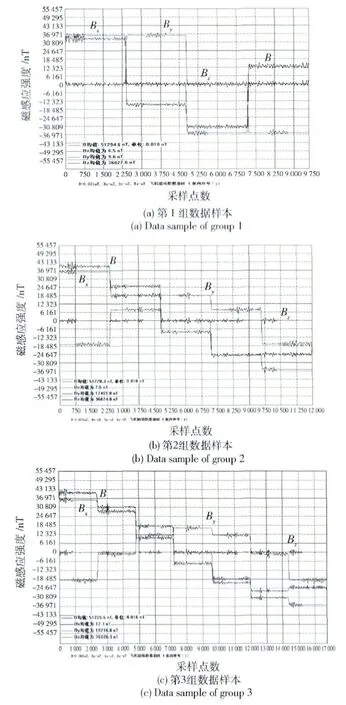
图5 飞行器背景磁场数据样本Fig.5 Data samples of aircraft＇s background magnetic field

第3 步:利用产生的飞行器机动学习数据样本进行模型参数的求解。

表1分别列出了设定的模型参数真值与利用3 组数据样本进行求解的计算值。在计算模型参数时，将所有航向的数据都用于模型求解中。

由表1可以分别得到计算的剩磁参数、感磁参数、涡磁参数与真值的均方根误差RMSE，如表2所示。

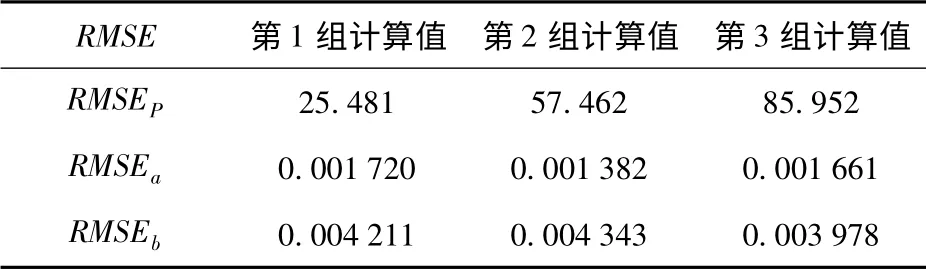
表2 模型参数的均方根误差Tab.2 RMSE of calculated parameters

由计算的结果来看，3 组计算值均能够趋向于模型参数的真值，比较每组计算参数与真值的均方根误差可知，第1 组的剩磁参数更接近真值，而第2组的感磁参数更接近真值，第3 组的涡磁参数更接近真值。为了更为直观地检验所计算的模型参数能否达到补偿飞行器背景磁场的目的，利用3 组计算的模型参数补偿同一条飞行路径下的背景磁场，该条飞行路径按照同样的方法仿真产生:飞行器磁航向为15°，飞行时同时做俯仰、横滚、摇摆机动，机动幅度均为1.5°. 图6给出了补偿结果。

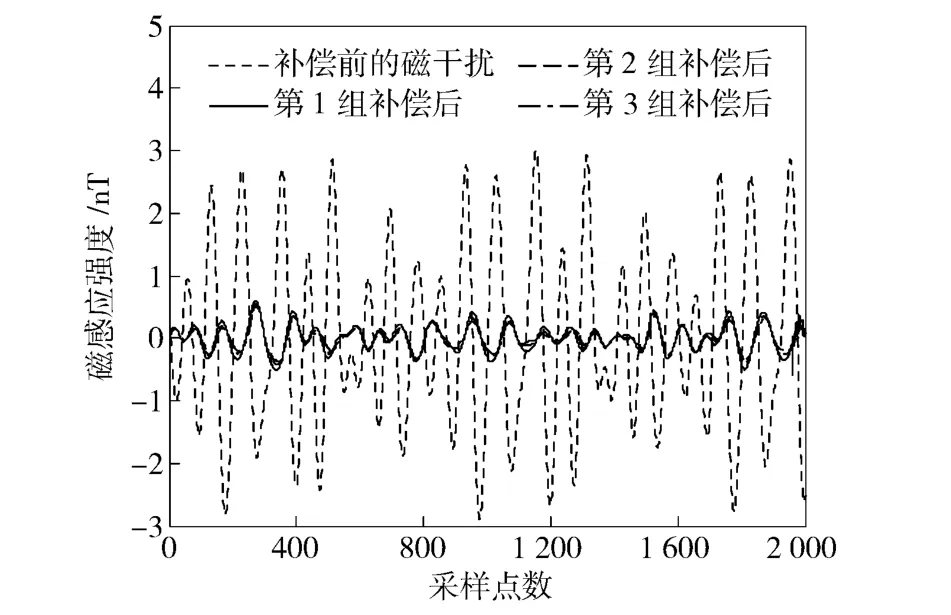
图6 补偿后的飞行器磁干扰Fig.6 The aircraft’s magnetic field after compensation

从补偿结果来看，3 组模型参数的补偿效果相近。因而证明了飞行器按照折线路径进行学习飞行可以达到求解飞行器背景磁场参数的目的。事实上，为了模拟在飞行器舱内进行测量的情形，设定参数真值时，有意增大了飞行器的剩余磁场，x 轴方向上的剩余磁场达到405 nT. 在实际测量中，当飞行器的剩余磁场过大，补偿的效果将会受到影响，这主要是由于剩余磁场叠加在磁通门传感器测量值中，影响方向余弦的计算精度，同时也会增大光泵所测得的因飞行器机动引起的小量值。目前，利用Tolles-Lawson 模型进行补偿的精度可以达到90% 以上［8］。如果飞行器剩余磁场过大，补偿后的背景磁场仍会达到较大的量值，因而必须通过一些磁环境净化方法减小飞行器的剩余磁场，或者对磁通门测量值进行校正。

下面讨论折线飞行时，学习的航向数对求解模型参数的影响，选取图3所示，当转向角θ 为30°时的折线路径。分别选取航向0°、30°、60°、90°;航向0°、30°、60°、90°、120°，航向0°、30°、60°、90°、120°、150°作为学习数据的样本。结合表1的第3 组学习数据，就可以讨论当增加航向数时能否达到改进模型参数的目的。表3给出了不同航向数下求解的模型参数。

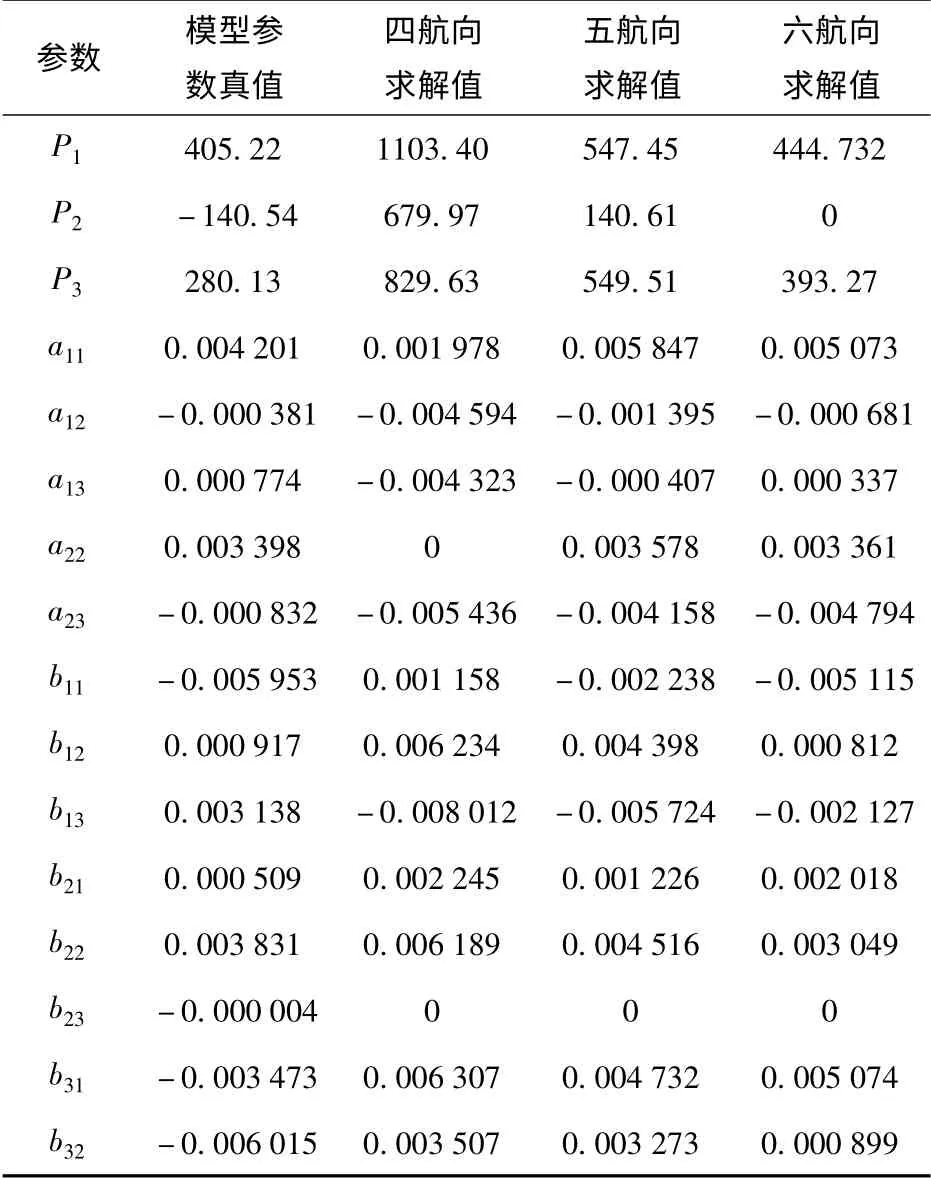
表3 不同航向数计算的飞行器背景磁场模型参数Tab.3 The calculated parameters of aircraft’s magnetic field for different numbers of study lines

从求解的结果可以明显的看出，当增加航向数时，模型参数的求解值更加接近于真实值，另外分别将表3中的四航向求解值，五航向求解值与表1中的第1 组求解值、第2 组求解值相比较可知，在航向数相同的情况下，航向越相互垂直，求解的模型参数也更接近于真实值。

在实际飞行过程中，当学习航向较为接近时，建立的学习方程组具有较强的复共线性，这样对精确求解方程组不利，因而学习时尽量要求学习航向相互正交，但通过上述仿真可知，当飞行器机动性能受限时，在精度允许的情况下，通过提出的折线飞行方法，适当增加学习航向同样可以达到学习求解模型参数的目的。

实际上从Tolles-Lawson 模型以及小信号模型的求解过程可知，提高模型求解的精度关键在于获取的学习数据是否充分。增加航向数可以增加有效的学习数据样本，关于俄罗斯采用的圆周飞行的学习路径可以猜想是否为特定转向角下的无穷多个航向的学习数据样本的叠加。但这种猜想还缺乏依据。

上述仿真研究了航向数目和航向间的角度对模型求解精度的影响，为了研究航向误差对补偿精度的影响，仿真产生航向为5°、85°、175°、285°的学习数据样本，计算出模型参数并与利用标准四航向0°、90°、180°、270°学习样本计算的模型参数进行对比。事实上，前一组航向可以认为是在标准四航向上产生了5°的航向偏差，之所以选取5°，是考虑到飞行器做机动的角度一般小于6°. 表4和表5分别列出了标准四航向以及误差航向下的模型参数计算值与均方根误差。从计算结果来看，当航向偏差在5°以内时，与原来设定的航向相比，模型参数的偏差不大。分析原因，从模型自身的求解来看，只要获取的数据相关性较小，航向偏差对模型求解的精度造成的影响也会较小。

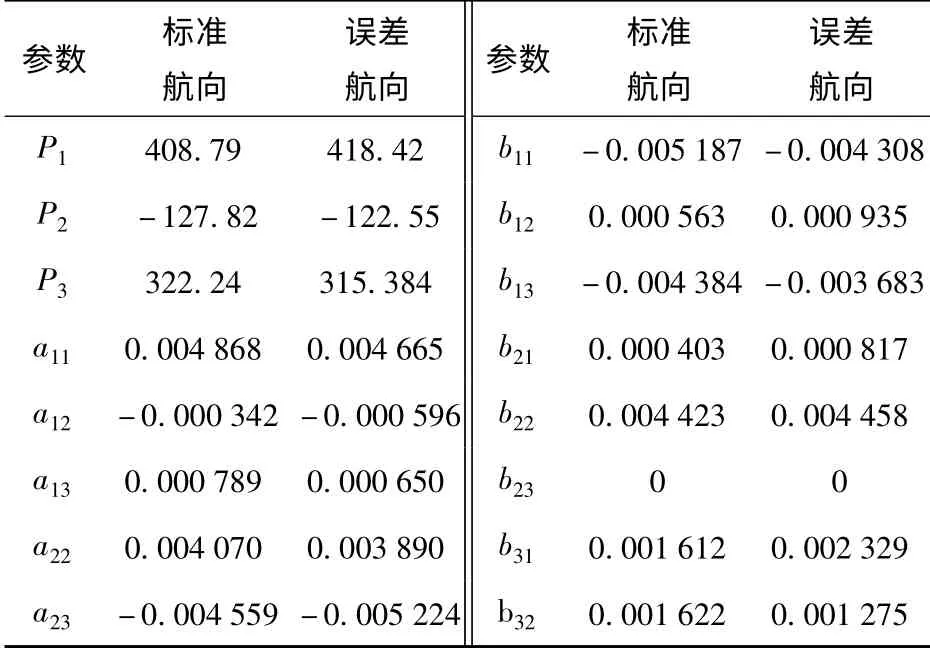
表4 标准航向与误差航向下计算的模型参数Tab.4 The calculated parameters under precise courses and courses with error

为了进一步验证提出的折线飞行方法能否达到学习求解模型参数的目的，选取航磁测绘时的实际飞行数据求解模型参数。飞机在学习飞行时在同一块区域先后进行了图1所示的0°、90°、180°、270°以及45°、135°、225°、315°两组四航向的学习飞行，分别利用0°、90°、180°、270°四航向学习数据与0°、45°、90°、135°、180°五航向的学习数据进行模型参数的求解，图7给出了一段实际航测数据的补偿结果。

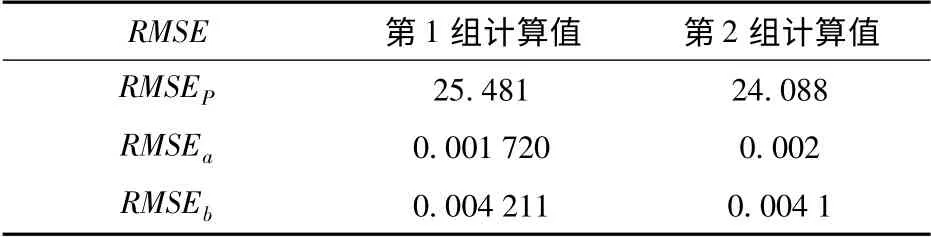
表5 标准航向与误差航向下计算的模型参数均方根误差Tab.5 RMSE of calculated parameters under precise courses and courses with error

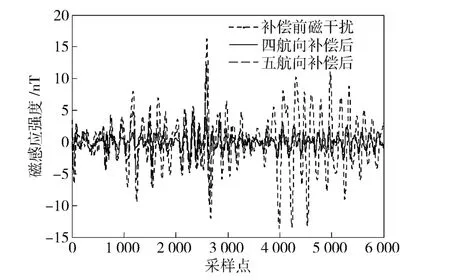
图7 实测飞机背景磁场的补偿Fig.7 Compensation of real aircraft’s magnetic field

从补偿结果可以看出，五航向补偿效果与四航向补偿效果接近，可以达到较好的补偿效果，补偿后的磁干扰幅值基本上在10 nT 以内，且局部区域，五航向的补偿效果甚至优于四航向的补偿效果。

综合仿真实验数据与实际飞行数据，在精度允许的情况下，飞行器可以通过折线飞行路径达到学习飞行的目的。

5 结论

本文针对无人飞行器在模型求解前的学习飞行问题，在Tolles-Lawson 模型的基础上考虑了地磁梯度的影响并提出了一种折线飞行的学习方法，并对学习路径进行了规划。对不同折线飞行路径下模型参数的求解与补偿效果进行了仿真实验与实测飞行数据的验证，得到以下结论:

1)折线飞行路径可以达到学习飞行的目的，求解的模型参数能够较好地补偿飞行器的背景磁干扰。

2)在折线学习飞行时，增加航向数有利于模型参数的精确求解。

3)在航向数相同的情况下，学习航向越相互垂直，模型参数求解的精度越高。

References)

［1］张昌达. 航空磁力梯度张量测量—航空磁测技术的最新进展［J］. 工程地球物理学报，2006，3(5):354 -361.ZHANG Chang-da. Airborne tensor magnetic gradiometric-the latest progress of airborne magnetometric technology［J］. Chinese Journal of Engineering Geophysics，2006，3(5):354 -361. (in Chinese)

［2］杨小军，施坤林，汪仪林. 基于磁传感器/GPS 组合制导飞行弹体的姿态和位置估计［J］.兵工学报，2008，29(2):169 -173.YANG Xiao-jun，SHI Kun-lin，WANG Yi-lin. Estimate of attitude and position of flying projectile controlled by combined guidance based on magnetometer/GP［J］. Acta Armamentarii，2008，29(2):169 -173. (in Chinese)

［3］蔡洪，郭才发，胡正东. 惯性/地磁组合导航算法［J］. 中国惯性技术学报，2009，17(3):333 -337.CAI Hong，GUO Cai-fa，HU Zheng-dong. Algorithms for inertial/geomagnetic integrated navigation［J］. Journal of Chinese Inertial Technology，2009，17(3):333 -337. (in Chinese)

［4］Tolles W E，Lawson J D. Magnetic compensation of MAD equipped aircraft，201-1［R］. Mineola，New York:Airborne Instruments Laboratory Inc. 1950.

［5］Tolles W E. Compensation of induced magnetic fields in MAD equipped aircraft［R］. US:Airborne Instruments Laboratory，OSRD，1943:1386.

［6］Bickel S H. Small signal compensation of magnetic fields resulting from aircraft maneuvers［J］. IEEE Transactions on Aerospace and Electronic Systems，1979，15(4):518 -525.

［7］何敬礼. 飞机磁场的自动补偿方法［J］. 物探与化探，1985，9(6):464 -469.HE Jing-li. Automatic compensation technique for the aeromagnetic field［J］. Geophysical and Geochemical Exploration，1985，9(6):464 -469. (in Chinese)

［8］John J，Bob L，Ross G. Final report on improved aeromagnetic compensation for OMET program［R］. Canada:PetRos EiKon Inc，2004.