绕平头回转体空穴的发展及脱落特性研究
胡常莉,王国玉,陈广豪,王复峰,赵静
(北京理工大学 机械与车辆学院,北京100081)
0 引言
当液体内部的局部压强降低到液体的汽化压强以下时,在液体内部或液固交界面上就会产生包含蒸汽或气体的空穴(空泡),这种现象称为空化。空化现象是航行体水下航行过程最重要的相关流动现象之一[1],它直接影响航行体的水动力特性及操纵稳定性。研究回转体的空化对工程实际应用具有重要的意义。
多年来,国内外学者对回转体的空化流动进行了广泛研究。Rouse[2]等通过实验研究得到了回转体表面压力分布情况,并为数值计算模型的评价提供了可靠的数据。May[3]研究了自然及通气空化状态下的回转体的动力特性并分析了动力脉动及特征频率与空泡形态之间的关系。刘桦等[4]采用高速摄影技术对1/4 平头轴对称体的空泡形态进行了实验研究,发现空泡形态的断裂会产生低频脉动现象。数值计算方面,文献[5 -6]的研究表明湍流模型对于空化流动的预测有十分重要的影响。Johansen等[7]提出基于标准k-ε 模型和大涡模拟的滤波器模型(FBM),文献[8]应用FBM 模型计算了绕圆盘空化器的超空化流场,研究了流场结构及水动力特性。Girimaji 等[9]提出了一种混合RANS/LES 的局部时均化湍流模型(PANS),Frendi 等[10]用PANS 和DES模型预测了后台阶跌坎的湍流流动,发现在相同的网格尺寸和边界条件下PANS 模型的计算结果更精确。文献[11 -13]构建了不同空化模型源相来描述空化流动中的汽液相间传输速率,这种基于质量传输方程的空化模型广泛应用于空化流动数值计算中。
为了深入地了解绕平头回转体的空化流动特性,本文综合运用实验及数值计算的方法,研究了不同空化数下绕平头回转体空穴的发展及空泡的脱落特性,对比分析了不同空化数下空穴的发展过程及脱落细节。
1 实验设备及方法
实验在一循环式空化水洞中进行,如图1所示,空化水洞系统主要由蓄水池、稳流除气罐、电机及调速系统、轴流泵、真空发生装置、实验段及管路组成。实验段截面为0.19 m × 0.07 m 的矩形,长度为0.7 m. 通过其上下部及前侧面的透明有机玻璃窗观察空泡形态。实验中空化数的定义为
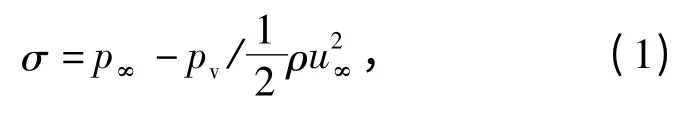
式中:p∞、u∞、ρ 和pv分别为距实验段上游入口210 mm处参考断面上的平均静压强、断面平均速度、水的密度和汽化压强。实验时,保持流速为8.5 m/s,其对应的雷诺数Re=1.7 ×105,通过真空泵调节参考断面的压强进而调节空化数。
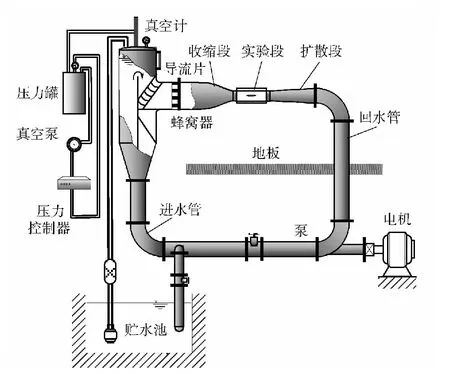
图1 空化水洞示意图Fig.1 Schematic diagram of cavitating tunnel
图2为高速全流场显示系统布局示意图。流动显示实验时,采用3 台1.2 kW 镝灯照明,高速摄像机记录流场中空化形态的演变历程,采集速度设置为5 000 帧/s.
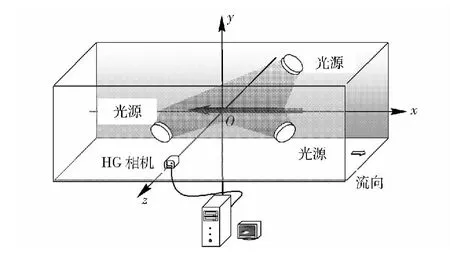
图2 高速全流场显示系统布置图Fig.2 Layout of high-speed video camera system
2 控制方程和数学方法
2.1 基本方法
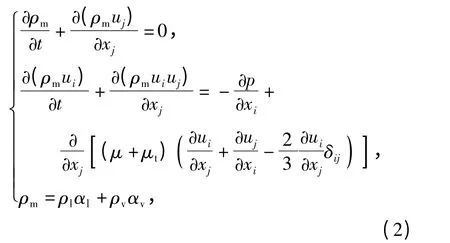
采用均质平衡流模型,汽液两相混合物的连续性方程和动量方程:式中:下标i 和j 分别代表坐标方向;ρm、u 和p 分别为混合密度、速度和压强;μ 和μt分别为混合介质的层流和湍流黏度;ρl、ρv分别为水的密度和水蒸汽的密度。
2.2 湍流模型
本文中采用PANS 模型[9]对湍流流动进行求解。PANS 模型的湍动能ku和耗散率εu的输运方程分别为
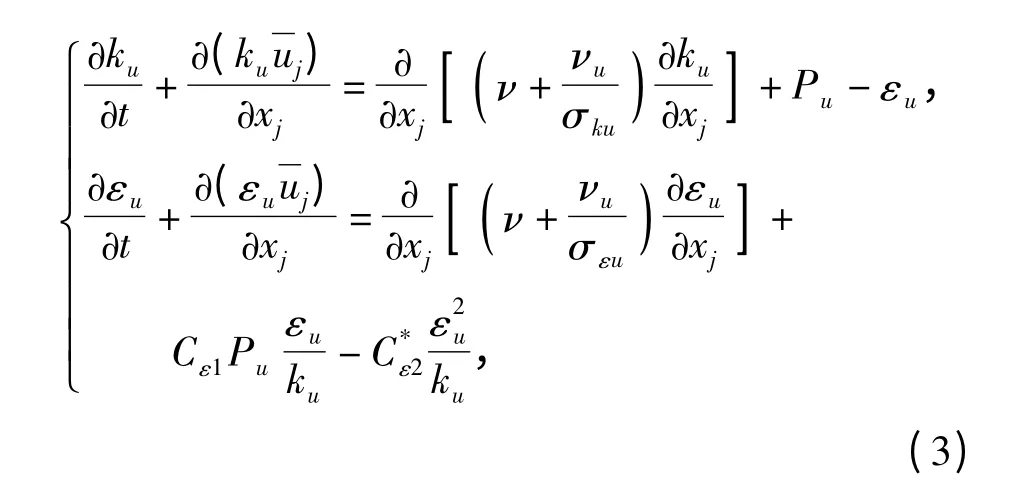
式中:Pu、εu分别为湍动能的产生项和耗散项。湍动粘度:

与标准RANS k-ε 两方程比较,在PANS 模型中,主要对耗散系数C*ε2做出了如下修正:
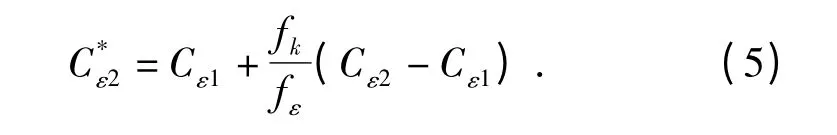
在高雷诺数的流动中,fε值通常取1. 当fk=1时,说明湍流控制方程复原到RANS 模型;当fk=0时,表示数值计算过程没有湍流模型的引入,为直接求解的方式。本文通过对现有软件的二次开发,嵌入了此模型。
2.3 空化模型
空化流动计算中,选用Kubota 空化模型[13],其表达式如下:
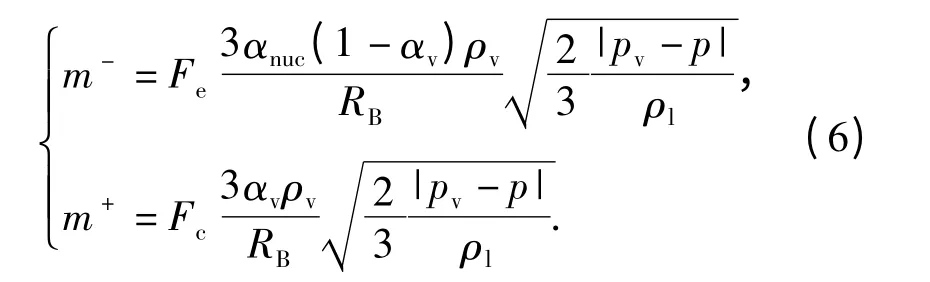
式中:RB为简化气泡半径;pv为汽化压强;ρl、ρv分别为液体密度和蒸汽密度;αnuc为气核的体积分数;Fe和Fc分别是蒸发和凝结常数项。Kubota 空化模型重点考虑了空化初生和发展时空泡体积变化的影响,适于模拟空化的非定常特性。
2.4 计算边界条件及设置
计算采用与实验几何尺寸相同的模型。计算区域及边界条件设置如图3所示,边界条件设置为速度进口和压力出口,流动区域的上下左右边界采用自由滑移壁面条件,平头回转体表面采用绝热、无滑移固壁条件。
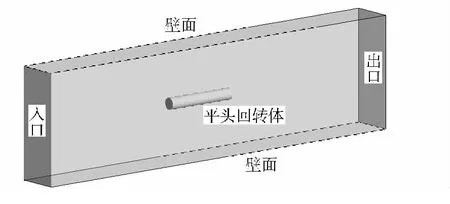
图3 计算域及边界条件Fig.3 Computational domain and boundary condition
图4给出了平头回转体及其一个纵向切面的网格图。为了更准确计算空化流动,在平头回转体周围近壁区域进行了网格加密,近壁面y+值为20 ~100,满足壁面函数要求。回转体的前端采用O 型结构的网格,这样可以较好地匹配平头回转体头部的形状。数值计算的空化数及雷诺数大小均与实验值保持一致。

图4 平头回转体及其纵切面网格Fig.4 Grid of blunt body and its longitudinal section
3 实验结果与讨论
3.1 空穴的发展特性
图5(a)和图5(b)分别给出了σ=0.9 时,由高速录像和数值计算得到的不同时刻的空穴形态变化。图5(b)中同时给出了相应的回转体表面压力分布云图。从图5(a)中可以看出,空穴为由环绕在回转体的头部附近小尺度的空泡团组成。在该空化条件下,空穴的发生在位于距肩部约0.2D ~1.5D的范围内(D 为回转体直径);在周向上空穴并没有完全包裹回转体。结合图5(b)可知,聚集状的空泡团发生在回转体头部的低压区域,且该区域的压力分布呈现明显的非定常性。实验及数值结果均发现,该工况下空穴的发展过程并没有明显的周期性,且空泡团的脱落现象表现为尾部小尺度空泡团的瞬时溃灭消失。

图5 瞬时空穴形态图(σ=0.9)Fig.5 Evolution process of cavity with time (σ=0.9)
为了说明空化进一步发展阶段空穴随时间的变化情况,图6和图7分别给出了σ =0.7 与σ =0.6时,空穴形态在其一个发展周期内的演变过程。相比于σ=0.9 时的空穴形态,发现这两个工况下的空穴向回转体的头部发展并呈附着状,另外,由于空化数的降低,空化得以进一步发展,空穴形态均以大尺度空泡团的形式包裹着整个回转体的头部区域,同时进行着规律、周期性的演变:开始时,空穴呈椭球状,较稳定地包裹着回转体头部;随后,空穴表面开始凹陷;当t0+ 4.4 ms 时,在距回转体肩部约0.3D 的位置处,空穴断裂;然后,空穴尾部出现空泡团逐渐脱落的现象;最后,空穴又覆盖了回转体的头部区域,此时空穴形态便完成了一个周期的变化过程。虽然这两个工况下的演变过程基本相同,然而仔细对比图6和图7则可发现二者存在明显的差异:其一,当空穴断裂之后,σ=0.7 时的空穴几乎完全被一分为二,而σ =0.6 时的空穴在一定时间后又重新融合在了一起;其二,这两个工况下空穴发展的准周期分别为15.4 ms 和37.4 ms,即σ =0.6 时的发展周期更长些且空穴可以在较长的时间内稳定地包裹着回转体头部而不出现大尺度空泡团的脱落现象。

图6 空穴形态随时间的演变(σ=0.7)Fig.6 Evolution process of cavity with time (σ=0.7)
3.2 空泡的脱落特性
空穴的断裂与空泡的脱落特性是研究非定常空化问题的关键。从3.1 节的研究中发现,在不同空化数下,绕平头回转体的空泡脱落过程是不同的。为了进一步研究绕平头回转体空泡的脱落特性,本节将先后讨论σ=0.7 和σ=0.6 时,空泡的脱落过程及其特点。

图7 空穴形态随时间的演变(σ=0.6)Fig.7 Evolution process of cavity with time (σ=0.6)
表1中分别给出了σ =0. 7 时,由实验及数值计算得到的空泡脱落细节,其中,实验结果共列出了A、B、C 3 组不同的空泡脱落过程,数值计算结果同时给出了回转体的表面压力分布云图。从表1中可以看出,实验结果及数值计算结果比较一致地展示出了空泡脱落的全过程:空穴断裂—裂痕前面附着空穴逐渐增长—裂痕后面大尺度空泡团翘起并逐渐脱落。对比由实验得到的A、B、C 3 组结果可知,空穴断裂的位置基本相同,即位于距回转体肩部约为0. 3D 的位置处,且空穴断裂为U 型涡状。

表1 空泡脱落细节(σ=0.7)Tab.1 Details of cavity shedding (σ=0.7)
图8统计了表1中A、B、C 3 组空穴断裂位置随时间的变化情况及脱落空泡的运动速度。统计时,始终以断裂处后面的某一定点为统计对象。3 条位置曲线可以反映出脱落的空泡随主流的运动情况,结合其速度曲线可知,空泡脱落的速度随时间是波动变化的,其波动范围为0 ~1.8u0(u0为来流速度),它们的平均速度约为0.6u0. 由表1中空穴的裂痕随着时间的推移而逐渐变宽的趋势可推测出,裂痕前面的附着空穴增长的平均速度小于0.6u0.
类似地,图9给出了σ =0.6 时,空泡的脱落细节图。从图9中可以发现,空穴断裂的位置也位于距肩部约0.3D 处。当t0+0.8 ms 时,空穴裂痕增大且与回转体轴线呈一定的角度。随着时间推移,由于裂痕上游的空穴发展较快,裂痕逐渐模糊,裂痕前后的空泡团逐渐融合在一起。当t0+2.0 ms 时,空穴的下游处又发生空穴断裂,之后,断裂后的两部分空穴再次融合。正是这种“断裂”又“融合”的作用,抑制了大尺度空泡团的卷起及脱落现象,取而代之的是小尺度空泡团在空穴尾部脱落溃灭。图10给出了另一组空穴的断裂及融合的演变过程,从图10 中可以清楚地看到,与σ =0.7 时相类似,在反向射流的作用下空穴的断裂亦呈U 型涡状。
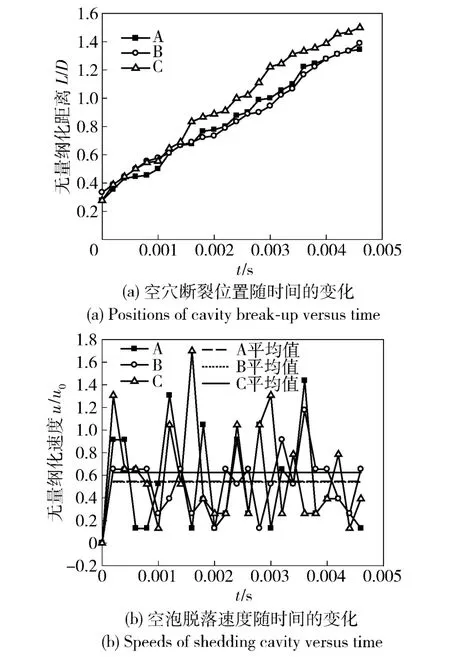
图8 空泡脱落过程及脱落速度随时间的变化情况(σ=0.7)Fig.8 Change of cavity shedding and its velocity with time

图9 空泡脱落细节(σ=0.6)Fig.9 Details of cavity shedding (σ=0.6)

图10 空穴断裂与融合(σ=0.6)Fig.10 Cavity shedding and its amalgamation (σ=0.6)
空泡的脱落特性与流场中的反向射流是密切相关的,为了研究反向射流对空穴的作用,图11给出了空化数σ=0.6 时,在反向射流的作用下空穴的发展情况,同时给出了计算获得的回转体的表面压力分布云图及其一个纵切面上的速度矢量分布图。结合空穴形态及回转体的表面压力分布情况可知,在空穴闭合区域的后面存在较大的逆压区域,尤其是最长空穴的后面对应着局部高压区,此处会首先诱导一股反向射流,随着时间推移,空穴尾部的高压区逐渐沿回转体的周向方向扩展,同时结合速度矢量分布图可知,反向射流也逐渐增强,导致空穴不断回缩。由空穴形态图可以看出,回转体周向各点的反向射流向前推进的速度是不同的,导致空穴断裂呈U 型涡状,这一特点与实验观测的结果相一致。

图11 反向射流推进过程(σ=0.6,上图为空泡形态与压力云图,下图为速度矢量与压力云图)Fig.11 Development of re-entrant jet (σ=0.6,the images above are cavity shapes and pressure contours,the images below are velocity vectors and pressure contours)
4 结论
本文采用高速录像方法和数值计算方法研究了绕平头回转体的空穴发展及空泡脱落特性,所得结论如下:
1)绕平头回转体空穴的发展过程和空泡的脱落细节均受空化数的影响。空化数较大时,空穴的发展及脱落过程没有准周期性;随着空化数的减小,空穴的发展及脱落过程具有明显的周期性。研究发现,空化数越小,空穴的发展周期越长,脱落的空泡尺度越小。
2)绕平头回转体的空泡准周期性脱落过程主要包括空穴断裂与空泡脱落两个过程。统计发现,空穴断裂的位置大约位于距回转体肩部0.3D 处。实验及数值结果均表明,由于反向射流的作用使空穴的断裂呈U 型涡状。
3)在一定的空化条件下,绕平头回转体的空化由于断裂和融合两个过程的存在,将使空穴呈现更加稳定性的特征。
References)
[1]权晓波,李岩,魏海鹏,等.大攻角下轴对称航行体空化流动特性试验研究[J]. 水动力学研究与进展,2008,28(6):662 -667.QUAN Xiao-bo,LI Yan,WEI Hai-peng,et al. An experiment study on cavitation of underwater vehicle’S surface at large angles of attack[J]. Chinese Journal of Hydrodynamics,2008,28(6):662 -667.(in Chinese)
[2]Rouse H,McNown J S. Cavitation and pressure distribution,head forms at zero angel of yaw,studies in engineering[R]. Bulletin:State University of Iowa,1948:32.
[3]May A. Water Entry and the Cavity-Running Behavior of Missiles[R]. Silver Spring:Naval Sea Systems Command Hydroballistics Adcisory Committee,1975.
[4]刘桦,何友声,赵岗. 轴对称空泡流的脉动性态研究[J]. 上海力学,1997,18(2):99 -104.LIU Hua,HE You-sheng,ZHAO Gang. A study on pulsation of axisymmetric cavitation flows[J]. Shanghai Journal of Mechanics,1997,18(2):99 -104. (in Chinese)
[5]Wu J,Wang G Y,Shyy W. Time-dependent turbulent cavitating flow computations with interfacial transport and filter based models[J]. International Journal for Numerical Methods in Fluids,2005,49(7):739 -761.
[6]Coutier-Delgosha O,Reboud J L,Delannoy Y. Numerical simulation of the unsteady behavior of cavitating flows[J]. International Journal for Numerical Methods in Fluids,2003,42(5):527-528.
[7]Johansen S T,Wu J,Shyy W. Filter-based unsteady RANS computations [J]. International Journal of Heat and Fluid Flow,2004,25(1):10 -21.
[8]余志毅,王国玉,顾玲燕,等.圆盘空化器超空化绕流流场结构及动力特性的数值分析[J].兵工学报,2008,29(12):1444 -1449.YU Zhi-yi,WANG Guo-yu,GU Ling-yan,et al. Numerical analysis of structure and dynamic characteristics of suppercavitating flow around a disc cavitator[J]. Acta Armamentaii,2008,29(12):1444 -1449. (in Chinese)
[9]Girimaji S,Abdol-Hamid K S. Partially averaged navier stokes model for turbulence:implementation and validation[C]∥The 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reno,Nevada:AIAA,2005:502.
[10]Frendi A,Tosh A,Girimaji S S. Flow past a backward-facing step:Comparison of PANS,DES and URANS results with experiments[J]. International Journal for Computational Methods in Engineering Science and Mechanics,2006,8(1):23 -38.
[11]Kunz R,Boger D,Stinebring D,et al. A preconditioned implicit method for two-phase flows with application to cavitation prediction[J].Comput & Fluids,2000,29(8):849 -875.
[12]Singhal A K,Athavale M M,Li H,et al. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering,2002,124(3):617 -624.
[13]Kubota A,Kato H,Yamaguchi H. A new modeling of cavitating flows:a numerical study of unsteady cavitation on a hydrofoil section[J]. Journal of Fluid Mechanics,1992,240(1):59 -96.

