通气空泡内部流动特征数值仿真

仲 霄, 王树山, 马 峰



通气空泡内部流动特征数值仿真

仲 霄, 王树山, 马 峰

(北京理工大学 爆炸科学与技术国家重点实验室, 北京, 100081)

通气条件会造成通气空泡内部压力分布变化, 对空泡壁面产生显著的冲击作用, 进而严重影响通气空泡动力学规律。本文利用FLUENT软件进行了通气空泡内部气体流动结构的数值仿真, 并通过数字图像粒子测速(DPIV)试验数据和高速摄影试验数据对数值模型进行联合标定, 分析了不同通气条件对空泡内部气体流动结构的影响规律。仿真结果表明, 通气条件对射流区的流动形态影响较大, 对回流区影响较小; 通气角影响射流区的流动结构, 通气量影响射流区和回流区在空泡内部所占比例。

通气空泡; 内部流动; 通气条件; 数值仿真

0 引言

通气空泡技术是借助人工通气手段降低空泡产生的阈值条件, 在较低相对速度条件下实现空泡乃至超空泡现象的技术, 是如今方兴未艾的高速水下航行器研究实现超空泡减阻的主要技术途径之一, 也是作为水动力学重要分支的空泡动力学基础研究的主要试验技术之一。

需要指出的是, 人工气流固然降低了空泡产生的难度, 使得空泡动力学基础试验研究和超空泡减阻工程技术更容易实现, 但新物质的介入及其动力学作用产生的影响不可忽视: 一方面, 人工通入空泡的高速气流在空泡内部的有限空间内形成复杂的流动结构, 该流动结构与周围水介质产生动力学作用, 为空泡壁面提供支撑作用的同时也会对空泡壁面产生不可避免的扰动作用; 另一方面, 对于采用超空泡减阻技术的高速水下航行器工程研究来说, 空泡壁面与其内部的复杂气体流动结构构成高速水下航行器的主要力学环境, 对航行器的运动规律乃至运动控制都产生直接影响。因此, 通气空泡内部流场的流动结构特征及其动力学规律研究是空泡动力学基础研究和超空泡减阻工程技术研究不可回避的问题之一。

目前对空化流场的理论研究还主要是以Reichardt[1]、Tulin[2]和Loginovich[3]等前人建立的理论模型为基础, 以假定空泡内部压力为常数或预置内外压变化来研究空泡壁面的形态变化规律为主要特点, 而考虑空泡内部气体真实流动规律的空泡动力学理论模型还是空白。造成这种现象的主要原因是对于空泡内部流动结构的试验认识严重缺失。

对于试验来说, 由于介入式测试会对空泡流场产生严重干扰, 目前, 空化流场试验研究可用的技术手段主要是基于空化水洞的高速摄影技术, 能够对空泡形貌及其发展规律进行直接观测, 而对空泡内部的流动特征缺乏判读上的依据。数字粒子图像测速(digital particle image velocimetry, DPIV)试验方法能够以示踪粒子的方式直接获取流场速度的分布特性和流动结构, 是目前流体力学研究的新兴试验技术, 北京理工大学目前已经开始将DPIV测试手段用于直接观测空泡内部流动结构[4-5], 鉴于试验量和数据分析的难度, 获得对于空泡内部真实流动结构的全面试验认识尚需时日。

数值仿真是目前科学研究的主要手段之一, 其主要优点在于经济性、方便性以及数据结果体系的全面性, 但需进行针对性的试验标定以保证数值仿真模型与结果的可靠性。目前国内外对于空化流场数值仿真模型的研究与成果很多, 但大多关注于数值模型算法[6]、超空泡形态与控制规律、航行器的水中运动阻力特性[7-9]等方面, 涉及空泡内部流场的流动特性及其影响规律的数值仿真研究较少。究其原因还是在于仿真研究缺乏试验规律的支撑, 数值仿真结果可靠性无法保证。

本文利用FLUENT流体动力学数值仿真软件进行研究, 并通过DPIV试验数据和高速摄影试验数据对数值仿真进行联合标定, 获得了可靠的通气超空泡内部气体流场的流动结构仿真数据, 并对通气条件的影响规律进行了分析。

1 数学模型

计算采用无滑移速度的混合多相流模型, 模型计算所采用的基本方程如下。

1) 连续性方程

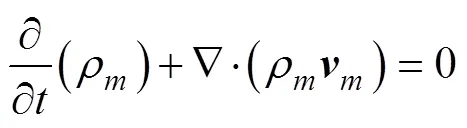
2) 动量方程

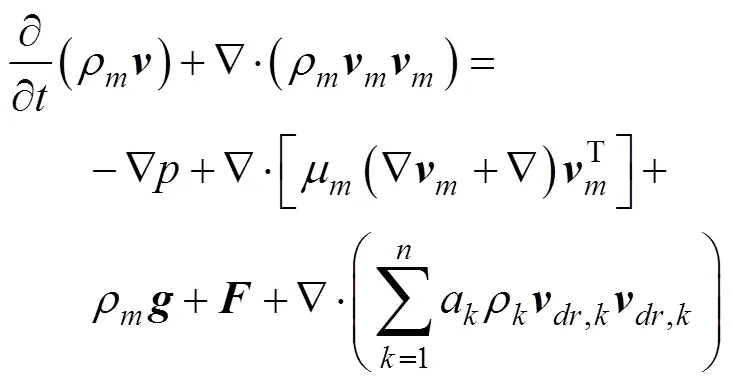
3) 湍流方程

数值仿真计算采用Realizable湍流模型, 模型所采用的输运方程表达式如下

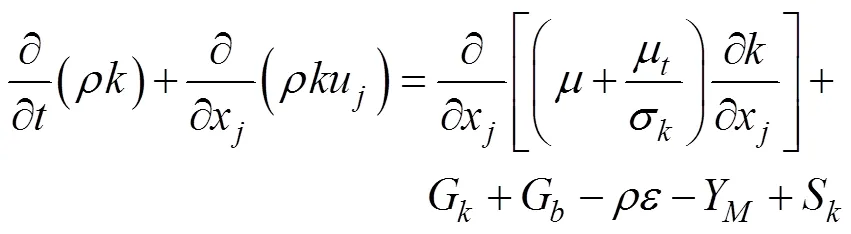
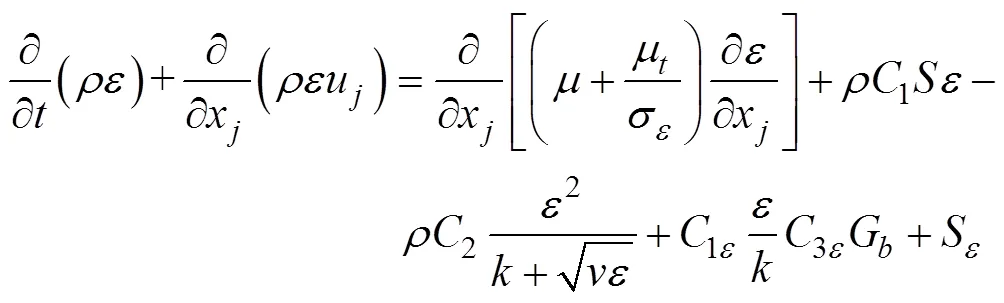
4) 几何模型与计算网格

计算流场区域为全长400 mm, 直径100 mm的四分之一圆柱体, 航行体位于圆柱体中心, 航行体头部距离流场入口40 mm, 航行体轴线平行于来流方向。航行体外形和几何尺寸如图1所示, 计算网格为TrueGird生成的结构化网格, 网格使用六面体单元进行划分, 并对近壁面网格进行加密处理, 最小网格单元尺寸为0.2 mm, 计算区域网格总数为5.5×105, 网格划分如图2所示。

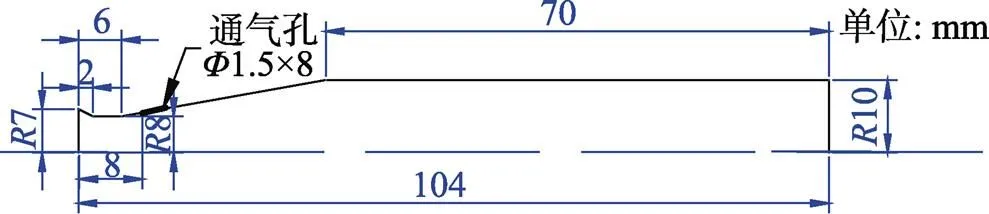
图1 航行体几何尺寸

图2 计算网格示意图

5) 数值方法

采用压力耦合方程组的半隐式方法(semi- implicit method for pressure linked equations, SIMPLE)实现压力与速度场的耦合求解。航行体上游为速度进口, 下游为压力出口, 壁面及外侧壁面采用无滑移边界条件, 对近壁面网格采用标准壁面函数处理, 通气口采用质量流量边界。

由于本文主要讨论通气条件对空泡内部流场的影响, 因此本文主要在给定的来流速度和环境压力的情况下, 研究通气方向和通气量大小对内部流场结构的影响。为便于描述通气方向, 取航行体头部中心为原点, 航行体轴线指向尾部方向为轴线正向, 则定义通气方向与空化器轴线之间的夹角为通气角(如图1所示); 通过定义无量纲系数通气率来表示通气流量影响。本文中所提到的无量纲系数有雷诺数, 自然空化数以及通气率系数, 其定义为

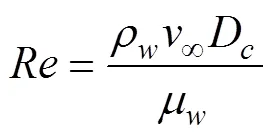
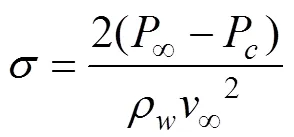
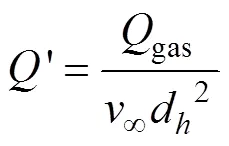
式中:ρ为水的密度;为来流流速; 取航行体的头部圆盘空化器的最大直径D为特征长度;μ为水的动力学粘度;为环境压力;P为水的饱和蒸汽压力,gas为通气体积流量。

2 计算结果与讨论

2.1 空泡内部流动基本特征及试验标定

利用上述数学模型建立基于FLUENT的数值仿真模型, 进行了通气参数对于空泡内部气体流动结构的影响规律仿真分析, 数值分析设定工况为: 雷诺数=9248, 自然空化数=1.48, 通气率分别为0.3258, 0.4316, 0.8143和通气角分别为30°, 45°, 90°, 135°。取计算流场中通过航行体轴线和通气孔轴心的截面所在的2D空间流场进行比较和分析。

采用已得到的相同工况DPIV试验数据和高速摄影试验[4]图像与数值仿真结果进行对比分析, 实现对仿真模型的验证与标定, 如图3所示。通过对比发现, DPIV试验获得的流场结构试验图像(图3b)中, 气流运动方向在空泡内部发生了转变, 这一现象特征及位置与数值仿真的结果(图3a)是一致的。同时对比高速摄影图像(图3c)发现, 空泡内部尾部射流所能达到的位置也与DPIV和数值仿真结果中的气流转向位置相一致。因此, 本文将高速摄影图像中可观测尾部回射流的边界作为空泡内部气体流动结构的典型示踪特征来进行研究。

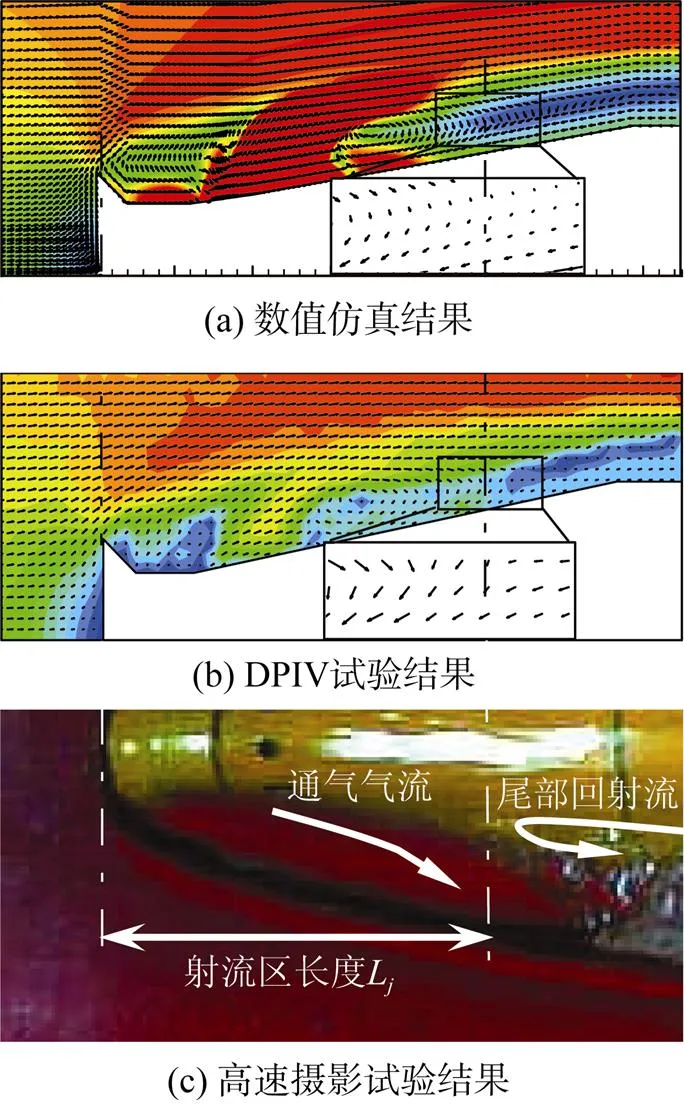
图3 数值仿真、数字粒子图像测速试验与高速摄影试验结果比较

图3a为通气角度=45°, 通气率=0.8143时空泡流场的流速矢量图和速度云图。由图中流速矢量图可见, 空泡中后部流动以尾部射流形态为主, 空泡的头部区域以气体射流流动形态为主, 在射流以外的区域由于气体的剪切运动, 在空泡头部形成了大小和强度不同的涡旋。因此按照流动特性将空泡内部流场分为2个区域: 头部区域由于内部气流形态主要受高速通气气流影响, 其流动类似于气体射流, 称之为射流区; 空泡中后部区域流动形态以漩涡运动为主, 并伴随着尾部回射流的存在, 称之为回流区。由于空泡流场的非定常性, 因此对测得的射流区长度进行多次测量并进行时均处理, 以此测得射流区长度L和空泡长度L。在数值仿真结果中,L取空化器头部驻点到空泡内部头部射流区和尾部回流区的分界点之间的轴向距离, 其中, 由于头部射流区和尾部回流区在空泡轴线方向上存在重叠, 因此头部射流区和尾部回流区分界点取射流区和回流区重叠区域的中心点位置; 获取L时, 取流场中气体相体积分数gas＝0.8作为数值仿真中空泡壁面位置和空泡长度的判定条件。

图4为数值计算和水洞试验获得的L和长度比值L/L的比较, 可以看出, 数值计算获得的长度比值和水洞试验结果大致符合, 试验测得的L和L/L略大于数值计算结果, 这是因为试验中空泡内部气流受到了航行体内部通气管路设计的影响, 使得试验中实际通气方向更贴近于航行体壁面, 使射流区的气体对尾部射流的阻碍作用增强, 导致试验中观测到的射流区长度略大于数值计算的射流区长度。

2.2 通气条件对空泡内部流动特征的影响

表1为不同通气角和通气率下通气空泡的内部气体体积分数云图和流线。由表可见, 通气角对内部流场结构特性有着显著的影响: 当=30°时, 气流从通气口流出并与尾部回流气体在射流区和回流区交界形成正面冲击; 而随着的增加, 气流的撞击位置也相应发生变化, 使得通气孔气体与回流的撞击作用减弱, 气体射流开始逐渐远离航行体表面, 头部气体射流区的尺寸随之减小;=45°时, 通气口出流气体与回流区不再形成正面冲击, 尾部回流流向通气口出流气体内侧, 之后在通气口出流气体的影响下流向空泡壁面, 并沿空泡壁面流向空泡尾部; 当通气气流与航行体轴线正交时, 即通气角=90°时, 通气孔出流气体直接对空泡壁面发生碰撞; 随着通气角度进一步增加, 当通气角=135°时, 头部气体射流区的尺寸进一步缩小, 同时存在于头部气体射流的流动方向开始与尾部回流趋于一致, 头部气体射流区的流动状态趋于均匀, 射流区和回流区的流动开始融合。

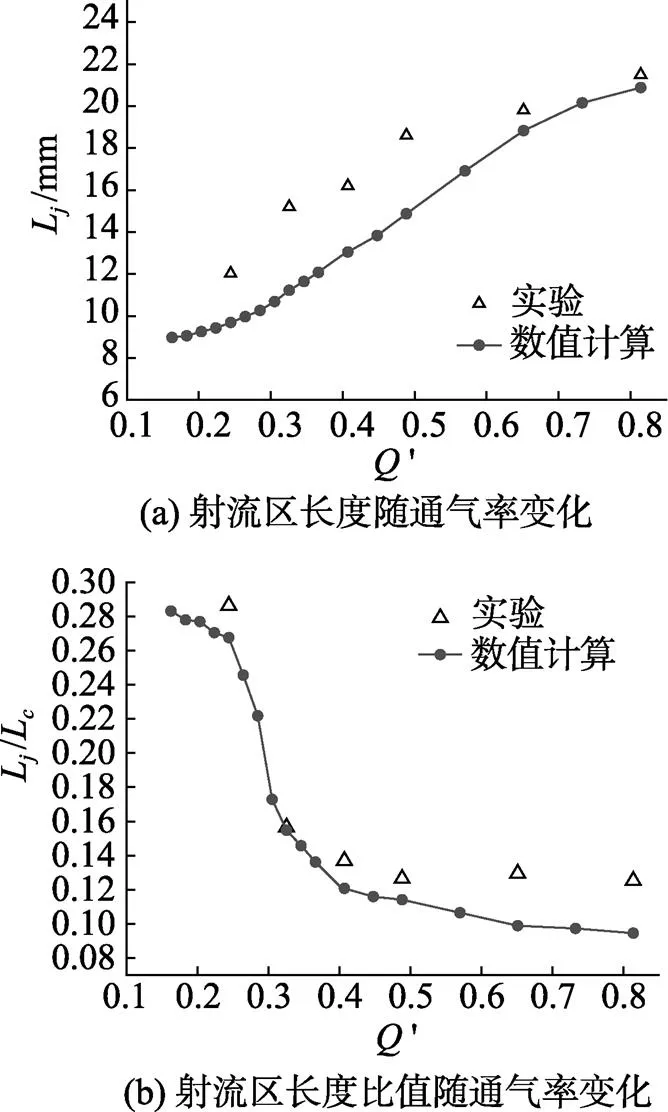
图4 数值计算结果与水洞试验结果比较

Fig 4 Comparison between the results of calculation and water tunnel experiment

从不同通气量下空泡内部的流动特性可以看出, 通气量主要影响到头部气体射流区尺寸、空泡几何尺寸以及回流区内气体体积分数, 通气率的改变并未导致通气孔出流和回流碰撞作用的变化, 碰撞位置一直保持在航行体表面附近, 因此空泡内部流动特征并未改变。由于＞90°后, 射流与尾部回流的方向开始趋于一致, 射流区和回流区的分界面逐渐消失, 因此仅对≤90°时空泡内部射流区长度L和比值L/L进行测量。

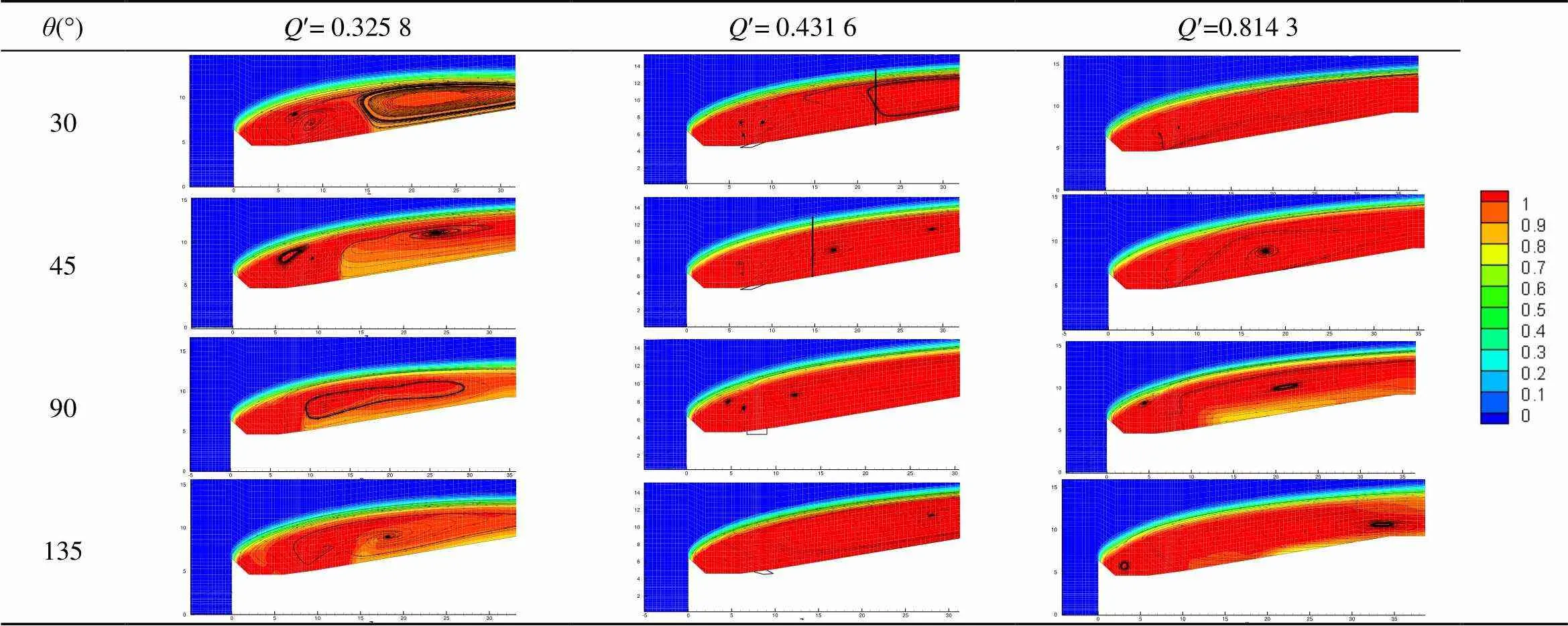
表1 不同通气条件下通气空泡内部流场流动特性

图5为测得的L和L/L随通气率的变化规律, 由图5可以看出, 当通气角为30°或45°时,射流区长度均随着通气率的增加而增长。由于通气角的增加导致内部气体流速轴向分量的减小, 因此通气角=30°时射流区的长度大于通气角=45°时的长度; 当射流区分界超过航行体的圆锥段后, 由于空泡截面积的减小导致了尾部射流区对流流速的增加, 从而减缓了射流区长度的发展, 因此当射流区分界面超过航行体圆锥段后射流区长度L趋于稳定。

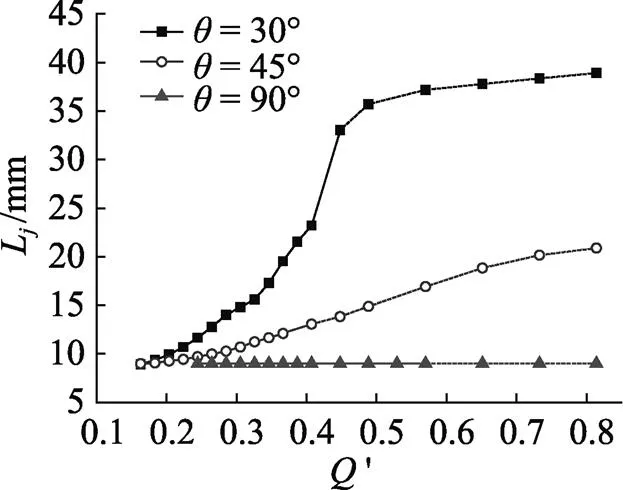
图5 射流区长度随通气率变化规律

图6为不同通气角度下射流区长度比值随通气率的变化规律。由于空泡发展到超空泡阶段后尾部在水流中发生闭合, 空泡尾部闭合机理的不同和空泡在跨越航行体尾部后造成空泡全长的阶跃会对射流区长度比值L/L产生影响, 因此将非超空泡阶段和超空泡阶段的曲线进行分别描述, 图中实线部分表示空泡闭合于航行体表面, 右侧虚线表示空泡已经将航行体完全包裹, 到达超空泡阶段。

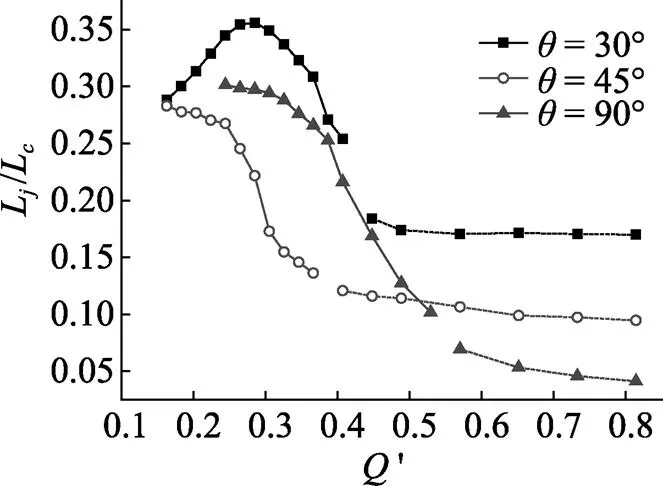
图6 射流区长度比值随通气率变化规律

当=45°时, 通气气流一部分与尾部回流发生接触, 另一部分气流则直接由空泡壁面附近流入回流区, 由于该角度通气的大部分进入尾部射流区, 通气量的增加导致了空泡长度的增加速度高于射流区长度的增长速度, 因此, 随着通气量的增长, 射流区长度比值不断减小。

当=30°时, 由于此时头部气体射流与尾部回流发生直接碰撞, 通气的大部分动能用于射流区的维持, 当通气率较低时, 随着通气量增加, 射流区的增长速度较快, 而空泡由于在航行体的斜面处闭合, 在发展过程中受到较大的阻碍作用而增长较慢, 因此, 射流区长度比值在这一区域随通气的增加而增长, 当通气量增加到一定程度后, 空泡尾部发展到圆柱段, 由于尾流区在航行体表面受到阻力减小, 使得尾流区开始向后部发展, 因此, 射流区的长度比值开始逐渐减小。

当=90°时, 即通气方向与航行体轴线垂直时, 由于通气速度的径向分量的急剧减小使射流区长度缩短, 射流区和尾部射流区的分界面保持恒定, 此时射流区长度的比值与空泡长度成反比。当通气量足够使空泡发展成超空泡后, 射流区长度比值开始趋于稳定, 而且射流区长度比值随着通气角度的增加而减小。

通气方向的不同导致了空泡内部流动特性的差异, 也影响到了射流区的长度和长度比值: 当=30°时, 射流区长度比值相对最高, 这是因为通气的大部分动能都用于维持射流区形态, 而且由于只有很小一部分气体动能作用到尾部射流区, 因此空泡的总长较小; 当增加到45°时, 由于部分气体开始直接流入尾部射流区, 使得射流区尺寸开始减小, 而空泡的长度由于尾部射流区气体动能的增加而增长, 因此射流区长度比值远远小于30°时; 而随着通气角的进一步增加, 进入尾部射流区气体的流速的轴向分量开始逐渐减小, 使得尾部射流区尺寸也随之缩短, 当90°时, 由于空泡全长缩小, 使得在空泡阶段的射流区比例增长, 高于通气角45°时的射流区比例。

由此可见, 通气方向的改变影响了空泡内部气流的流动结构和特性, 这是由于的改变导致了通气孔出流与尾部回流相对位置的变化, 而相对位置的变化则导致了空泡射流区不同流动结构的产生。当通气量足够高时, 由于90°的射流区长度保持不变而空泡全长随通气量的增加而增长, 使得射流区长度比值开始减小, 在超空泡阶段射流区长度比值随着通气角的增加而减小。

3 结论

本文通过数值仿真手段对圆盘头部截锥形通气航行体形成的空泡内部流场结构进行了研究, 得出结论如下。

1) 经过DPIV试验数据与高速摄影图像的联合标定, 本文研究采用的数值仿真模型具备一定的可靠性, 所得仿真数据结果可用于通气空泡内部流动结构分析;

2) 通气空泡内部流场按照流动特性可以分成射流区和回流区2个部分, 射流区的流速较高, 以射流的流动形态为主, 流动结构较为复杂, 回流区的流动特性以旋转运动为主;

3) 射流区的流动形态受通气角度影响, 不同的通气角度会导致射流区流动结构的改变, 通气流量会影响到射流区和回流区的尺寸, 但是不会导致不同流动特征的产生;

4) 通气流量会影响射流区的尺寸和射流区占空泡的比值大小: 当通气量较小时, 通气量对射流区长度及比值的影响较大, 而且由于射流区流动结构的不同, 不同通气角度下通气量对射流区比值的影响规律之间有所区别; 随着通气量增加形成超空泡后, 射流区的增长速率逐渐接近空泡全长的增长速率, 射流区占空泡全长比值趋于稳定。

[1] Stinebring D R, Billet M L, Lindau J W, et al. Developed Cavitation-Cavity Dynamics[R]. RTO AVT Series on “Supercavitation Flows”, AD340843, 2002.

[2] Tulin M P. Cavity Shapes in Three Dinmensions[R]. High Speed Body Motion in Water, ADA340843, 1998.

[3] Loginovich G V. Hydrodynamics of Flows with Free Boundaries[M]. Halsted Press, 1973.

[4] 仲霄, 王树山, 马峰, 等. 通气超空泡内部流场PIV测试方法[J]. 船舶力学, 2013, 17(8): 851-857.

Zhong Xiao, Wang Shu-shan, Ma Feng, et al. A PIV Measuring Method of Flow in Ventilated Super-cavi- tation[J]. Journal of Ship Mechanics, 2013, 17(8): 851-857.

[5] 仲霄, 王树山, 马峰. 通气超空泡内部流场的PIV实验图像处理[J]. 船舶力学, 2013, 17(7): 715-721.

Zhong Xiao, Wang Shu-shan, Ma Feng. PIV Image Processing Method of the Ventilated Super-cavtating Flow [J]. Journal of Ship Mechanics, 2013, 17(7): 715-721.

[6] 时素果, 王国玉, 余志毅, 等. FBM湍流模型在非定常通气超空化流动计算中的评价与应用[J]. 船舶力学, 2012, 16(10): 1101-1106.

Shi Su-guo, Wang Guo-yu, Yu Zhi-yi, et al. Evaluation of the Filter-based Turbulence Model(FBM) for Computation of Unsteady Ventilated-supercavitating Flows[J]. Journal of Ship Mechanics, 2012, 16(10): 1101-1106.

[7] Kunz R F. A Preconditioned Navier-Stokes Method for Two-phase Flows with Application to Cavitation Predic- tion[J]. Computers & Fluids, Elsevier, 2000, 29(8): 849-875.

[8] 熊永亮. 水下航行体超空泡生长规律的数值研究[D]. 哈尔滨工程大学, 2006.

[9] 郝宗睿, 王乐勤, 吴大转. 水翼非定常空化流场的数值模拟[J]. 浙江大学学报(工学版), 2010, 44(5): 1043-1048.

Hao Zong-rui, Wang Le-qin, Wu Da-zhuan. Numerical Simulation of Unsteady Cavitating Flow on Hydrofoil[J]. Journal of Zhejiang University(Engineering Science), 2010, 44(5): 1043-1048.

(责任编辑: 陈 曦)

Numerical Simulation on the Internal Flow Characteristics in Ventilated Cavity

ZHONG XiaoWANG Shu-shanMA Feng

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

The distribution of internal pressure in ventilated cavity is affected by ventilation condition, which may induces distinct impact effects on the boundary of the cavity and the dynamics rules of ventilated cavity. In this paper, the internal flow structure of ventilated cavity is simulated by using CFD code of FLUENT, and the simulation results are calibrated by digital particle image velocimetry(DPIV) and high-speed camera experiments. Then the effects of different ventilation conditions on internal flow structure of cavity are analyzed. Numerical simulation results indicate that the ventilation conditions impose clear influence on the flow form of gas-jetting region and weak influence on the recirculating region, the angle of ventilation affects the structure of gas-jetting region, and the flow rate of ventilation affects the proportion of gas-jetting region and recirculating region to the internal cavity space.

ventilated cavity; internal flow; ventilation condition; numerical simulation

TJ630.1; TV131.32

A

1673-1948(2014)01-0001-06

2013-11-22;

2013-12-16.

爆炸科学技术国家重点实验室基金项目(YBKT09-07).

仲 霄(1985-), 男, 在读博士, 主要从事水弹道学研究.