一种抗海浪扰动实时控制信号滤波方法

赵 江, 肖昌美, 雷霏霖, 江 涛, 王 超



一种抗海浪扰动实时控制信号滤波方法

赵 江, 肖昌美, 雷霏霖, 江 涛, 王 超

(海军装备研究院, 北京, 100161)

为了克服伺服控制系统中滤波效果与系统相位裕度不能兼顾, 消除高频噪声会损失有用低频信号的问题, 以卡尔曼滤波算法为基础, 提出了一种抗海浪用实时控制信号滤波方法, 该方法运用状态空间法描述系统, 采用2阶自回归模型计算系统参数, 以递推算法实现计算机实时处理, 从而达到大幅降低信号高频噪声, 抑制陀螺漂移, 提取有用信号的目的。仿真结果表明, 该滤波方法简单, 实现方便, 抑制性好, 可有效减小系统的相位损失, 消除了高频干扰, 对提高系统带宽与系统开环增益有很大贡献。

高频噪声; 实时控制; 扰动

0 引言

陀螺仪是广泛应用于提供惯性空间基准方向的装置。陀螺以及用陀螺构成的稳定平台都具备稳定与跟踪的功能, 这是由陀螺的进动性和定轴性决定的。海上各种平台或浮标中, 一般采用陀螺稳定平台来隔离载体扰动的影响。但是光纤陀螺的稳定性较差, 主要体现在零偏稳定性、零偏温度灵敏度、随机游走等指标中。陀螺的输出噪声和随机游走会直接影响到陀螺稳定平台或浮标伺服系统低速情况下的控制精度和系统的随机漂移。特别当伺服系统在低速输入下工作时, 未经滤波处理的陀螺输出噪声分量的标准偏差值甚至高于陀螺的期望输出值, 使得陀螺输出信噪比显著降低, 期望输出信号淹没于陀螺输出噪声中。伺服系统输出除了跟随输入信号外, 还要跟随陀螺的输出噪声, 控制效果受噪声影响较大, 伺服精度下降。且陀螺自身的漂移包括常值漂移、量化噪声、角度随机游走、零偏不稳定性等影响陀螺稳定平台或浮标的漂移补偿。采用实时补偿的方法可有效去除常值漂移, 但对量化噪声、角度随机游走、零偏不稳定性构成的随机噪声却无能为力。光纤陀螺输出中包含的随机噪声, 常规的漂移补偿方法不能满足系统稳定性要求。上述的2个问题是光纤陀螺应用中必须解决的。传统的滑动平均滤波技术应用可以适当减小陀螺输出噪声, 但效果不理想, 无法很好解决漂移问题。

本文针对光纤陀螺输出噪声大、随机漂移难抑制, 普通滤波算法对陀螺稳定平台伺服系统的控制精度造成的影响, 提出了一种抗海浪扰动光纤陀螺卡尔曼滤波方法, 该方法利用基于2阶自回归模型卡尔曼滤波技术来过滤光纤陀螺的高频噪声抑制系统的随机漂移, 能有效消除陀螺高频噪声, 提高系统的低频性能。

1 算法的主要内容及步骤

该方法优选实施是针对实时控制信号的滤波算法, 通过控制系统中伺服控制软件包实现的, 其中软件包根据图1流程来完成。具体包括: 构建滤波模型; 计算第1步中的矩阵参数; 噪声分析; 建立滤波递推方程; 由建立的递推方程, 对控制信号进行滤波, 将滤波后信号带入系统控制回路等内容。

图1 滤波器建立过程流程图

1.1 构建滤波模型

卡尔曼滤波是用状态空间法描述系统的, 由状态方程(1)和测量方程(2)组成。卡尔曼滤波用前1个状态估计值和最近1个观测数据来估计状态变量的当前值, 并以状态变量估计值的形式给出

1.2 计算第1步矩阵中的参数

采用时间序列法的2阶自回归模型来描述陀螺在系统中的静态输出, 设状态方程为

1.3 噪声分析

1.4 建立滤波递推方程

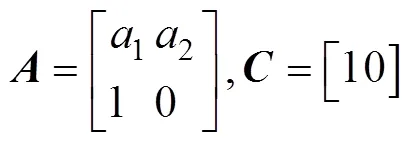
卡尔曼滤波递推公式

图2 建立滤波器递推信号流程图

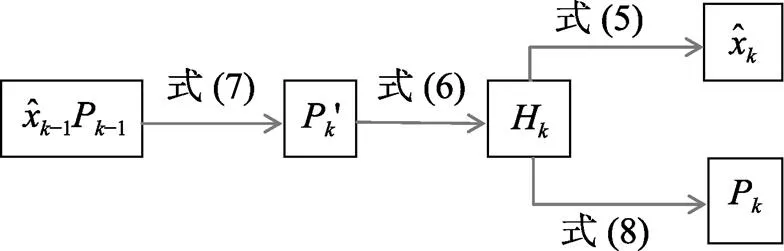
图3滤波方程递推过程图

由建立的递推公式, 对控制信号进行滤波, 将滤波信号带入系统控制回路。

2 仿真结果及分析

以某型光纤陀螺为例, 通过采用上述方法对该型光纤陀螺建立滤波模型, 并使用该模型对此光纤陀螺的静态噪声和叠加噪声分别进行滤波。对静态噪声滤波结果显示, 滤波后方差是滤波前方差的0.335倍; 对叠加随机噪声滤波结果显示, 滤波后方差是滤波前方差的0.201倍。其滤波前后对比如图4、图5所示。

图4 静态噪声波形图

图5 叠加随机噪声波形图

分别采用滑动平均滤波器, 步长设为5步, 数字2阶低通滤波器, 频率为120 Hz以及卡尔曼滤波器, 对光纤陀螺的静态噪声进行滤波, 结果如图6所示(图的中间部分为滤波后波形)。

图6 不同滤波算法结果比较

将上述3种滤波器加入伺服控制系统, 在相同的控制器下, 仿真结果如图7所示。可见, 3种滤波器对系统开环频响曲线的幅值影响区别不大, 但相位影响区别较大。在20 Hz处, 采用卡尔曼滤波器的相位为–104°, 采用滑动滤波器的相位为–123°, 采用2阶低通滤波器的相位为–118°。卡尔曼滤波的相位裕度较大, 还可以继续提高系统开环增益。系统闭环仿真如图8所示, 不同滤波器对系统闭环带宽影响不大。

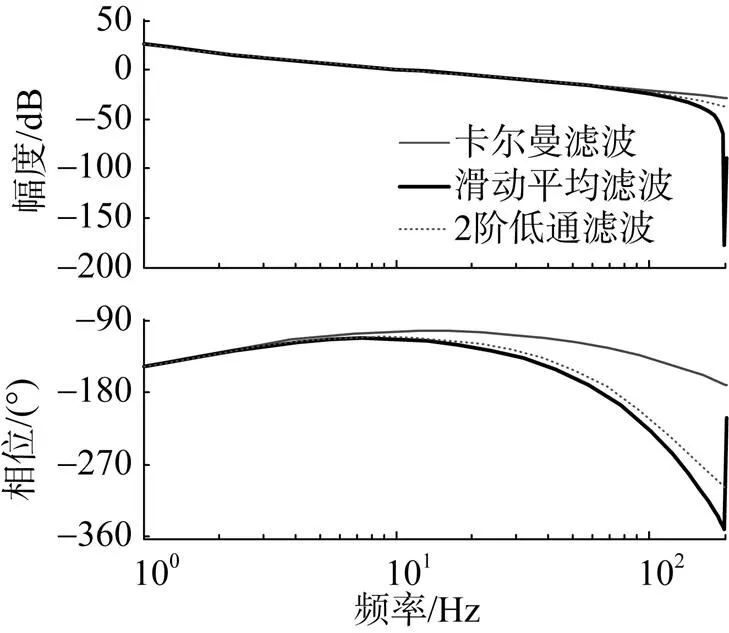
图7 不同滤波器对系统相位的影响

图8不同滤波器对系统闭环曲线的影响

3 结束语

综上所述, 本算法的预期效果体现在以下几个方面: 通过对光纤陀螺建立滤波模型, 针对噪声特性进行滤波, 使得本算法能消除高频干扰, 有效抑制漂移; 该方法以卡尔曼滤波为基础, 由2阶自回归模型计算滤波参数, 相比于其他滤波方法, 减小了系统的相位损失, 可以提高系统开环增益, 有利于提高控制系统的动态性能; 该方法中的滤波算法简单, 实现方便, 移植性好, 具有广阔的应用前景。

[1] 邓自立. 卡尔曼滤波与维纳滤波[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001.

[2] 郑大钟. 线性系统理论[M]. 北京: 清华大学出版社, 2002.

[3] Anderson B D O, Moore J B. Optimal Filtering[M]. New York: Prentice Hall, Englewood Cliffs, 1979.

[4] Kalman R E. A New Approach to Linear Filtering and Prediction Problem[J]. Transactions of the ASME, Journal of Basic Engineering, 1960, 84(5): 35-45.

(责任编辑: 杨力军)

A Filtering Method of Anti-waves Disturbance Real-time Control Signal

Zhao JiangXiao chang-meiLei fei-linJiang taoWang chao

(Naval Academy of Armament, Beijing 100161, China)

To solve the problem that filtering effect is incompatible with phase margin in servo control system, while eliminating high-frequency noise will lose useful low-frequency signal, we present a filtering method of anti-waves disturbance real-time control signal based on Kalman filter algorithm. In this method the system is described by state space method, the second-order autoregression model is used to calculate the system parameters, and recursive algorithm is adopted to achieve real-time process of computer, thus the high-frequency noise can be significantly removed, the gyro drift can be suppressed and the useful signal can be extracted. Simulation result shows that this method is simple and convenient in implementation, and has good disturbance suppression performance. Moreover, it effectively reduces the loss of system phase, eliminates the high-frequency interference, and greatly contribute improvement to the system bandwidth and the open loop gain.

high-frequency noise; real-time control; disturbance

TJ630.34; TB53

A

1673-1948(2014)01-0035-04

2013-05-07;

2013-09-18.

赵 江(1979-), 硕士, 工程师, 主要研究方向为武器系统与运用工程.