基于变结构控制的反鱼雷鱼雷导引律鲁棒性研究
李宗吉, 张西勇, 练永庆
基于变结构控制的反鱼雷鱼雷导引律鲁棒性研究
李宗吉, 张西勇, 练永庆
(海军工程大学 兵器工程系, 湖北 武汉, 430033)
为了解决水下目标信息参数测量数据率低带来的制导困难问题, 设计了基于变结构控制的反鱼雷鱼雷(ATT)导引律, 导引律中取变结构控制器使得ATT与来袭鱼雷间视线角保持恒定, 且控制器对模型参数摄动具有强鲁棒性。理论分析表明, 模型参数摄动不影响导引律的稳定性, ATT和目标间视线角能够保持恒定。仿真结果验证了该导引律对模型参数摄动具有强鲁棒性, ATT能够精确命中目标。
反鱼雷鱼雷; 导引律; 变结构; 鲁棒性
0 引言
传统鱼雷导引律主要有追踪法、提前角法等, 这些导引律在鱼雷攻击大型水面舰艇和潜艇等大目标时其命中精度在一定条件下能够满足要求, 但对付小目标比如鱼雷时, 由于制导精度差, 很难对目标造成杀伤[1-2]。在设计基于变结构控制的反鱼雷鱼雷(anti-torpedo torpedo,ATT)导引律的基础上, 对导引律的鲁棒性进行了研究。由于目标信息参数测量中存在误差, 比如ATT和目标的距离以及距离的导数, 这些参数在测量和估计时不可能完全准确, 误差可能会对导引律的命中精度产生影响。文献[1]研究了变结构ATT导引律, 从推导过程看导引律的稳定性结论并不成立, 对其鲁棒性也没有进行分析。本文在设计基于变结构控制的ATT导引律的基础上就模型参数测量误差对导引律的稳定性影响进行了理论分析, 并进行了仿真验证。
1 ATT导引律
以平面内情况为例, ATT-来袭鱼雷相对运动关系如图1 所示。

图1 平面内ATT-来袭鱼雷相对运动关系
由图1可导出



令
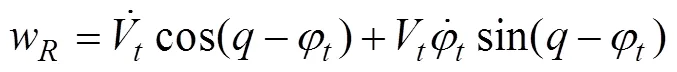
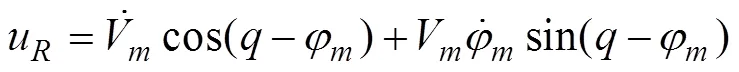


将式(4)~式(7)代入式(2)和式(3), 并考虑式(1), 得
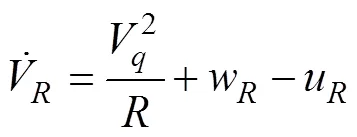
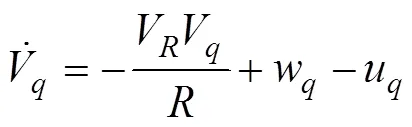

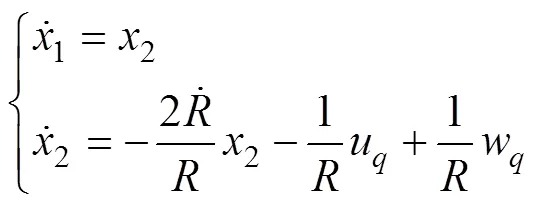
基于准平行接近原理, 选取切换平面为[3-4]

根据式(11) , 构造滑模趋近律

将式(12)和式(11)代入式(13), 得滑模制导律

2 导引律的鲁棒性分析


把式(14)代入式(16), 得
3 仿真结果与分析
仿真模型如下

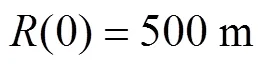
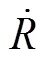

从仿真结果可以看出, 参数测量误差不影响ATT与目标视线角保持恒定, 对ATT和目标弹道影响甚小。ATT和目标弹道是通过解算式(18)得到的ATT和目标航向角绘制ATT和目标运动轨迹而得到的, 从仿真结果可以看出, ATT精确命中目标, 命中点处细化图存在的误差是由于仿真存在截断误差造成的。仿真结果与前面理论推导的结论一致。
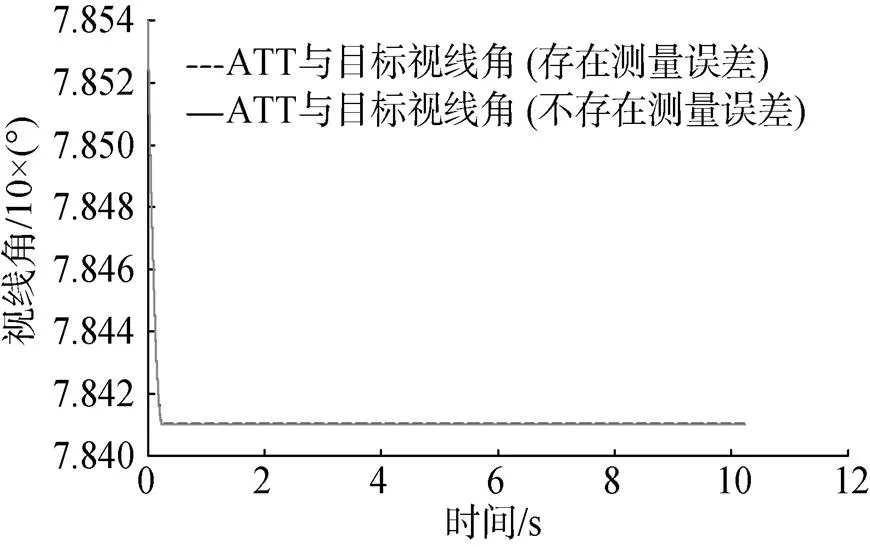
图2 目标不作机动时ATT与目标视线角随时间变化曲线

图3 目标不作机动时ATT 与目标视线角速度随时间变化曲线

图4 目标不作机动时ATT航向角随时间变化曲线
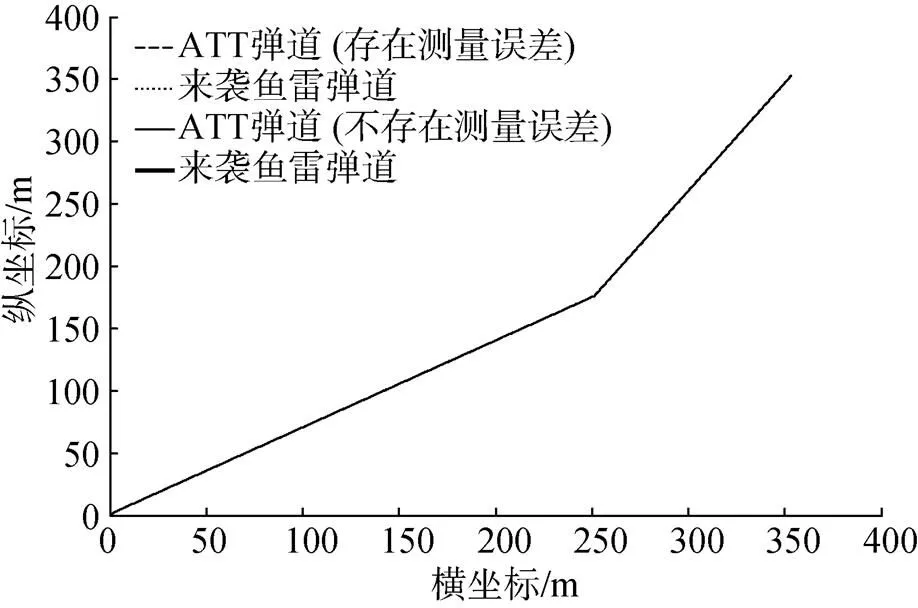
图5 目标不作机动时ATT和目标弹道曲线
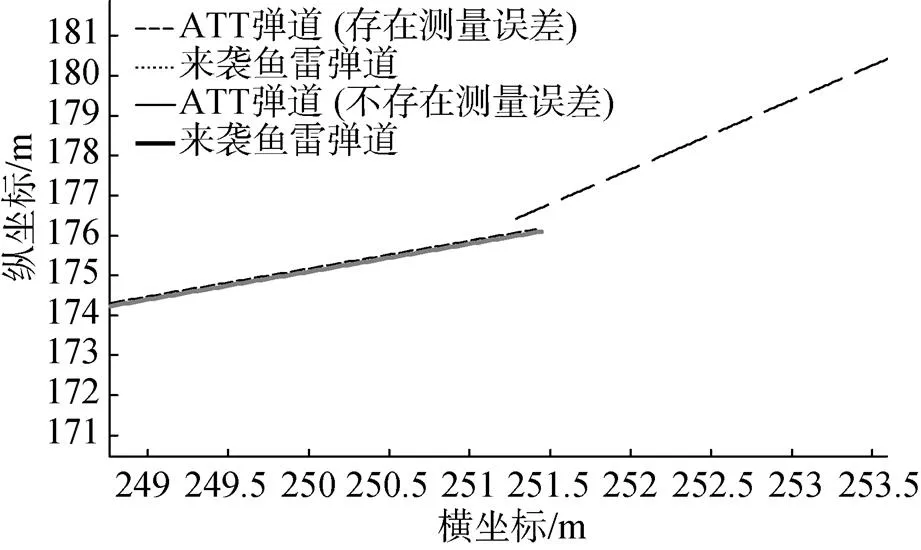
图6 目标不作机动时命中点处弹道细化图
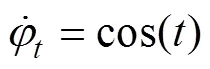
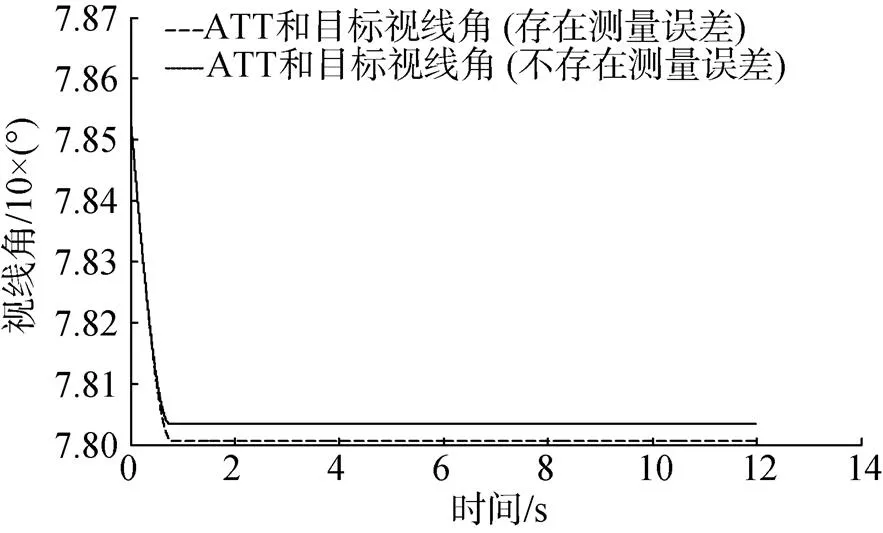
图7 目标蛇形机动时ATT与目标视线角随时间变化曲线
从仿真结果可以看出, 当目标机动时, 参数测量误差不影响ATT与目标视线角保持恒定, 从图8可以看出, 测量误差对视线角速度存在干扰,但不影响视线角保持恒定, 从图10可以看出, 测量误差对ATT和目标弹道影响很小, 验证了前面的理论推导。

图8 目标蛇形机动时ATT和目标视线角速度随时间变化曲线

图9 目标蛇形机动时ATT航向角随时间变化曲线
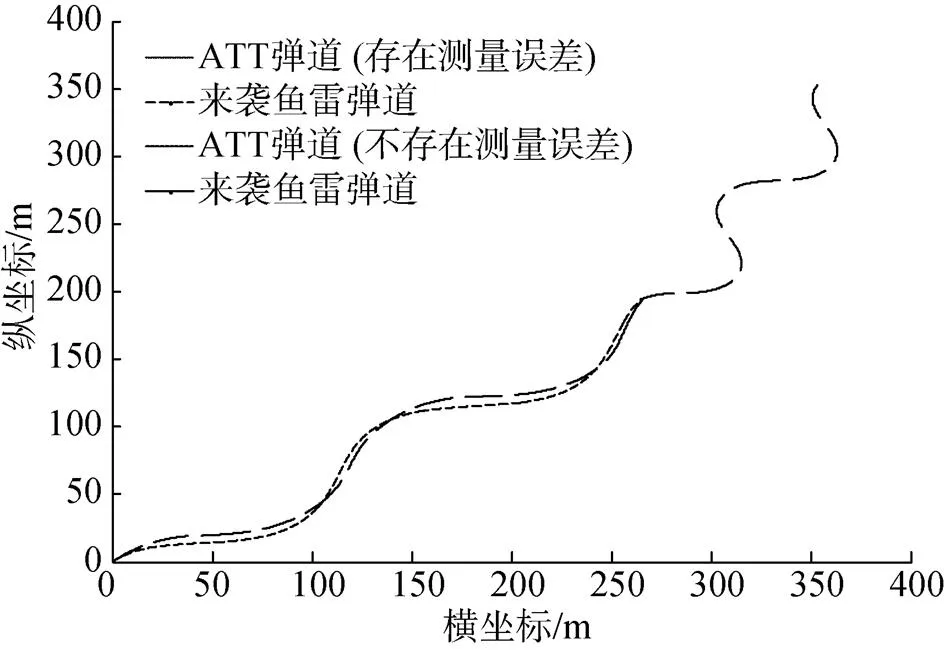
图10 目标蛇形机动时ATT和目标弹道

图11 目标蛇形机动时命中点处弹道细化图
4 结束语
在设计反鱼雷鱼雷导引律的基础上, 针对导引律对参数误差的鲁棒性进行了研究, 通过理论推导证明, 导引律对参数摄动具有鲁棒性, 即导引律模型参数一定范围的测量误差不会对导引律的稳定性产生影响。仿真结果表明, 导引律对模型参数的摄动具有强鲁棒性, ATT在导引律的作用下准确命中目标。该研究成果对反鱼雷鱼雷在目标方位信息测量存在误差时也能够精确命中目标具有较大的参考价值。
[1] 刘宇. 基于变结构控制的反鱼雷武器导引律[J]. 火力与指挥控制, 2010, 35(10): 87-90.
Liu Yu. Anti-torpedo Weapon Guidance Law Based on Control, 2010, 35(10): 87-90.
[2] 丁浩, 由文立, 藤达. 一种新型鱼雷非线性变结构导引律设计[J]. 鱼雷技术, 2011, 19(1): 35-38. Ding Hao, You Wen-li, Teng Da. A New Nonlinear Vari- able Structure Guidance Law for Torpedo[J]. Torpedo Te- chnology, 2011, 19(1): 35-38.
[3] 王湛, 贾晓洪, 阎杰. 空空弹道末端控制滑模导引律研究[J]. 航空兵器, 2005(2): 3-6.
Wang Zhan, Jia Xiao-hong, Yan Jie. Study on the End Ga- me Sliding-Mode Guidance Law of Air-to-air Missile[J]. Aero Weaponry, 2005(2): 3-6.
[4] 高为炳.变结构控制理论基础[M]. 北京: 中国科学技术出版社, 1990.
[5] 高磊, 徐德民, 任章.被动式鱼雷的自适应变结构制导律设计[J]. 兵工学报, 2001, 22(2): 280-283.Gao Lei, Xu De-min, Ren Zhang. Adaptive Variable Stru- cture Guidance Law For Passive Torpedo[J]. Acta Armamentarii, 2001, 22(2): 280-283.
[6] 孙胜, 周狄. 离散滑模导引律设计[J]. 航空学报, 2008, 29(6): 1634-1639.
Sun Sheng, Zhou Di. Desing of Discrete Sliding-mode Guidance Laws[J]. Acta Aeronautica ET Astronautica Sinica, 2008, 29(6): 1634-1639.
[7] Wang Yu-hang. Lateral Thrust and Aerodynamics Blended Control System Design Based on Variable Structure Model Following[C]//Proceedings of 6th World Congress on Intelligent Control and Automation.China: IEEE, 2006: 8183-8186.
(责任编辑: 杨力军)
Robustness of Anti-Torpedo Torpedo Guidance Law Based on Variable Structure Control
LI Zong-jiZHANG Xi-yongLIAN Yong-qing
(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)
For solving the difficulty in the guidance of anti-torpedo torpedo(ATT) due to low data ratio of underwater target information detection, an ATT guidance law based on variable structure control is designed, in which a variable structure controller is employed to keep a constant line-of-sight angle between ATT and incoming torpedo, and the controller shows good robustness for perturbation of model parameters. Theoretical analysis shows that perturbation of model parameters has no effect on the stability of the guidance law, and the line-of-sight angle between ATT and target can keep constant. Simulation validates that the proposed guidance law has good robustness for perturbation of model parameters, and the ATT with the guidance can hit target precisely.
anti-torpedo torpedo; guidance law; variable structure; robustness
2014-04-22;
2014-05-28.
船舶工业国防科技预研基金项目(401060901-0261-002).
李宗吉(1974-), 男, 副教授, 主要研究方向为水中兵器制导与控制技术.
TJ630.33
A
1673-1948(2014)04-0272-05

