汽车钢板弹簧多体动力学建模综述*

古玉锋，吕彭民，单增海

(1.长安大学，道路施工技术与装备教育部重点实验室，西安 710064；2.徐工集团徐州重型机械有限公司，徐州 221004)

前言

钢板弹簧目前乃至以后相当长的时间仍将是载货车辆悬架系统使用的主要弹性元件[1]之一，其设计方法也一直是国内外同行研究的热点问题。2004年以来，国内各大企业为了适应国家标准[2]的要求，不断推出了多轴的重型车辆[3]，随着车轴数的增加，对于悬架系统的研究已不仅局限于1/4车辆模型[4]，以整车模型研究为目标已是当今国际汽车设计方法领域的主流[5]，悬架系统模型在整车模型中扮演着关键的角色[6]，板簧模型相比于其它形式的悬架弹性元件模型而言，更加复杂，模型的复杂程度直接与仿真精度、速度和出错的概率相关。因此，“精确、高速、可靠”的板簧模型的建立是整车模型建立的关键。本文中将在综述国内外板簧设计方法现状的基础上，对目前国际上流行的几种板簧建模方法进行详细分析，以便为设计提供参考。

1 钢板弹簧建模和设计的国内外研究现状

1.1 国内研究现状

国内各企业对于车用钢板弹簧的设计多年来一直依据文献[7]中所提出的共同曲率法和集中载荷法。文献[8]中研究了主片分析法。文献[9]中假定第i片板簧由3部分组成,对文献[8]进行了改进。但文献[8]和文献[9]只适合于以编程的方式进行板簧的优化设计，而不适合于板簧的多体动力学建模。

文献[10]中采用Timoshenko梁建立了板簧的多体动力学模型，该模型是依据小变形理论，将板簧等效成一定数量的微小梁连接起来的刚体组合，模型包含的构件数多，仿真速度慢，且不易参数化。文献[11]中利用Nastran软件的非线性模块，建立了多片钢板弹簧的有限元模型，该模型经过模态分析后即可导入ADAMS软件中进行仿真，但模型不能参数化，且使用不便。文献[12]中应用ANSYS软件中的APDL语言建立了少片簧的参数化有限元模型，但该模型只针对少片钢板弹簧，使用APDL语言建立多片簧参数化模型由于计算量大而很少使用。

1.2 国外研究现状

文献[13]和文献[14]中基于有限元浮点坐标法，使用相对于板簧参考坐标系的节点自由度模拟板簧的几何模型和变形，建立了一种多体动力学仿真的钢板弹簧非线性模型，该模型简单，自由度少，适合进行整车的仿真，但模型无法参数化，且不能进行板簧的优化设计。文献[15]中在考虑片间接触的情况下，以确定板簧的变形图为目标分析了板簧的受力与变形之间的关系，但该模型也无法参数化。文献[16]中为了模拟板簧的柔性，将板簧离散化成若干段刚性杆(rigid link)通过弹簧和阻尼连接起来的模型，该模型类似于ADAMS中的beam梁模型，杆的数量和自由度多，仿真速度慢。文献[17]中建立了多片板簧的有限元模型，考虑了片间接触和摩擦，精度较高，但为了提高模型精度，有限元模型节点数较多，模型复杂，自由度多，不适合进行整车的多体动力学仿真和板簧的优化设计。

已有文献说明：对于板簧的优化设计，目前主要采用集中载荷法和共同曲率法及其改进型模型[18]，少片簧有采用ANSYS软件中APDL语言进行参数化优化设计的[10-12]，但在基于ANSYS的多片簧优化设计中，APDL语言很少使用，板簧的该类优化设计模型不适合板簧的多体动力学仿真；在CAE分析方面主要采用有限元法，该模型适合于对已有板簧进行分析，参数化困难，也不适合多体动力学仿真。目前适合于多体动力学仿真的多片簧模型主要有4种：一是采用力元或螺旋弹簧元件[19]，二是采用ADAMS/Chassis模块中的beam element Leaf Springs Model[20]，三是采用有限元模型[10-12]，四是采用ADAMS/Chassis模块中的SAE 3-Link Leaf Springs Model[21]。

2 目前几种流行的板簧建模方法分析

以某8×4重型货车悬架钢板弹簧(见图1)为例，分析第1.2节所述的4种板簧建模方法。

2.1 力元或螺旋弹簧元件等效代替的板簧模型

在分析汽车的振动频率特性或平顺性研究中，重点关注其垂向振动特性，因此用力元或螺旋弹簧等效代替板簧，可简化整车模型，并具有一定的精度。图2为板簧弹性元件使用螺旋弹簧代替的整车多体动力学模型(驾驶室和货箱在软件中隐藏，图中未示出)，转向轴悬架导向杆与转向轴和车架、平衡悬架导向杆与驱动桥和车架分别通过转动副连接。

该类模型的优点是：①能准确反映单个板簧的垂向刚度特性，在刚度对话框中可以输入板簧的刚度值或根据试验曲线拟合的弹簧力与位移的函数关系式，即板簧刚度函数，在阻尼对话框中同样可输入阻尼值或根据试验拟合的阻尼函数；②模型简单，仿真速度快；③易于参数化。缺点是：由于螺旋弹簧无导向作用，此模型不能准确描述车轴与车架的相对运动关系，在一、二转向轴与车架之间还必须使用导向杆连接，整车仿真中左右车轮将同时上下跳动。

力元或螺旋弹簧元件等效代替的板簧模型常用于ADAMS/Vibration中分析悬架的振动特性，也常用于整车的平顺性仿真。

2.2 ADAMS/Chassis模块中的梁单元板簧模型

依据小变形理论，可将板簧等效为一组用p片且每片又分成q段的板簧，段与段之间采用beam力约束，此即为板簧的梁单元(beam element)模型。图3为板簧弹性元件使用梁单元板簧模型(beam element leaf springs model)代替的整车多体动力学模型，模型依据实车结构建立。图4和图5分别为转向轴板簧和驱动桥平衡悬架板簧的梁单元模型(图中显示了力元和运动副)，而实际建模时一般是在ADAMS/Chassis中通过Leaf Spring Preprocessor参数输入界面进行建模，然后导入ADAMS其它模块中进行相应的仿真。

该类模型的优点是：①模型能较精确地反映钢板弹簧工作的实际情况，包括板簧的垂向刚度特性及车轴与车架的相对运动关系；②建模过程简单，只须通过Leaf Spring Preprocessor参数输入界面输入板簧的几何参数，即可通过软件生成新的模型。缺点是：①模型的精度与所建模型中板簧的片数和每片所分的段数有关，板簧片数越多、分段数越多则精度越高，但每片究竟取多少段最为合适，ADAMS/Chassis中并未给出推荐值；②模型中含有相当数量的beam约束力(见图4和图5)，其复杂程度显而易见，模型无法参数化；③ADAMS/Chassis中所能建的板簧的梁单元模型的片数有限制，最多为10片；④卷耳的形状只有3种，即上卷耳、下卷耳、平卷耳，如图6所示，若要建立平衡悬架板簧模型，须将图4中的卷耳删除，这样必将再次引入误差。

ADAMS/Chassis模块中的梁单元板簧模型常用于轻型车辆的整车仿真，不适合进行多轴、有平衡悬架的重型车辆的整车仿真。

2.3 有限元模型

板簧的ANSYS模型依据大变形动力学基本方程建立。实际建模时，依据板簧前后不对称的特点，在前后卷耳处施加不同的约束，片与片之间采用动摩擦处理，摩擦因数为0.2，采用面面接触单元模拟钢板弹簧各片间的接触，以8节点三维实体单元SOLID185划分单元网格。本文所建转向轴悬架板簧ANSYS模型如图7所示，进一步利用ANSYS软件生成ADAMS软件所需要的模态中性文件(.mnf文件)，而后导入ADAMS软件中建立整车模型，该方法所建整车模型与图3类似，这里不再详述。

该类模型的优点是：模型能精确地反映钢板弹簧工作的实际情况，包括与车架和车轴的相对运动关系及板簧的强度和刚度等，并建立了板簧的几何参数、变形与应力之间的关系。缺点是：①须已知板簧的材料特性，且建模和求解过程复杂；②模型网格单元数量庞大，模型无法参数化，仿真速度慢。

基于ANSYS的板簧模型常用于板簧的应力、疲劳分析，也常用于板簧的刚度试验验证。在轻型车辆的整车仿真方面也常使用，但一般不用于多轴、平衡悬架重型车辆的整车仿真。

2.4 ADAMS/Chassis模块中的SAE三连杆板簧模型

由于板簧的中段通过U形螺栓与车桥联接，使用中该段板簧不参与板簧的变形，据此可以将板簧分为3段，即板簧的SAE三连杆模型。

图8和图9分别为转向轴板簧和驱动桥平衡悬架板簧的SAE三连杆模型，“三段梁”的前段与中段之间、中段与后段之间同时通过Spherical和Bushing连接。

各段长度由首片长度确定，如图10和图11所示，L为首片板簧弧长，m、n分别为前后U型螺栓与板簧中心的距离，a、b分别为板簧前后半段弧长，c为板簧后吊耳长度，Ra、Rc和Rb分别为板簧三连杆模型的前段、中段和后段长度，d为板簧中段前端与车桥轴线的距离，且

(1)

刚度特性通过Modify Bushing对话框中对Bushing的参数设计来实现，将Translational Properties参数全部设置为零，将Rotational Properties中的Damping参数设置为零，设KTX、KTY和KTZ分别为Stiffness中沿3个坐标轴的旋转刚度，其中KTX、KTY通过对有限元模型的测试获得，KTZ由式(2)计算，设TOX、TOY和TOZ分别表示Preload中板簧纵向、横向和垂向的预加载荷，其中TOX和TOY设置为零，板簧的满载弧高由TOZ确定，其值由式(3)计算。

(2)

(3)

式中：sls为板簧垂向刚度；fah为板簧自由弧高。

该类模型的优点是：①与梁单元模型相同，能较精确地反映钢板弹簧工作的实际情况；②建模过程简单，只须输入Modify Bushing对话框中的Bushing参数即可确定板簧的刚度特性；③该方法需要的参数少，构件少，容易实现整车的参数化，仿真速度快；④将板簧的刚度特性与Bushing参数联系起来可以对板簧进行优化；⑤与梁单元模型相比，可根据实际情况建立平衡悬架模型。缺点是：①SAE三连杆板簧模型为一近似模型，ADAMS/Chassis中只给出各段长度的计算式(见式(1))，并未做过多说明；②Bushing参数如果给的不准确也会引入刚度误差，其值的确定还须进一步的研究。

SAE三连杆板簧模型常用于复杂的整车仿真中，包括平顺性仿真和操纵稳定性仿真。

采用SAE三连杆板簧模型的整车模型如图12所示。模型共有129个参数，且已全部参数化，其中转向传动机构24个参数，转向操纵机构5个参数，各转向节转向梯形机构12个参数，横向稳定杆8个参数，悬架系统18个参数，车轮/车轴32个参数，车身部分30个参数。由此可见，板簧模型的简化使得整车的参数化模型大为简化。

3 整车模型的仿真与实车试验

现对包含第2章节所建的4种板簧模型的整车(整备质量31t)模型进行平顺性与操纵稳定性仿真分析，并与实车试验结果进行对比。

3.1 实车试验准备

实车试验在长安大学汽车试验场进行。平顺性试验货厢质心垂向振动加速度传感器安装在距离车厢前端挡板4m，离地高度1.3m的车厢副梁上，如图13所示，试验按照GB/T 4970—2009进行；操纵稳定性试验及其安全支架如图14所示；埋于货厢质心处的6自由度陀螺仪(见图15)用于测量货厢质心3个坐标轴的加速度和绕3个坐标轴的旋转角度与角速度；此外，使用上海好耐电子有限公司的HR-GPS-20型GPS测量车速；淄博科创电子有限公司的ZL-1L型转向盘参数测试仪测量转向盘的转角和转矩，试验按照GB/T 6323.3—1994进行。所有数据由HORIZON数据采集仪采集并存储。

3.2 平顺性仿真与试验

ADAMS仿真中，通过对话框直接输入螺旋弹簧刚度值；梁单元模型和有限元模型依据Pro/E模型建立；SAE三连杆模型参数依据设计值间接设定。

设定仿真时间为50s，步数为1 000，车速为40km/h，汽车在B级路面上直线行驶，对货厢质心垂向加速度进行测量并进行FFT变换，仿真结果如图16～图19所示，图20为实车试验结果，将试验测得的数据导入ADAMS中即可得到。

3.3 操纵稳定性仿真与试验

设定仿真时间为50s，步数为1 000，车速为28km/h，转向盘转角为665°(左转)，进行转向盘阶跃输入仿真，图21为横摆角速度的仿真与测试结果，其均值在ADAMS后处理中直接得到。

3.4 最小转弯半径仿真与试验

设定仿真时间为50s，步数为1 000，汽车以接近最低稳定车速5.3km/h行驶，转向盘输入转角为右转时的最大转角820°(试验与仿真均已证实右转极限位置时，该车转弯半径最小)。图22为最小转弯半径仿真与测试结果，其均值同样在ADAMS后处理中直接得到。

3.5 仿真与试验结果分析

表1为各模型的测量结果，表2为模型信息和仿真结果对比。

表1 各模型的测量结果

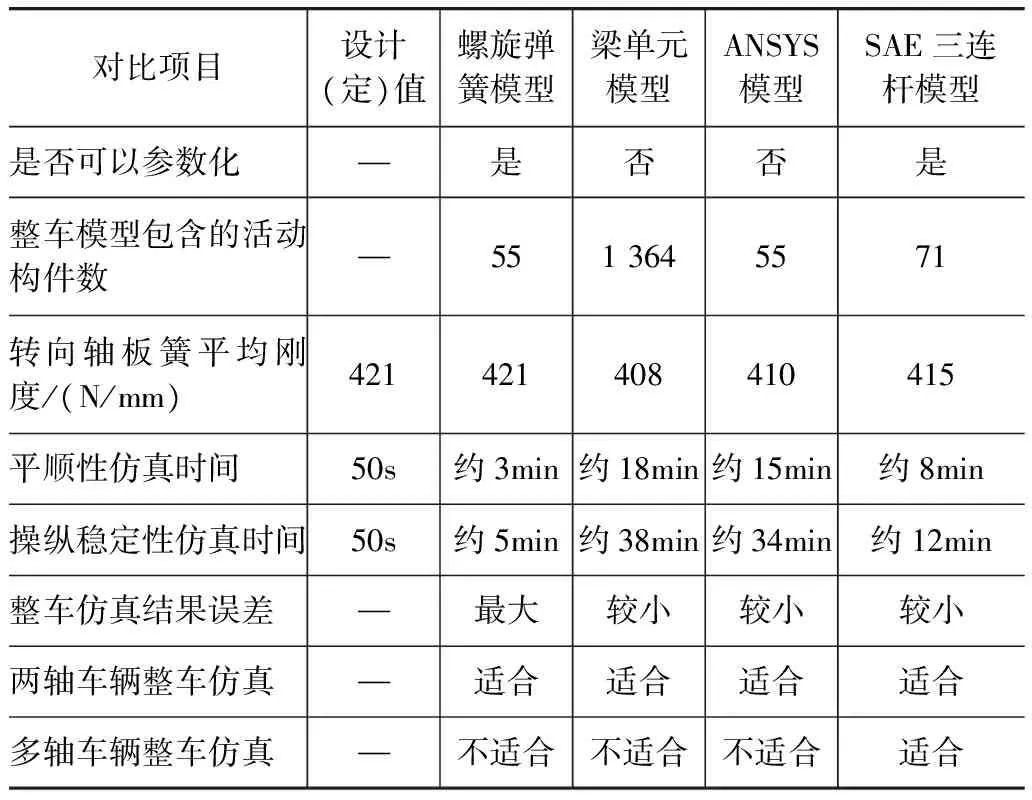
表2 各模型的信息与仿真结果

(1) 由表1可知，螺旋弹簧板簧模型由于不能正确反映车轴与车架的正确运动关系，货厢垂向振动主频率、转向盘阶跃输入时横摆角速度均值和最小转弯半径的误差均最大，梁单元板簧模型与ANSYS板簧模型的误差均较小，SAE三连杆板簧模型的误差居中。

(2) 由表2可知，仿真速度方面，相对于仿真设置的50s，螺旋弹簧板簧模型的整车平顺性和操纵稳定性仿真分别需要3min和5min，SAE三连杆板簧模型的整车仿真分别需要8min和12min，梁单元板簧模型与ANSYS板簧模型由于计算量大，仿真时间最长。模型的复杂程度方面，梁单元模型的整车包含的构件数庞大，其它3种板簧模型的整车包含的构件数均较少，模型较简单。模型的参数化方面，仅有螺旋弹簧和SAE三连杆板簧模型的整车可以参数化。

综上所述，4种板簧模型中，SAE三连杆板簧模型在整车建模和仿真方面均具有较好的适用性。

4 结论

(1) 集中载荷法、共同曲率法及其改进型方法仍是目前板簧优化设计(以板簧的几何参数为目标)的主流方法，ANSYS中的APDL语言适用于少片簧的设计，多片簧很少使用。但这几种板簧的优化模型都不能用于板簧的多体动力学仿真。

(2) 在整车层面上，若要对板簧系统刚度与阻尼进行优化，首先必须参数化整车模型，从这个角度考虑，螺旋弹簧的板簧模型和SAE三连杆板簧模型更有优势，但是螺旋弹簧的板簧模型精度最低，与螺旋弹簧模型、梁单元模型和有限元模型相比，SAE三连杆板簧模型在板簧精度和仿真速度两方面之间进行了折中，适合复杂多轴车辆的整车仿真。

(3) SAE三连杆板簧模型误差较小，仿真速度快，未来可以通过参数辨识或试验的方法精确地确定其参数。

(4) 正确确定有限元模型中的板簧各片间的接触状态、摩擦因数和输出模态中性文件的阶数将是未来一段时间板簧有限元模型的研究重点。

(5) 采用有限元浮点坐标法，基于板簧的几何模型、变形曲线与协调关系，建立适用于多体动力学仿真的板簧非线性模型也将是未来的板簧多体动力学模型的发展方向，该种模型将有限元理论与多体动力学仿真联系起来，具有一定的潜力。

[1] Singh Jagjit,Singh S Paul,Joneson Eric.Measurement and Analysis of US Truck Vibration for Leaf Spring and Air Ride Suspensions,and Development of Tests to Simulate these Conditions[J].Packaging Technology and Science,2006,19(6):309-323.

[2] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化委员会.GB 1589—2004 道路车辆外廓尺寸、轴荷及质量限值[S].2004.

[3] 古玉锋,方宗德,张国胜.重型车辆多轴转向系统设计综述[J].汽车技术,2009(1):1-6.

[4] Hac A,Youn I.Optimal Design of Active and Semi-Active Suspensions Including Time Delays and Preview[J].Trans ASME,Journal of Vibration and Acoustics,1993,115:498-508.

[5] Michael Blundell,Damian Harty.The Multibody Systems Approach to Vehicle Dynamics[M].Amsterdam: Elsevier,2004.

[6] 汽车工程手册编辑委员会.汽车工程手册设计篇[M].北京:人民交通出版社,2001.

[7] 帕尔希洛夫斯基И Г.汽车的钢板弹簧[M].宁开平,译.北京:人民交通出版社,1959.

[8] 郭孔辉.钢板弹簧刚度计算的主片分析法[J].汽车工程,1984,6(2):22-28.

[9] 张立军,何辉,郁工瑞.钢板弹簧新的计算方法及其在设计中的应用[J].汽车工程,1994,16(1):50-57.

[10] 王其东,方锡邦,钱立军.基于虚拟样机技术的汽车钢板弹簧设计及分析研究[J].机械工程学报,2001,37(12):63-66.

[11] 于安和,桂良进,范子杰.钢板弹簧刚度特性的有限元分析[J].汽车技术,2007(2):26-30.

[12] 李东月.基于APDL的车辆钢板弹簧参数化设计与优化[D].西安:西北工业大学,2010.

[13] Hiroyuki Sugiyama,Ahmed A Shabana,Mohamed A Omar,et al.Development of Nonlinear Elastic Leaf Spring Model for Multibody Vehicle Systems[J].Computer Methods in Applied Mechanics and Engineering,2006,195:6925-6941.

[14] Mohamed A Omar.Finite Element Modeling of Leaf Springs for Vehicle System Applications[D].Chicago: University of Illinois at Chicago,2003.

[15] Osipenko M A,Nyashin Yu I,Rudakov R N.A Contact Problem in the Theory of Leaf Spring Bending[J].International Journal of Solids and Structures,2003,40:3129-3136.

[16] Rill G,Kessing N,Lange O,et al.Leaf Spring Modelling for Real Time Applications[C].Proceedings of International Association of Vehicle System Dynamics (IAVSD) 18th Symposium,Atsugi,Japan,2003:1-7.

[17] Li Q,Li W.A Contact Finite Element Algorithm for the Multileaf Spring of Vehicle Suspension Systems[J].IMEC-E Part D: J.Autom.Engrg,2004,218:305-314.

[18] 刘惟信.汽车设计[M].北京:清华大学出版社,2001.

[19] 戚玉轩.载重汽车平顺性研究与悬架参数优化[D].西安:西北工业大学,2010.

[20] Uday Prasade,Sudhakar Medepalli,Daniel Moore,et al.Beam Element Leaf Spring Suspension Model Development and Assessment Using Road Load Data[C].SAE Paper 2006-01-0994.

[21] Jayakumar P,Alanoly J,Johnson R.Three-Link Leaf-Spring Model for Road Loads[C].SAE Paper 2005-01-0625.