转向系间隙对汽车操纵稳定性影响研究*
魏道高,王子涵,张翼天,肖怀阳
(合肥工业大学机械与汽车工程学院,合肥 230009)
前言
汽车操纵稳定性是转向动力学性能中最主要的性能之一,是高速车辆的生命线。自20世纪30年代人们就开始进行汽车操纵稳定性的研究,目前其线性范围研究较为成熟[1-3],而非线性范围研究较为滞后,与线性范围相比,其转向稳定性相图有多个平衡点,能较全面地反映车辆转向行驶的本质特性,避免了线性系统只取某一平衡点的邻域构建线性模型,用来描述车辆行驶动特性的局限性[4-5]。
然而,汽车是多自由度的非线性系统,随着其设计与实际行驶速度的提高,车辆转向行驶的非线性动力学行为变得更加明显,在工程实际中,显现出来的一系列问题也更加突出。对其问题国内外学者展开了深入的研究,取得了一系列成果,并且为车辆转向行驶非线性动力学的控制奠定了理论基础。例如,文献[6]中建立了前轮转向的2自由度汽车转向行驶非线性系统动力学模型,运用分岔理论对其动力学行为进行数值分析,提出了随着车辆行驶速度和前轮转向角的增加系统发生鞍-结分岔;文献[7]中建立了四轮转向的2自由度汽车转向行驶非线性系统模型,运用共点轨迹的几何分析法并结合相平面法对汽车转向行驶稳定性进行了数值分析,提出在极限工况下,系统除了发生鞍-结分岔,还会发生多种局部、全局分岔和极限环;文献[8]中考虑车辆纵向速度的变化,建立了3自由度的汽车转向行驶非线性系统动力学模型,对其进行数值分析,发现系统出现混沌运动。但是,以上学者的研究局限于轮胎非线性对转向行驶稳定性影响,而转向系统的间隙因素对汽车转向行驶稳定性的非线性动力学影响的研究未见报导。
在以上学者研究的基础上,本文中考虑转向系间隙非线性因素,建立了含车身侧倾运动的4自由度汽车转向行驶非线性动力学模型,对该系统进行数值计算与分析,以获得间隙因素对汽车转向行驶系统操纵稳定性的影响,进一步丰富汽车转向行驶系统非线性力学理论。
1 考虑转向系间隙的操纵稳定性动力学模型
1.1 考虑间隙的操纵稳定性系统力学模型
在前人建立的汽车操纵稳定性力学模型的基础上,本文中考虑转向系间隙对操纵稳定性的影响,建立了车辆操纵稳定性力学模型和坐标系,如图1所示[9-10]。由于考虑转向系间隙,忽略前轮定位参数影响,将汽车的转向梯形机构看作平面四连杆机构,如图2所示。为简化分析过程,仅考虑主动梯形臂(左)和横拉杆连接处有间隙,杆件均看作刚体。汽车以速度v进行等速转向行驶,oxyz为固定于侧倾中心的坐标系,xoy与路面平行,x轴指向汽车行驶方向,z轴垂直向上,y轴按右手定则指向左侧。
操纵稳定性系统力学模型作如下假设:
(1)不计空气阻力;(2)前后悬架侧倾中心相同;(3)忽略前轮定位参数影响,转向梯形机构与xoy坐标平面平行。
汽车操纵稳定系统用4个自由度表示:横摆角速度ω、质心侧偏角β、车身侧倾角φ和前轮转角δ。
1.2 考虑间隙的操纵稳定性系统运动微分方程
根据以上图1、图2力学模型,运用达朗贝尔定理,建立系统运动微分方程。
1.2.1 操纵运动系统微分方程
(1)整车系统绕z轴的力矩平衡方程式
(1)
式中:Iz为绕z轴惯性矩;Ixz为惯性积;a、b分别为质心到前后轴距离;Fy1、Fy2分别为前后轮侧向力。
(2)整车系统沿y轴力平衡方程式
Fy1-Fy2=0
(2)
式中:M为整车质量;Ms为悬架上质量;h为车身质心到整车侧倾中心距离;v为汽车行驶速度。
(3)车身绕x轴侧倾力矩平衡方程式
(3)
式中:Df、Dr分别为前后悬架侧倾阻力系数;Cφ1、Cφ2为前后悬架侧倾角刚度;Ix为绕x轴惯性矩。
(4)前主动转向轮(左)绕主销力矩平衡方程式
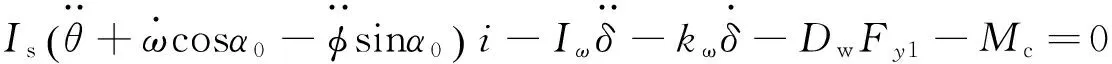
(4)
式中:T为转向盘转入力矩;i为转向系传动比;Is为转向盘转动惯量;Iω为前轮绕主销转动惯量;Dw为回正力臂;Mc为转向梯形间隙碰撞力矩;kω为转向系阻尼系数;α0为转向柱与z轴夹角;θ为图2所示转向梯形中对应夹角。
1.2.2 汽车轮胎侧向力表达式
汽车轮胎侧向力选用简化的魔术公式为
Fy=Dsin(Cαtan(Bα(1-E)+Eαtan(Bα)))
(5)
(6)
(7)
式中:Fy为轮胎侧向力;B为刚度因子;C为形状因子;E为曲率因子;α为轮胎侧偏角;αfl、αfr分别为前左右轮胎侧偏角;δ1、δ2分别为前左右轮转角(考虑左右轮转角差),魔术公式参数如表1所示。根据该表参数计算出样车轮胎侧向力与侧偏角的关系曲线,如图3所示。

表1 轮胎魔术公式参数
1.2.3 转向梯形间隙碰撞力
根据图2设间隙,沿x、y轴的分量分别为ex、ey,由几何关系可得:
(8)
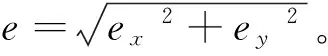
间隙接触角θ1可表示为
(9)
间隙中轴销相对轴套的法向与切向速度为:
(10)
(11)
(12)
在此假设轴销和轴套状态分为接触和分离两个状态,轴套表面有弹性和阻尼,因而当间隙副元素相接触时,会有接触力存在,为计算方便,把接触表面力-位移特性线性化处理,简化为弹簧-阻尼系统,其中轴套表面接触时的阻尼系数为C、刚度系数为K。
间隙副碰撞力法向力Fn和切向力Ft分别为
(13)
式(13)在x、y方向的分量为
(14)
式中:vn、vt为接触点轴销相对轴套的法向、切向速度;Fx、Fy分别为碰撞力在图2坐标系中x、y方向分量;f为摩擦因数;Cl为间隙大小。
从而得到间隙对主销的碰撞力矩Mc为
Mc=Fx(l1sin(γ-δ1)+ey)-Fy(l1cos(γ-δ1)-ex)
(15)
2 汽车转向稳定性数值计算与分析
以国产某小型客车作为样车,运用以上数学模型对间隙影响样车转向行驶稳定性数值计算。针对分析目标为转向行驶稳定性,本文中结合操纵稳定性的典型工况,采用恒定车速下转向盘阶跃力矩输入工况作为仿真工况进行离线仿真分析。计算所需样车的数据,见表2,获得间隙影响汽车转向行驶稳定性指标横摆角速度ω与质心侧偏角β,结果如图4~图6和表3所示。其中,图4取汽车稳态转向时ω、β时域响应计算间隙数值大小对其影响程度。
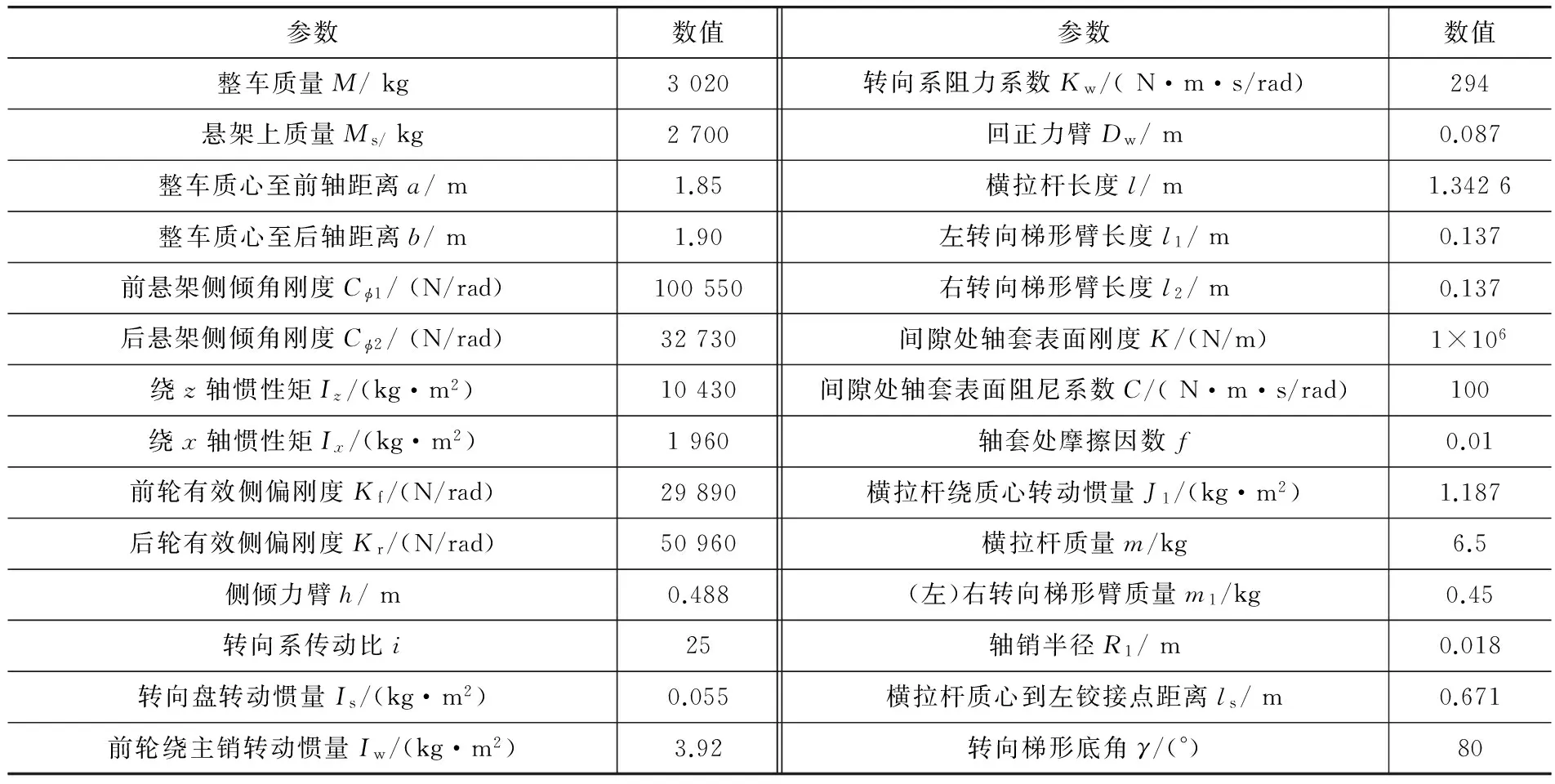
表2 样车计算主要参数

(ω,β)①②③④⑤⑥间隙为0.1mm(0.79,-1.05)(0.81,-1.03)(0.81,-1.01)(0.83,-0.99)(0.83,-0.97)(0.85,-0.95)间隙为0.5mm(0.79,-1.05)(0.81,-1.03)(0.81,-1.01)(0.81,-0.99)(0.83,-0.97)(0.83,-0.95)间隙为2mm(0.77,-1.05)(0.77,-1.03)(0.79,-1.01)(0.81,-0.99)(0.81,-0.97)(0.83,-0.95)
图4为汽车转向行驶时不同间隙对转向行驶横摆角速度与质心侧偏角影响的时域图。在图4(a)中,间隙为Cl=0.1mm时对汽车转向行驶时横摆角速度与质心侧偏角时域图响应影响很小;在图4(b)中,间隙为Cl=0.5mm时横摆角速度ω稳态振幅为2×10-3rad/s,质心侧偏角β稳态振幅为3.5×10-4rad;在图4(c)中,间隙为Cl=2mm时横摆角速度ω稳态振幅为1×10-2rad/s,质心侧偏角β稳态振幅为1.7×10-3rad。
由此可见,存在间隙时ω与β稳态值出现剧烈 波动,且随着间隙增加横摆角速度ω与质心侧偏角β稳态振幅数值逐渐加大,影响了车辆转向行驶的操纵稳定性品质。
图5为不同间隙时横摆角速度ω与质心侧偏角β相平面图及其局部放大图。由图5可见,考虑转向系间隙的汽车转向行驶失稳仍是鞍-结分岔[4,11]。间隙虽然没有改变转向行驶失稳的性质,但由图5的局部放大图和表3可见,随着转向机构间隙Cl由0.1、0.5和2mm逐步加大时,样车的ω-β相平面中稳定区域逐渐减小,加大了车辆在一定工况下转向行驶失稳概率。
在表3中,序号①~⑥是局部放大相图中的相点序号,即为稳定临界点的序号。每列有相同的纵坐标横摆角速度ω值,但随间隙的增大,横坐标质心侧偏角β值不断变小,表明临界点内移,在该工况下汽车转向稳定区域在减小。图6为对应表3的不同间隙时局部放大图中相空间区域变化图,各条线段代表不同间隙对应稳定区域和不稳定区域的分界线。分界线如图6中箭头所示随着间隙增大而左移,表明ω-β稳定区域随间隙增大而减小。
3 结论
(1)建立了考虑转向机构间隙的4自由度汽车操纵稳定性系统动力学模型。
(2)从横摆角速度与质心侧偏角的时域图和相图可以发现,随着转向机构间隙增加,ω与β的稳态响应振幅加大,响应品质变差;在ω-β相图中随着间隙增加,稳定区域逐减小。
(3)由以上数值分析可见,转向机构的间隙虽然没有改变汽车转向行驶时失稳的鞍-结分岔性态,但恶化了转向稳态响应的品质和减小了转向行驶稳定区域,因此,对转向机构的运动副间隙大小应相应控制,有利于提高车辆转向行驶稳定性。
[1] 郭孔辉. 汽车操纵动力学[M]. 长春:吉林科学技术出版社,1991.
[2] Pacejka H B. Tyre and Vehicle Dynamics[M].Oxford: Butterworth-Heinemann, 2002.
[3] Gillespie T D. Fundamental of Vehicle Dynamics[M]. Warrandale of USA: Society of Automotive Engineers, Inc., 1992.
[4] Vincent N. Vehicle Handling, Stabiity and Bifurcation Analysis of Nonlinear Vehicle Models[D].University of Maryland, 2005.
[5] 施树明,毛振勇,向辉,等. 车辆转向的稳定性非线性分析方法[J].机械工程学报,2007,43(10):77-81.
[6] Ono Eiichi, Hosoe Shigeyuki, Tuan Hoang D, et al. Bifurcation in Vehicle Dynamics and Robust Front Wheel Steering Control [J]. IEEE Transactions on Control System Technology,1998, 6(3):412-420.
[7] Shen Shuiwen, Wang Jun, Shi Peng, et al. Nonlinear Dynamics and Stability Analysis of Vehicle Plane Motions[J]. Vehicle System Dynamics,2007,45(1):15-35.
[8] 刘丽. 车辆三自由度平面运动稳定性的非线性分析及控制策略评价 [D]. 长春:吉林大学,2010.
[9] 靳春梅. 含间隙机构非线性动态模拟控制及实验研究 [D]. 西安:西安交通大学,2001.
[10] 顾鴃. 考虑转向系间隙的汽车前轮摆振系统研究 [D].合肥:合肥工业大学,2007.
[11] 刘延柱,陈立群.非线性振动 [M]. 北京:高等教育出版社,2001.

