电动汽车用锂离子电池生热速率模型*
朱 聪,李兴虎,宋凌珺
(1.北京航空航天大学交通科学与工程学院,北京 100191; 2.交通运输部公路科学研究院,北京 100088)
前言
锂离子电池目前是电动汽车理想的能源储存装置之一。由于锂离子电池开路电压、可用容量和最大充放电功率等参数均受其温度影响[1],同时温度过高会加快电池性能的衰退,甚至引发热失控[2],因此建立能够准确预测锂离子电池温度变化的热模型,对于车用锂离子电池组的性能研究以及热管理系统的设计开发具有重要意义。
合理计算锂离子电池的生热速率是建立准确热模型的必需基础。目前锂离子电池热模型中广泛使用Bernardi方程[3]计算电池的生热速率,该方程计算简单,但是未考虑电池极片中反应电流密度、活性物质浓度等参数的空间差异。文献[4]中指出这种简化处理会导致电池生热速率的计算产生较大误差。文献[5]和文献[6]中在考虑极片中参数空间差异的前提下建立了锂离子电池的热模型,模型中均忽略了电池内生成的可逆热。但相关研究表明,可逆热在锂离子电池内部产生的全部热量中约占30%[7]。文献[8]和文献[9]中的研究结果也表明,在工作电流较小的情况下可逆热是锂离子电池内部的主要热源。
为能合理地计算锂离子电池的生热速率并探讨可逆热对锂离子电池温度的影响,在考虑极片中参数空间差异的前提下,本文中建立锂离子电池的生热速率模型,并通过对比电池温度的仿真结果与实测结果,分析可逆热在不同工况下对电池温度的影响,为建立精确的锂离子电池热模型提供理论基础。
1 生热速率模型
1.1 模型控制方程
1.1.1 模型基本假设
图1为锂离子电池的主要组成结构,包括正负极极片、正负极集流体和隔膜。其中正负极极片的活性物质颗粒分别为LiMn2O4和LixC6,电解液溶剂为碳酸乙烯酯/二甲基碳酸酯组成的混合溶剂,电解质盐为LiPF6。正负极片和隔膜的厚度分别以δ+、δ-和δsep表示,L则表示三者之和。
大量研究成果表明,锂离子电池充放电过程中内部的生成热主要为反应热、欧姆热和极化热[8,10-13],其中反应热为可逆热,欧姆热和极化热为非可逆热。考虑到锂离子往返于电池正负极片时总是寻找阻力最小的传输路径,而集流体的电导率又远大于极片和电解液的电导率,因此可以认为反应电流密度、活性物质浓度等参数仅在电池极片厚度方向上存在差异[14],故本文中在计算锂离子电池的生热速率时仅考虑电池参数沿极片厚度方向的变化。
以负极极片与负极集流体交界处为原点,极片厚度方向为x轴正方向建立图1所示一维坐标系,并不失一般性地假设:(1)电极中活性物质颗粒分布均匀且为半径相等的球体颗粒;(2)固相颗粒中锂离子的扩散系数为常数,不随锂离子浓度变化;(3)充放电过程中电池极片体积、孔隙率的变化可忽略;(4)电池内部不发生副反应。
1.1.2 可逆热控制方程
由于反应物与生成物之间存在能量差别,电化学反应进行时总需要吸收或释放一部分热量以维持整个反应的能量平衡,这部分热量即称为反应热。如锂离子在电池某荷电状态(SOC)下发生的脱嵌反应为放热反应,在同样条件下锂离子发生的嵌入反应则必为吸热反应。因此锂离子电池的反应热为可逆热,其生成速率的大小与反应前后电极体系产生的熵变成正比。为便于表述,规定生热速率的符号为正、负时分别表示放出和吸收热量,则锂离子电池充放电时可逆热的生成速率均可由下式计算:
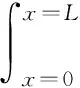
(1)
式中:Qrev为锂离子电池内部可逆热的生成速率,W;Se为电池极片的总面积,cm2;T为电池温度,K;j为固相与溶液相界面处净反应电流的体积密度,A/cm3,规定锂离子脱嵌时j>0,嵌入时j<0;ΔS为进行还原反应(嵌入反应)后电极体系产生的熵变,J/(mol·K)。
根据电化学热力学原理可知:
ΔS=(∂U/∂T)nF
式中:U为电池处于开路状态时的电极电势,称为平衡电极电势,V;n为锂离子所带电荷数,n=1;F为法拉第常数,F=96 487C/mol。∂U/∂T值主要取决于锂离子电池的SOC,一般通过实测电池在某固定SOC下U随电池温度的变化过程确定[10]。
图2给出了活性物质颗粒分别为LiMn2O4和LixC6的正负电极体系进行还原反应时,∂U/∂T值随电极化学计量比θ的变化情况[9]。
从图中可以看出,同样量的锂离子在不同θ下完成脱嵌或嵌入时电极体系产生的熵变大小不同。θ的数值等于cse/csmax,cse为活性物质颗粒表面的锂离子浓度,csmax为颗粒中锂离子的最大浓度,mol/cm3。以活性物质颗粒中心为原点建立球坐标系,则锂离子电池进行充放电时锂离子浓度的动态变化为
(2)
其边界条件为
(3)
式中:cs为活性物质球体颗粒中某处的锂离子浓度,mol/cm3;r为该处至球体颗粒中心的距离,cm;Ds为颗粒中锂离子的扩散系数,cm2/s,Rs为球体颗粒的半径,cm;se为单位体积电极所具有的活化面积,cm2/cm3。
1.1.3 非可逆热控制方程
电子在固相内、集流体内和固相与集流体之间进行传输时,以及锂离子在溶液相中进行传输时均会与构成传输介质的粒子发生碰撞,碰撞过程中产生的热量统称为欧姆热。在电池物性参数确定的前提下,欧姆热的生成速率与电子和锂离子的传输通量成正比。由欧姆定律可知,锂离子电池固相中电子的传输过程可描述为
(4)
其边界条件为
(5)
式中:σeff为固相有效电导率,S/cm;φs为固相电势,V;I为电池工作电流,A,规定电池充电时I>0,放电时I<0。
溶液相中由于需要考虑锂离子在浓度梯度作用下产生的扩散通量,不能直接利用欧姆定律计算锂离子的传输通量。根据浓溶液理论对欧姆定律进行修正后即得出溶液相中锂离子的传输过程[15]为
(6)
其边界条件为
∂φe/∂x|x=0=∂φe/∂x|x=L=0
(7)

(8)
其边界条件为
∂ce/∂x|x=0=∂ce/∂x|x=L=0
(9)

另外,由于集流体本身具有很高的电导率,文献[5]和文献[6]中均认为集流体内部的欧姆热可以省略,集流体与极片界面上欧姆热的生成速率可直接利用焦耳定律确定为I2Rc,Rc为电池集流体与极片之间总的接触电阻,Ω。故锂离子电池欧姆热的总生成速率Qo计算式为
(10)
从式中可以看出,与欧姆热生成速率相关的运行参数主要有电流等级、电势梯度和浓度梯度。而在电流等级一定的前提下,由式(4)和式(6)可知电势梯度、浓度梯度又主要由电导率和扩散系数决定。
电池处于开路状态时,锂离子在固相和溶液相界面上完成脱嵌和嵌入所须克服的活化能垒相等。只有打破两相界面上的能垒平衡,电极区域才能产生净反应电流。这部分用于打破能垒平衡的能量最终以热量的形式释放出来,即为锂离子电池的极化热,其生成速率为
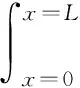
(11)
式中:Qp为锂离子电池极化热的生成速率,W;η为活化过电势,用于表征两相界面上锂离子完成脱嵌与完成嵌入所须克服的能垒之差,V。j与η之间的关系为
(12)
其中i0=kFceαa(csmax-cse)αacseαc
(13)
式中:αa、αc分别为阳极和阴极电子传递系数;R为通用气体常数,R=8.314J/(mol·K);RSEI为电极表面钝化膜的面比电阻,Ω·cm2;i0为交换电流密度,A/cm2;k为电极反应速率常数,cm2.5/(mol0.5·s)。
从式(11)中看出,与极化热生成速率相关的运行参数主要为电流等级和活化过电势。而在电流等级一定的前提下,由式(12)可知活化过电势的变化主要由交换电流密度i0决定,i0的取值则与活性物质颗粒的表面浓度和最大浓度(即电池SOC)相关。
1.2 模型求解流程
电流等级、初始SOC和初始温度为锂离子电池生热速率模型的输入参数。将图1所示总长度为L的电极和隔膜区域沿x轴依次分为N个控制体,各控制体中反应电流密度的空间差异可忽略不计,控制体长度为Δx=L/N。结合各方程的边界条件和初始条件,由下述流程即可计算锂离子电池t时刻的生热速率:
(a) 限定t时刻第1个控制体边界面(即x=0)处的固相电势φs(t,0)=0,并对同一界面处的溶液相电势φe(t,0)假设一个初始值;
(b) 利用(t-Δt)时刻的cse/csmax值求得平衡电极电势U(t,0)和交换电流密度i0(t,0),并求出活化过电势η(t,0)=φs(t,0)-φe(t,0)-U(t,0),然后利用式(12)即可确定控制体1中的反应电流密度j(t,1);
(c) 将j(t,1)代入式(4)和式(6)便可求得t时刻x=Δx处的φs(t,Δx)和φe(t,Δx)值,此时再利用步骤(b)即可确定控制体2中的j(t,2)值;
(d) 以同样的方法获得电池整个负极区域控制体中的j、φs、φe和U后,再检验负极区域所有控制体中j的总和与-I之间的相对误差是否低于设定值,如低于设定值则t时刻负极区域各参数的求解完毕,如高于设定值则需对φe(t,0)假设的初始值进行调整,按同样流程重新求解各项参数,直至满足结束条件为止;
(e) 将求得的φe(t,δ-)代入式(6)便可得到t时刻x=L-δ+处的φe(t,L-δ+)值,此时再对该界面处的φs(t,L-δ+)假设一个初始值,同样通过迭代调整该初始值便可确定电池正极区域控制体中各项参数的合理值;
(f) 将所求得的参数逐个代入式(1)、式(10)和式(11)中的对应项,即可得出锂离子电池t时刻可逆热和非可逆热的生成速率。
最后分别利用式(2)和式(8)更新各控制体中的cse和ce值,重复步骤(a)~(f)即可计算(t+Δt)时刻锂离子电池的生热速率。需要注意的是,由于电池隔膜区域内不发生电化学反应,在x=δ-~L-δ+的计算域内恒有j=0,φs=0。
2 仿真与试验结果分析
2.1 生热速率计算
以正极材料为锰酸锂的3.6V/8A·h方形锂离子电池为建模对象,使用第1.2节中所述的流程对电池在不同工况下运行时的生热速率进行模拟计算。图3给出了锂离子电池在SOC为50%进行充放电时,电流可逆热生成速率的模拟值Qrev和非可逆热生成速率的模拟值Qirr随电流等级的变化情况,其中Qirr=Qo+Qp。图4中则给出了电池以10C的电流进行充放电时Qrev和Qirr随电池SOC的变化。
从图3中看出,Qrev和Qirr的大小均随电池充放电电流的增大而增大,但Qrev随电流的增速基本不变,Qirr随电流的增速则逐渐提高。这是因为随着电池充放电电流的增大,两相界面上产生的净反应电流密度也随之增大,进而导致两相界面上的活化过电势以及电势梯度、浓度梯度也都随之增大。假设极片中体积为ΔV的某一微元控制体内反应电流密度增大Δj,对应活化过电势增大至η′,固相电势梯度增大至(∂φs/∂x)′,则由第1.1.2节中所述可知该控制体中可逆热的生成速率增大ΔjT(∂U/∂T)ΔV,由第1.1.3节中所述可知该控制体中非可逆热的生成速率增大Δj[(∂φs/∂x)′Δx+η′]ΔV。因此随着电池充放电电流的增大,可逆热生成速率的大小与电流成正比,但非可逆热生成速率随电流的增幅则随着电流的增大逐渐提高。
从图4中可以看出,电池SOC的变化对Qrev有较大影响,相对而言对Qirr则无显著影响。当锂离子电池充放电电流一定时,电极体系在不同SOC下产生的熵变不同,两相界面上的交换电流密度也不一样,因此反应热和极化热的生成速率均随电池SOC变化。但是由于极片与集流体之间接触电阻所贡献欧姆热的生成速率不受SOC影响,并且远大于极化热的生成速率,因此非可逆热总的生成速率随电池SOC并无明显变化。
另外图3和图4中结果均表明,充电时Qirr随SOC和电流的变化曲线与放电时Qirr的变化曲线基本重合,充放电时Qrev的变化曲线则基本对称分布。这是因为锂离子电池在相同SOC和电流下进行充电和放电时极片中产生的反应电流密度、电势梯度等参数基本都一致,电极体系熵值的变化量也基本相同,但充放电时电极体系熵值的变化方向恰好相反。因此,充放电时非可逆热的生成速率基本相等且均表现为放热;可逆热的生成速率也基本相等但分别表现为吸热和放热。
2.2 可逆热对电池温度的影响
在生热速率和比热容一定的情况下,锂离子电池内部的温度差异与其导热热阻成正比。而电池的导热热阻又与其结构特点相关,如电池导热面积越大、导热距离越短,其导热热阻便越小,电池内部形成的温度差异便越小。本文建模对象的长、宽和厚为190、120和8mm,该结构特点(侧面积/厚度=2 850)使电池整体具有较好的温度均匀性。因此,对锂离子电池温度进行仿真计算时可以假设电池内部的温度均匀分布。利用锂离子电池生热速率的模拟值,由式(14)即可计算电池在不同工况下运行时其温度的动态变化过程:
(14)
式中:Qgen为锂离子电池生热速率,W;cbat为电池比热容,J/(kg·K);mbat为电池质量,kg;hcom为电池表面的综合换热系数,W/(m2·K);Acom为电池综合换热表面的总面积,m2;Tamb为环境温度,℃。
为了验证锂离子电池生热速率模型的有效性,并考察可逆热对电池温度变化的影响程度,以电池侧表面中心为温度测点,基于Arbin台架测量了3.6V/8A·h方形锂离子电池进行恒流放电、恒流充电和交替充放电时电池温度的动态变化过程。考虑到电池在大电流工况下运行时的温升速率较大,因此将电池置于0℃的低温环境中进行试验,以确保试验过程中电池温度不超过允许的最大限值。
图5(a)为电池进行1C、5C恒流充电时,电池实测温度Texp和模拟温度Tbat1、Tbat2随SOC的动态变化,Tbat1和Tbat2为Qgen分别等于Qirr+Qrev和Qirr时利用式(14)得出的模拟结果;图5(b)则为电池进行1C、5C恒流放电时Texp、Tbat1和Tbat2随放电深度(DOD=100%-SOC)的变化情况。从图中可以看出,电池分别以1C、5C的电流进行恒流充放电时,Texp与Tbat1在不同SOC和DOD下的最大偏差均不超过1℃;而Texp与Tbat2之间则存在较大偏差,尤其是电池进行1C恒流充电时,二者的最大偏差已超过4℃。这说明锂离子电池在进行持续充放电的情况下,可逆热对电池温度存在较大影响,并且这种影响在电池充放电流较小时更为明显。由图3可知,产生这一现象是因为在小电流工况下可逆热与非可逆热生成速率的大小相当,而在大电流工况下非可逆热则逐渐成为主要热源,导致可逆热对电池温度变化的影响相对减小。
图6给出了电池初始SOC为50%时分别以1C、5C的电流循环进行充放电,Texp、Tbat1和Tbat2的变化过程。充放电循环与HPPC复合脉冲试验[16]类似,在每个循环中首先进行恒流放电10s,静置40s后再恒流充电10s。从图中可以看出,电池在不同电流下交替充放电时Texp与Tbat1、Tbat2均吻合得较好,表明此时可逆热对电池的温度变化不存在明显影响。由图4可知,这是因为电池相同SOC下进行充放电时的可逆热分别表现为吸热和放热,因此电池在某一SOC附近交替充放电产生的可逆热在一定程度上相互抵消,削弱了可逆热对电池温度变化的影响。此处需要说明的是,试验电池分别以不同初始温度进行恒流放电、恒流充电和交替充放电后均得出了类似的结论。为了避免电池在不同工况下的温升曲线相互叠加,在图5(b)和图6中均特别选取了初始温度不同的温升曲线进行对比。
3 结论
(1) 本文中建立的锂离子电池生热速率模型考虑了极片中反应电流密度、活性物质浓度等参数的空间差异,模型能对锂离子电池可逆热和非可逆热的生成速率进行合理计算,利用模型的计算结果可以有效模拟电池温度的瞬态变化过程。
(2) 模型仿真结果表明,可逆热与非可逆热的生成速率均随锂离子电池充放电电流的增大而增大,但前者随电流的增速基本不变,后者则随电流的增速逐渐提高;电池SOC的变化主要影响可逆热的生成速率,对非可逆热的生成速率无显著影响;电池在相同SOC和电流下分别进行充电和放电时,非可逆热的生成速率基本相等且均表现为放热,可逆热的生成速率也基本相同但分别表现为吸热和放热。
(3) 仿真与试验结果表明,锂离子电池持续进行充电或放电时,可逆热对电池的温度变化存在较大影响,并且这种影响在充放电电流较小时尤为明显;而电池在某一SOC附近交替进行充放电时,可逆热对电池温度的影响并不明显。
[1] Belt Jeffrey R, Ho Chinh D, Miller Ted J, et al. The Effect of Temperature on Capacity and Power in Cycled Lithium-ion Batteries[J]. Journal of Power Sources,2005,142:354-360.
[2] Selmana J Robert, Hallaja Said Al, Uchidab Isamu, et al. Cooperative Research on Safety Fundamentals of Lithium Batteries[J]. Journal of Power Sources,2011,97-98:726-732.
[3] Bernardi D, Pawlikowski E, Newman J. A General Energy Balance for Battery Systems[J]. Journal of Electrochem. Soc.,1985,132(1):5-12.
[4] Rao Lin, Newman John. Heat Generation Rate and General Energy Balance for Insertion Battery Systems[J]. Journal of Electrochem. Soc.,1997,144(8):2697-2704.
[5] Smith Kandler, Wang Chaoyang. Power and Thermal Characterization of a Lithium-ion Battery Pack for Hybrid-electric Vehicles[J]. Journal of Power Sources,2006,160:662-673.
[6] Fang Weifeng, Kwon Ou Jung, Wang Chaoyang. Electrochemical-thermal Modeling of Automotive Li-ion Batteries and Experimental Validation Using a Three-electrode Cell[J]. International Journal of Energy Research,2010,34:105-107.
[7] Zhang Xiongwen. Thermal Analysis of a Cylindrical Lithium-ion Battery[J]. Electrochimica Acta,2011,56:1246-1255.
[8] Dong Hyup Jeon, Seung Man Baek. Thermal Modeling of Cylindrical Lithium Ion Battery During Discharge Cycle[J]. Energy Conversion and Management,2011,52:2973-2981.
[9] Ye Yonghuang, Shi Yixiang, Cai Ningsheng, et al. Electro-thermal Modeling and Experimental Validation for Lithium Ion Battery[J]. Journal of Power Sources,2012,199:227-238.
[10] Christophe Forgez, Dinh Vinh Do, Guy Friedrich, et al. Thermal Modeling of a Cylindrical LiFePO4/graphite Lithium-ion Battery[J]. Journal of Power Sources,2010,195(9):2961-2968.
[11] Noboru Sato. Thermal Behavior Analysis of Lithium-ion Batteries for Electric and Hybrid Vehicles[J]. Journal of Power Sources,2001,99(1-2):70-77.
[12] Viswanathan Vilayanur V, Choi Daiwon, Wang Donghai, et al. Effect of Entropy Change of Lithium Intercalation in Cathodes and Anodes on Li-ion Battery Thermal Management[J]. Journal of Power Sources,2010,195(11):3720-3729.
[13] Jiang Zhiyu, Zhang Jie, Dong Liangjun, et al. Determination of the Entropy Change of the Electrode Reaction by an AC Electrochemical Thermal Method[J]. Journal of Electroanalytical Chemistry,1999,469(1):1-10.
[14] Gu W B, Wang C Y. Thermal-electrochemical Modeling of Battery Systems[J]. Journal of Electrochem. Soc.,2000,147(8):2910-2922.
[15] Doyle Marc, Newman John. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells[J]. Journal of the Electrochemical Society,1996,143(6):1890-1903.
[16] Freedom CAR Battery Test Manual for Power-Assist Hybrid Electric Vehicles[M]. Idaho National Engineering and Environmental Laboratory,2003:89-93.

