基于小波奇异性检测的发动机故障诊断方法研究*
肖云魁,乔 龙,张玲玲,2,赵慧敏,杨青乐
(1.军事交通学院汽车工程系,天津 300161; 2.军械工程学院火炮工程系,石家庄 050003)
前言
信号的奇异点往往包含故障引起的撞击、振荡、摩擦和结构变形等重要信息[1]。二进离散小波变换不但可以准确地确定奇异点的位置,而且可以检测信号奇异性特征[2]。数学上常用Lipschitz指数来定量描述信号的局部奇异性[3],然而通过二进离散小波变换计算出的Lipschitz指数不够精确且不含有与故障程度密切相关的能量信息,模极大值的平方和指示能量的物理意义则更明确[4]。本文中提出了模极大值点能量的概念来描述某一段信号的奇异性,并应用到发动机曲轴轴承的故障诊断中。
发动机激励源众多[5],从机体上所得到的振动信号是内部多个运动部件综合激励的结果。仅从振动信号来判断故障存在一定的困难。某些部件在工作中对系统施加的冲击力与配气相位密切相关,因此通过提取特定时间段的信息(抽区间采样),对其进行分析可以有效实现特定部件运行状态信息的的分离,提取出故障信号特征。
1 小波奇异性检测原理
对信号进行奇异性检测包括对奇异点的定位和确立奇异性指标的大小两个方面[6]。
1.1 奇异点的定位
设ψ(t)是小波母函数。当分析机械振动信号时,一般可选择具有二阶消失矩的小波函数[7],本文中选择db2小波作为小波母函数。函数f(t)∈L2(R)关于ψ(t)的二进离散小波变换为
(1)
式中:2j为小波变换尺度;W为小波变换系数。当小波变换尺度为s时,如果存在一点b0,使b0的某一邻域内的任意点b,均有|Ws(b,ψ(t))|≤|Ws(b0,ψ(t))|,则称(s,b0)为小波变换的模极大值点[8],它与f(t)的奇异点存在对应关系,Ws(b0,ψ(t))是小波变换模极大值。
在低尺度下小波变换的模极大值点与突变点对应准确,但容易受噪声的影响产生许多伪极值而影响判断;随着尺度的增加,噪声的小波变换幅度以指数规律迅速衰减[9-10],由于机械振动信号的峰值点和突变尖点的Lipschitz指数通常为正[1],其小波变换的幅值随尺度的增加而增加,从而分离出模极大值点和噪声,但大尺度下模极大值点对奇异点的定位相对较差。因此,须进行多尺度分析方可有较好的效果。
1.2 奇异性指标的确立
二进离散小波变换为了使变换具有时不变性,只作尺度上的二进离散,对不同尺度上的时间参数进行等间隔采样。然而,尺度区间的二进离散在许多情况下显得过于粗糙,从而计算出的Lipschitz指数不够精确,不能很好地区分是正常点还是异常点[4],而且用Lipschitz指数不能区分同类型但突变程度不同的突变点。而求取可以指示能量大小的模极大值的平方和,计算简单且物理意义更明确。因此,可用信号模极大点的能量之和来描述该信号整体的奇异性,能量之和越大,说明整体信号奇异性越强,反之则越小。
模极大值点能量之和为
(2)
式中:f为待分析的信号;s为小波变换的尺度;N为模极大值点的点数;ti为第i个模极大值点出现的时刻;ψ为小波母函数;W为模极大值。
2 仿真算例
本文中以一个含有3个阶跃信号的函数f0(t)为例,加入高斯白噪声fnoise(t)建立仿真信号f(t):
f(t)=f0(t)+fnoise(t)
fnoise(t)为加入的信噪比为35db的白噪声,时域波形如图1(a)所示。从信号定义和时域波形可以看出,信号在时刻32、64、128处是突变点,在时刻128处突变程度是32和64处的2倍。而理论上冲击点的Lipschitz指数均为0。选用db2小波作为母函数,小波变换尺度为21、22、23,经过计算得到奇异点的Lipschitz指数均为0.098 3。所以利用二进离散小波变换得出的Lipschitz指数作为振动信号的奇异性指标不够精确;而且未能体现出信号奇异点的能量。
下面采用模极大值点能量|Wsf(ti,ψ)|2来衡量信号的奇异性。选用db2小波对其进行3层小波分解,分解尺度为21、22、23的模极大值点分别如图1(b)~图1(d)所示。
由图可见:在分解尺度为21时由于噪声较多,模极大值图中产生了许多伪极值点,不能正确判断出奇异点的位置;当分解尺度增加到22时噪声点数明显减少,可以清晰地看出突变点的位置,并且时刻128点处模极大值大约是时刻32和64处的2倍,说明时刻128处的能量是其他两点处的4倍;但是当尺度继续增大到23时,奇异点的位置开始发生较为明显的偏移,这是因为小波变换计算过程是信号与小波函数进行卷积运算的过程,当小波函数尺度较大时,信号的时域分辨率较差造成对奇异点定位不准确。因此采用模极大值点的能量来描述奇异性时,在多尺度下综合分析不仅能精确指出奇异位置,而且可以衡量奇异点能量的大小。
3 实例分析
3.1 试验设置
本文中以东风EQ2102型柴油发动机作为研究对象,选取第4道曲轴轴承为试验轴承,分别设置不同曲轴轴颈与轴承配合间隙以模拟各种磨损状态。由于曲轴具有很高的刚度,当仅有1道轴承间隙增大时,它承担的载荷会减小,相邻的轴承分担的载荷增大,随着发动机的运转,相邻轴承的间隙也会发生相应的变化。为了更加符合实际情况,同时设置第3、4、5道曲轴轴承为故障轴承。故障设置情况如表1所示。
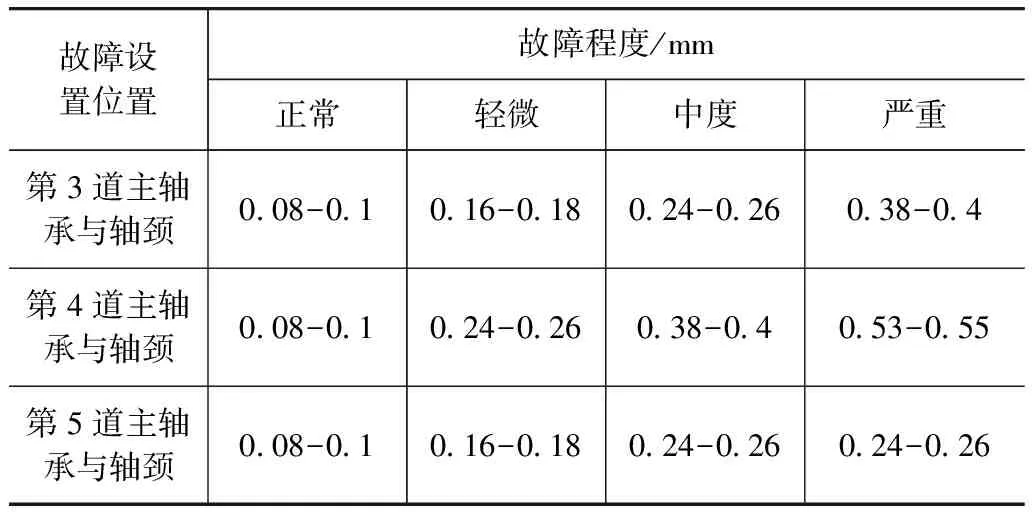
表1 发动机曲轴轴承不同配合间隙设置
测量发动机在曲轴轴承不同配合间隙条件下不同测点的振动信号,测点a~d分布如图2所示,4个测点与第4道曲轴轴承在一个平面内。同时采集飞轮壳齿圈脉冲信号和第1缸喷油压力信号分别用以计算发动机转速和抽区间采样,采集发动机各缸上止点信号,发动机空载运行。为了确定最佳故障诊断转速,选择800、1 300、1 800和2 100r/min为试验转速。采样频率设置为20kHz。
3.2 抽区间采样
抽区间采样是采集对应于发动机每一循环中特定时间段内的振动信号,与某个感兴趣的瞬态冲击力相对应,然后采用一些分析方法进行特征提取[3]。对于发动机某一道曲轴轴承的故障来说,它对应的气缸做功时故障特征会表现得更为明显。同时为了保证数据的稳定性,抽取发动机连续4个工作循环第4缸做功阶段的信号进行分析。下面以发动机正常工况下转速为1 800r/min时测点b处的振动信号为例,说明抽区间采样的过程:
(1) 连续寻找5个喷油时刻 设定一个阈值,当喷油压力信号的幅值大于该值时即认为该点为喷油时刻(本文中设定1为阈值),连续寻找5个喷油时刻,如图3(a)所示,则每2个喷油时刻之间发动机完成了一次工作循环;
(2) 抽取连续4个工作循环的振动信号 由于该型发动机喷油提前角为20°,将振动信号中5个喷油时刻间的数据往后推移74个数据点(采样频率为20kHz,发动机转速为1 800r/min时喷油提前角对应约74个数据点),即为发动机连续4个工作循环的振动信号,如图3(b)所示,双箭头标注为做功序号(下同);
(3) 抽取连续4个工作循环中第4缸做功阶段的振动信号 根据6缸发动机做功顺序:1-5-3-6-2-4,将通过步骤(2)抽取的每一工作循环的振动信号平均分成6段,抽取最后一段作为第4缸做功阶段的振动信号(约为222个点),连接在一起完成抽区间采样,如图3(c)所示。
3.3 试验数据的分析
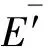
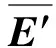
表2 曲轴轴承不同技术状态下对比
选择db2小波进行5层二进离散小波变换,提取每一层小波变换的模极大值点。转速为1 800r/min时测点b处不同技术状态下的模极大值如图5所示,限于篇幅图中只列出了小波变换尺度为21、23和25时的模极大值点。
由图可见:纵向分析,可以明显看出随着尺度的增加,模极大点的数目依次减少但幅值增加,说明噪声随着尺度的增加急剧衰减,而突变信号由于Lipschitz指数为正,模极大值随尺度的增加而变大,与噪声表现正好相反,因此随着尺度的增加噪声和奇异点得以分离;横向对比,随着曲轴轴承与轴颈配合间隙的增大,在同一尺度下总体上模极大值越来越大。除此之外,根据小尺度分解时模极大值点对奇异点定位精确的特点,从分解尺度为21的模极大值图中可以看出,当曲轴轴承出现磨损故障的情况下,每个做功阶段中第4缸开始做功时模极大值开始增大,如图5(b)~图5(d)中222点、444点、666点处左右。这是因为发动机运转过程中,当某一缸从压缩行程换至做功行程时活塞换向,而曲轴轴承与轴颈的配合间隙超出正常范围后,连杆带动曲轴旋转时对轴承的撞击加剧,表现为缸体信号奇异性增强。
图5中分解尺度为25时极大模值点的点数已经明显减少、幅值稳定,而且相对于小尺度分解时模极大值点的偏移程度可以接受,因此确定在该尺度下计算模极大值点能量之和进行奇异性分析。曲轴轴承每种技术状态下随机选取40组样本,每组样本的E值如图6所示。
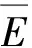

表3 曲轴轴承不同技术状态下对比
为了确定最佳测试转速,本文中利用同样方法对发动机在怠速800r/min、中速1 300r/min和高速2 100r/min时分别进行了分析,发现在中低速(800、1 300r/min)时信号的模极大值点平均能量与故障程度之间并没有规律,而在高速(2 100r/min)时与中高速(1 800r/min)一样有规律。这是由于发动机机体沉重,运转时其惯性与速度有很大关系,速度越高惯性越大,连杆带动曲轴旋转时对轴承的撞击越大,当速度较低时,撞击力小,经过缸体的低通滤波作用其奇异性并没有通过缸体信号体现出来。
同样本文中分析了发动机缸体右侧(测点c)和油底壳(测点d)、缸盖处(测点a)的振动信号的奇异性,都没有良好的规律性。这是由发动机的结构决定的:从发动机后方观察发动机运转时,连杆带动曲轴做逆时针旋转运动,当被测轴承对应的气缸开始做功时活塞下行,曲轴对轴承左侧形成瞬态强烈冲击,位于缸体外部左侧的振动传感器正好捕捉到这一信号。当曲轴撞击轴承右侧时,气缸已完成做功行程,撞击已经明显减弱。而油底壳和缸盖由于距离激励源较远,信号的奇异性也不显著。
4 结论
(1) 利用模极大值点能量来描述信号奇异性的方法计算简单、意义明确,抽区间采样能有效缩短分析数据的长度,突出局部时间段的信号特征,两种方法的结合能有效区分出曲轴轴承的技术状态。
(2) 对发动机曲轴轴承进行故障诊断时,利用模极大值点能量进行奇异性检测的最佳转速是中高速,最佳诊断部位为发动机缸体左侧。
[1] 贺银芝,沈松,刘正士,等.基于小波变换的奇异性检测在发动机连杆轴承故障诊断中的应用[J].北京工业大学学报,2000,26(4):72.
[2] 庞茂,周晓军,胡宏伟,等.基于解析小波变换的奇异性检测和特征提取[J].浙江大学学报,2006,40(11):1994-1997.
[3] 林京,屈梁生.基于连续小波变换的奇异性检测与故障诊断[J].振动工程学报,2000,13(4):523-529.
[4] 余同辉,闫河,何莉,等.基于小波奇异性理论的输油管道泄漏检测与定位方法[J].计算机技术与应用,2009(9):135.
[5] 贾继德,陈荣钢,陈剑.基于抽区间采样的内燃机状态监测方法研究[J].内燃机工程,2005,26(6):72-75.
[6] 关山,胡全.小波奇异性检测理论在齿轮故障诊断中的应用[J].煤矿机械,2008,29(8):188-190.
[7] 褚福磊,彭志科,冯志鹏,等.机械故障诊断中的现代信号处理方法[M].北京:科学出版社,2009:58-70.
[8] 胡昌华,张军波,夏军,等.基于MATLAB的系统分析与设计[M].西安:西安电子科技大学出版社,1999:210.
[9] 李曙光,张梅军.小波去噪与奇异性检测相结合诊断动静件短暂碰磨故障发生区间[J].机械设计,2010,27(10):80.
[10] Anend K Soman, Vaidyanathan P P. On Othormormal Wavelates and Paraunitary Filter Banks[J]. IEEE Trans. S. P.,1993,41(3):1170-1183.

