基于LMS和SDP的发动机异响诊断方法研究
杨 诚,李 爽,冯 焘,杨振东
(1.重庆大学机械工程学院,重庆 400044; 2.重庆建设摩托技术中心,重庆 400054)
前言
发动机往往会在生产中由于配件质量或装配问题而产生非正常的振动和异响[1]。目前,我国对发动机异响的诊断主要还是靠人耳辨别发动机的声音特征[2],该方法具有一定的主观性,易出现错检、漏检,对生产效率和整车质量造成了严重的影响,所以需要一种更加科学有效的方法对发动机异响进行诊断。
本文中采用发动机声信号作为异响诊断信号,避免了振动信号的不足[2]。运用最小均方(LMS)算法对含有背景噪声的声信号进行降噪处理,可以较好地去除背景噪声,还原发动机声信号[3]。另外,由于发动机声信号是一种典型的时变非平稳信号[4],采用传统的时域和频域分析方法很难满足特征提取与模式识别的要求,故本文中利用人眼对对称特征的敏感性[5]提出了一种采用对称点图形(SDP)的噪声特征提取方法。该方法将信号特征用对称点图形表示,可以很好地突出信号间的差异。
将LMS算法与SDP相结合的发动机异响诊断方法可以很好地识别发动机状态。
1 最小均方(LMS)算法
最小均方(LMS)算法[6]是在维纳滤波的基础上,提出来的一种自适应滤波法,它具有结构简单、计算复杂度低、收敛性好、性能稳定等优点,因此被广泛应用。LMS算法基本流程如下:
滤波输出y(n)=wT(n)x(n)
(1)
误差信号e(n)=d(n)-y(n)
(2)
权系数更新w(n+1)=w(n)+μe(n)x(n)
(3)
式中:x(n)为输入信号;w(n)为权系数;d(n)为期望响应;μ为系数更新步长。
1.1 维纳霍夫方程与维纳解
由于式(2)中误差信号e(n)是一个随机变量,采用最小均方误差准则作为滤波准则,可以比较简单地评判滤波器输出信号与期望信号之间的差异,即
J(n)=E{e2(n)}
(4)
假设滤波器的系数为wk,则系统的输出误差为
e(n)=d(n)-y(n)=d(n)-wTx(n)
(5)
将式(5)代入式(4),可得:
J(n)=E{d2(n)}-2E{xT(n)d(n)w}+
E{wTx(n)xT(n)w}
(6)
设x为滤波器输入信号与期望响应的互相关向量,定义为P=E{x(n)d(n)};设R为输入信号的自相关矩阵,定义为R=E{x(n)xT(n)}。
将P、R代入式(6)得
J(n)=E{d2(n)}-2PTw+wTRw
(7)
由式(7)可知,均方误差是滤波器权系数w的二次方程,对w求导,可求出均方误差的最小值为
∂J(n)/∂w=-2P+2Rw
(8)
假定R是非奇异矩阵,并令式(8)等于零,可得:
w0=R-1P
(9)
式(9)即称为维纳-霍夫方程[7]。w0是这一组滤波器系数的最优解,称为维纳解。
1.2 维纳解的估计
由式(9)可知,求维纳解须对输入信号的自相关矩阵R求逆,这就要用到信号的统计值,且当阶数较大时,计算量将大大增加,求解很难实现。因此,文献[6]中提出了以瞬时误差信号平方的梯度作为均方误差函数梯度的估计。
(10)
由于E{e2(n)}是E{e2(n)}的无偏估计,所以式(10)的新全矢量为
w(n)+μe(n)x(n)=
(I-μx(n)xT(n))w(n)+μx(n)d(n)
(11)
因为x(n)和w(n)不相关,故有
E{w(n+1)}=(I-μR)E{w(n)}+μP
(12)
所以E{w(n)}变化规律将沿着确定性轨迹,终止于维纳解w0[8-10],LMS算法的信号流程图如图1所示。
2 对称点图形(SDP)的概念与算法
对称点图形(SDP)技术可将信号特征用可视化的图形表示。它将信号的时域特征,通过公式计算,变为由镜像对称点组成的雪花状对称图形。利用该图形可突出信号间的差异性,表征信号的特征[11]。
2.1 对称点图形算法
图2为对称点图形原理图,它建立在极坐标S(r(i),Θ(i),Φ(i))中。其中r(i)为极坐标的极径,Θ(i)为极坐标中沿对称平面逆时针偏转的角度,Φ(i)为极坐标中沿对称平面顺时针偏转角度,其计算公式如下:
(13)
(14)
(15)
式中:i为信号采样点;xmax为信号最大幅值;xmin为信号最小幅值;l为间隔参数(通常取1~10);θ为镜像对称平面旋转角(该值为60m,其中m=1,…,6);ξ为放大因子[5]。
ξ与l应选择合理的数值,以提高图形特征的分辨率,选取方法可参考文献[12]。
2.2 对称点图形匹配系数r(A,B)
通过描述对称点图形与匹配模板间的相似程度,可建立一种发动机异响的评价方法。这里采用图形相关系数,即匹配系数来计算图形间的相似度。两个图形的匹配系数r(A,B)为
(16)
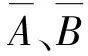
3 仿真分析
为了验证该算法的可行性与有效性,利用自回归模型(autoregressive model)建立了10阶的仿真信号AR(10),其计算公式为
(17)
式中:φj为AR模型的参数;εt为添加的白噪声;p为该模型的阶数。这里,AR模型参数设置为[5.32,-9.29,7.09,-2.81,2.58,-2.42,0.37,2.26,-0.30,-1.74,1.10]。信号的采样频率为4 096Hz,采样时间为1s。该AR(10)信号的时域与频域响应如图3所示。
在图3中,虚线为无噪声的理想信号,它含有3个主要频率成分,分别为300、700和1 400Hz。从频谱图中可见,无噪声的理想信号中重要的频率成分1 400Hz被白噪声所掩盖,所以无法准确得到SDP图像。为了得到全部频率成分,并提高信号的信噪比,在信号的降噪与特征提取中采用了LMS算法。
图4为降噪前后的时域与频谱响应图。从时域图中可见,LMS算法可在很短的时间内提高信号的信噪比。因此该算法可有效地运用到在线检测中。从频谱图中可见,降噪后的频谱能够有效地反映原始信号的全部特征。该频谱也与图3中无噪信号的频谱形状一致。同时,图5为降噪前后的SDP图形。由图可见,降噪后的信号图像特征与降噪前有很大的差异,说明SDP图形可以有效地反映信号特征的变化。
4 试验分析
以JY110型单缸四冲程发动机作为试验样机,利用上述方法对发动机异响进行研究与分析。这里选取状况正常和缸体右侧有异响的两类发动机。其中,发动机缸体右侧的异响主要是由离合器传动齿轮和机油泵装配误差或齿形误差引起的。
试验设备包括:发动机测试台架、测功机、PCB传声器、LMS(SCR01)数据采集前端、转速传感器和LMS Test Lab测试软件。数据采集参数设置:采样频率32 768Hz,采样时间为2s。在1 500r/min、空载状态下测量图6中所示A处的声信号,并从采集的信号中截取1s进行处理分析。
4.1 降噪前后SDP图形的比较
先选取1台典型的正常发动机和1台典型的缸体右侧有异响的发动机进行声信号测取和处理,其降噪前后的SDP图形分别如图7和图8所示。由两图对比可见:降噪前,正常发动机与缸体右侧有异响发动机的SDP图形基本一致,都有较明显的“花瓣”,只是线条粗细不同,没有显著的差别,因而难以区分;降噪后,正常发动机的SDP图形依然没有改变,只是线条更细一些,而缸体右侧有异响发动机的SDP图形则完全改变了,与降噪前相比有了明显的差别,这说明LMS算法对发动机声信号起到了良好的降噪作用,而SDP图形能够有效识别发动机是否产生异响。
4.2 SDP图形的匹配
为了客观验证SDP图形特点的一致性,将另外3台正常发动机(编号①,②,③)和3台缸体右侧有异响发动机(编号④,⑤,⑥)进行降噪处理,降噪后的SDP图形如图9和图10所示。
从图9和图10可以看出,3台正常发动机降噪后的SDP图形和3台缸体右侧有异响发动机降噪后的SDP图形各自都很相似,而图9和图10的图形却差异明显。
接着进一步将这6个SDP图形分别与图7(b)和图8(b)的典型SDP图形进行匹配分析,其结果如表1和表2所示。由表1可见,3台正常发动机与典型正常发动机SDP图形的匹配系数都明显大于其与典型缸体右侧有异响发动机的匹配系数,表明这3台发动机均为正常机,与实际情况相符。同理,由表2也可得出类似的相应结论。
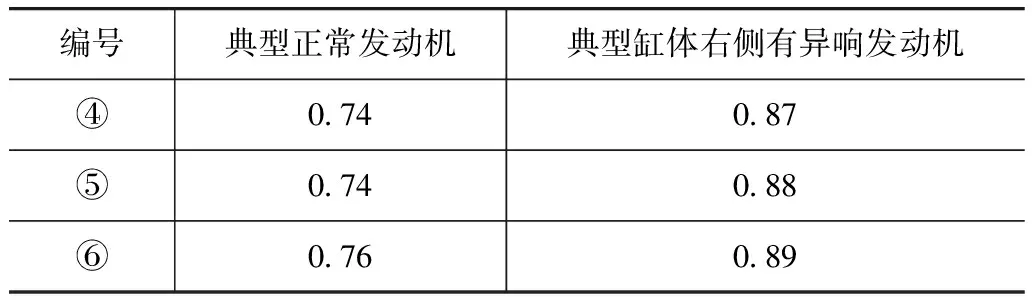
表2 3台缸体右侧有异响发动机与两种典型发动机的匹配系数
5 结论
(1) 由于发动机声信号周期性较强而背景噪声又具有随机性的特点,采用LMS算法降噪,能有效去除该种信号的干扰噪声,提高信噪比,还原信号特征。
(2) SDP图形利用极坐标和图形的对称性特点,能够更加直观有效地对信号进行描述,应用在发动机声信号上也有较好的效果。
(3) LMS算法与SDP图形相结合,能很好地判断发动机是否产生异响,它提供了一种发动机在线异响诊断的新路径。
[1] 杨诚,王中方,杨振冬,等.摩托车发动机缸头异响的监测方法研究[J].噪声与振动控制,2010(4):85-88.
[2] 杨诚,冯焘,王中方,等.基于SDP法诊断发动机的异响[J].声学技术,2010(5):523-527.
[3] 曹亚丽.自适应滤波器中LMS算法的应用[J].仪器仪表学报,2005(S2).
[4] Mahjoob M J, Zamanian A. Vibration Signature Analysis for Engine Condition Monitoring and Diagnosis[C]. In Proceedings of ISMA,2006:18-20.
[5] Pickover C A. On the Use of Symmetrized Dot Patterns for the Visual Characterization of Speech Waveforms and Other Sampled Data[J]. The Journal of the Acoustical Society of America,1986,80.
[6] Widrow B, Hoff JR M E. Adaptive Switchine Circuits[C]. Ire Wescon Conv. Rec. Pt.4,1960,New York:96-104.
[7] Wiener N Hopf E. On a Class of Singular Integral Equations[C]. Proc. Prussian Acad. Math-Phys. Ser. 1931:696-697.
[8] Farhang-Boroujeny B. Adaptive Filters:Theory and Applications[M]. New York, Wiley,1998.
[9] Haykin S. Adaptive Filter Theory[M]. 4th edition. Upper Saddle River, NJ,Prentice Hall, 2002.
[10] Sayed A H. Fundamentals of Adaptive Filtering[M]. New York, Wiley, NJ,2003.
[11] Pickover C. Symmetrized Rand-dot Patterns[R]. IBM Research Report,1983,RC10256.
[12] Katsuhiko Shibata, Atsushi Takahashi, Takuya Shirai. Fault Diagnosis of Rotating Machinery Through Visualisation of Sound Signals[J]. Mechanical Systems and Signal Processing,2000,14(2):229-241.
[13] Rafael C Gonzalez, Richard E Woods. Digital Image Processing(2nd Edition)[M]. Prentice Hall,2002.

