基于SORA方法的汽车耐撞性优化*

陈吉清,郑炳杰,兰凤崇,马芳武

(1.华南理工大学机械与汽车工程学院,广州 510640; 2.华南理工大学，广东省汽车工程重点实验室，广州 510640;3.浙江吉利汽车研究院,杭州 311228)

前言

汽车的碰撞分析是一个复杂的工程技术，在实际工程中由于材料性质、制造工艺和结构外部环境的复杂性以及人为假定等因素的存在，使设计过程中需要考虑的参数存在很大的不确定性，因此在研究碰撞问题的确定性设计的同时，也有必要关注其结构可靠性，降低目标对设计变量的灵敏性[1]。

传统的可靠性优化方法往往是将可靠性约束转化成确定性约束，利用某种算法寻优，最后采用蒙特卡罗法进行可靠性分析，评估优化效果。这种双循环策略的缺点是计算成本高，为改善可靠性分析的计算效率，文献[2]和文献[3]中提出了序列优化与可靠性评估(SORA)方法，这种方法将可靠性分析与确定性优化分开，依次进行，通过在循环迭代中修正约束的方法逼近可靠性解。由于SORA方法的单循环策略明显改善了优化效率，该算法在某些领域已经得到了广泛应用，包括飞航导弹和飞机设计等复杂工程问题[4-8]。

本文中将SORA方法引入到汽车前端碰撞的可靠性分析中，同时借助Kriging[9-10]插值技术，建立了碰撞响应的Kriging代理模型，对汽车前端进行轻量化优化，得到符合可靠性设计的优化结果，有效地提高了计算效率和精度。

1 序列优化与可靠性评估

一般可靠性优化设计模型可描述为

(1)

式中：F(·)表示目标函数；d为确定性设计变量；x为随机变量；Pr为满足括号内边界条件的概率；G(·)为约束条件函数；R为要求达到的可靠度。

传统的可靠性优化方法将任意分布参数的可靠性约束等价转化为

G+βσg≥0

(2)

式中：β为可靠度R对应的可靠性指标；σg为响应的方差。

该优化过程须要计算响应的均值、方差和随机约束的概率，以评估响应的可靠性，常用的方法有蒙特卡罗法[1]、一次二阶矩法[11]等。它是一个双循环策略，其外部循环是确定性优化，内部的可靠性分析嵌套在优化循环中，每次迭代皆须进行完整的可靠性分析，计算效率低。为弥补这一缺陷，文献[2]中提出了一种单循环策略的SORA方法，它将可靠性分析和确定性优化分离，用上一次可靠性的分析结果来修改下一次确定性优化的约束条件，这样大大提高了可靠性分析的效率。

一个包含两个随机设计变量的优化模型为

(3)

式中：μx为随机变量的均值，μx=(μx1,μx2)。

状态函数为

G(x1,x2)=0

(4)

假设x1和x2为相互独立的正态分布变量，现对其进行当量标准正态化变换：

x=(x-μx)/σx

(5)

式中：σx表示随机变量的标准差，σx=(σx1,σx2)。

定义可靠性指标为

(6)

则可靠度可表示为

R=φ(β)

(7)

将式(5)代入式(4)可得到在标准正态分布空间的约束界面，如图1所示，进一步求解式(3)中的目标函数F(·)的最小值，即能在界面上搜索到设计验算点MPP。点(μ1,μ2)就是该约束条件下的确定性分析的最优解。

如图1所示，MPP处的正态分布曲线表示变量的概率分布密度，可见确定性分析的可靠度大约为50%，对于可靠性分析来说，其可靠度太低。由设计要求的可靠度R，可得到概率性失效点MPPi，它即为变量可行性区域的边界点。为达到可行性要求，变量的可行性区域应该全部落在确定性边界以内。因此须进行约束修正，约束的移动距离用s表示。此时的确定性约束修正为

G(μx1-s1,μx2-s2)≥0

(8)

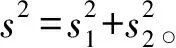
于是，第k次循环的优化模型可表示为

(9)

每一次循环的可靠性相对上一次循环得到了改善，若可靠性仍达不到设计要求，则继续修正约束条件，直到计算收敛，其流程如图2所示。以此类推，多个变量的优化模型也能通过同样的序列化循环方法，在较短的时间内求解得到可靠性结果。SORA方法相对于传统可靠性优化的优势在于，采用单循环策略很好地集成了可靠性分析和确定性优化，并且在进行可靠性分析时，将前一轮循环得到的最优解，作为下一轮循环中优化的初始点，前一轮循环得到的逆MPP，作为下一轮循环中搜索逆MPP时的初始位置，减少可靠性分析的次数，提高优化效率。

2 汽车耐撞性仿真模型与代理模型

2.1 仿真模型与试验设计

图3为汽车前端的数值模型，包括整车模型中发动机舱防火墙以前的部分，后面部分由于在碰撞过程中变形较小，对分析前防撞系统的耐撞性影响较小，用一个集中质量单元代替。模型被截断处的节点定义为节点集，通过RBE单元与质量单元连接起来。质量单元处施加了一个运动约束，约束曲线为整车碰撞的B柱下方输出频率为1 000Hz的位移-时间曲线。这样就确保了该模型的总质量和运动状态与整车模型保持一致。该有限元模型包含184 991个节点，192 035个单元，其中三角形单元个数为8 711，占总单元数的4.5%，符合三角形单元不超过5%的精度要求。单元之间无穿透、干涉现象存在。

在构造代理模型的过程中，试验点的选取非常重要，良好分布的试验点有利于更加精确地反映响应和设计变量之间的关系[12]。相反，不具有代表性的试验点则可能导致所构造的模型失真。本文中采用拉丁超立方抽样方法，通过控制抽样点的位置，避免出现小邻域内被多次抽样，且无被忽略区域。若进行n次抽样，把m个随机变量分别等分为n个区间，则整个抽样空间就被划分成n个m维区间。对于每个变量，保证n次随机抽样一定分别落在各小区间，因此抽样点被等概率地分布到整个随机空间内。

运用拉丁超立方抽样方法选取了20组样本点，各方案的试验结果见表1。其中方案0表示优化前的状态；T1～T5为设计变量，如图4所示，分别表示前横梁、吸能盒内、外板和前纵梁内、外板的板厚；M为被优化零件的总质量；E为碰撞过程中吸收的总内能。

表1 拉丁超立方试验设计表

2.2 建立Kriging代理模型

Kriging方法是一种无偏插值方法[13-14]。Kriging近似模型假设系统的响应由一个参数模型和一个非参数随机过程联合构成：

y(x)=F(x)+Z(x)

(10)

式中：F(x)为参数模型，为多项式回归方程；Z(x)为随机分布，提供对模型局部偏差的估计，具有以下特性：

E[Z(x)]=0

(11)

(12)

(13)

式中：xi和xj表示样本点中的任意两个点；R(θ,xi,xj)为带参数θ的相关函数。

任意一个待测点xn通过已知的抽样点来预测，用抽样点的响应矩阵Y的线性组合表示为

(14)

Kriging的无偏特性要求预测误差的均值为零，并且预测方差应最小化，于是综上所述能求得系数矩阵c。HyperWorks软件中的HyperKriging工具箱集成了上述代理模型的构建程序，通过调用该程序可计算得到Kriging近似模型。

半参数化的Kriging模型无须建立一个特定的数学模型[9]，相对于参数化模型而言，Kriging模型的应用更加灵活和方便。图5为经典数学函数“墨西哥帽子”的各种拟合试验，“墨西哥帽子”的解析方程式为

z=sinr/r

(15)

图5(a)为式(15)用Matlab软件模拟的解析解；图5(b)为运用Kriging方法通过20个抽样点插值构造的模拟解；图5(c)为用二次响应面构造的模拟解，采用的抽样点与图5(b)相同。通过这个简单的非线性算例，可以看出Kriging方法对高非线性问题的模拟精度和整体适应性优于二次响应面方法。

将试验数据导入HyperWorks，通过以上求解程序求得吸能量E的Kriging响应模型。直观上可以预见板件的质量与板厚的函数关系为线性关系，因此采用最小二乘法对试验数据进行线性拟合，即得到总质量M与设计变量T之间的函数关系为

M=1.98T1+0.38T2+0.69T3+3.02T4+1.79T5

(16)

3 SORA优化与验证

3.1 SORA优化

本算例的优化目标是：在轻量化的同时要求吸能效果最佳。为达到轻量化目标，制定以下约束：对吸能部件总质量进行约束，要求其至少能减质量1kg，同时希望碰撞过程吸收的内能最大，即减质量对吸能的削弱影响最小。优化问题用以下数学模型描述为

(17)

假设板厚T为服从正态分布的随机变量，令其方差为0.006，要求约束满足可靠度为95%，将设计目标和约束条件代入图2的SORA流程进行计算，经过3次迭代达到收敛，迭代过程如表2所示。其中可靠性边界解表示正态分布变量对应的目标解集中，发生概率为Pr=1-R处的边界解。第1次确定性优化所得到的解一般不满足设定的可靠性条件，这一步得到的目标解M刚好落在约束边界，但可靠性边界解不符合约束条件，因此通过寻找逆MPP点，确定s的值，对约束进行修正进入第2次迭代。经过第2次优化后，M的目标解往可行区域内移动，可靠性得到改善，但可靠性边界解仍不符合要求，即没有达到可靠度为95%的要求，需进一步修正约束。第3次迭代后，M的可靠性边界解落在可行区域内，计算收敛。

表2 迭代过程

文献[1]中采用了传统的可靠性优化方法，在进行了确定性优化后，采用蒙特卡罗法抽取了100组设计变量对优化结果进行可靠性评估，若评估结果符合要求，计算终止；若评估结果不符合要求，须返回到整个优化流程的第一步，重新进行确定性优化和可靠性评估。本文中采用SORA方法，仅进行了3次约束修正即完成了可靠性优化过程，其计算成本相对传统可靠性优化明显降低。

3.2 结果验证

经过SORA优化后的设计变量如表3所示。将其预测值与有限元仿真的试验值进行对比验证，结果如表4所示。

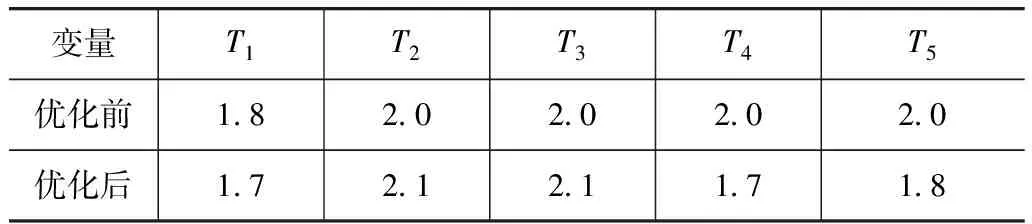
表3 设计变量优化结果 mm

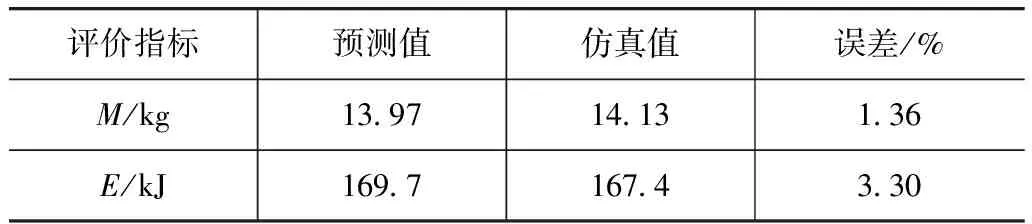
表4 预测结果验证

从表4可以看出，质量M的相对误差很小，这是因为质量与板厚是线性关系，用最小二乘法拟合能精确拟合线性问题。Kriging模型拟合的吸能量E也达到了很高的精度，可以认为采用的代理模型有效。从优化结果看，吸能部件的质量从15.56kg下降到14.13kg，减质量1.43kg，达到了优化目标；优化后的吸能量为167.4kJ，相对原模型提高了0.3kJ，达到了预期目标，即减质量对吸能效果影响最小。以上结果表明，Kriging结合SORA的优化方法有效。

为验证结果的可靠性，采用蒙特卡罗描述性抽样获得1 000组设计变量，将1 000组设计变量分别代入代理模型中计算响应的均值和方差，判断约束的失效概率。图6给出了质量M和吸能量E的频数直方图。

如图6所示，试验结果大致呈正态分布。质量M大于14.5kg的试验次数为44次，即失效概率为4.4%，符合可靠度为95%的要求。同时，质量M和吸能量E试验值的均方差值Dev相比其均值非常小，表明试验数据偏离均值的程度很小，优化结果的响应对该设计点自变量的敏感度不高，该优化设计具有较高的鲁棒性。综上所述，本文中采用的优化方法具有较高的精度，并且优化结果符合可靠性要求。

4 结论

(1) 将SORA方法引入到汽车耐撞性的可靠性优化，通过理论分析和实例分析，验证表明SORA方法可以有效地处理耐撞性优化问题。

(2) 通过与传统双循环优化策略的对比，表明SORA方法在处理可靠性优化问题时更高效。

(3) SORA方法的关键在于不断修正约束去逼近可靠性约束，当目标函数与约束条件的非线性程度太高或者出现不连续时，约束的修正和确定性优化会影响可靠性指标的收敛。本文中构造了Kriging代理模型，避免了原模型的复杂性，保证了迭代的收敛，同时具有较高的模拟精度。

[1] 谢然,兰凤崇,陈吉清,等.满足可靠性要求的轻量化车身结构多目标优化方法[J].机械工程学报,2011,47(4):117-124.

[2] Du X, Chen W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design[J]. Journal of Mechanical Design,2004,126(2):225-233.

[3] Yin X, Chen W. Enhanced Sequential Optimization and Reliability Assessment Method[J]. Structure and Infrastructure Engineering,2006,2(3):261-275.

[4] 夏青,蔡洪,张士峰.可靠性优化方法在飞航导弹多学科设计优化中的引用[J].弹箭与制导学报,2010,30(1):40-42.

[5] 王宇.基于不确定性的优化方法及其在飞机设计中的应用[D].南京:南京航空航天大学,2010.4.

[6] 黄洪钟,余辉,袁亚辉,等.基于单学科可行法的多学科可靠性设计优化[J].航空学报,2009,30(10):1871-1876.

[7] 陈仁伍,谷良贤,龚春林.一种基于SORA方法的多学科可靠性设计方法[J].机械强度,2008,30(1):37-40.

[8] 余辉.基于协同优化和单学科可行法的可靠性优化设计[D].成都:电子科技大学,2008.6.

[9] 高云凯,孙芳,余海燕.基于Kriging模型的车身耐撞性优化设计[J].汽车工程,2010,32(1):17-21.

[10] 王国春,成艾国,胡朝辉,等.基于Kriging模型的汽车前部结构的耐撞性优化[J].汽车工程,2011,33(3):208-212.

[11] 孟广伟,赵云亮,李锋,等.含多裂纹结构的断裂可靠性分析[J].吉林大学学报(工学版),2008,38(3):614-618.

[12] 张建国,苏多,刘英卫.机械产品可靠性分析与优化[M].北京:电子工业出版社,2008:109-115.

[13] Sakata S, Ashida F, Zako M. Structural Optimization Using Kriging Approximation[J]. Computer Methods in Applied Mechanics and Engineering,2003,192:923-939.

[14] 高月华.基于Kriging代理模型的优化设计方法及其在注塑成型中的应用[D].大连:大连理工大学,2009,4.