基于微粒群算法的PID控制器优化研究

宋莉莉朱 超孙万麟

（1，2，3.昌吉学院物理系 新疆 昌吉 831100）

基于微粒群算法的PID控制器优化研究

宋莉莉1朱 超2孙万麟3

（1，2，3.昌吉学院物理系 新疆 昌吉 831100）

微粒群算法是近年来提出的一种新型群体智能优化算法，它具有结构简单，收敛速度快，所需参数少等优点.为改善传统PID参数整定问题，提出了基于微粒群算法整定PID控制器参数的优化设计方法.通过对双容水箱建模并与传统整定方法进行仿真比较.仿真结果表明，采用微粒群算法来优化PID参数，可以获得综合性能良好的PID控制器参数.对控制器的设计具有一定的指导意义.

微粒群算法；PID控制；参数整定；优化

1 引言

PID控制器自产生以来，一直是工业生产过程中应用最广也最成熟的控制器.PID控制器参数整定的合适与否对控制器性能有重要影响.常用的PID控制器参数整定方法主要是工程整定法如Ziegler-Nichol法.在工业控制中，大多数控制对象是高阶、非线性的，这些传统的方法难以实现对参数的优化整定，易产生振荡和大的超调.为了解决这一问题，近几年来，提出了许多基于人工智能技术的PID参数整定方法，如单纯形法［1］、模拟退火算法［2］［3］、遗传算法［4］等，但是遗传算法在编码和解码过程中占用内存时间较大，易早熟收敛陷入局部最优，不能得到很好的整定效果.

微粒群(PSO)算法由于其思想简单，需要调整的参数少，程序易实现，在科学计算和工程应用领域已被广泛应用.本文是基于微粒群算法的PID参数优化问题，利用微粒群算法良好的寻优能力，结合MATLAB强大的Simulink系统仿真功能,并通过与常规PID参数整定方法比较，证明了微粒群算法的有效性，使系统得到良好的控制效果。

2 PID控制器工作原理

PID控制即比例(P)、积分(I)、微分(D)控制器，它是一种线性控制，其作用是将给定值r(t)与被控参数的实际输出y(t)之差e(t)=r(t)-y(t)作为控制器的输入，控制器按偏差的比例、比例加积分、比例加积分加微分形成控制量.将三种运算结果相加，就得到PID控制器的输出.在连续时间域中，PID控制器算法的表达式为：

PID控制器的参数整定,就是在系统控制的快速性与稳定性之间进行折衷.尽量减小超调量和稳态误差，提高动态响应速度［5］.

3 基本微粒群优化算法及改进

粒子群优化算法（Particle Swarm Optimization,PSO）是1995年由美国的心理学家James Kennedy和电气工程师Russell Eberhant在鸟群的行为规律启发下共同提出的.它是将每只鸟抽象为一个个没有体积没有质量的粒子，在搜索空间中以一定的速度飞行，粒子根据它本身的飞行经验和同伴的飞行经验

来动态调整.在每一代中，粒子将跟踪两个极值：一个是粒子本身迄今为止找到的最优解，另一个是整个群体迄今为止找到的最优解［6］.

假设一个由M个粒子组成的群体在D维的搜索空间以一定的速度飞行.第i（1≤i≤M）个微粒在第d（1≤d≤D）维的位置、速度分别为：

PSO算法具有深刻的群体智能背景，在多维空间寻优、动态目标寻优等方面有着收敛速度快等优点.由于PSO算法在优化过程中所有粒子都向最优解的方向飞去,所以粒子趋向同一化,群体的多样性逐渐丧失,致使后期算法的收敛速度明显变慢,甚至处于停滞状态,故难以获得较好的优化结果.为了克服这一缺点,1998年，Y.Shi［7］等提出带有惯性权重的粒子群算法.惯性权重w的大小决定了粒子对当前速度继承的多少，选择一个合适的w有助于微粒群算法均衡它的探索能力与开发能力.若w较大，则有利于展开全局寻优；若w较小，则有利于局部寻优.为了保证微粒群算法在开始时具有良好的全局搜索能力，在后期具有良好的局部搜索能力，从而精确的得到全局最优解，故在迭代计算过程中，让惯性权重w呈线性递减.其位置公式保持不变，速度公式为：

公式（4）中，c1、c2为加速因子，r1、r2为分布在(0,1)之间的随机数,w称为惯性权重.此外，为使粒子速度不致过大，可设定速度上限vmax，即当vid＞vmax时，取vid=vmax；当vid＜-vmax时，取vid=-vmax.它主要由三部分组成：第一部分为微粒先前行为的惯性，表示粒子对当前自身运动状态的信任，依据自身的速度进行惯性运动；第二部分为“认知”部分，表示微粒本身的思考；即综合考虑自身以往的经历从而实现对下一步行为决策.它反映的是一个增强学习的过程；第三部分为“社会(social)”部分，表示微粒间的信息共享与相互合作［8］.选择一个合适的w有助于微粒群算法均衡它的搜索能力.Y.Shi［9］等研究发现，让惯性权重w从0.9线性递减到0.4的策略可以提高算法的收敛速度和全局搜索能力.

4 基于PSO算法的PID控制器优化设计

4.1 PSO-PID控制器结构图

PID参数整定就是选择合适的3个参数得到性能良好的PID控制器.从优化的角度来说，就是从这3个参数组成的3维搜索空间中寻找一组最优的参数使PID控制器的效果达到最优.其结构图如图1所示：

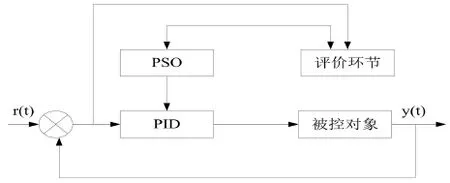
图1 PSO-PID控制器结构图

PID控制器的三个参数分别为比例(kp)、积分(ki)、微分(kd)系数.kp可用来加快系统的响应速度,调

节系统的精度,优化系统动态和静态的特性；ki主要是用来消除系统的稳态误差；kd主要是用来改善系统的动态特性.这三个参数都直接影响PID控制器的控制效果,如果其中一个值过大或过小,都对其它两个值有影响,不能得到期望的控制器.所以要想取得理想的控制效果,达到控制要求，就要对这三个参数进行调整和优化.

4.2 参数的编码

设种群中的粒子数为M,每个粒子的位置矢量由PID控制器的三个控制参数组成即粒子矢量的维数D=3.该矩阵可以表示为：

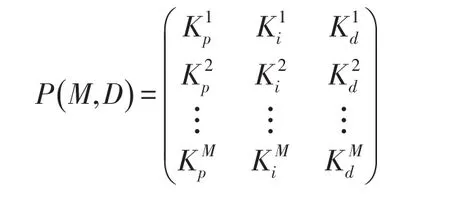
4.3 适应度函数选取

由于PID参数优化是求目标函数的极小值问题，为了获取满意的静态性能和动态性能，使系统能够得到快速、平稳、超调小的控制效果.由于PID参数优化是求目标函数的极小值问题，根据控制性能的要求，本文采用误差绝对值乘时间积分的性能指标作为参数选择的目标函数.

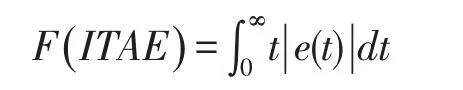
4.4 PSO算法整定PID参数的流程图

PID控制器的优化设计可视为一个多目标的优化问题.常规的PID参数整定方法很难同时兼顾多项指标,得到的PID控制器通常不是最优的.利用PSO的全局搜索和多目标优化能力,可获得综合性能良好的PID控制器,从而克服传统整定方法的缺点.其流程图如图2所示：

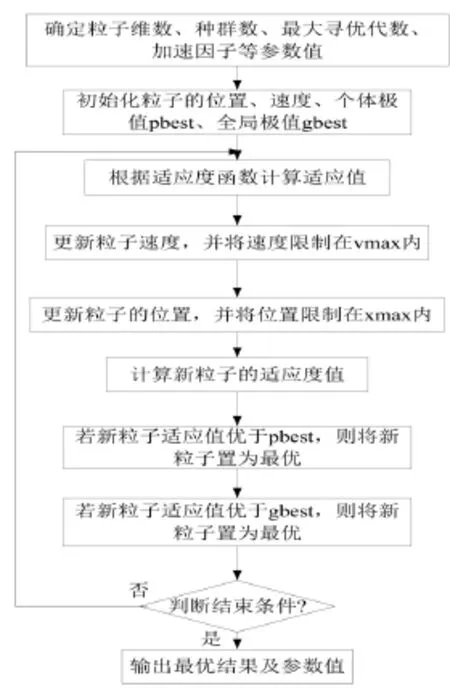
图2 粒子群算法流程图

4.5 PSO算法整定PID控制器参数的源程序编码

5 仿真建模及分析

为了验证PSO算法对PID参数进行优化设计方法的有效性，假设有两只水箱串联工作设被控量是第二只水箱的液位h2，输入量为q1根据物料平衡关系可列出下列方组：

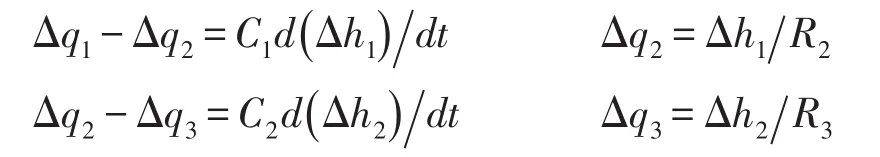
上述方程组进行拉氏变换得：

将上述公式可得双容过称模型：

图3 双容过程框图

根据框图可得双容过程的数学模型为：

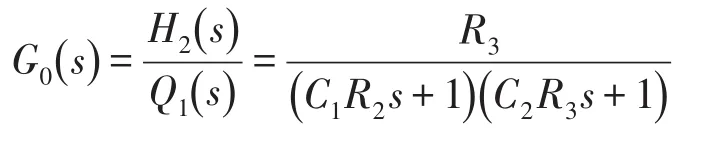
令：K0=R3；T1=R2C1；T2=R3C2

则双容过程的数学模型：

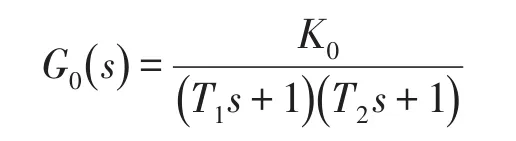
式中K0为过程的放大系数；T1为第一只水箱的时间常数；T2为第二只水箱的时间常数；C1、C2分别

为两只水箱的容量系数。

K0=6.27；T1=751；T2=12.96可得过程的传递函数［10］：

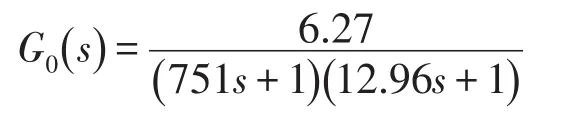
按前面所述的方法，对该系统所选参数为：种群维数为3，种群数为30，迭代次数为30，评价指标：

采用传统方法进行PID参数调整可得常规PID控制的参数分别为：Kp=12.4 Ki=0.62 Kd=82.31

根据PSO算法的优化算法分析，可以得到系统最优的PID参数分别为：Kp=14.17 Ki=0.022 Kd= 7.34

将两种方法进行仿真可以得到如图4所示的结果

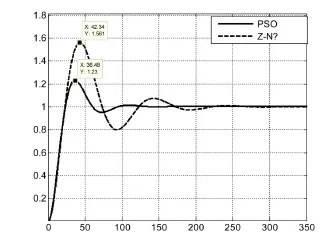
图4 系统的单位阶跃响应曲线

从仿真的结果可以看出，与Z-N法比较，系统闭环控制的超调量、调节时间等指标都得到不同程度的改善。另外，利用PSO算法得到的虽然传统PID控制初次达到稳定值的时间比PSO-PID的时间要短，即上升速度要快，但是其并没有稳定下来，此后要需要较长的时间调整，其调整时间比PSO-PID控制要长.因此，利用PSO算法得到的PID控制器优于常规方法整定PID的控制器.

6 结论

本文针对PSO算法具有良好的搜索能力和收敛速度，提出了基于PSO算法的PID参数优化设计方法.并用微粒群算法与传统PID整定方法对双容水箱数学模型进行仿真实验对比，结果表明，利用微粒群算法整定PID参数可以得到良好的控制效果.

［1］蒋珉.控制系统计算机仿真［M］.北京:电子工业出版社,2006.

［2］黄友锐,曲立国.PID控制器参数整定与实现［M］.北京:科学出版社,2010.

［3］李丽,牛奔.粒子群优化算法［M］.北京:冶金工业出版社,2009.

［4］蔡自兴.智能控制导论［M］.北京:中国水利水电出版社,2007.

［5］吴启迪,汪镭.智能微粒群算法研究应用［M］.江苏:江苏教育出版社,2005.

［6］王静,蒋珉.若干优化算法的运行分析比较［J］.计算机仿真2006,23(3):150-153.

［7］邵裕森,戴先中.过程控制工程［M］.北京:机械工业出版社,2000.

［8］陶永华.新型PID控制及其应用［M］.北京:机械工业出版社,2002.

［9］王凌,刘波.微粒群优化与调度算法（Particle Swarm Optimization and Scheduling Algorithms）［M］.北京:清华大学出版社,2008.

［10］刘建军.基于寿命的粒子群算法研究［J］.计算机应用与软件，2011,28(6):157-160.

TP301.6

A

1671-6469（2014）06-0076-05

2014-09-15

昌吉学院研究生启动基金“粒子群算法研究及应用”（2014SSQD003）

宋莉莉（1987—），女，昌吉学院物理系，研究方向：智能控制与系统开发。