克拉默法则的几何直观教学探讨

王秋平郑瑞楠

（1.昌吉学院数学系 新疆 昌吉 831100；2.新疆农业职业技术学院工程学院 新疆 昌吉 831100）

克拉默法则的几何直观教学探讨

王秋平1郑瑞楠2

（1.昌吉学院数学系 新疆 昌吉 831100；2.新疆农业职业技术学院工程学院 新疆 昌吉 831100）

本文从向量的观点来看线性方程组，使其具有直观的几何意义，再借助二维图直观轻松地得到二元方程组的克拉默法则，并将之推广到n维的情形，不仅使得克拉默法则具有几何直观的背景，而且使克拉默法则易学易懂。

线性方程组；克拉默法则；几何直观教学

1 引 言

解线性方程组是线性代数中主要的任务之一[1-2]，而克拉默法则是解决方程组的个数和自变量个数相同的线性方程组的解的问题。但是由于其抽象性，往往让学生很难轻松的学习和掌握。笛卡尔曾说：“没有任何东西比几何图形更容易印入脑际了，因此用这种方式来表达事物是非常有意义的。”显然，几何直观教学对数学教学意义重大，尤其是线性代数极为显著。因此在线性代数的教学中应对一些定义定理给出适当的几何解释和几何图形，配合计算和推导，能够使学生轻松而迅速的理解掌握线性代数的基本概念和几何本质，建立感性认识，从而具备理解复杂和抽象数学的能力。近几年的线性代数课程改革中，有很多文献中也提到了几何直观教学的重要性，如文献[3]给出了行列式、正交变换、线性方程组与直线、平面的位置关系的几何解释；文献[4]中指出以行列式和二次型为例，讲解低维的几何解释进而推出高维的几何解释，从而激发学生的学习兴趣；文献[5]则是从行列式的几何意义入手，通过几何直观引出克拉默法则的代数证明过程，而本文试图从向量的观点重新审视线性方程组，使其具有直观的几何意义，再借助二维图直观轻松地得到二元方程组的克拉默法则，并将之推广到n维的情形。

2 克拉默法则的几何直观教学

下面以求解方程组为例，说明如何通过向量的观点来看行列式、线性方程组，使得原本解决线性方程组的问题有了直观的几何意义，从而让学生在直观背景下更好的理解克拉默法则。为了更直观的表达向量，在此仅以二阶线性方程组为例来说明，高阶的线性方程组可以自然类推。假设有二阶线性方程组，

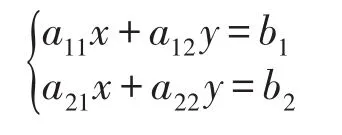
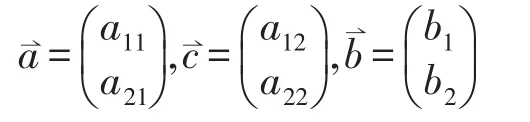
则上述方程组可以表示为：

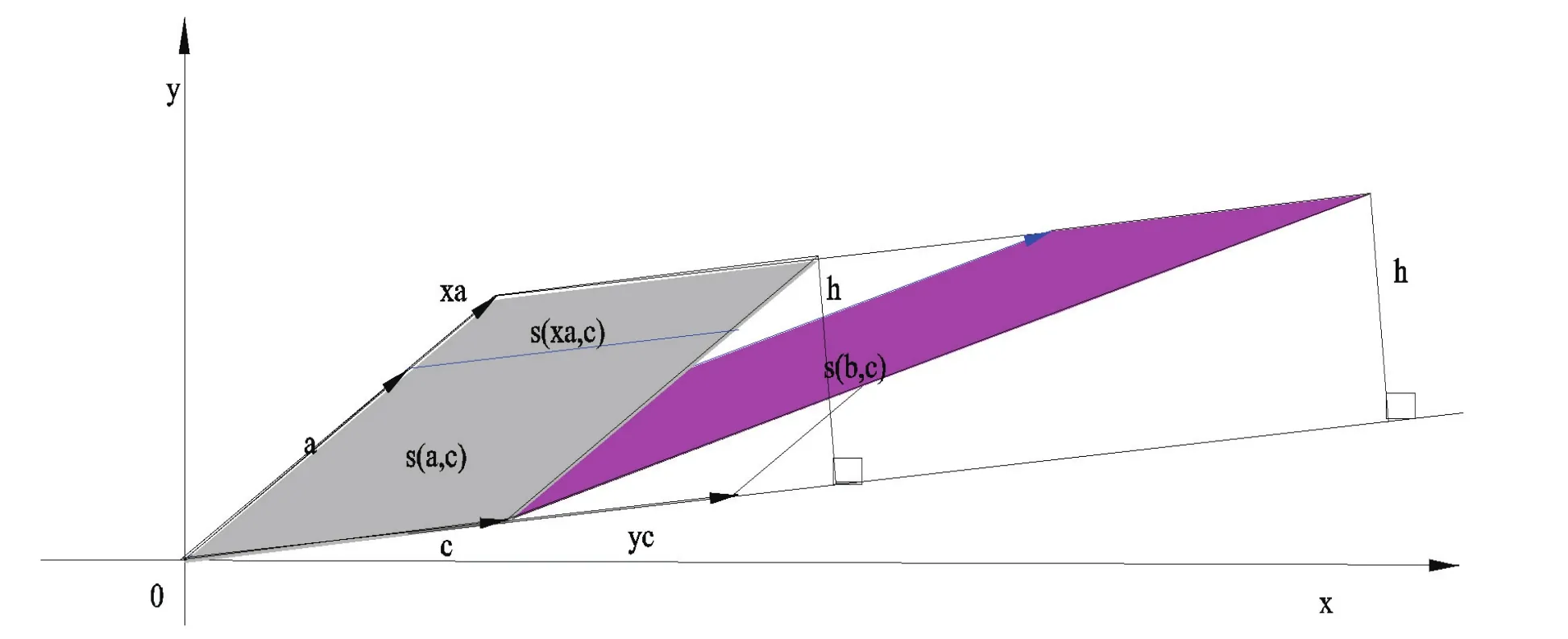
首先，由向量混合积几何意义及行列式的几何意义表示可知，向量构成的平行四边形的面积可以表示为或者，向量构成的平行四边形的面积可以表示为或者向量构成的平行四边形的面积可以表示为或者

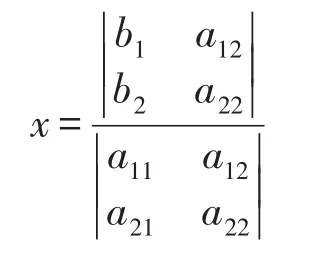
同理，可得

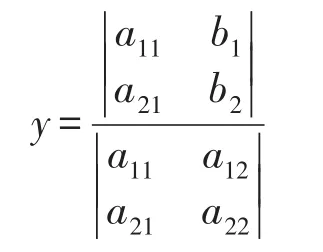
把抽象的数学问题转变为具有几何直观的问题，更容易理解。

同时在此过程中，我们对向量的变化仅仅是伸缩、旋转和切变等，只是对向量的大小和方向改变，没有对向量进行弯曲和扭曲变化，从而更加加深学生理解线性变化的本质含义。

我们可以进一步推广，当线性方程组的未知数为3个时，由克拉默法则所得解的几何意义是相应六面体的体积比；当线性方程组未知数的个数推广到n个时，由克拉默法则所得解的几何意义则是相应平行多面体的体积比。

3 结束语

通过上述几何方法推导出克拉默法则，学生就容易理解并掌握克拉默法则，也激发了学生的学习兴趣。当代数学家徐利治曾说：“无论从事数学教学或研究，我是喜欢直观的。学习一条定理及其证明，当我能把定理的直观含义和证明的直观思路弄明白了，我才认为真正懂了。”几何图形就具有这样的作用，它以生动的形象将抽象的东西具体化，给人以直观感受，所以对于理论深刻、内容零散且计算复杂的线性代数课程来说，几何直观教学相当重要，值得每一位线性代数教师去挖掘和实现这种教学手段。

［1］同济大学数学教研室.线性代数［M］.北京:高等教育出版社,2009:1-155.

［2］David C.Lay,Linear Algebra and Its Application（Third Edition）［M］.New Jersey:Addison-Wesley,Pearson Education, Inc.,2006:1-586.

［3］章晓.线性代数与解析几何结合教学探析［J］.山东师范大学学报,2008,23（3）:132-133.

［4］陈建华,蔡传仁.几何直观在线性代数教学中的应用［J］.工科数学,2002,18（1）:87-90.

［5］谢琳,张静.从几何直观理解行列式与Cramer法则［J］.高等数学研究,2009,12（1）:61-62.

O151.1;G642.1

A

1671-6469（2014）06-0065-03

2014-04-16

王秋平（1986—），女，吉林榆树人，昌吉学院数学系，研究方向：高等数学及贝叶斯统计。