水中电火花放电能量分配系数研究

高睿恒，张发旺，顾 琳，赵万生

（上海交通大学机械与动力工程学院机械系统与振动国家重点实验室，上海200240）

水中电火花放电能量分配系数研究

高睿恒，张发旺，顾 琳，赵万生

（上海交通大学机械与动力工程学院机械系统与振动国家重点实验室，上海200240）

采用实验与仿真相结合的方法，通过设计不同的峰值电流及脉宽等加工参数，对水中电火花加工的能量分配系数及电蚀坑形貌的形成进行了研究。基于COMSOL MULTIPHSICS仿真软件建立固体-流体传热耦合模型。通过试验得到不同峰值电流及脉宽条件下的电蚀坑半径，结合最小二乘法拟合电蚀坑半径与脉宽、电流之间的关系。利用拟合公式和所建模型，在不同加工参数下得到不同能量分配系数对应的电蚀坑尺寸。通过与试验测量结果进行比对得到水中电火花放电的能量分配系数，并验证所建模型的正确性。

水中电火花放电；能量分配系数；固体-流体传热耦合模型

电火花加工是以热能蚀除材料的一种特种加工方法，属于非接触式加工，具有许多传统切削加工无法比拟的优点 （如加工能力与材料硬度无关、无宏观加工效力），在模具、航空、宇航、电子、精密机械、仪器仪表、汽车等行业得到广泛的应用，在制造复杂形状的工件方面具有独特的优势。在电火花加工过程中，由于放电能量通常分配消耗在工具电极、加工工件及工作电介质周围，所以分配到工具电极和工件表面的能量是去除材料和影响工件表面质量的直接原因。而材料去除率和加工表面质量是影响电蚀坑形貌的主要因素，因此，分析电火花加工的能量分配系数，不但能预测材料去除率和加工表面质量，而且能进一步验证电蚀坑尺寸与热能之间的关系，并能得到等离子体半径的最高温度。

近年来，国内外学者对工作液中电火花放电加工的能量分配系数及放电机理等方面进行了研究。夏恒等[1]通过测量放电加工形成的电蚀坑体积与电极材料温升，并结合有限差分理论计算，得到油基工作液中铜铜电极对正负极能量分配系数分别约0.45和0.25；但其研究对于测量温度的设备精度要求极高，且如果在加工过程中对工具电极有摇动或

高速旋转等工艺要求时，则对于测量设备和试验设计将具有更高的要求，以至于不能直接观测。DiBitonto等[2]经试验研究得到传统电火花加工中负极与正极的能量分配系数分别约0.183和0.08，且该结果在电火花加工热物理模型的研究中被广泛引用[3]；但其研究需进行大量的计算和实验，才能求解根据能量分配系数的传热方程。Ikai等[4]设计了不同加工参数的放电加工实验，并以实验结果拟合了所形成的电蚀坑半径随时间、电流变化的半经验公式，该公式成为分析和模拟电火花加工的普遍公式；但其研究与水中电火花加工不同，所以等离子体通道半径的半经验公式不再适用于水中电火花加工。薛荣等[5]通过实验与仿真分析相结合的方法，建立了热-流耦合模型，分析并确定了阴阳极的能量分配系数分别为0.29和0.025，并得到了传热温度分布与电蚀坑的形貌。然而，水中电火花加工的电介质具有不可压缩性，密度和介电系数与雾中电火花加工的特点有明显不同，且等离子体通道内的能量密度更高，因此，雾中热-流耦合模型不再适用于水中电火花加工。

此外，关于雾中电火花加工能量分配系数及电蚀坑形成机理等方面的研究很多，但关于水中电火花加工能量分配系数及放电机理的研究却很少，且水中电火花加工的水介质相对静止及仅涉及固体和流体传热两种形式，可降低电火花放电机理的复杂程度，因此，研究水中放电的能量分配系数与放电机理十分必要。本文首先基于Comsol仿真软件，建立固体-流体传热模型，并利用实验得到的电蚀坑半径与多项式拟合传热模型所需的水中电火花放电半径的半经验公式；再在固体-流体传热模型中设定不同的能量分配系数，并以高斯分布为其热源得到相对应的电蚀坑半径，将仿真结果与实验电蚀坑测量值进行对比，得到与实验测量值相符的能量分配系数，并以此验证固体-流体传热模型的正确性；最后，在正确的固体-流体传热模型中计算不同加工参数的电蚀坑半径。由于等离子体通道扩张过程复杂，对于等离子体放电机理的研究并没有被人们完全理解，因此，模拟分析能量分配系数及放电能量与电蚀坑半径之间的关系时，需进行简化假设，这将在后面的章节进行介绍。

1 水中电火花加工机理与传热模型

1.1 水中电火花加工机理

放电加工是利用脉冲放电产生热能来去除材料的，其放电过程总体可分为：极间介质的电离，击穿介质形成放电通道，电极材料受热熔化、气化直至抛出，极间介质的消电离等过程。由于去离子水的密度和介电性能相对气体、雾气和煤油的密度更高，且由于水介质的不可压缩性，使水中放电加工具有与气体、雾中和煤油不同的特点。图1是水中电火花加工装置。

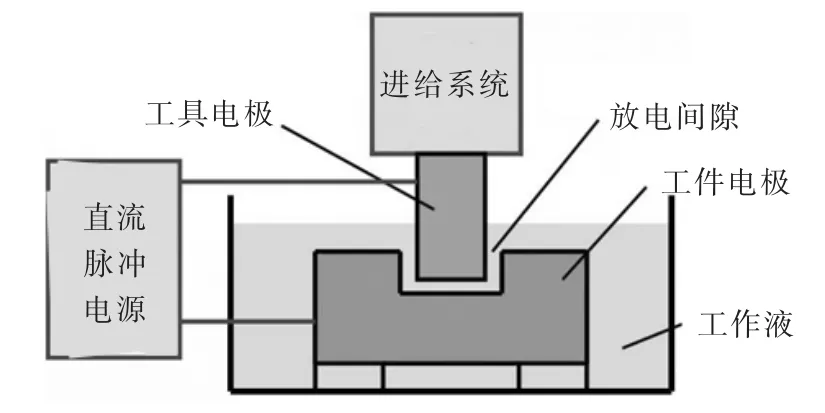
图1 水中电火花加工装置

在水中放电加工的过程中，脉冲电压在电极与工件之间形成极间电场，使电子与水分子之间的撞击不断加快，产生碰撞电离，极间电场之间产生大量正负离子，导致电子雪崩式增加，使极间介质被击穿，从而形成放电通道。带电粒子的动能通过碰撞转变为热能，在工件表面形成热源，是工件材料被蚀除的主因。由于水中电火花加工的等离子体通道中心温度极高，加上去离子水的不可压缩性，限制了放电通道的扩张，因此，水中电火花加工比气中、雾中的扩张半径更小。

1.2 传热模型与假设

由于电火花加工的等离子体通道非常复杂，它是电磁学、热力学、流体动力学等在放电脉冲极短的情况下综合作用的结果，且电火花加工的相关机理也没有被人们完全认识清楚，所以要对水中电火花加工的传热模型进行简化假设：①传热过程主要以热传导和对流传热为主；②等离子体半径与传热半径及电蚀坑半径一致；③ 工件、电极及去离子水都是均质且各项同性的材料；④每次放电只产生一个电蚀坑；⑤ 等离子体放电通道是一个均匀圆柱体；⑥电蚀坑是熔融材料被完全抛出后形成的。

2 正极所分配的能量

峰值电流与放电脉宽是单次放电在正极工件所分配能量的主要影响因素，而能量分配系数所决定的正极能量是电蚀坑形成的主要原因。为了得到不同峰值电流、不同脉宽的电蚀坑形貌，设计的实验加工参数见表1。

表1 加工参数

在表1所示的加工条件下，以紫铜材料、塞尺工具钢分别作为工具电极和工件材料，在电火花成形机床上进行水中电火花加工实验。其中，击穿维持电压在整个放电过程中保持不变，但其数值是固体-流体传热模型分析能量分配系数和电蚀坑形貌的一个重要参数；通过罗氏线圈与Tektronix示波器能测得放电加工的击穿维持电压约为20 V、峰值电流分别为30 A和15 A、脉宽分别为30 μs和60 μs的放电波形（图2）。表2是在表1所示的加工条件下测得的电蚀坑直径与深度尺寸。

表2 不同加工参数时的电蚀坑直径与深度

图2 水中电火花加工的放电波形图

本文的实验数据采用正极性加工得到。由表2可见，随着放电能量的不断增大，工件表面的电蚀坑半径也不断增大。结合最小二乘法拟合工件的电蚀坑半径随峰值电流、放电脉宽变化的规律，可表示为：

式中：I为峰值电流；ton为脉宽。

在分析电火花加工的能量分配系数和放电能量与电蚀坑之间的关系时，通常以高斯分布随时间变化的函数等效为等离子体热源Q(r)[5]：

式中：Q(r)为总热流密度；Q0为加工表面处的最大热流密度；r为几何模型中某点至放电点中心的距离；Rpa为正极等效热量输入半径。

为了准确模拟单次放电在传热区域的温度场分布，由能量分配系数所决定的正极能量密度qa(r)

为[5]：

式中：Fa为正极能量分配系数；U、I分别为实测放电电压、电流值。

本文以I=20 A、U=20 V为仿真传热模型的电流值和电压值，该数值可由图2得到。

3 能量分配系数在传热模型中的确定

3.1 确立传热物理模型

COMSOL Multiphysics是一款大型高级数值仿真软件，广泛应用于各领域的科学研究及工程计算，被科学家称为“第一款真正的任意多物理场直接耦合分析软件”。模拟科学和工程领域的各种物理过程，COMSOL Multiphysics以高效的计算性能和杰出的多场双向直接耦合分析能力，实现了高度精确的数值仿真。对于水中电火花固体传热和流体传热的耦合模型，将COMSOL中的固体传热模型与流体传热模型相耦合，对工件材料的温度场进行分析。通过计算固体-流体传热耦合模型在水介质作用下的温度场分布，进而得到水中火花放电的电蚀坑形貌。

3.2 传热控制方程与设置边界条件

在仿真模拟水中电火花放电的过程中，分别利用固体传热和流体传热2种传热控制方程对其进行分析：

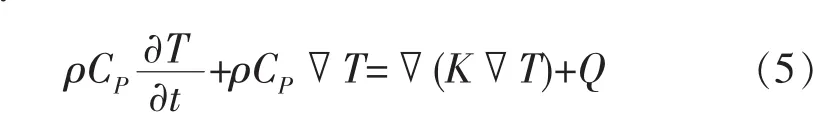
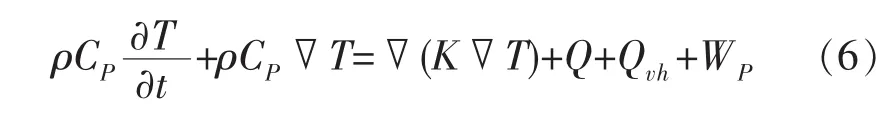
式中：ρ为固体密度；CP为常压热容；T为温度；t为时间；K为导热系数；Q为热量；Qvh为压力功；WP为对流传热。

当材料发生相变时，由于材料密度和传热系数都发生变化，从而影响了传热分布的准确性。因此，在固体传热和流体传热过程中，重新设定材料的热容CPE（即相变潜热），可更真实可靠地进行水中电火花加工的模拟分析：

式中：CPE为材料相变潜热。

4 仿真结果与模型验证

4.1 计算不同能量分配系数的电蚀坑直径

通过设定不同的能量分配系数，计算得到相应的电蚀坑直径。如计算得到的电蚀坑直径与实验测量值近似或误差较小时，则设定的正极能量分配系数即为水中电火花加工的能量分配系数。通过已建立的固体-流体传热物理模型，设定不同的正极能量分配系数，计算得到相应的电蚀坑直径（表3）。

表3 设定不同能量分配系数计算得到的电蚀坑直径μm

当设定的Fa与实际水中电火花加工的能量分配系数接近时，即根据固体-流体传热耦合模型计算得到的电蚀坑直径与实验测量值之间的误差率最小时，认为此时设定的能量分配系数即为实际的能量分配系数。由表3和图3可见，当正极能量分配系数Fa=0.23时，不同加工条件下计算得到的电蚀坑直径与实际测量值较接近。因此可说明，分析水中电火花加工所建立模型的正极能量分配系数为0.23。

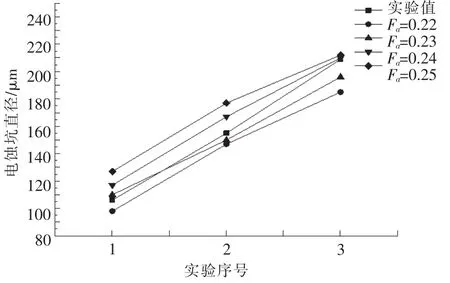
图3 不同能量分配系数对于的电蚀坑直径对比

4.2 验证模型的正确性

一般情况下，由于负极的能量分配系数极小，导致材料去除率也相当小，所以不适合进行加工。因此，本文仅对正极性加工的能量分配系数进行验证。通过对比计算得到的电蚀坑形貌与实验观察得到的电蚀坑形貌，可以验证所建立模型的正确性。当取正极能量分配系数为0.23时（图4、图5），通过实验得到的电蚀坑直径与仿真结果的相近度为96.77%。实验时的峰值电流为45 A，脉宽为20 μs。

此外，对比表3的计算结果与实验结果发现，通过式（1）所示的电蚀坑半径随放电脉宽和峰值电流的变化关系，结合固体-流体传热耦合模型分析得到的正极能量分配系数0.23的误差率在5%以内，说明所建立的模型是正确的。

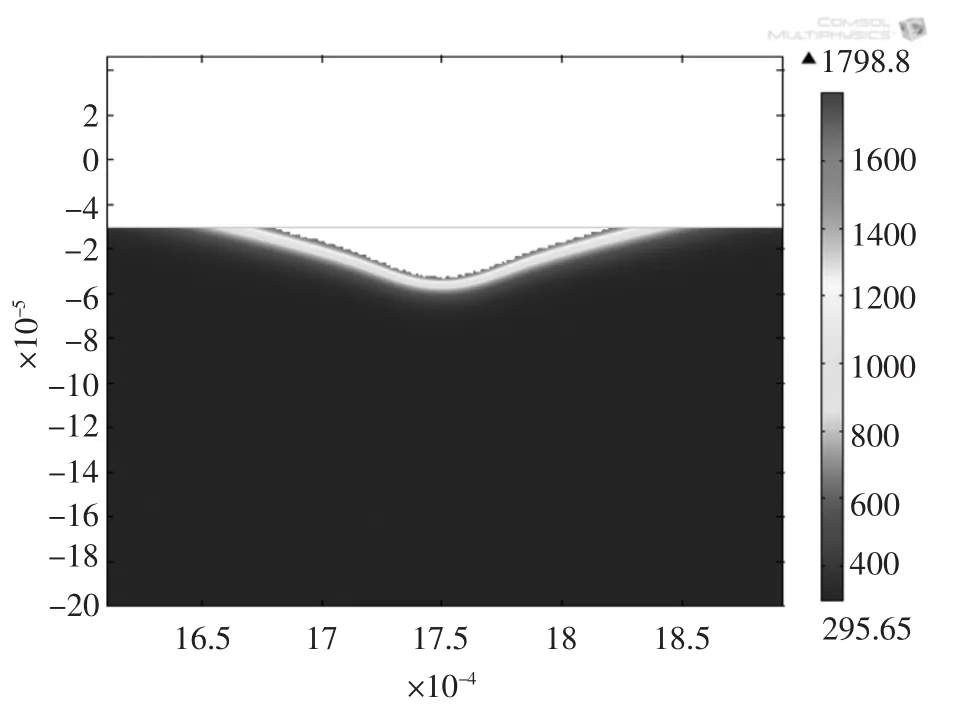
图4 通过仿真得到的电蚀坑直径

图5 通过实验得到的电蚀坑直径

图6 通过实验得到的电蚀坑深度

5 总结与展望

建立了水中电火花加工的固体-流体传热耦合模型。通过实验得到不同参数条件下的电蚀坑半径，并结合最小二乘法拟合电蚀坑半径随脉宽和电流的变化规律。通过仿真计算得到不同能量分配系数下相应参数的电蚀坑半径，并与实验测量值进行比对，得到水中电火花加工的能量分配系数为0.23。利用实验与仿真结果对比的方法，验证所建立固体-流体耦合模型的正确性，为今后水中电火花加工的机理研究提供重要依据。

通过对电火花加工机理的研究，能促进电火花加工技术的发展[6]。基于有限元仿真软件，建立相关模型，分析实际加工随时间及参数变化的过程是电火花加工理论研究的有效手段之一。虽然本文建立的流体-固体传热模型没有给出负极能量分配系数，但通过深入研究即可得到；同时，可不断解决模型中存在的问题，不断接近真实电火花加工的过程，以此推动电火花加工技术的进步。

[1] Xia Heng，Kunieda M，Nishiwaki N.Removal amount difference between anode and cathode in EDM process[J].IJEM，1996（1）：45-52.

[2] DiBitonto D D，Eubank P T，Patel M R，et al.Theoretical models of the electrical discharge machining process.I.A simple cathode erosion model[J].Journal of Applied Physics，1989，66（9）：4095-4103.

[3] Patel M R，Barrufet M A，Eubank P T，et al.Theoretical models of the electrical discharge machining process.II. The anode erosion model[J].Journal of Applied Physics，1989，66（9）：4104-4111.

[4] Ikai T，Hashigushi K.Heat input for crater formation in EDM [C]//Proceedings of International Symposium for Electro-machining，ISEM XI. Lausanne，Switzerland，1995：163-170.

[5] 薛荣，顾琳，杨凯，等.喷雾电火花铣削加工的能量分配与材料蚀除模型[J].机械工程学报，2012，48（21）：175-182.

[6] 许华宇，李明辉，彭颖红.电火花加工理论研究现状与展望[J].电加工与模具，1997（3）：8-12.

Research on Energy Distribution Coefficient of Electro-discharge in Water

Gao Ruiheng，Zhang Fawang，Gu Lin，Zhao Wansheng
（Shanghai Jiao Tong University，Shanghai 200240，China）

By the method combined experiment and simulation，designing different peak currents and pulse durations，energy distribution coefficient of EDM in water and the formation of electrodischarge crater morphology are studied.Based on COMSOL MULTIPHSICS simulation software，a solid-fluid coupling heat transfer model is established.Under the experiment with different peak currents and pulse durations，electro-discharge crater radius are obtained，and the relationship of electro-discharge crater radius between pulse duration and current are fitted.Using fitted formula and established model，the electro-discharge crater radius corresponded with thedifferentenergy distribution coefficients under different parameters are calculated.Comparing measuring values and calculated ones，the energy distribution coefficients of electro-discharge in water are oblained，and the model is verified.

electro-discharge in water；energy distribution coefficient；solid-fluid coupling heat transfer model

TG661

A

1009－279X（2014）02－0001-04

2013-10-30

国家自然科学基金资助项目（51175337）第一作者简介：高睿恒，男，1988年生，硕士研究生。