数值积分的迭代方法及应用

何俊俊，苏岐芳

（台州学院 数学与信息工程学院，浙江 临海 317000）

数值积分的迭代方法及应用

何俊俊，苏岐芳＊

（台州学院 数学与信息工程学院，浙江 临海 317000）

在工程和科学计算中，经常会遇到各种类型的积分问题.对于被积函数过于复杂，其原函数很难求得，甚至原函数根本就不是初等函数；或不知道被积函数的解析式，而只给出被积函数在有限个点处的函数值等情况，需要利用数值积分方法求积分的近似值．给出了两种逐次分半求积算法和二重积分的复合梯形算法，并利用这些方法解决了几类实际问题.

数值积分；算法；收敛速度；MATLAB程序

1 引言

数值积分在金融数学，计算机图形学，积分方程，工程计算等许多科学领域都有非常重要的应用，科学和工程计算中的许多实际问题最终也都会归结为数值积分的计算问题［1］.

由微积分定理，若被积函数f（x）在区间［a，b］上连续，只要能找到f（x）的一个原函数F（x），便可以利用牛顿-莱布尼茨公式求得积分值.然而，在实际应用中常常会碰到一些困难，导致不能用牛顿-莱布尼茨公式直接求得定积分的值．其中，可能出现的情况有［1-2］：

（1）某些函数，其原函数不能用初等函数表示；

（2）函数f（x）的结构复杂，其原函数很难求得；

（3）函数f（x）的表达式不明显，用表或图的功能，只给出苦干离散点上的函数值.

一般地，可根据给定的节点构造机械求积公式：

其中xk是求积节点；Ak是求积系数，也称伴随节点xk的权.

2 复合求积公式

通常把积分区间等分成若干子区间，在每个小区间上利用牛顿-柯特斯公式，再把每个小区间上的结果相加作为整个区间上的积分近似值．本文考虑逐次分半迭代方法．

2.1 梯形递推公式

将积分区间［a，b］分为n等份，则有复合梯形公式：

将每个小区间再次二等分后，得梯形递推公式［2，8］

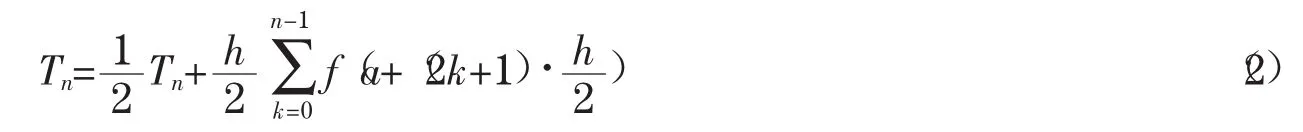
2.2 辛普森递推公式

将积分区间［a，b］分为n等份，则有复合辛普森公式：

将每个小区间再次二等分后，

即得辛普森递推公式

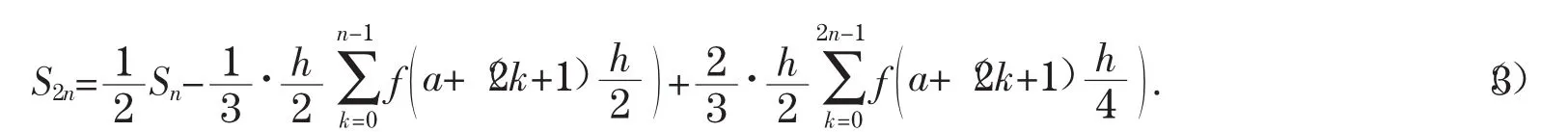
2.3 二重积分求积公式

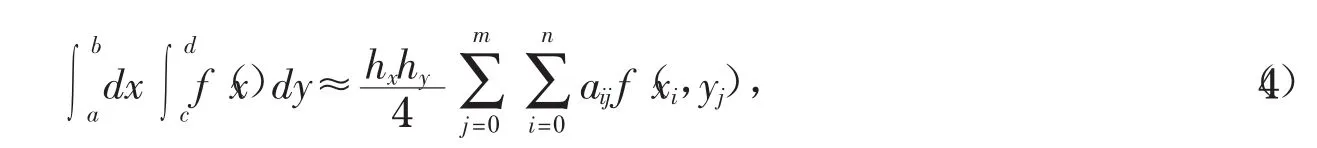
其中aij是下面矩阵A的对应元素：

3 求积迭代算法

算法1：逐次分半梯形法

（1）取k=0，h=b-a，计算T1；

（2）计算第一次分半梯形值T2；

（3）计算误差err=T2-T1；

（4）如果err＜ε（预先给定的精度），则停止；否则令k+1→k，T2→T1；

（5）计算T2k，并令T2k→T2转步骤（3）．

算法2：逐次分半辛普森法

（1）取k=0，h=b-a计算S1；

（2）计算第一次分半辛普森值S2；

（3）计算误差err=S2-S1；

（4）如果err＜ε（预先给定的精度），则停止；否则令k+1→k，S2→S1；

（5）计算S2k，并令S2k→S2转步骤（3）．

4 数值积分的应用

4.1 卫星轨道问题

我国第一颗人造卫星近地点距离h=439km，远地点距离H=2384km，地球卫星轨道是一个椭圆，试求卫星轨道的周长（地球半径为R=6371km），且轨道周长公式为

由问题可知，轨道的周长与卫星轨道的半轴长a以及地球中心与轨道中心（椭圆中心）的距离c有关，地球半径为R=6371km，因而a，c可由近地点、远地点、地球半径求出：

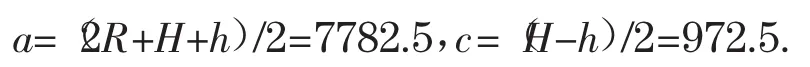
在MATLAB-R2011a环境下，分别用逐次分半梯形法、逐次分半辛普森法和龙贝格算法［2，8］求轨道周长的近似值，要求误差小于5×10-8，并比较各种算法所需分半次数及所需CPU时间．运行结果如表1．

表1 三种算法的计算结果Table.1 Te results of three algorithm

由输出结果看到，对于给定的数据，三种算法收敛速度都很快，所需CPU时间基本相同．

4.2 男大学生身高问题

据资料报道,中国大学生男子组的平均身高是170cm，高度在150cm组至190cm组之间的人大致有99.7%．若是把［150cm，190cm］平均分成20个高度区间，那男子组身高在每一高度区间的分布情况如何呢？并且，你能求出身高中等（165cm至175cm之间）的人占男子组的百分比会超过60%吗？

由问题可知，身高受很多因素影响，通常它是一个服从正态分布N（u，σ）的随机变量。正态分布的概率密度函数φ（x）为：

则密度函数φ（x）在区间［a，b］上的定积分的值能够较好的代表大学生男子组的身高在区间［acm，bcm］的分布，在密度函数φ（x）中的两个参数μ、σ分别是正态分布中的均值与标准差.

据了解，中国大学生男子组的平均身高是170cm，那么正态分布选取的均值u=170cm，而“该男子组中约有99.7%的人身高在150cm组至190cm组之间”符合了正态分布N（u，σ）的“3σ规则”的条件，即P （μ-3σ＜x≤μ+3σ）=99.7%，得到

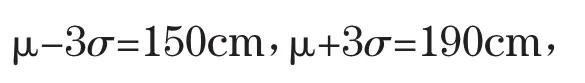
将［150cm，190cm］等分成20个高度小区间，即

在各个小区间内的身高分布情况对应于积分值

身高在165cm至175cm之间的人占该男子组的百分比为

即身高中等的人占男子组的百分比．

身高分布函数φ（x）的图像如图1．现用数值积分方法求积分（8）的近似值，要求误差小于10-4．

（1）逐次分半梯形法计算结果，见表2.

表2 逐次分半梯形法计算结果Table.2 Results by using composite trapezoidal formula

其中n为分半次数．由（9）式计算得

即身高中等（165cm，175cm）的大学生约为54.67%，不足60%．梯形求积公式计算结果的分布曲线见图2．

（2）逐次分半辛普森算法计算结果，见表3.

表3 逐次分半辛普森算法计算结果Table.3 Results by using composite Simpson’s formula

由（9）式计算得

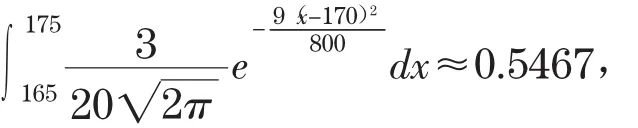
即身高中等（165cm，175cm）的大学生约为54.67%，不足60%．辛普森求积公式计算结果的分布曲线见图3。

图1 被积函数φ（x）的分布Fig.1 Distribution of the integrand

图2 逐次分半梯形算法结果的分布Fig.2 Distribution of trapezoidal integration

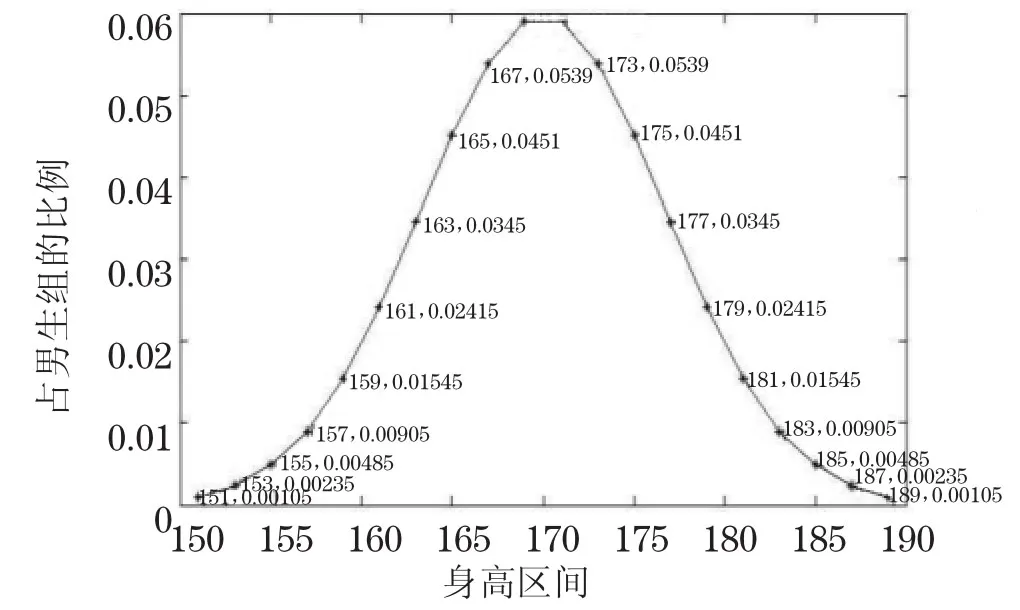
图3 逐次分半辛普森算法结果的分布Fig.3 Distribution of Simpson’s integration

图4 三种算法的结果比较Fig.4 Comparison of three methods

将密度函数φ（x）的曲线、逐次分半梯形法计算结果的曲线、逐次分半辛普森法计算结果的曲线画在同一坐标系下得比较图，即图4.由分布曲线可知，逐次分半梯形求积公式、逐次分半辛普森求积公计算结果基本符合正态分布，且分布曲线与标准分布曲线φ（x）拟合得很好.由表2和表3也可以看出，逐次分半辛普森公式收敛速度较快.

4.3 储量计算问题

某地区为了估计某种矿物的储量，考察队来到该区进行勘测，得到如下数据（见表4）.请估计出此地区内（1≤X≤4，1≤Y≤5）该矿物的储量.

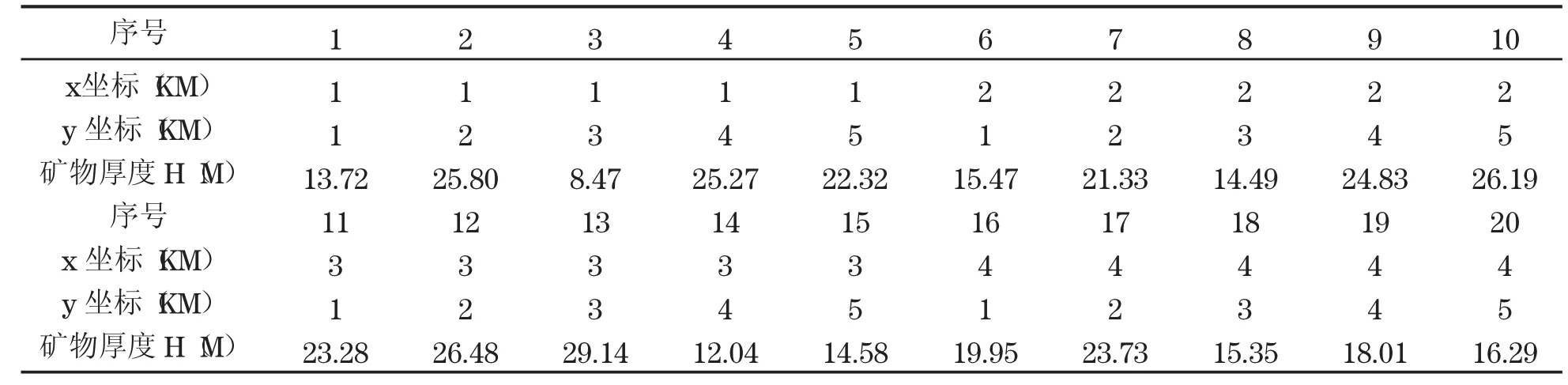
表4 地区勘探数据表Table.4 regional exploration data

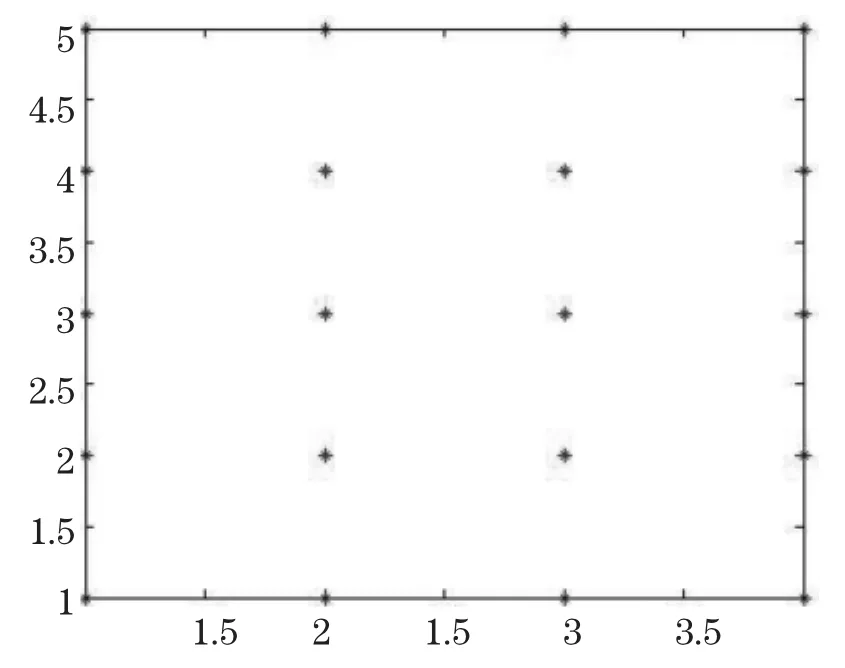
图5 数据点位置示意图Fig.5 Locations of the data points

图6 矿物的储量分布Fig.6 Distribution of mineral reserves

利用公式（4）和（5），其中hx=hy=1，n=3，m=4，相应的矩阵

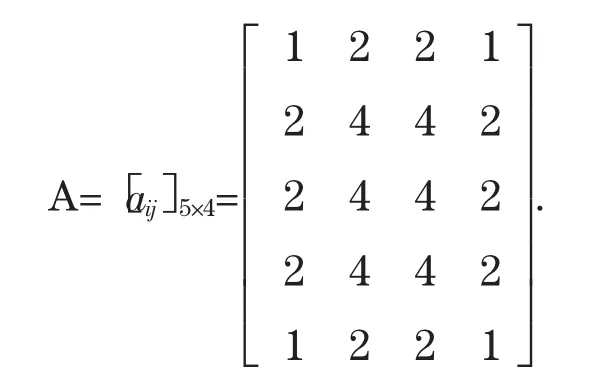
经计算，结果为256.320．统一单位后，得到该矿物的储量约为2.56320×108（立方米），矿物储量拟合图见图6.

由于给定的节点关于横坐标x是奇数等分的分点，所以选用二重复合梯形求积公式计算较为合理．如果节点关于横坐标x和纵坐标y都是偶数等分的分点，则也可以用二重复合辛普森求积公式计算.

5 结论

通过对上述三个实际问题的求解，不难发现，对于只给出有限个节点及其函数值的积分问题，针对不同的数据应采用不同的分析、求解方法．一般情况下，逐次分半辛普森法的收敛速度是比较快的，甚至有时与龙贝格算法所需分半次数一样.对于二重数值积分问题，如果被积函数的解析表达式未知，可利用复化梯形公式求积分的近似值.

［1］徐利治.数值积分法研究近况综述［J］.数学进展，1982,11（2）：135-143.

［2］李庆扬等.《数值分析》第五版［M］.北京：清华大学出版社，2008.12：97-102

［3］王少英.数值积分若干方法的比较分析［J］.2012,28（6）：14-18.

［4］张智丰.《数学实验》［M］.北京：科学出版社，2008.

［5］NENAD UJEVIC.Double integral inequalities and application in numerical integration［J］.Periodica Mathematica Hungarica,2004,49（1）：141-149.

［6］董志远等.二重数值积分的计算方法的比较［J］.太原师范学院学报（自然科学版），2009,8（4）：20-23.

［7］AVRAM SIDI.Extension of a class of periodizing variablerans formationst for numerical integration［J］MATHEMATICS OF COMPUTATION,2005,75（253）：327-343.

［8］苏岐芳等.《数值分析》［M］.北京：中国铁道出版社，2007.

Iterative Methods of Numerical Integration and its Applications

HE Jun-jun，SU Qi-fang＊

（School of Mathematics and Information Engineering,Taizhou university,Linhai 317000,China）

We often encounter various types of integration problems in engineering and scientific computation.The integrand is too complex, even not the elementary function; or the analytical formula of the integrand is unknown.Only some nodes are given.There is a need to solve the approximation of integration.In this paper,we give two iterative algorithms of numerical integration and composite trapezoidal role for double integration, and solve some practical problems by using these iterative methods.

Numerical integration;algorithm;convergence speed；MATLAB program

10.13853/j.cnki.issn.1672-3708.2014.03.001

2014-05-05；

2014-05-20

简介：苏岐芳（1964- ），女，黑龙江绥化人，副教授，硕士，主要从事计算数学与应用数学的教学与研究。