分析课程中若干重要概念与定理的教学探究

虞志坚

（台州学院 数学与信息工程学院，浙江 临海 317000）

分析课程中若干重要概念与定理的教学探究

虞志坚

（台州学院 数学与信息工程学院，浙江 临海 317000）

对分析课程中导数与微分概念以及鲁津定理与富比尼定理的教学作了若干探究。首先，我们强调要将一元函数、多元函数以及向量值函数的导数和微分纳入统一的框架之中进行教学。其次，对于鲁津定理我们要突出定理的关键是用连续函数逼近可测函数时不能破坏函数总体性质。最后，关于富比尼定理我们指出定理的重点是先判断被积函数的可积性。

导数；微分；鲁津定理；富比尼定理；教学探究

微积分、数学分析、实变函数等分析课程是地方高校数学课程中十分重要的组成部分。对于这些课程中重要概念与定理的教学，无疑是值得探究的。任课教师通过自己的教学研究和实践，明确教学这些重要概念与定理的关键所在，并在教学实践中突出强调它们，才能使学生尽快理解并掌握这些重要的概念和定理，取得良好的课堂教学效果。本人从事微积分与实变函数的课程教学多年，积累了一定的教学经验。下面我们从微积分和数学分析中的导数与微分概念，以及实变函数中的鲁津定理与富比尼定理出发，对这些概念与定理的教学做一些探究。

1 关于导数与微分

导数与微分是微积分和数学分析中两个最基本也是非常重要的概念。我们觉得不论是一元函数、多元函数，还是由多个函数组成的函数，对于有关它们的导数与微分的教学，应当纳入统一的框架之中，才能从更高的层次上理解并掌握它们。

我们知道，当函数y=y（x）在x点可微时，其增量△y=y（x+△x）-y（x）的线性主部，即y（x）在x点的微分可以表示为A△x，其中线性映射A：就是函数y=y（x）在x点的导数，它只与x有关而与△x无关［1］。

若二元函数y=y（x1，x2）在点（x1，x2）可微，则其全增量的线性主部，即y=y（x1，x2）在点（x1，x2）的全微分可以表示为

其中线性映射A1，A2：分别是函数y=y（x1，x2）在点（x1，x2）处关于x1与x2的偏导数，它们与△x1，△x2无关而仅与x1，x2有关［2］。这里行向量）可以看作是函数y=y（x1，x2）在点（x1，x2）处的

“导数”。

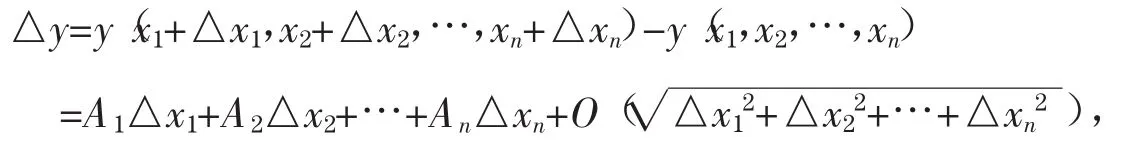
且其中A1，A2，…，An与△x1，△x2，…，xn无关而仅与x1，x2，…，xn有关，则称函数y=y（x1，x2，…，xn）在点（x1，x2，…，xn）可微，并称全增量△y的线性主部

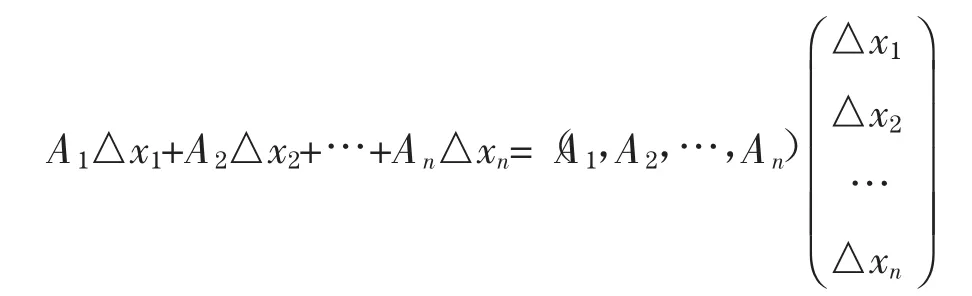
为函数y（x1，x2，…，xn）在点（x1，x2，…，xn）的全微分。其中A1，A2，…，An：Rn→R1都是线性映射，它们是y=y （x1，x2，…，xn）关于在点（x1，x2，…，xn）处关于x1，x2，…，xn的所有一阶偏导数。这里行向量（A1，A2，…，An）=）可以看作是函数y=y（x1，x2，…，xn）在点（x1，x2，…，xn）处的“导数”.

综上，函数的微分都是其增量的线性主部。对于一元函数，其导数就是通常的一阶导数；而对于多元函数，其导数是由该函数所有一阶偏导数构成的行向量。

若函数Y（x1，x2，…，xn）的增量可以表示为如下形式：

且其中A11，A12，…，Amn与△x1，△x2，…，△xn无关而仅与x1，x2，…，xn有关，则称函数Y=Y（x1，x2，…，xn）在点（x1，x2，…，xn）“可微”，并称

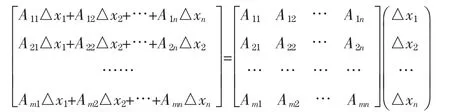
为函数Y（x1，x2，…，xn）在点（x1，x2，…，xn）处的“微分”。其中都是线性映射，它们是y1（x1，x2，…，xn），y2（x1，x2，…，xn），…，ym（x1，x2，…，xn）在点（x1，x2，…，xn）处关于x1，x2，…，xn的所有一阶偏导数。这里m×n矩阵

可以看作是函数y=y（x1，x2，…，xn）在点（x1，x2，…，xn）处的“导数”，它就是著名的雅可比矩阵。因此，对于由多个函数组成的函数，其微分和导数是单个函数的微分和导数的更一般的形式，即从低维向高维的推广。

最后，对于无限维空间，我们同样可以引入“微分”与“导数”的概念，方法类似。这种情形下，“导数”则是更一般的连续线性算子。

对于非数学系的学生，在讲授了一元函数的导数与微分，以及多元函数的偏导数与全微分后，就可以将一元函数与多元函数的导数与微分统一到同一框架下了。而对于数学系的学生，在讲授了向量值函数导数与微分后，又可进一步将一元函数、多元函数以及向量值函数的导数与微分纳入到同一框架，更进一步可以向学生介绍在无限维空间中也可以用类似的方法引入导数与微分。进而强调这些导数与微分概念都是可以纳入同一框架下统一处理的。那样就可以在更高的层次上理解导数与微分这两个概念从而尽快掌握它们。所以，对于导数和微分这两个最基本但却非常重要的概念，我们要强调的是同一框架统一处理。这样能在更高的层次上理解导数与微分这两个最基本的概念。

2 关于鲁津定理

在实变函数中，可测函数的构造是很重要的内容，我们以直线上的鲁津定理为例：

定理［3］：设f（x）是可测集上的几乎处处有限的可测函数，则对任意δ＞0，存在闭集F∪E以及整个上的连续函数g（x），使得在F上g（x）=f（x），且m（EF）＜δ.

鲁津定理是关于可测函数用连续函数逼近的问题。用已知的函数来逼近新引入的函数如可测函数，是常用的方法。但是，用什么函数，以何种方式逼近却是关键所在。连续函数是我们熟知的一类有着良好性质的函数，考虑用连续函数逼近可测函数是很好的思路。然而更重要的是用怎样的方式逼近可测函数。鲁津定理告诉我们可以在不破坏函数总体的条件下用连续函数逼近可测函数。这是我们在教学的时候要特别强调的！它是数学家鲁津在对可测函数有了深刻洞察后得到的结果，普通人没有他那样的水平。

3 关于富比尼定理

以数学家圭多·富比尼命名的富比尼定理，是分析中关于重积分的一个重要定理：

定理［4］：（1）设函数f（x，y）是（其中A，B分别是中的可测集）上的可测函数。若

其中积分是关于乘积空间A×B上乘积测度的积分，则

其中第一个积分是关于乘积空间A×B上乘积测度的积分，后两个是在两个测度空间上积分的迭代。

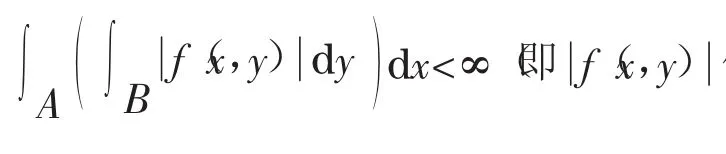
富比尼定理给出了使用逐次积分的方法计算二重积分的条件。在这些条件下，不仅能够用逐次积分计算二重积分，而且交换逐次积分的顺序时，积分结果不变。

在富比尼定理教学中不能仅限于对富比尼定理的文字叙述，需要特别强调的是：富比尼定理的关键在于判断是否可积，然后才是计算积分！而这恰恰是教学中容易被忽略的。因为可测函数的可积性与绝对可积性是等价的，所以要先判断被积函数加了绝对之后是否可积（计算或估计），然后再运用富比尼定理计算积分。之所以要先对添了绝对值后的被积函数进行可积性判断，是因为通常情况下，不加绝对值的被积函数很难判断它是否可积甚至无法判断其可积性！

综上所述，对于导数与微分，我们要强调同一框架统一处理；对于鲁津定理，我们强调定理的关键是逼近可测函数时不破坏函数的总体；对于富比尼定理，我们要强调定理的关键在于先判断是否可积。我们认为这样可以使学生能尽快理解并掌握这些概念与定理，从而取得良好的教学效果。

［1］陈传璋,金福临,朱学炎,等.数学分析（上册）［M］.北京：高等教育出版社，1983：148-149．

［2］陈传璋,金福临,朱学炎,等.数学分析（下册）［M］.北京：高等教育出版社，1983：144-145．

［3］程其襄,张奠宙,魏国强等.实变函数与泛函分析基础［M］.北京：高等教育出版社，2010：88．

［4］程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础［M］.北京：高等教育出版社，2010：130．

Teaching Explorations on Some Important Concepts and Theorems in Analysis

YU Zhi-jian

（School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China）

In this note,some teaching explorations on important concepts and theorems in analysis are done.Firstly, concerning the derivatives and differentials of single or several variable functions and vector-valuedfunctions,it is important that we should teach them in the same frame.Secondly,as for Lusin’s theorem it should be emphasized that we must keep the global properties of a measurable function when we use a continuous one to approximate it.Lastly,it must be pointed out that the key of Fubini’s theorem is that we have to check the integrability of the integrands first.

Derivatives;Differentials;Lusin’s Theorem;Fubini’s Theorem;Teaching Explorations

10.13853/j.cnki.issn.1672-3708.2014.03.014

2014-04-02；

2014-05-12

虞志坚（1971- ），男，浙江台州人，副教授。