基于Hilbert-Huang变换识别柴油机缸盖阻尼比

李晓磊，刘建敏，李晓伟，乔新勇

（1.装甲兵工程学院机械工程系，北京 100072；2.解放军77160部队，四川犍为 614400；3.中国水利水电第十四工程局有限公司机电安装分公司，云南昆明 650032）

阻尼比是研究机械振动时不可或缺的参数，它反映了激励源振动响应的衰减过程。阻尼比往往通过试验得到。对于试验数据常用的处理方法可分为频域法和时域法。其中频域法需要测量完整的输入和输出信号，试验过程比较繁琐，处理算法主要有半功率带宽法、频率细化法等；时域法通常针对单自由度线性系统的自由衰减信号进行分析，具体方法有对数衰减率法、随机减量法等[1]。近年来针对工程结构的健康监测与损伤识别，国内外学者提出了基于 Hilbert-Huang变换（Hilbert-Huang Transform，HHT）的模态参数识别法，取得了较好的效果[2―5]。该方法利用经验模式分解（Empirical Mode Decomposition，简称EMD）将某一测点的自由振动信号分解为多个模态响应衰减信号，再通过希尔伯特变换（HT）和最小二乘拟合求解每个模态响应的频率和阻尼比。本文应用该方法对柴油机缸盖的阻尼比进行了计算，得到的模态频率及阻尼比在合理范围之内，将该参数应用于缸盖的瞬态动力学计算，取得了较好的效果。

1 HHT的基本理论

HHT主要有两个步骤：首先对多分量信号进行EMD分解，得到单分量信号；其次对每个单分量信号做Hilbert变换（HT），得到每个分量的瞬时频率和幅值。

1.1 EMD分解

EMD分解的思想就是将信号分解成为若干个相对平稳的、互不相关的本征模态函数（IMF）。

一个本征模态函数应满足下面2个条件[6，7]：

1)整个数据序列中，极值点的数量与过零点的数量应相等，或最多相差一个。

2）在任一时间点上，信号的局部极大值和局部极小值定义的局部均值应该为零。

EMD方法首先要找出信号x(t)的局部极值，再通过插值方式求出上下包络线；计算上下包络线的均值，记作m1；通过式(1)计算

重复上述步骤，直到得到的h1k满足本征模态数的条件，即认为h1k为第1个本征模态函数。记：c1=h1k如此计算下去，最终获得信号的所有本征态函数cn和残余分量rn，原始信号即可表示为

1.2 Hilbert变换（HT）

HT变换重要应用价值在于提供了描述信号瞬时变化特征的手段，因而适合于处理非线性及非平稳等具有明显瞬时变化特征的信号。为了使瞬时频率的定义有物理意义，HT变换只能应用于单一成分的信号，对于频率成分复杂的多分量信号，EMD分解可以解决这一难题[8，9]。针对每个单分量的信号ci作HT变换

2 HHT模态参数识别的基本流程

单自由度线性系统自由振动响应[10]

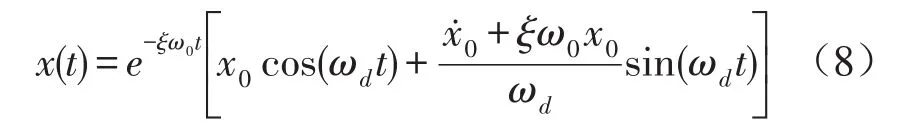
结合4式可得x(t)的解析信号为

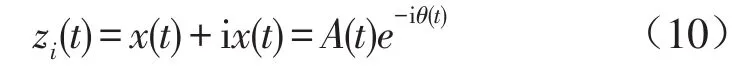
对于阻尼较小，频率相对较高的系统，上式中的幅值及相位可进一步表示为

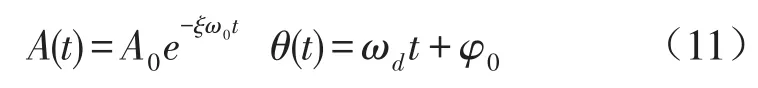
对幅值及相位分别引入对数及微分算子，可得

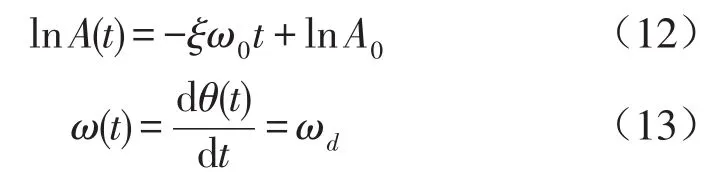
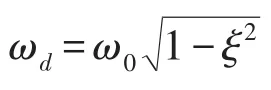
对于线性多自由度系统的自由振动，先确定信号的频率分布情况，利用带通滤波和EMD相结合的方式提取各频率成分对应的态响应，再利用上述方法识别固有频率及阻尼比。具体流程如图所示。

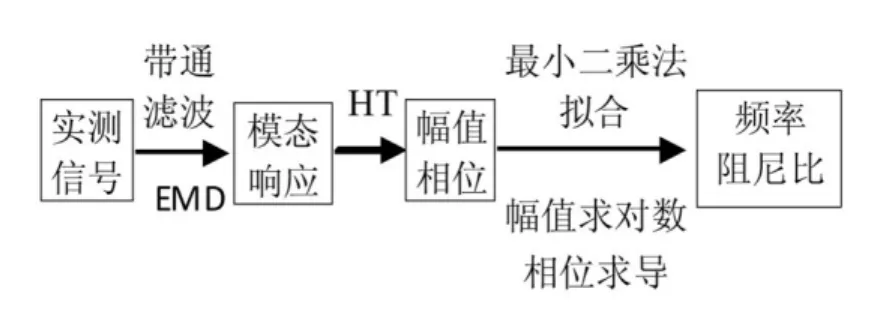
图1 基于HHT识别模态参数的流程图

3 振动检测试验

针对某型12150柴油机进行缸盖敲击振动检测试验，测试设备如图2所示，主要包括检测平台，传感器以及移动电源等。检测时选用振动加速度传感器，激励采用锤击方式。实测的振动加速度信号如图3所示，信号呈现明显的自由衰减趋势，反映了结构阻尼特性对能量的衰减过程。

4 基于HHT的缸盖阻尼比识别

对实测振动加速度信号作功率谱。如图4所示，在500～8 000 Hz之间分布着很多特征频率，但有相当数量的频率能量较弱，由于试验中的采样误差、噪声污染等因素的影响，准确识别这些模态参数尤其是阻尼比是比较困难的，因此本文主要选择能量较大特征频率进行系统参数的识别，分别是1 230 Hz，1 624 Hz，2 750 Hz，7 263 Hz。

图2 振动检测设备

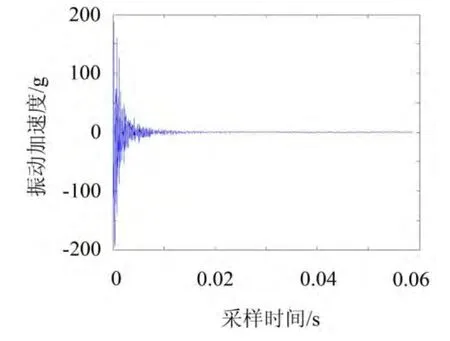
图3 实测振动加速度

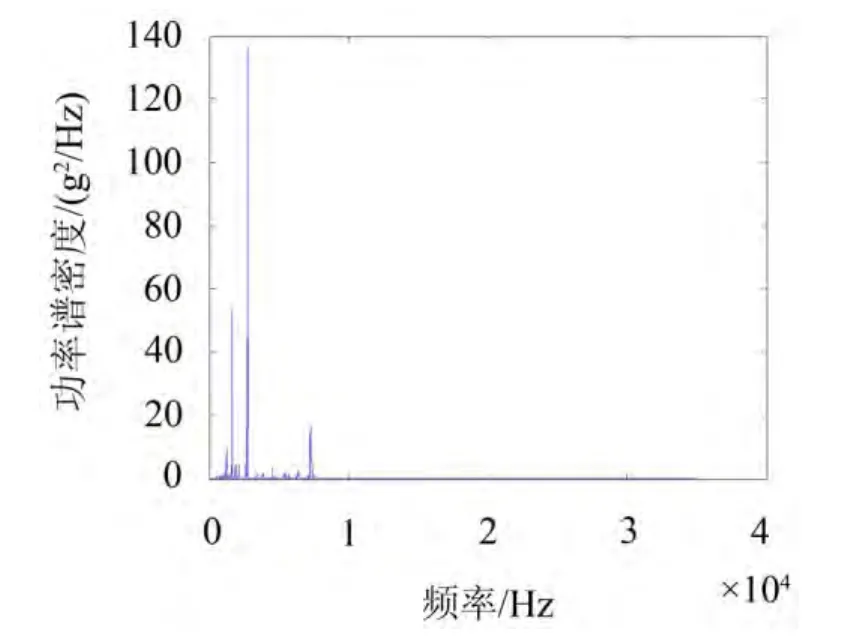
图4 功率谱密度

针对各特征频率分别选用1 225～1 235，1 620～1 628 Hz，2 745～2 755 Hz，7 258～7 268的带通滤波处理原始信号，将得到的信号进行EMD分解，各取第一个IMF分量作为各阶的模态响应。鉴于篇幅有限，文中仅列出1 230特征频率求解过程。由于带通滤波的影响，数据前段出现了信号幅值的放大，后段则由于噪声的影响出现了波动，如图5所示。为此，在计算瞬时幅值和瞬时频率时，取模态数据的第一个衰减段作为研究对象，如图6所示。

利用HT计算瞬时幅值和瞬时频率，并通过最小二乘法拟合瞬时幅值的对数，如图7所示。瞬时频率如图8所示，取平稳段的幅值作为最终瞬时频率值。

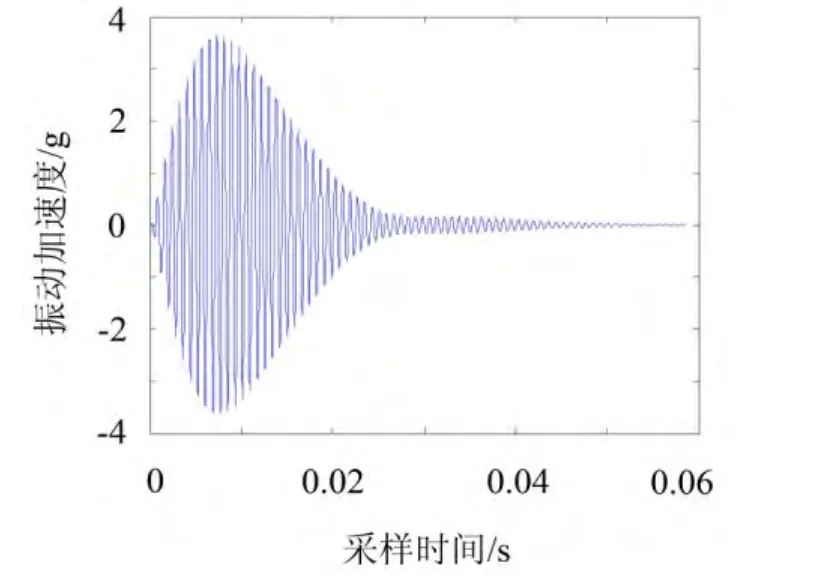
图5 1 230 Hz模态响应

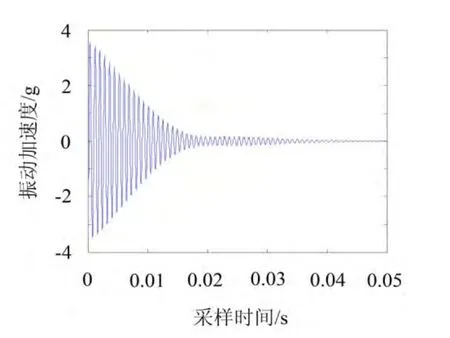
图6 1 230 Hz模态响应截取

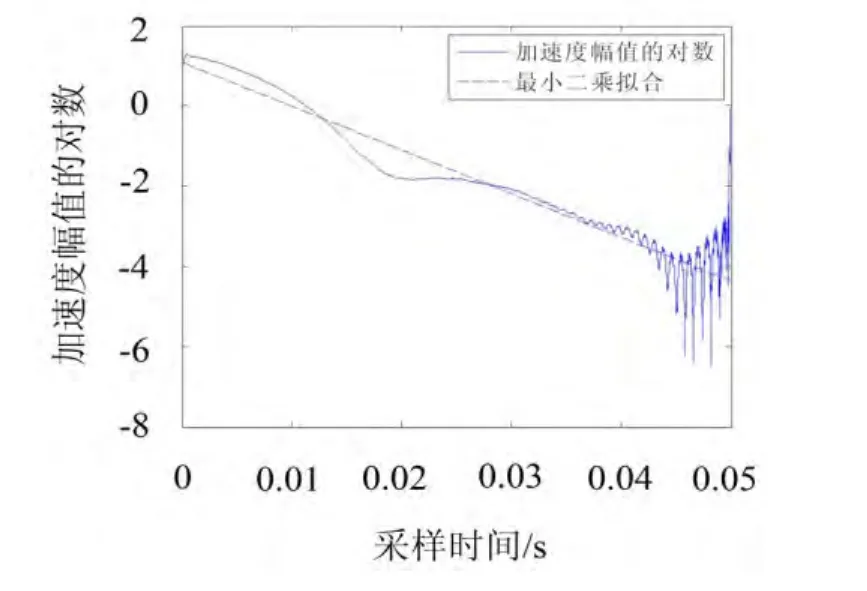
图7 1 230 Hz瞬时幅值的对数及其最小二乘拟合

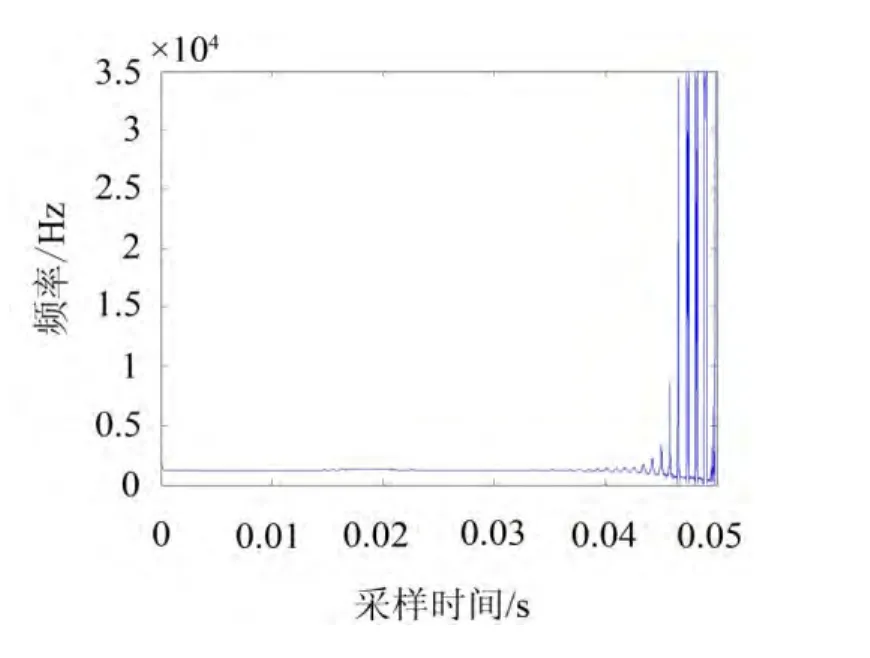
图8 1 230 Hz瞬时频率

图9 振动加速度对比

表1为最终得到的模态频率及阻尼比，不难看出，由于缸盖刚度大，阻尼比也较大，从模态分析考虑，符合一般的设计要求，这也间接说明该方法计算的模态频率及阻尼比值符合实际。

表1 模态频率及阻尼比

将以上参数用于缸盖系统的瞬态动力学仿真，研究缸内燃烧激励的振动响应。经过加载缸内压力载荷，设置边界条件，得到缸盖某一测点的振动加速度信号，如图9虚线所示，其中实线为同一测点的实测振动加速信号，由于实测结果中包含有其它激励源的干扰，如针阀落座激励以及活塞敲击激励，而仿真值仅考虑了燃烧激励的作用，导致二者在幅值和相位上存在一定偏差，但在上止点附近的变化趋势较为接近，说明计算得到的模态参数与阻尼比基本合理，能够满足缸盖系统动力学研究的需要。

5 结语

利用HHT算法处理缸盖振动衰减信号得到了缸盖系统的模态频率及阻尼比。

（1）由于缸盖设计刚度大，导致阻尼较大，初步认为计算模态参数符合实际情况。将其应用到缸盖系统的瞬态动力学仿真中，发现仿真结果与实测信号趋势相近，进一步验证了计算模态参数的合理性；

（2）相比传统的模态参数识别方法，HHT算法概念简单，且仅需一个测点的振动信号，试验过程较为简便，实用性更强。

[1]王慧，刘正士.一种识别结构模态阻尼比的方法[J]农业机械学报，2008，39（6），201-203.

[2]任宜春，易伟建，谢献忠.基于Hilbert-Huang变换的钢筋混凝土框架结构识别[J].振动与冲击，2007，26（2）：56-60.

[3]陈隽，徐幼麟，李杰.Hilbert-Huang变换在密频结构阻尼识别中的应用[J].地震工程与工程振动，2003，23（4）：34-40

[4]何旭辉，余志武，陈政清.基于EMD和随机减量技术的大型桥梁模态参数识别[J]铁道科学与工程学报，2007，4（4）：6-10.

[5]韩建平，李林，王洪涛，钱炯.基于Hilbert-Huang变换和随机减量技术的模态参数识别[J].世界地震工程，2011，27（1）：72-77.

[6]杨晓红，杨晓静，朱霄珣.基于EMD的支持向量回归机振动数据挖掘[J].煤矿机械，2010，31（11）：252-254.

[7]郭喜平，王立东.经验模态分解(EMD)新算法及应用[J].噪声与振动控制，2008，5：70-72.

[8]于德介，程军圣，杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京：科学出版社，2006.32-33.

[9]符娆，张群岩，赵述元.航空发动机试飞中转静子碰摩故障信号处理的希尔伯特－黄变换(HHT)方法[J].噪声与振动控制，2012，2：113-117.

[10]Jiping Lu,James J Little.Reflectance and shape from imagesusingacollinearlightsource[J].International Journal of Computer Vision,1999,32(3):213-240.